third lecture Parameter estimation maximum likelihood and least

third lecture Parameter estimation, maximum likelihood and least squares techniques Jorge Andre Swieca School Campos do Jordão, January, 2003

References • Statistics, A guide to the Use of Statistical Methods in the Physical Sciences, R. Barlow, J. Wiley & Sons, 1989; • Statistical Data Analysis, G. Cowan, Oxford, 1998 • Particle Data Group (PDG) Review of Particle Physics, 2002 electronic edition. • Data Analysis, Statistical and Computational Methods for Scientists and Engineers, S. Brandt, Third Edition, Springer, 1999

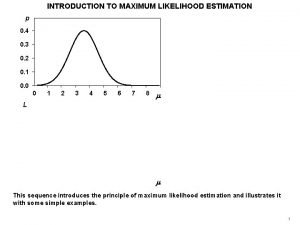
Likelihood “A verossimilhança (…) é muita vez toda a verdade. ” Conclusão de Bento – Machado de Assis “Quem quer que a ouvisse, aceitaria tudo por verdade, tal era a nota sincera, a meiguice dos termos e a verossimilhança dos pormenores” Quincas Borba – Machado de Assis

Parameter estimation p. d. f. f(x): sample space all possible values of x. Sample of size n: independent obsv. Joint p. d. f. Central problem of statistics: from n measurements of x , infer properties of , . A statistic: a function of the observed . To estimate prop. of p. d. f. (mean, variance, …): estimador. Estimador para : Estimador consistent (large sample or assimptotic limit)

Parameter estimation random variable distributed as (sampling distribution) Bias Infinite number of similar experiments of size n • sample size • functional form of estimator • true properties of p. d. f. b=0 independent of n: θ is unbiased Important to combine results of two or more experiments.

Parameter estimation mean square error Classical statistics: no unique method for building estimators given an estimator one can evaluate its properties sample mean From Estimator for E[x]=µ one possibility: supposed from unknown pdf (population mean)

Parameter estimation Important property: weak law of large numbers If V(x) exists, n→∞, is a consistent estimator for µ →µ in the sense of probability is an unbiased estimator for the population mean µ

Parameter estimation Sample variance s 2 is an unbiased estimator for V[x] if µ is known S 2 is an unbiased estimator for σ2.

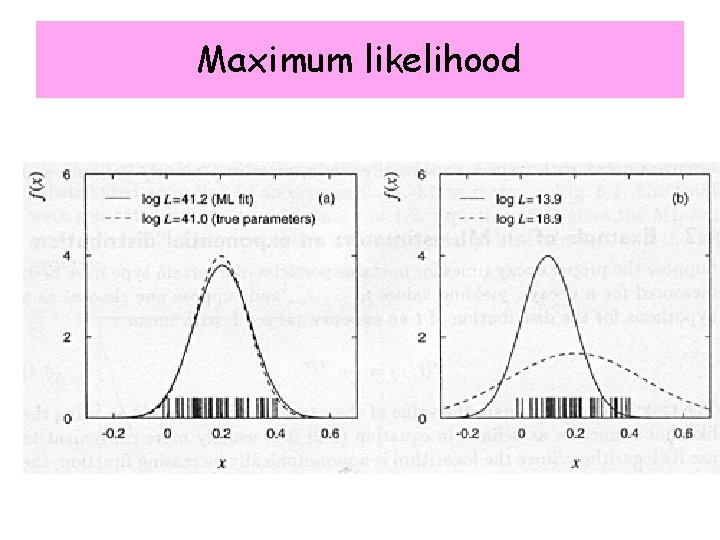
Maximum likelihood Technique for estimating parameters given a finite sample of data Suppose the functional form of f(x; θ) known. The probability of be in is prob. xi in for all i = If parameters correct: high probability for the data. likelihood function • joint probability • θ variables • X parameters ML estimators for θ: maximize the likelihood function

Maximum likelihood

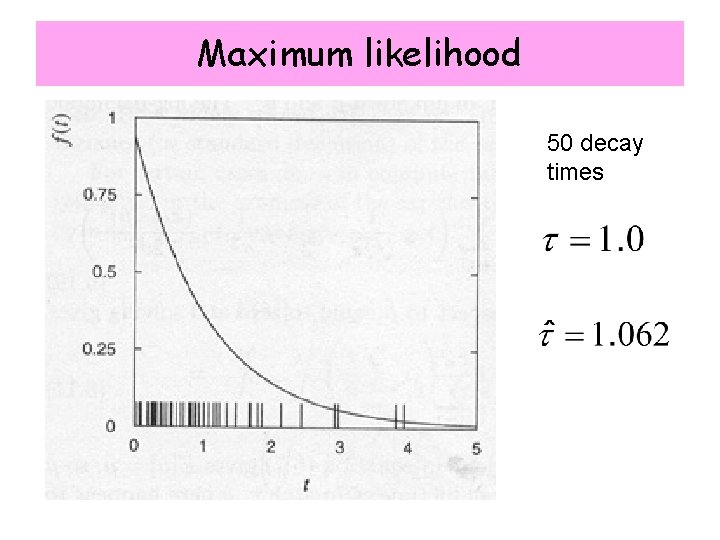
Maximum likelihood n decay times for unstable particles t 1, …, tn hypothesis: distribution an exponential p. d. f. with mean

Maximum likelihood 50 decay times

Maximum likelihood ? given unbiased estimator for when n→∞

Maximum likelihood n measurements of x assumed to come from a gaussian unbiased for large n

Maximum likelihood we showed that s 2 is an unbiased estimator for the variance of any p. d. f. , so is unbiased estimator for

Maximum likelihood Variance of ML estimators many experiments (same n): spread of analytically (exponential) transf. invariance of ML estimators ML estimate of ?

Maximum likelihood If the experiment repeated many times (with the same n) the standard deviation of the estimation 0. 43. • one possible interpretation • not the standard when the distribution is not gaussian (68% confidence interval, +- standard deviation if the p. d. f. for the estimator is gaussian) • in the large sample limit, ML estimates are distributed according to a gaussian p. d. f. • two procedures lead to the same result

Maximum likelihood Variance: MC method cases too difficult to solve analytically: MC method • simulate a large number of experiments • compute the ML estimate each time • distribution of the resulting values S 2 unbiased estimator for the variance of a p. d. f. S from MC experiments: statistical errors of the parameter estimated from real measurement asymptotic normality: general property of ML estimators for large samples.

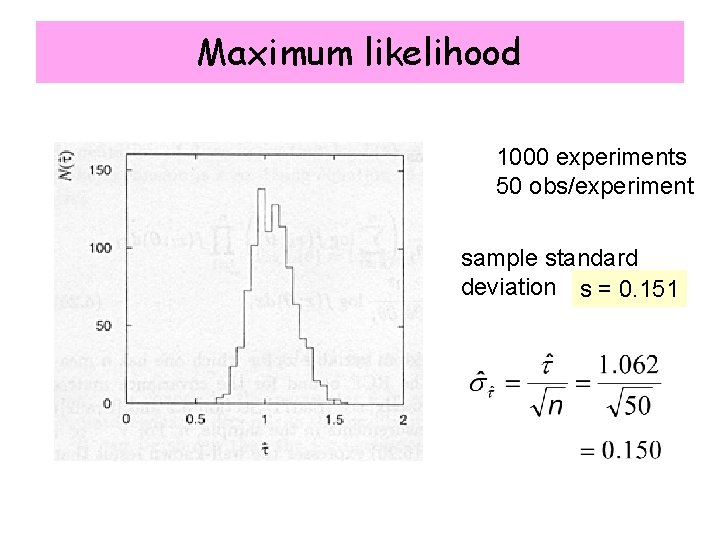
Maximum likelihood 1000 experiments 50 obs/experiment sample standard deviation s = 0. 151

RCF bound A way to estimate the variance of any estimators without analytical calculations or MC. Rao-Cramer-Frechet Equality (minimum variance): estimator efficient If efficient estimators exist for a problem, the ML will find them. ML estimators: always efficient in the large sample limit. Ex: exponential equal to exact result efficient estimator

RCF bound assume efficiency and zero bias statistical errors

RCF bound large data sample: evaluating the second derivative with the measured data and the ML estimates usual method for estimating the covariance matrix when the likelihood function is maximized numerically Ex: MINUIT (Cern Library) • finite differences • invert the matrix to get Vij

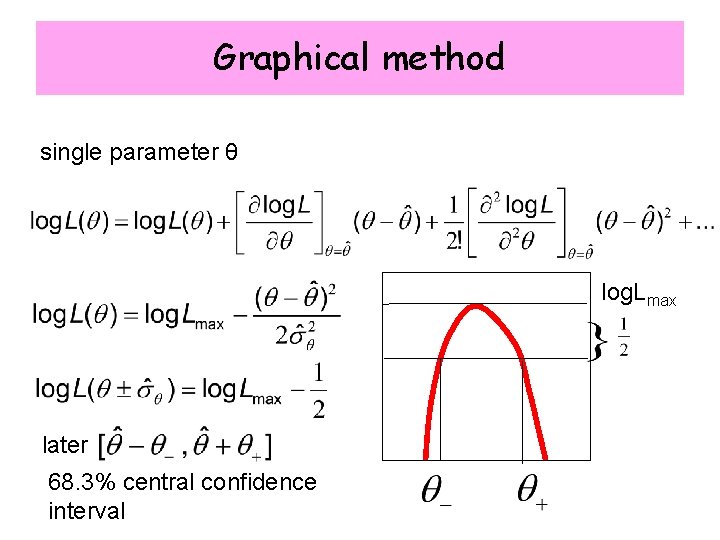
Graphical method single parameter θ log. Lmax later 68. 3% central confidence interval

ML with two parameters angular distribution for the scattering angles θ (x=cosθ) in a particle reaction. normalized -1≤ x ≤+1 realistic measurements only in xmin ≤ xmax

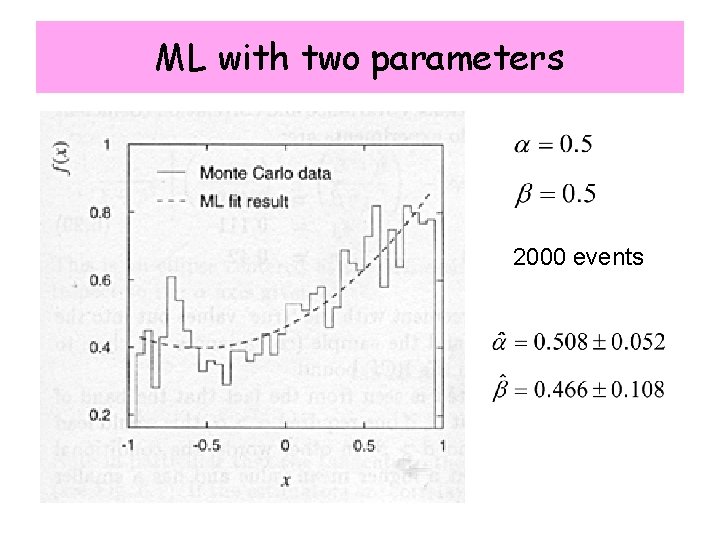
ML with two parameters 2000 events

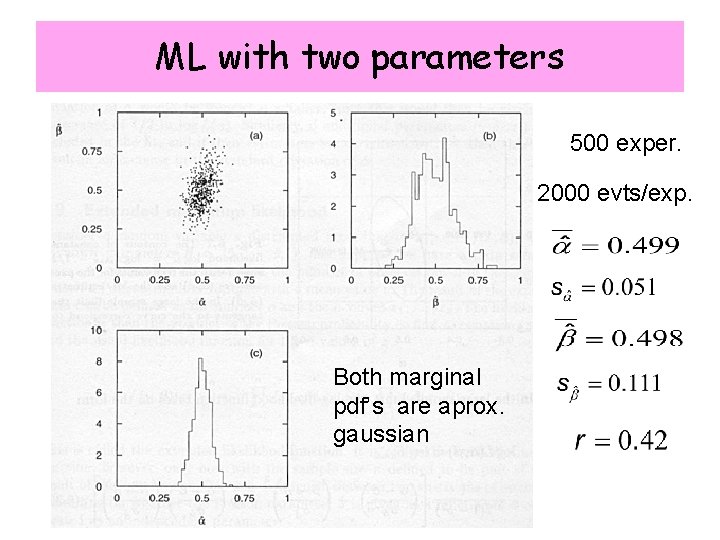
ML with two parameters 500 exper. 2000 evts/exp. Both marginal pdf’s are aprox. gaussian

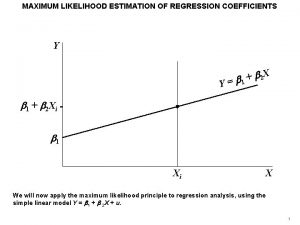
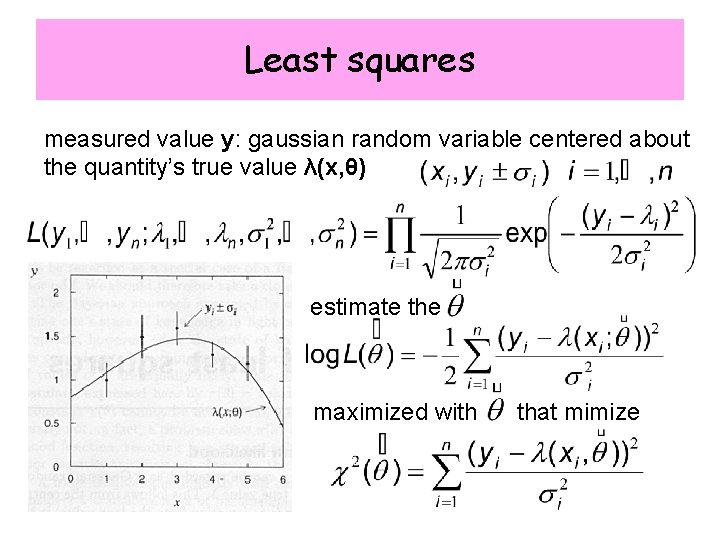
Least squares measured value y: gaussian random variable centered about the quantity’s true value λ(x, θ) estimate the maximized with that mimize

Least squares used to define the procedure even if yi are not gaussian measurements not independent, described by a n-dim Gaussian p. d. f. with nown cov. matrix but unknown mean values: LS estimators

Least squares linearly independent • estimators and their variances can be found analytically • estimators: zero bias and minimum variance minimum

Least squares covariance matrix for the estimators coincides with the RCF bound for the inverse covariance matrix if yi are gaussian distributed

Least squares linear in to interpret this, one single θ , quadratic in

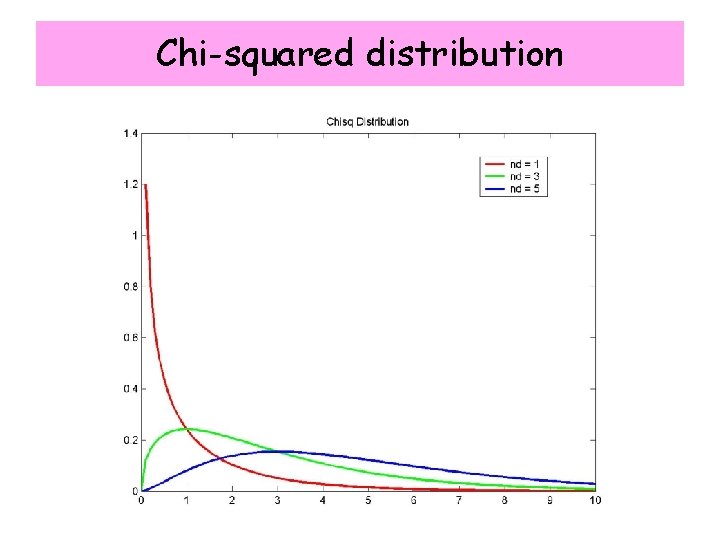
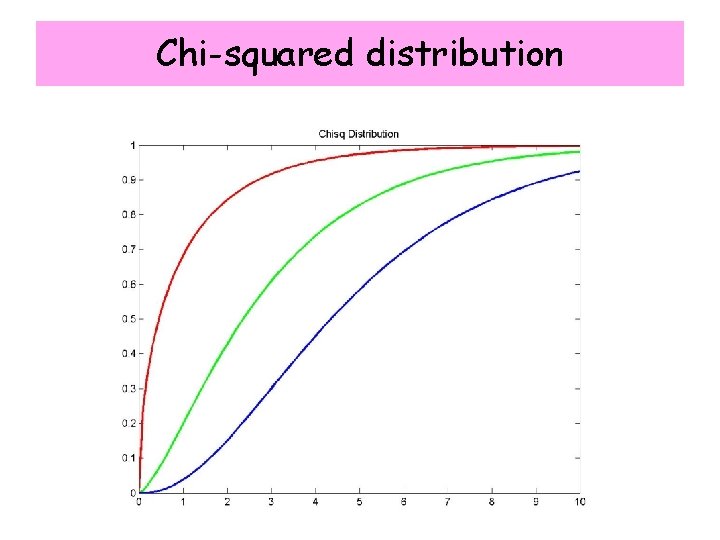
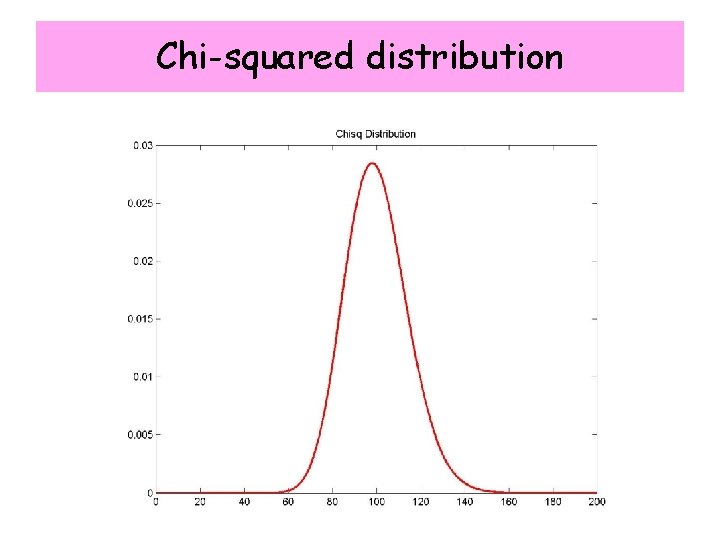
Chi-squared distribution n=1, 2, … 0 ≤ z ≤ ∞ (degrees of freedom) n independent gaussian random variables xi with known is distributed as a for n dof

Chi-squared distribution

Chi-squared distribution

Chi-squared distribution