CSCE 555 Bioinformatics Lecture 13 Phylogenetics II HAPPY

CSCE 555 Bioinformatics Lecture 13 Phylogenetics II HAPPY CHINESE NEW YEAR Meeting: MW 4: 00 PM-5: 15 PM SWGN 2 A 21 Instructor: Dr. Jianjun Hu Course page: http: //www. scigen. org/csce 555 University of South Carolina Department of Computer Science and Engineering 2008 www. cse. sc. edu.

Outline Review For Exams Data for Phylogenetic Tree inference Classification of Tree inference approaches Neighbor-joining algorithm Parsimony-based tree reconstruction Least Square Best-fit reconstruction 9/29/2020 2

Midterm, Midterm How to review: read slides and textbooks, especially CG book. Format of problems: examples ◦ Brief questions: what is the difference between global alignment and local alignment? ◦ calculation: build a HMM model for a multiple seq alignment ◦ Definition: blasting, Motif, ORF

Covered Topics Understand: ◦ ◦ ◦ ◦ ◦ concepts, algorithm ideas, tools Sequencing/blasting Gene finding Alignment algorithms and applications DNA motif search HMM profiles Gene prediction algorithms Promoter predictions Comparative genomics ……

Phylogenetic Reconstruction There are essentially two types of data for phylogenetic tree estimation: ◦ Distance data, usually stored in a distance matrix, e. g. DNA×DNA hybridisation data, morphometric differences, immunological data, pairwise genetic distances ◦ Character data, usually stored in a character array; e. g. multiple sequence alignment of DNA sequences, morphological characters. Characters Distances Taxa A B C D E 1 1234567890 Taxa A B C D E 1 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 0

Phylogenetic Reconstruction Given the huge number of possible trees even for small data sets, we have two options: ◦ Build one according to some clustering algorithm ◦ Assign a “goodness of fit” criterion (an objective function) and find the tree(s) which optimise(s) this criterion

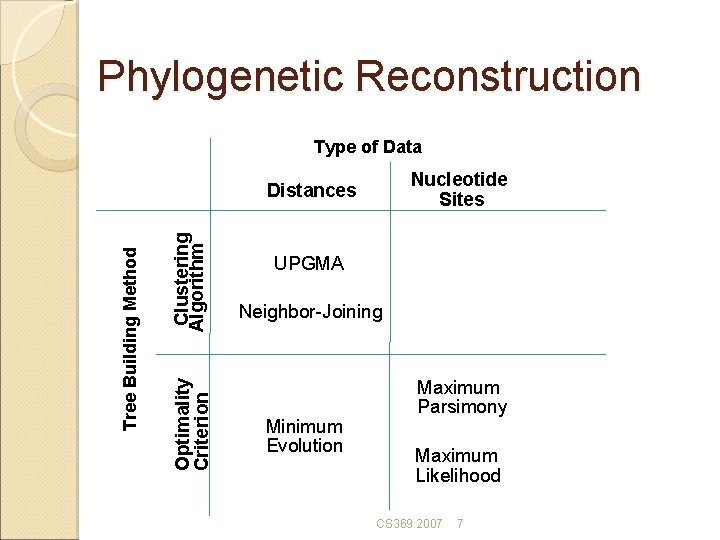
Phylogenetic Reconstruction Type of Data Nucleotide Sites Clustering Algorithm Optimality Criterion Tree Building Method Distances UPGMA Neighbor-Joining Minimum Evolution Maximum Parsimony Maximum Likelihood CS 369 2007 7

Phylogenetic Methods Many different procedures exist. Three of the most popular: Neighbor-joining • Minimizes distance between nearest neighbors Maximum parsimony • Minimizes total evolutionary change Maximum likelihood • Maximizes likelihood of observed data

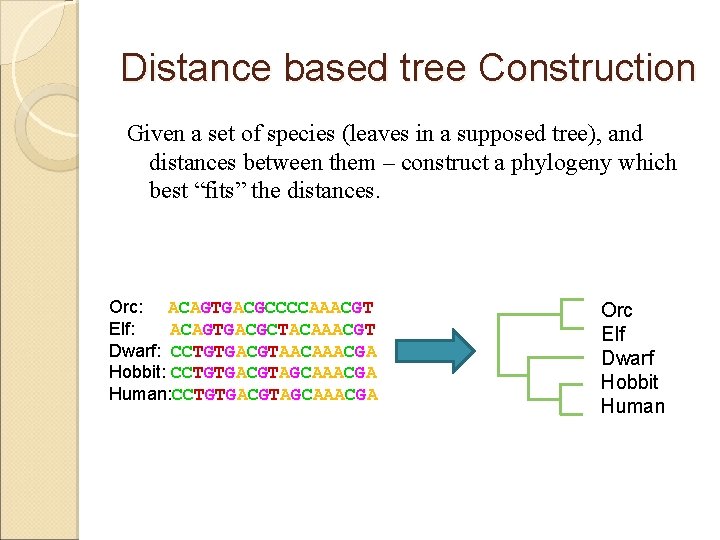
Distance based tree Construction Given a set of species (leaves in a supposed tree), and distances between them – construct a phylogeny which best “fits” the distances. Orc: ACAGTGACGCCCCAAACGT Elf: ACAGTGACGCTACAAACGT Dwarf: CCTGTGACGTAACAAACGA Hobbit: CCTGTGACGTAGCAAACGA Human: CCTGTGACGTAGCAAACGA Orc Elf Dwarf Hobbit Human

Distance Matrix Given n species, we can compute the n x n distance matrix Dij may be defined as the edit distance between a gene in species i and species j, where the gene of interest is sequenced for all n species. Dij can also be any other feature-based distances

Distances in Trees Edges may have weights reflecting: ◦ Number of mutations on evolutionary path from one species to another ◦ Time estimate for evolution of one species into another In a tree T, we often compute dij(T) - the length of a path between leaves i and j

Distances in Trees Edges may have weights reflecting: ◦ Number of mutations on evolutionary path from one species to another ◦ Time estimate for evolution of one species into another In a tree T, we often compute dij(T) - the length of a path between leaves i and j

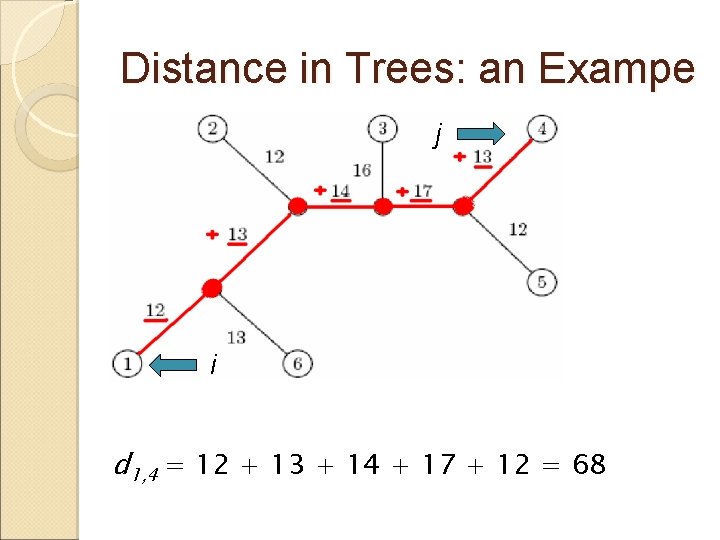
Distance in Trees: an Exampe j i d 1, 4 = 12 + 13 + 14 + 17 + 12 = 68

Fitting Distance Matrix Given n species, we can compute the n x n distance matrix Dij Evolution of these genes is described by a tree that we don’t know. We need an algorithm to construct a tree that best fits the distance matrix Dij

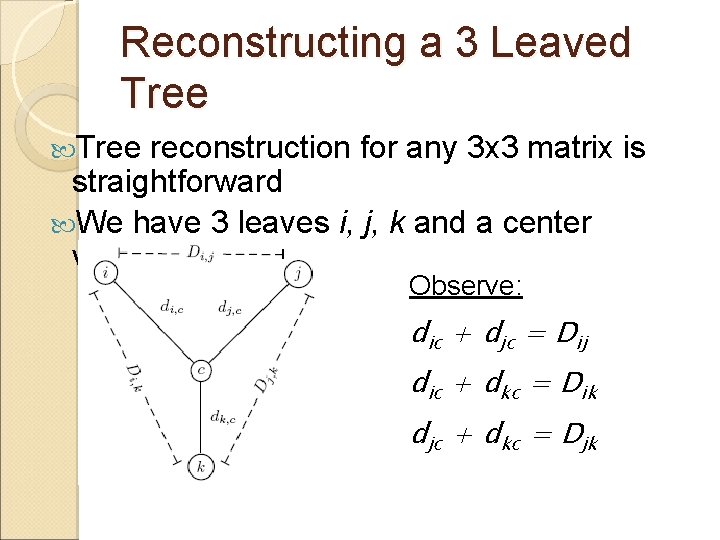
Reconstructing a 3 Leaved Tree reconstruction for any 3 x 3 matrix is straightforward We have 3 leaves i, j, k and a center vertex c Observe: dic + djc = Dij dic + dkc = Dik djc + dkc = Djk

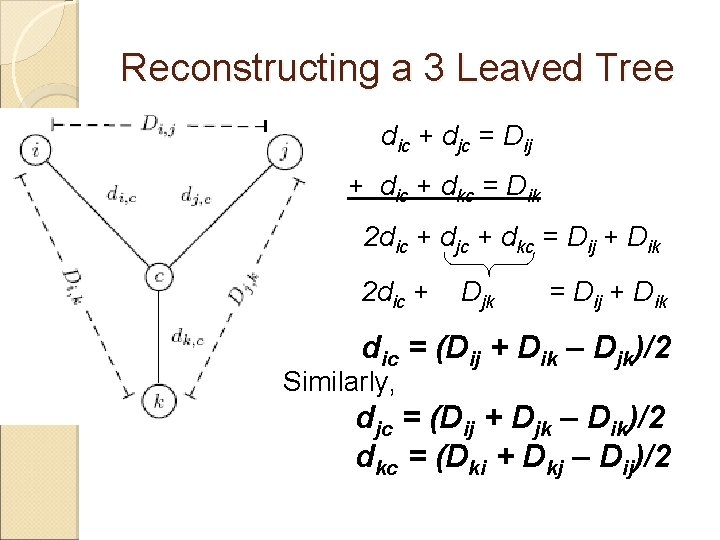
Reconstructing a 3 Leaved Tree dic + djc = Dij + dic + dkc = Dik 2 dic + djc + dkc = Dij + Dik 2 dic + Djk = Dij + Dik dic = (Dij + Dik – Djk)/2 Similarly, djc = (Dij + Djk – Dik)/2 dkc = (Dki + Dkj – Dij)/2

Trees with > 3 Leaves An tree with n leaves has 2 n-3 edges This means fitting a given tree to a distance matrix D requires solving a system of “n choose 2” equations with 2 n-3 variables This is not always possible to solve for n > 3

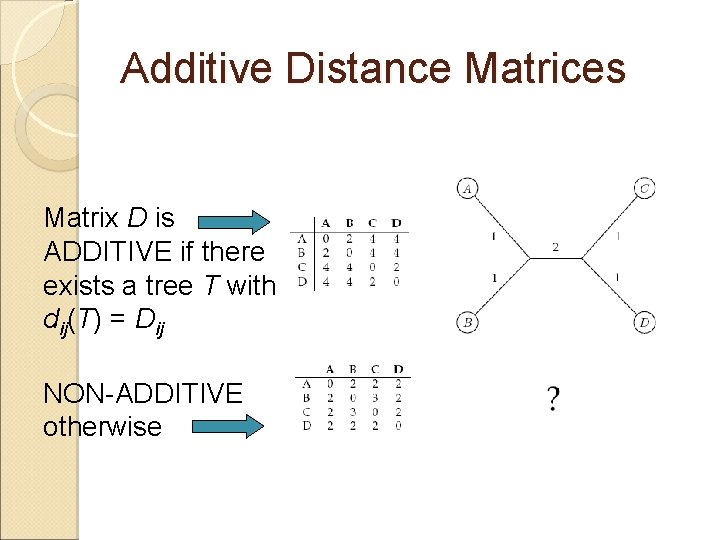
Additive Distance Matrices Matrix D is ADDITIVE if there exists a tree T with dij(T) = Dij NON-ADDITIVE otherwise

Distance Based Phylogeny Problem Goal: Reconstruct an evolutionary tree from a distance matrix Input: n x n distance matrix Dij Output: weighted tree T with n leaves fitting D If D is additive, this problem has a solution and there is a simple algorithm to solve it

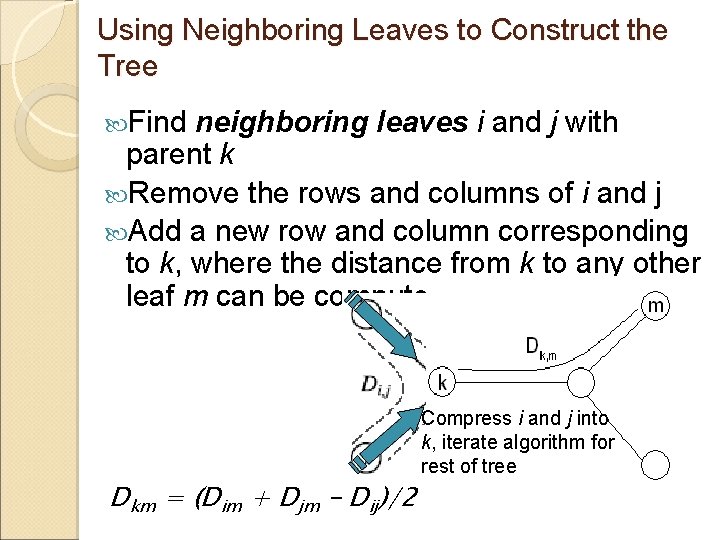
Using Neighboring Leaves to Construct the Tree Find neighboring leaves i and j with parent k Remove the rows and columns of i and j Add a new row and column corresponding to k, where the distance from k to any other leaf m can be computed as: Dkm = (Dim + Djm – Dij)/2 Compress i and j into k, iterate algorithm for rest of tree

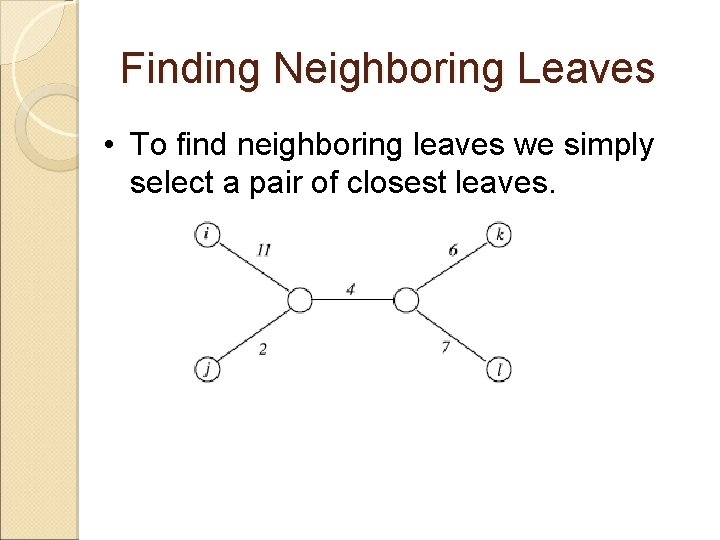
Finding Neighboring Leaves • To find neighboring leaves we simply select a pair of closest leaves.

Finding Neighboring Leaves • To find neighboring leaves we simply select a pair of closest leaves. WRONG

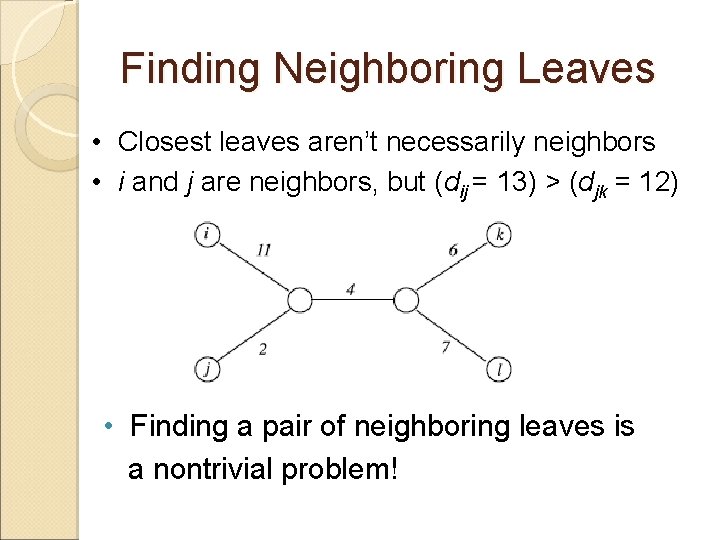
Finding Neighboring Leaves • Closest leaves aren’t necessarily neighbors • i and j are neighbors, but (dij = 13) > (djk = 12) • Finding a pair of neighboring leaves is a nontrivial problem!

Neighbor Finding: Seitou & Nei algorithm (1987) Definitions Theorem (Saitou & Nei) Assume all edge weights are positive. If D(i, j) is minimal (among all pairs of leaves), then i and j are neighboring leaves in the tree.

Neighbor Joining Algorithm In 1987 Naruya Saitou and Masatoshi Nei developed a neighbor joining algorithm for phylogenetic tree reconstruction Finds a pair of leaves that are close to each other but far from other leaves: implicitly finds a pair of neighboring leaves Advantages: works well for additive and other non-additive matrices, it does not have the flawed molecular clock assumption

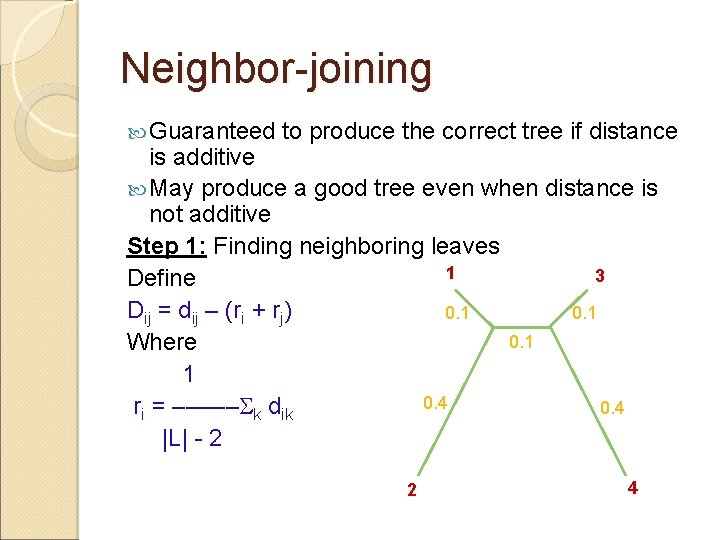
Neighbor-joining Guaranteed to produce the correct tree if distance is additive May produce a good tree even when distance is not additive Step 1: Finding neighboring leaves 1 3 Define Dij = dij – (ri + rj) 0. 1 Where 1 0. 4 ri = ––––– k dik 0. 4 |L| - 2 2 4

Algorithm: Neighbor-joining Initialization: Define T to be the set of leaf nodes, one per sequence Let L = T Iteration: Pick i, j s. t. Dij is minimal Define a new node k, and set dkm = ½ (dim + djm – dij) for all m L Add k to T, with edges of lengths dik = ½ (dij + ri – rj) Remove i, j from L; Add k to L Termination: When L consists of two nodes, i, j, and the edge between them of length d

Rooting a tree, and definition of outgroup Neighbor-joining produces an unrooted tree How do we root a tree between N species using n-j? An outgroup is a species that we know to be more distantly related to all remaining species, than they are to one another Example: Human, mouse, rat, pig, dog, chicken, 1 whale 4 Which one is an outgroup? Outgroup can act as a root 2 3

Neighbor Joining Algorithm-Widely Used Applicable Known The to matrices which are not additive to work good in practice algorithm and its variants are the most widely used distance-based algorithms today.

Maximum Parsimony Method for Tree Inference A Character-based method Input: h sequences (one per species), all of length k. Goal: Find a tree with the input sequences at its leaves, and an assignment of sequences to internal nodes, such that the total number of substitutions is minimized. Two sub-problems: 1. Find the parsimony cost of a given tree (easy) 2. Search through all tree topologies (hard)

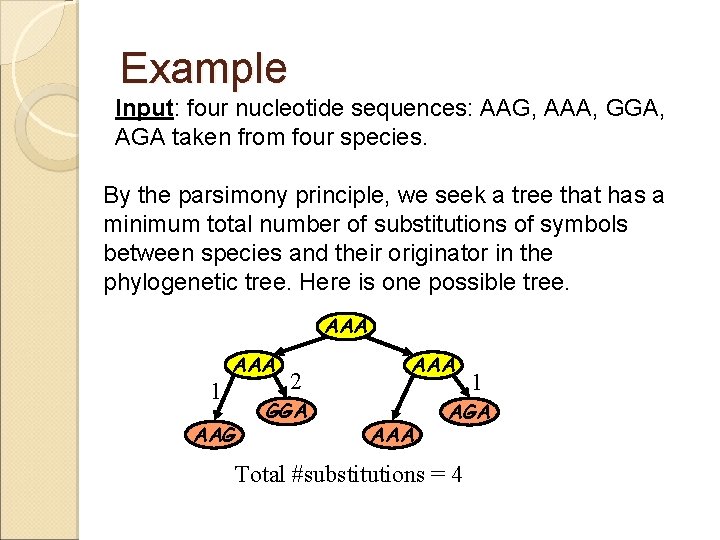
Example Input: four nucleotide sequences: AAG, AAA, GGA, AGA taken from four species. By the parsimony principle, we seek a tree that has a minimum total number of substitutions of symbols between species and their originator in the phylogenetic tree. Here is one possible tree. AAA 1 AAA AAG 2 GGA AAA 1 AGA Total #substitutions = 4

Least Squares Distance Phylogeny Problem If the distance matrix D is NOT additive, then we look for a tree T that approximates D the best: Squared Error : ∑i, j (dij(T) – Dij)2 Squared Error is a measure of the quality of the fit between distance matrix and the tree: we want to minimize it. Least Squares Distance Phylogeny Problem: finding the best approximation tree T for a nonadditive matrix D (NP-hard).

Search through tree topologies: Branch and Bound Observation: adding an edge to an existing tree can only increase the parsimony cost Enumerate all unrooted trees with at most n leaves: [i 3][i 5][i 7]……[i 2 N– 5]] where each ik can take values from 0 (no edge) to k At each point keep C = smallest cost so far for a complete tree Start B&B with tree [1][0][0]……[0] Whenever cost of current tree T is > C, then: ◦ T is not optimal ◦ Any tree with more edges containing T, is not optimal: Increment by 1 the rightmost nonzero counter

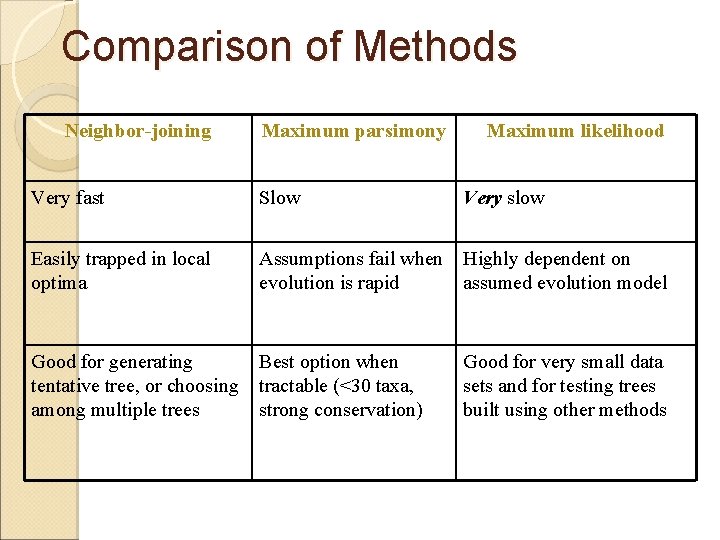
Comparison of Methods Neighbor-joining Maximum parsimony Maximum likelihood Very fast Slow Very slow Easily trapped in local optima Assumptions fail when Highly dependent on evolution is rapid assumed evolution model Good for generating tentative tree, or choosing among multiple trees Best option when tractable (<30 taxa, strong conservation) Good for very small data sets and for testing trees built using other methods

Summary Category of phylogenetic inference algorithms Neighbor-joining algorithm

Acknowledgement Anonymous authors