The principle of inclusion and exclusion inversion formulae

The principle of inclusion and exclusion; inversion formulae Speaker: 藍國元 Date: 2005. 11. 28

Outline • • • An overview of principle of inclusion-exclusion Principle of inclusion-exclusion Applications of PIE Möbius Inversion formula Applications of MIF

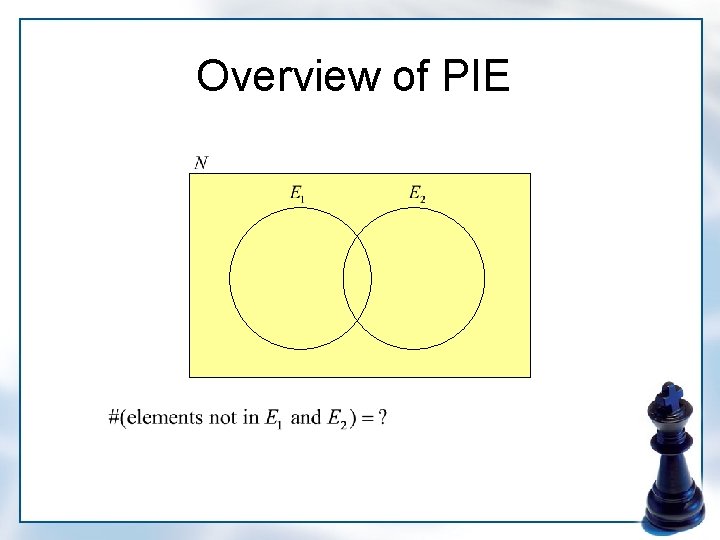
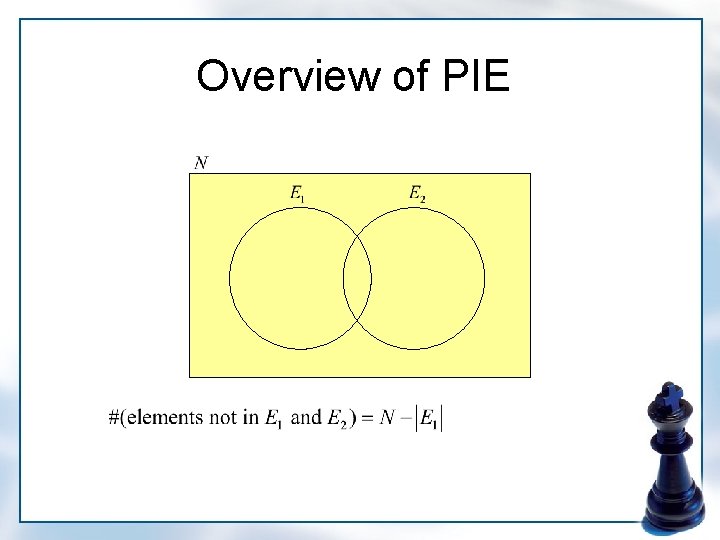
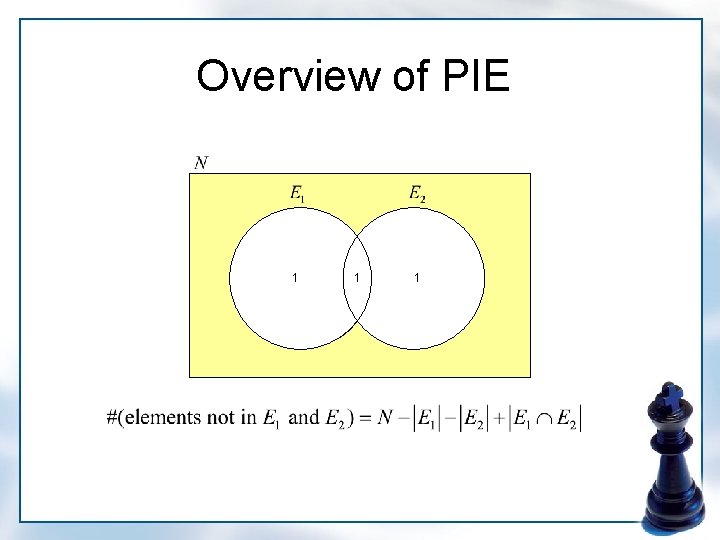
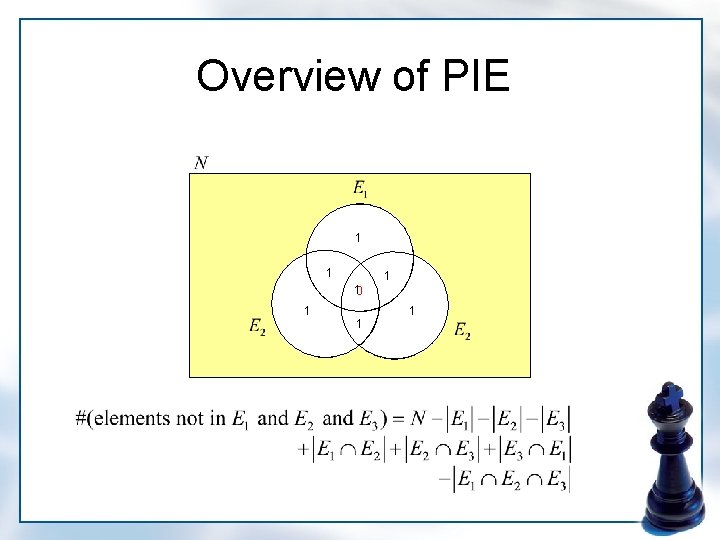
Overview of PIE

Overview of PIE 1 1

Overview of PIE 1 2 1 1

Overview of PIE 1 1 1

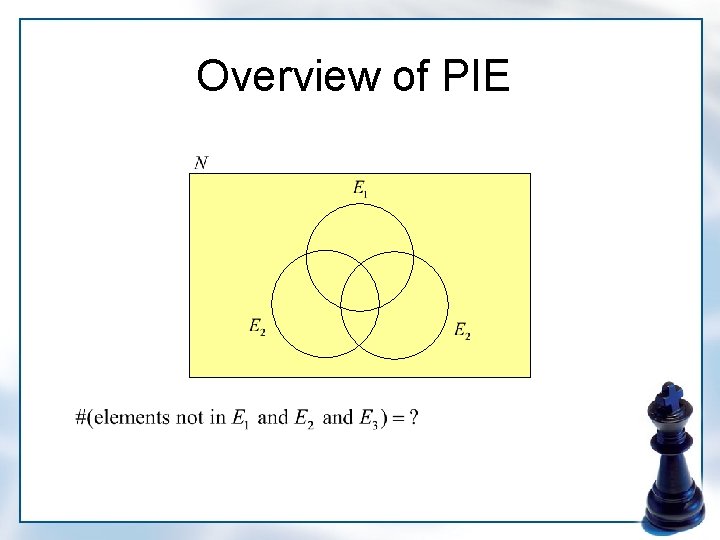
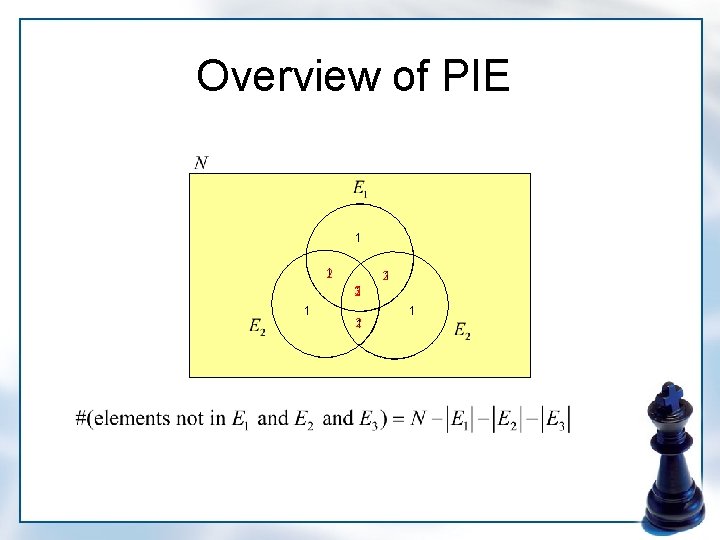
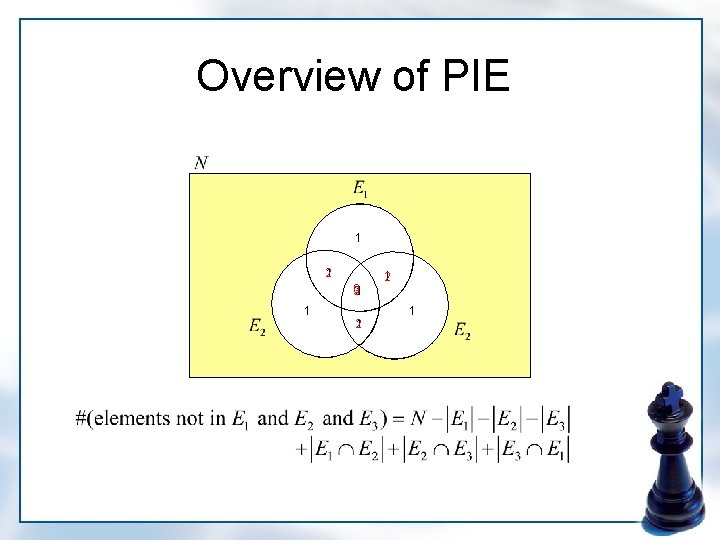
Overview of PIE

Overview of PIE 1 1 2 21 31 2 1 21 1

Overview of PIE 1 2 1 0 21 3 1 1 21

Overview of PIE 1 10 1 1 1

Principle of Inclusion-Exclusion • Notations: – – S: a set of N-elements E 1, E 2, …, Er: not necessarily distinct subsets of S N(M): # of elements of S in for Nj

Principle of Inclusion-Exclusion • Theorem 1 (PIE) Proof: Case 1. and is in none of contributes 1 to left-hand side and right-hand side. Case 2. and is in exactly k of the sets contributes 0 to left-hand. The contribution of to right-hand side equals

Principle of Inclusion-Exclusion • Theorem (Purest form of PIE) Let be an n-set. Let be the 2 n-dimensional vector space (over some field K) of all functions. Let be the linear transformation defined by Then exists and is given by

Principle of Inclusion-Exclusion • Combinatorial situation involving previous Theorem : given set : properties set : subset of : # of objects in that have exactly the properties in : # of objects in that have at least the properties in

Principle of Inclusion-Exclusion • Combinatorial situation involving previous Theorem Then we have By previous Theorem In particular,

Principle of Inclusion-Exclusion • Dual form We can reformulate the PIE by interchanging with , and so on. : # of objects in Then we have , that have at most the properties in

Applications of PIE • Application 1: Derangements How many permutations have no fixed points? i. e. Sol: Let We have By PIE,

Applications of PIE • Application 1: Derangements Since , is a good approximation of From it is not difficult to derive

Applications of PIE • Application 2: Surjections Give X be an n-set and Y surjection of X to Y? Sol: Let We have By PIE, be a k-set. How many

Applications of PIE • Application 2: Surjections Note that if k > n then if k = n then Note that where S(n, k) is the Stirling number of second kind.

Applications of PIE • Application 3: Show that Combinatorial proof: Let be an n-set of blue balls be an m-set of red balls. How many k-subsets consist of red balls only? The answer is trivially the right-hand side. The left-hand side is letting S be all the k-subset of X∪Y and Ei those k-subset that contain bi and then PIE gives the left-hand side.

Applications of PIE • Application 3: Show that Algebra proof: We use the expansion: The coefficient of in is

Applications of PIE • Application 4: Euler function Let be a positive integer and number of integers k with such that Show that Proof: Let We have By PIE, be the

• Theorem 2 [Gauss] Let with. Then Proof: Let Since every integer from 1 to n belongs only one , we have Since d runs all positive divisor of n, we have

• Example We show that We have

Möbius Inversion formula • Definition Let with . The Möbius function, denoted by 1, 0, , Note that satisfies is if n =1 if if is called squarefree.

Möbius Inversion formula • Theorem 3 Let with . 1, if n =1 0, otherwise Proof: There is nothing to show when n=1. If , then

Möbius Inversion formula • Remarks Using the Möbius function, we can reformulate as

Möbius Inversion formula • Definition An arithmetic function is a function whose domain is the set of positive integers. • Example – – –

Möbius Inversion formula • Theorem 4 (Möbius Inversion Formula) Let be arithmetic functions. Then if and only if

Möbius Inversion formula • Theorem 4 (Möbius Inversion Formula) Proof: the inner sum is 0 unless

Möbius Inversion formula • Theorem 4 (Möbius Inversion Formula) Proof: the inner sum is 0 unless

Applications of MIF • The Möbius Inversion Formula can be used to obtain nontrivial identities among arithmetic functions from trivial identities among arithmetic functions.

Applications of MIF • Example 1 Let with and let for all such n. We have By MIF, we obtain the nontrivial identity or , equivalently

Applications of MIF • Example 2 Let with and let . We have By MIF, we obtain the nontrivial identity

Applications of MIF • Example 3 Let with and let . We have By MIF, we obtain the nontrivial identity

-END-