TESTES DE HIPTESES Testes de Hipteses Um dos

TESTES DE HIPÓTESES

Testes de Hipóteses Um dos problemas a serem resolvidos pela inferência estatística é o de testar uma hipótese. Isto é, feita determinada afirmação sobre uma população, desejamos saber se os resultados experimentais provenientes de uma amostra contrariam ou não tal afirmação. O objetivo do teste estatístico de hipóteses é, então, fornecer uma metodologia que nos permita verificar se os dados amostrais trazem evidências que apóiam ou não a hipótese (estatística) formulada.

Hipóteses De uma maneira geral, uma hipótese estatística é uma afirmação sobre um parâmetro ou a forma da distribuição de uma variável aleatória (característica de interesse da população). Hipótese nula (H) versus Hipótese alternativa (A)

Testar uma hipótese estatística é estabelecer uma regra que nos permita, com base na informação de uma amostra, decidir pela rejeição ou não de H. Usando a teoria estatística e as informações disponíveis, elegemos uma estatística a ser usada para testar H.

Erros Erro tipo I: Rejeitar H quando H é verdadeira Erro tipo II: Não rejeitar H quando H é falsa Probabilidades de erros P(erro I) = P(rejeitar H | H é verdadeira) = : nível de significância do teste P(erro II) = P(não rejeitar H | H é falsa) =

Passos para a construção de um teste de hipóteses Passo 1. Fixe as hipóteses H e A. Passo 2. Decida qual será a estatística de teste a ser usada para testar H. Passo 3. Fixe a probabilidade α de cometer o erro de tipo I. Passo 4. Use as observações da amostra para calcular o valor da estatística de teste. Passo 5. Calcule o nível descritivo P associado ao valor observado da estatística de teste. P é a probabilidade de rejeitar H quando H é verdadeira tomando como base o valor observado da estatística de teste.

Testes de Aderência

1. Teste Qui-quadrado Temos uma amostra X 1, X 2, …, Xn de uma característica de interesse X associada à uma população. Queremos testar a hipótese H: A distribuição de X é P 0, onde P 0 é uma distribuição especificada. A hipótese H é equivalente à H: p 1=p 10, p 2=p 20, …, ps=ps 0, onde pi 0 são probabilidades conhecidas que especificam P 0. Vamos construir uma tabela da seguinte forma: Categoria A 1 Freq. Observada O 1 Freq. Esperada E 1 A 2. . . O 2. . . E 2. . . As Os Es Total n n

A estatística de teste é dada por onde Oi representa o valor observado para a categoria Ai e Ei representa o valor esperado, sob H, para a categoria Ai. Temos Ei = npi 0, i=1, …, s. Se H for verdadeira, a estatística de teste tem distribuição qui-quadrado com (s-m-1) graus de liberdade, sendo m o número de parâmetros que estimamos a partir da amostra.

Exemplo 1. Consideremos os dados abaixo, que supostamente são uma amostra de tamanho n = 30 de uma distribuição normal. Os dados já estão ordenados. 1, 04 1, 73 3, 93 4, 44 6, 37 6, 51 7, 64 8, 18 8, 48 8, 57 8, 65 9, 71 9, 87 9, 95 10, 01 10, 52 10, 69 11, 72 12, 17 12, 61 12, 98 13, 03 13, 16 14, 11 14, 60 14, 64 14, 75 16, 68 22, 14 Vamos construir as seguintes categorias: A 1: até Q 1 A 2: de Q 1 até Q 2 A 3: de Q 2 até Q 3 A 4: maior ou igual a Q 3, onde Q 1, Q 2 e Q 3 são os quartis (teóricos) da normal.

Encontramos Q 3 = 13, 26. , s = 4, 5, Q 1 = 7, 14, Q 2 = 10, 2 e Categoria (≤ 7, 14) (7, 14; 10, 2) (10, 2; 13, 26) (≥ 13, 26) n Oi 6 10 8 6 30 Ei 7, 5 30 Lembre que pi 0 = 0, 25 para todo i. Temos . Fixado α = 0, 05, temos Como 1, 47 não pertence à Rc, não rejeitamos a hipótese de que os dados seguem uma distribuição normal. .

O nível descritivo P do teste é dado por (calculado com o auxílio do Minitab). Como P > 0, 05, não rejeitamos a hipótese de que os dados seguem uma distribuição normal.

Exercício. Teste, para o nível α = 0, 01, se os dados abaixo provêm de uma distribuição exponencial. 0, 378 1, 007 0, 228 0, 123 0, 391 0, 470 0, 389 0, 089 0, 458 0, 368 0, 627 0, 646 0, 063 0, 831 0, 480 0, 093 0, 009 0, 387 0, 093 0, 400

Teste de Kolmogorov-Smirnov Temos uma amostra X 1, X 2, …, Xn de uma característica de interesse X associada à uma população. Queremos testar a hipótese H: X tem uma determinada distribuição contínua versus A: X não tem essa distribuição contínua.

O teste de Kolmogorov-Smirnov é realizado da seguinte forma: • Ordenamos os n valores xi observados do conjunto de dados. • Para cada valor observado xi da característica X calculamos F(xi)=P(X<xi) usando como distribuição de X aquela especificada em H. • Em seguida, calculamos a função acumulada empírica Fe(xi) =i/n. • A estatística de Kolmogorov – Smirnov é dada pelo máximo dos valores absolutos das diferenças D =|F(xi)- Fe(xi)|.

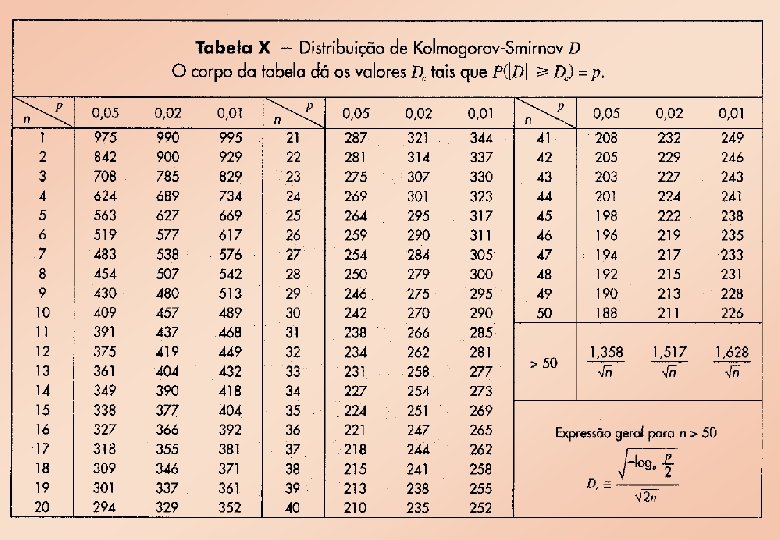
• Fixado um nível de significância α, definimos uma região crítica Rc para o teste, ou seja, Rc={D>Dc}, onde Dc vem da Tabela X. Se Dobs pertencer à Rc, rejeitamos a hipótese H.

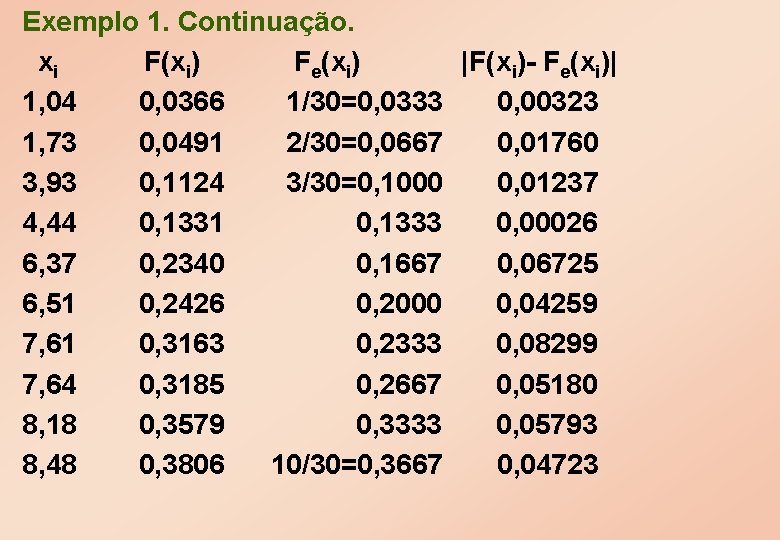
Exemplo 1. Consideremos os dados abaixo que supostamente são uma amostra de tamanho n = 30 de uma distribuição normal com média igual a 10 e desvio padrão igual a 5. Os dados já estão ordenados. 1, 04 1, 73 3, 93 4, 44 6, 37 6, 51 7, 64 8, 18 8, 48 8, 57 8, 65 9, 71 9, 87 9, 95 10, 01 10, 52 10, 69 11, 72 12, 17 12, 61 12, 98 13, 03 13, 16 14, 11 14, 60 14, 64 14, 75 16, 68 22, 14

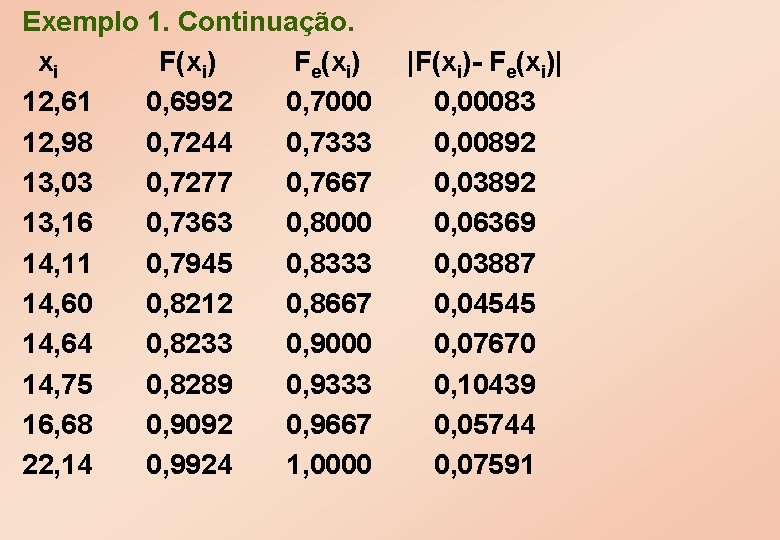
Exemplo 1. Continuação. xi F(xi) Fe(xi) |F(xi)- Fe(xi)| 1, 04 0, 0366 1/30=0, 0333 0, 00323 1, 73 0, 0491 2/30=0, 0667 0, 01760 3, 93 0, 1124 3/30=0, 1000 0, 01237 4, 44 0, 1331 0, 1333 0, 00026 6, 37 0, 2340 0, 1667 0, 06725 6, 51 0, 2426 0, 2000 0, 04259 7, 61 0, 3163 0, 2333 0, 08299 7, 64 0, 3185 0, 2667 0, 05180 8, 18 0, 3579 0, 3333 0, 05793 8, 48 0, 3806 10/30=0, 3667 0, 04723

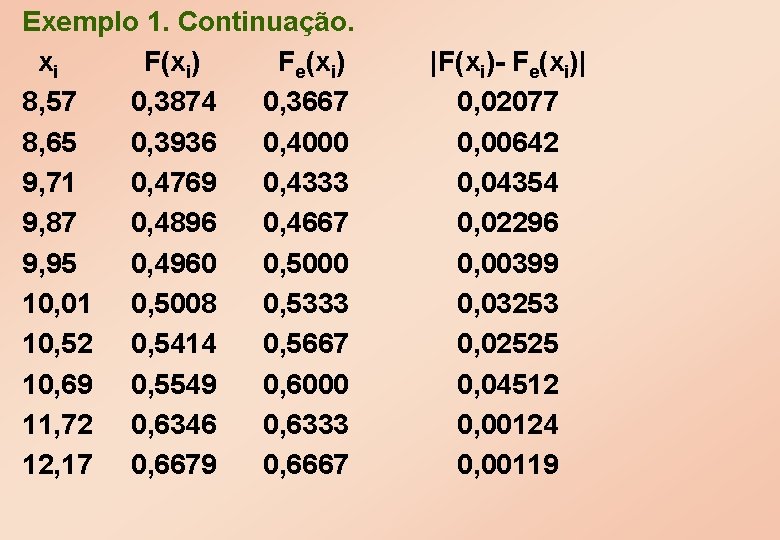
Exemplo 1. Continuação. xi F(xi) Fe(xi) 8, 57 0, 3874 0, 3667 8, 65 0, 3936 0, 4000 9, 71 0, 4769 0, 4333 9, 87 0, 4896 0, 4667 9, 95 0, 4960 0, 5000 10, 01 0, 5008 0, 5333 10, 52 0, 5414 0, 5667 10, 69 0, 5549 0, 6000 11, 72 0, 6346 0, 6333 12, 17 0, 6679 0, 6667 |F(xi)- Fe(xi)| 0, 02077 0, 00642 0, 04354 0, 02296 0, 00399 0, 03253 0, 02525 0, 04512 0, 00124 0, 00119

Exemplo 1. Continuação. xi F(xi) Fe(xi) 12, 61 0, 6992 0, 7000 12, 98 0, 7244 0, 7333 13, 03 0, 7277 0, 7667 13, 16 0, 7363 0, 8000 14, 11 0, 7945 0, 8333 14, 60 0, 8212 0, 8667 14, 64 0, 8233 0, 9000 14, 75 0, 8289 0, 9333 16, 68 0, 9092 0, 9667 22, 14 0, 9924 1, 0000 |F(xi)- Fe(xi)| 0, 00083 0, 00892 0, 03892 0, 06369 0, 03887 0, 04545 0, 07670 0, 10439 0, 05744 0, 07591

O valor máximo dos valores absolutos das diferenças é Dobs = 0, 1044. Da tabela X, temos, para α = 0, 05, o valor crítico Dc= 0, 242. Logo Rc = {D > 0, 242} e, como 0, 1044 não pertence à Rc, aceitamos H, ou seja, os dados seguem uma distribuição normal com média 10 e desvio padrão igual a 5.

Exercício. Teste, para o nível α = 0, 01, se os dados abaixo provêm de uma distribuição exponencial com média 0, 5. 0, 009 0, 123 0, 389 0, 480 0, 024 0, 228 0, 391 0, 627 0, 063 0, 368 0, 400 0, 646 0, 089 0, 378 0, 458 0, 831 0, 093 0, 387 0, 470 1, 007