Temperature and Heat Loss Thermal conductivity Thermal conductivity

Temperature and Heat Loss Thermal conductivity: Thermal conductivity or λ-value (also known as k -value) of a material is a measure of the rate at which heat is conducted through it under specified conditions. Flow of heat through a material is directly proportional to: θ 2 • surface area (A) • temperature difference between the opposite faces (θ 2 – θ 1) Heat • time for which heat flows (t) in, Q Flow of heat is indirectly proportional to the thickness of material (d) θ 1 Heat out A d Combining the above factors, the amount of heat flowing through a material, Q, is proportional to: (see next slide)

Temperature and Heat Loss Q = where λ (or k) is thermal conductivity of the material (continued)

Temperature and Heat Loss To work out the unit of thermal conductivity, the symbols in the equation are replaced with appropriate units: • Quantity of heat, Q: Joules (J) • Thickness of material, d: m • Time during which heat flows, t: seconds (s) • Surface area of the material, A: m 2 • Temperature difference, θ 2 – θ 1 = ºC or K

Temperature and Heat Loss Thermal conductivity (λ) is the rate at which heat is conducted through a material of unit measurements, to maintain the opposite faces of the materials at a temperature difference of 1 ºC. Thermal resistivity (r) is the reciprocal of thermal conductivity. Thermal resistance (R) takes into account the thickness of the material. where d is the thickness of the material in metres

Temperature and Heat Loss The Total Thermal Resistance of a material is a combination of material resistance and surface resistance Material resistance: All materials offer some resistance to the transmission of heat. Material resistance = d/λ Unit: m 2 K/W Surface resistance: The surfaces of all building materials have irregularities which trap air. Stationary layers of air are formed which resist the transmission of heat. Building material Outside surface (Rso) Inside surface (Rsi)

Temperature and Heat Loss Airspace resistance (Rairspace): If there is a cavity in a component, the airspace resistance needs to be considered as well, for example in a double glazed window, cavity wall etc. The airspace resistance depends on the width of the cavity. Glass Airspace Double-glazed window

Temperature and Heat Loss The total thermal resistance of a component is given by: Rtotal = Rsi + Rmaterials + Rairspace + Rso Where Rtotal is the total thermal resistance Rsi is thermal resistance of the inside surface Rmaterials is thermal resistance of the materials Rairspace is thermal resistance of the cavity Rso is thermal resistance of the outside surface

Temperature and Heat Loss Thermal transmittance or the U-value indicates the amount of heat energy that will flow per second through one square metre of a building element when the temperature difference between the inside and outside surfaces is one Kelvin (or 1 ºC). The U-value of an element/component can be determined from the following relationship: Unit: W/m 2 K

Temperature and Heat Loss The following topics are covered in this presentation: • Calculation of U-values • Heat loss from the building envelope • Use of U-values in heat loss calculations

Temperature and Heat Loss 1. Calculate the U-value of a) single-glazed window b) double-glazed window. Given: Thickness of glass = 4 mm Thermal conductivity of glass = 1. 02 W/m. K Thermal resistance of surfaces: 0. 12 (inside); 0. 06 (outside) Thermal resistance of 20 mm wide airspace = 0. 18 m 2 K/W Solution: The total thermal resistance of a component is given by: Rtotal = Rsi + Rmaterials + Rairspace + Rso where Rtotal is the total thermal resistance Rsi is thermal resistance of the inside surface Rmaterials is thermal resistance of the materials Rairspace is thermal resistance of the cavity Rso is thermal resistance of the outside surface

Temperature and Heat Loss a) Single-glazed window: Rtotal = Rsi + Rglass + Rso (no airspace in this case) = 0. 1839 m 2 K/W U-value = 1/R = 5. 44 W/m 2 K

Temperature and Heat Loss b) Double-glazed window: Rtotal = Rsi + Rglass + Rairspace + Rglass + Rso = 0. 12 + 0. 0039 + 0. 18 + 0. 0039 + 0. 06 = 0. 3678 U-value = 1/Rtotal = 2. 72 W/m 2 K

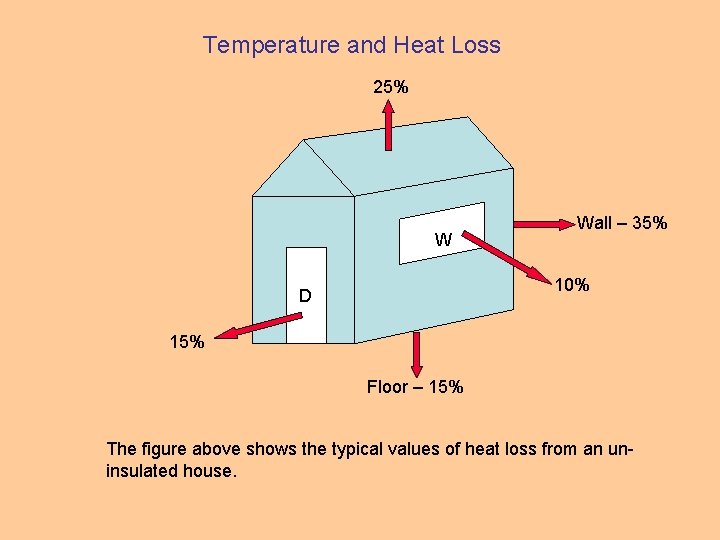
Temperature and Heat Loss 25% W Wall – 35% 10% D 15% Floor – 15% The figure above shows the typical values of heat loss from an uninsulated house.

1. Temperature and Heat Loss HEAT LOSS FROM A BUILDING: Heat loss from a building is determined in two parts; the first part is the FABRIC HEAT LOSS and the second is called HEAT LOSS BY VENTILATION. Fabric Heat Loss: The unit of U-value is: W/m 2 K This can be written as U = W/m 2 K After transposition, W = U × m 2 × K Replacing m 2 by A (area) and K by T (temperature difference): W=U×A×T where W is the heat loss in Watts. For determining the heat loss from an element/component we need to know its U-value, the surface area and the difference between the inside and outside temperatures.

2. Temperature and Heat Loss The heat loss due to ventilation occurs when the warm air of a room is replaced by cold, but fresh, air from outside. Rate of heat loss due to ventilation = where Cv is the volumetric specific heat capacity of air V is the volume of the room N is the number of air changes per hour T is the difference between inside and outside air temperatures Total rate of heat loss = Fabric heat loss + Ventilation heat loss

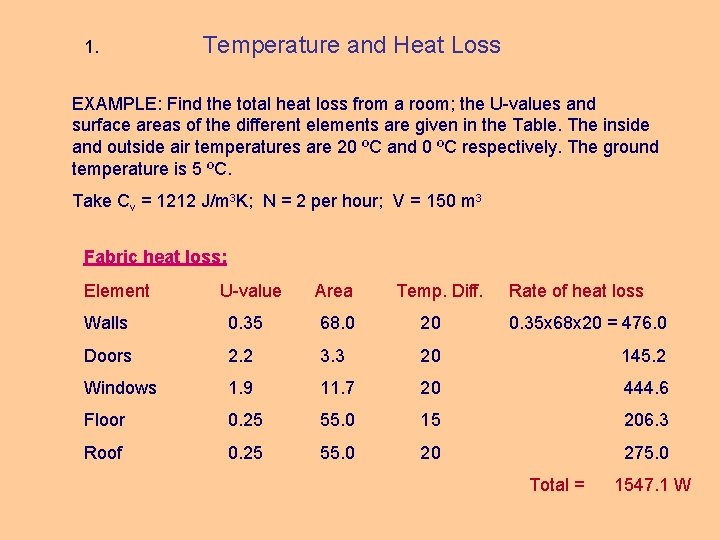
1. Temperature and Heat Loss EXAMPLE: Find the total heat loss from a room; the U-values and surface areas of the different elements are given in the Table. The inside and outside air temperatures are 20 ºC and 0 ºC respectively. The ground temperature is 5 ºC. Take Cv = 1212 J/m 3 K; N = 2 per hour; V = 150 m 3 Fabric heat loss: Element U-value Area Temp. Diff. Rate of heat loss Walls 0. 35 68. 0 20 0. 35 x 68 x 20 = 476. 0 Doors 2. 2 3. 3 20 145. 2 Windows 1. 9 11. 7 20 444. 6 Floor 0. 25 55. 0 15 206. 3 Roof 0. 25 55. 0 20 275. 0 Total = 1547. 1 W

Temperature and Heat Loss 2. Heat loss due to ventilation: Heat loss = = 2020. 0 W Total Heat Loss = 1547. 1 + 2020. 0 = 3567. 1 W or 3567. 1 J/s (1 W = 1 J/s)