Support Vector Machines Classification Algorithms and Applications Olvi

Support Vector Machines: Classification Algorithms and Applications Olvi L. Mangasarian Department of Mathematics -UCSD with G. M. Fung , Y. -J. Lee, J. W. Shavlik , W. H. Wolberg University of Wisconsin – Madison and Collaborators at Exon. Hit – Paris

What is a Support Vector Machine? v An optimally defined surface v Linear or nonlinear in the input space v Linear in a higher dimensional feature space v Implicitly defined by a kernel function v K(A, B) C

What are Support Vector Machines Used For? v Classification v Regression & Data Fitting v Supervised & Unsupervised Learning

Principal Topics v. Proximal support vector machine classification ØClassify by proximity to planes instead of halfspaces v. Massive incremental classification ØClassify by retiring old data & adding new data v. Knowledge-based classification ØIncorporate expert knowledge into a classifier v. Fast Newton method classifier ØFinitely terminating fast algorithm for classification v. RSVM: Reduced Support Vector Machines ØKernel size reduction (up to 99%) by random projection v. Breast cancer prognosis & chemotherapy ØClassify patients based on distinct survival curves Ø Isolate a class of patients that may benefit from

Principal Topics v. Proximal support vector machine classification

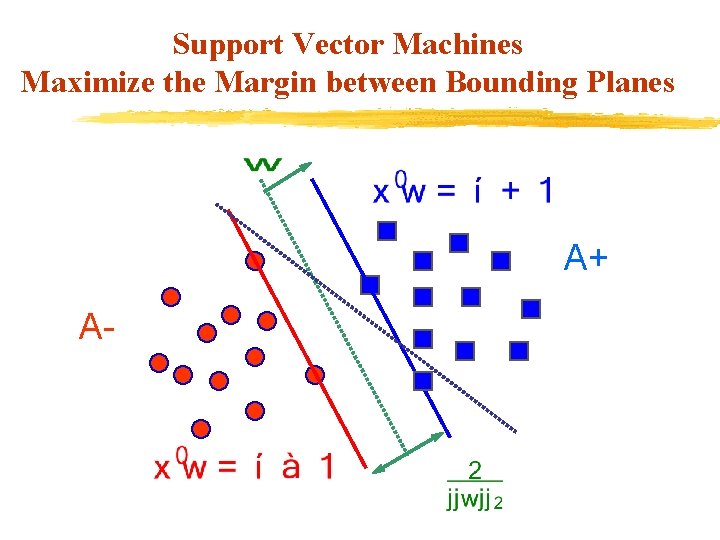
Support Vector Machines Maximize the Margin between Bounding Planes A+ A-

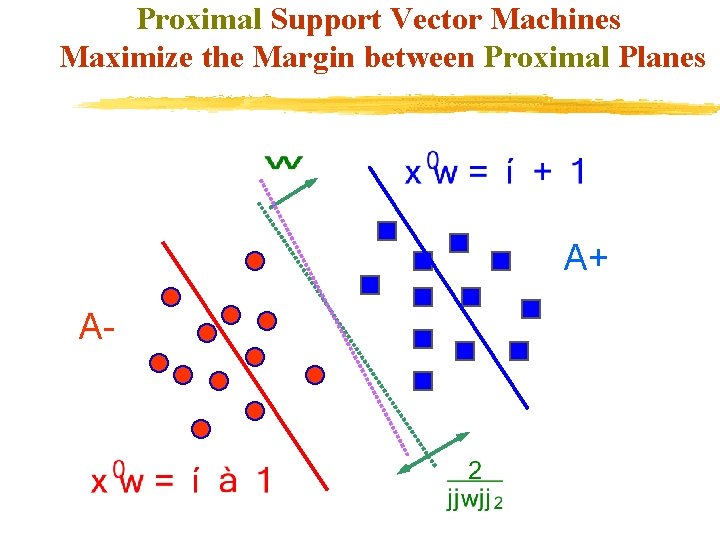
Proximal Support Vector Machines Maximize the Margin between Proximal Planes A+ A-

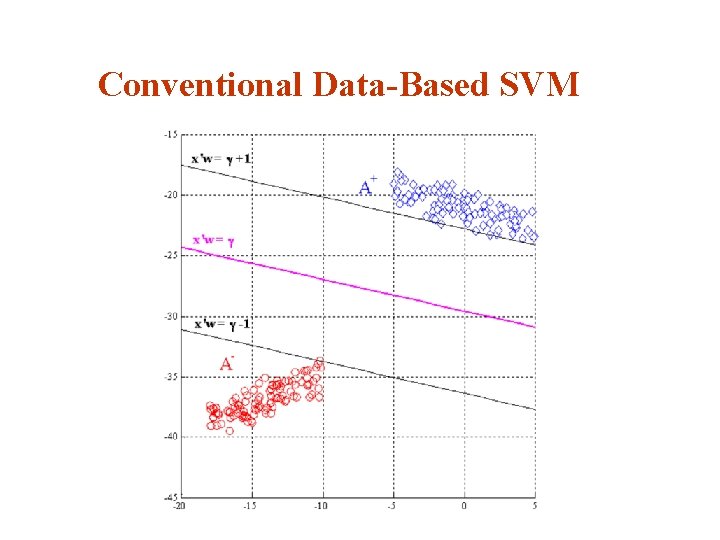
Standard Support Vector Machine Algebra of 2 -Category Linearly Separable Case v Given m points in n dimensional space v Represented by an m-by-n matrix A Membership of each v in class +1 or – 1 specified by: v An m-by-m diagonal matrix D with +1 & -1 entries v Separate by two bounding planes, v More succinctly: where e is a vector of ones.

Standard Support Vector Machine Formulation v Solve the quadratic program for some min (QP) s. t. where : , denotes or , membership. v Margin is maximized by minimizing

Proximal SVM Formulation (PSVM) Standard SVM formulation: min (QP) s. t. Solving for in terms of and gives: min This simple, but critical modification, changes the nature of the optimization problem tremendously!!

Advantages of New Formulation v Objective function remains strongly convex. v An explicit exact solution can be written in terms of the problem data. v PSVM classifier is obtained by solving a single system of linear equations in the usually small dimensional input space. v Exact leave-one-out-correctness can be obtained in terms of problem data.

Linear PSVM v. We want to solve: min v. Setting the gradient equal to zero, gives a nonsingular system of linear equations. v. Solution of the system gives the desired PSVM classifier.

Linear PSVM Solution Here, v The linear system to solve depends on: which is of size v is usually much smaller than

Linear & Nonlinear PSVM MATLAB Code function [w, gamma] = psvm(A, d, nu) % PSVM: linear and nonlinear classification % INPUT: A, d= diag(D), nu. OUTPUT: w, gamma % [w, gamma] = psvm(A, d, nu); [m, n]=size(A); e=ones(m, 1); H=[A -e]; v=(d’*H)’ %v=H’*D*e; r=(speye(n+1)/nu+H’*H)v % solve (I/ nu+H’*H)r=v w=r(1: n); gamma=r(n+1); % getting w, gamma from r

Numerical experiments One-Billion Two-Class Dataset v Synthetic dataset consisting of 1 billion points in 10 - dimensional input space v Generated by NDC (Normally Distributed Clustered) dataset generator v. Dataset divided into 500 blocks of 2 million points each. v. Solution obtained in less than 2 hours and 26 minutes on a 400 Mhz machine v About 30% of the time was spent reading data from disk. v. Testing set Correctness 90. 79%

Principal Topics v. Knowledge-based classification (NIPS*2002)

Conventional Data-Based SVM

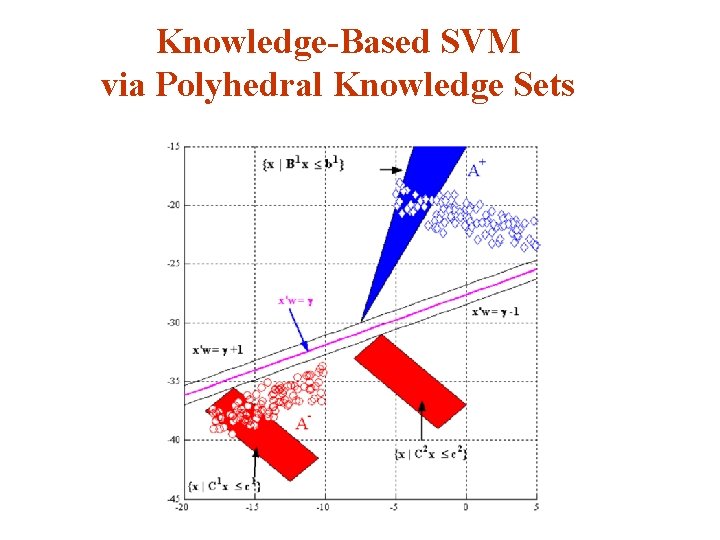
Knowledge-Based SVM via Polyhedral Knowledge Sets

Incoporating Knowledge Sets Into an SVM Classifier v Suppose that the knowledge set: belongs to the class A+. Hence it must lie in the halfspace : v We therefore have the implication: v This implication is equivalent to a set of constraints that can be imposed on the classification problem.

Knowledge Set Equivalence Theorem

Knowledge-Based SVM Classification v Adding one set of constraints for each knowledge set to the 1 -norm SVM LP, we have:

Numerical Testing The Promoter Recognition Dataset v Promoter: Short DNA sequence that precedes a gene sequence. v A promoter consists of 57 consecutive DNA nucleotides belonging to {A, G, C, T}. v Important to distinguish between promoters and nonpromoters v This distinction identifies starting locations of genes in long uncharacterized

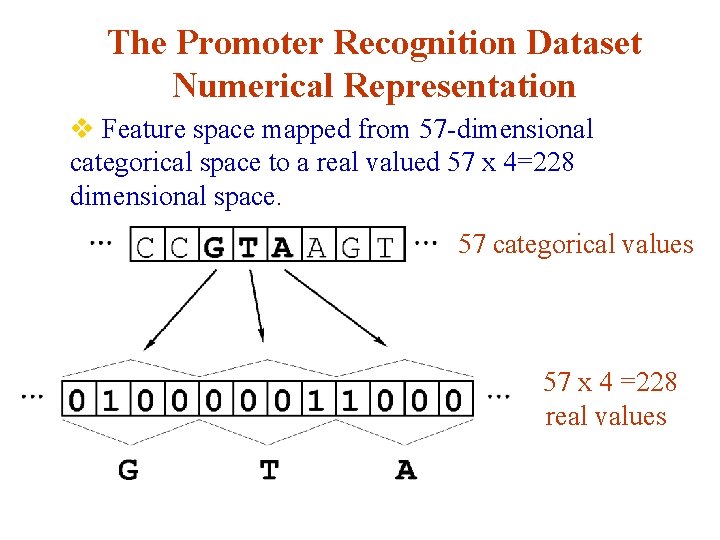
The Promoter Recognition Dataset Numerical Representation v Simple “ 1 of N” mapping scheme for converting nominal attributes into a real valued representation: v Not most economical representation, but commonly

The Promoter Recognition Dataset Numerical Representation v Feature space mapped from 57 -dimensional categorical space to a real valued 57 x 4=228 dimensional space. 57 categorical values 57 x 4 =228 real values

Promoter Recognition Dataset Prior Knowledge Rules v Prior knowledge consist of the following 64 rules:

Promoter Recognition Dataset Sample Rules where denotes position of a nucleotide, with respect to a meaningful reference point starting at position and ending at position Then :

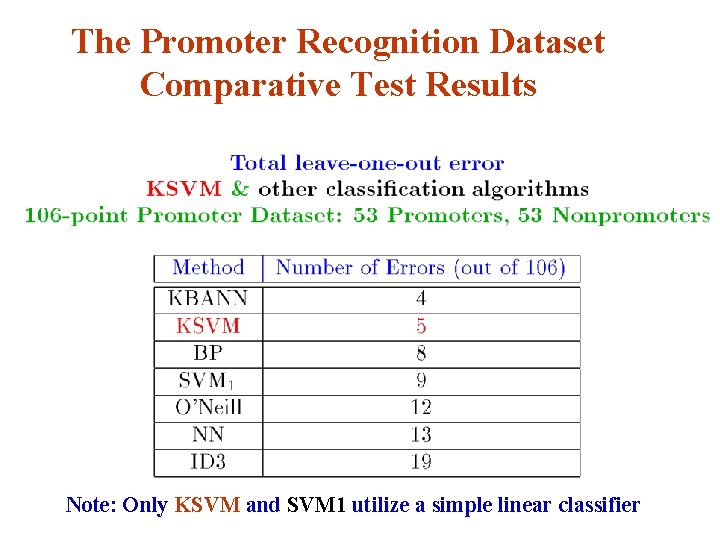
The Promoter Recognition Dataset Comparative Algorithms v KBANN Knowledge-based artificial neural network [Shavlik et al] v BP: Standard back propagation for neural networks [Rumelhart et al] v O’Neill’s Method Empirical method suggested by biologist O’Neill [O’Neill] v NN: Nearest neighbor with k=3 [Cost et al] v ID 3: Quinlan’s decision tree builder [Quinlan] v SVM 1: Standard 1 -norm SVM [Bradley et al]

The Promoter Recognition Dataset Comparative Test Results Note: Only KSVM and SVM 1 utilize a simple linear classifier

Wisconsin Breast Cancer Prognosis Dataset Description of the data v 110 instances corresponding to 41 patients whose cancer had recurred and 69 patients whose cancer had not recurred v 32 numerical features v The domain theory: two simple rules used by doctors:

Wisconsin Breast Cancer Prognosis Dataset Numerical Testing Results v Doctor’s rules applicable to only 32 out of 110 patients. v Only 22 of 32 patients are classified correctly by this rule ( 20% Correctness). v KSVM linear classifier applicable to all patients with correctness of 66. 4%. v Correctness comparable to best available results using conventional SVMs. v KSVM can get classifiers based on knowledge without using any data.

Principal Topics v. Fast Newton method classifier

Fast Newton Algorithm for Classification Standard quadratic programming (QP) formulation of SVM: Once, but not twice differentiable. However Generlized Hessian exists!

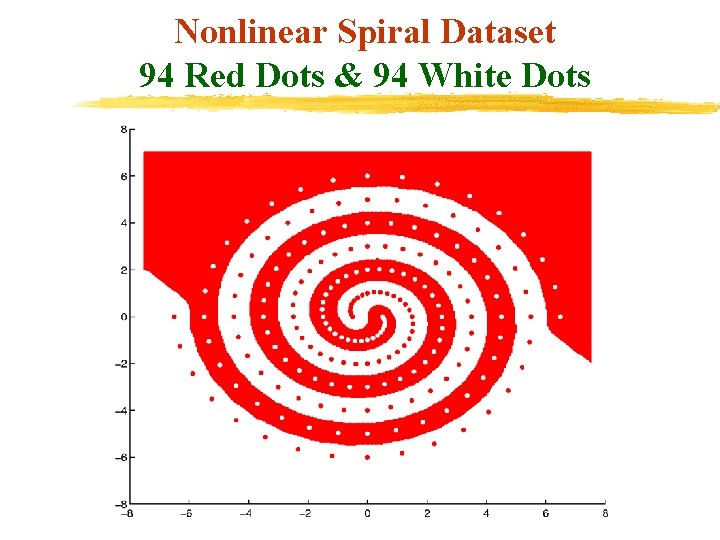
Newton Algorithm v. Newton algorithm terminates in a finite number of steps v. Termination at global minimum v. Error rate decreases linearly v. Can generate complex nonlinear classifiers ØBy using nonlinear kernels: K(x, y)

Nonlinear Spiral Dataset 94 Red Dots & 94 White Dots

Principal Topics v. RSVM: Reduced Support Vector Machines

Difficulties with Nonlinear SVM for Large Problems v The nonlinear kernel Ø Long CPU time to compute is fully dense numbers Ø Runs out of memory while storing kernel matrix v Computational complexity depends on Ø Complexity of nonlinear SSVM v Separating surface depends on almost entire dataset Ø Need to store the entire dataset after solving the problem

Overcoming Computational & Storage Difficulties Use a Rectangular Kernel v Choose a small random sample of Ø The small random sample is a representative of the entire dataset sample is 1% to 10% of the rows of Ø Typically v Replace corresponding by with in nonlinear numbers for Ø Only need to compute and store SSVM the rectangular kernel v Computational complexity reduces to v The nonlinear separator only depends on gives lousy results! Using

Reduced Support Vector Machine Algorithm Nonlinear Separating Surface: (i) Choose a random subset matrix entire data matrix of (ii) Solve the following problem by the Newton : method with corresponding mi n (iii) The separating surface is defined by the optimal in step (ii): solution

How to Choose in RSVM? is a representative sample of the entire dataset Ø Need not be a subset of v A good selection of may generate a classifier using very small v Possible ways to choose : v Ø Choose random rows from the entire dataset Ø Choose such that the distance between its rows exceeds a certain tolerance as Ø Use k cluster centers of and

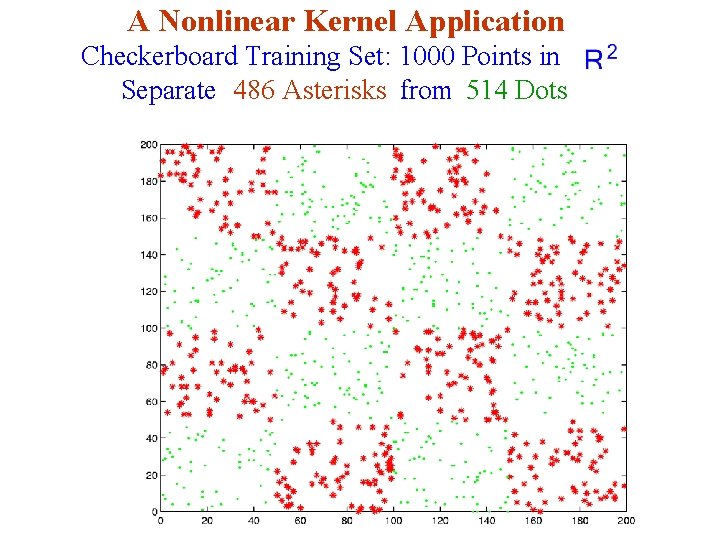
A Nonlinear Kernel Application Checkerboard Training Set: 1000 Points in Separate 486 Asterisks from 514 Dots

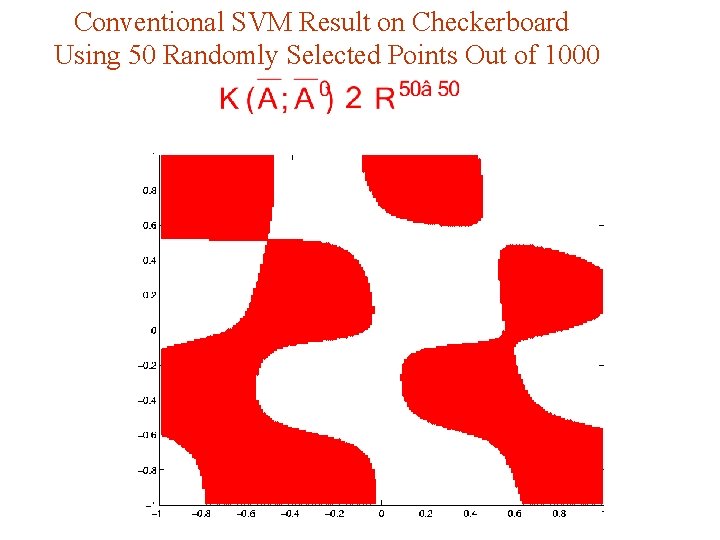
Conventional SVM Result on Checkerboard Using 50 Randomly Selected Points Out of 1000

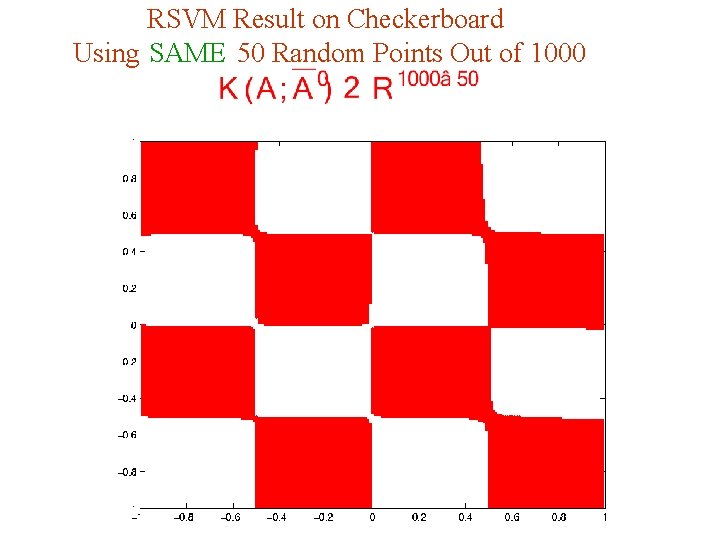
RSVM Result on Checkerboard Using SAME 50 Random Points Out of 1000

Principal Topics v. Breast cancer prognosis & chemotherapy

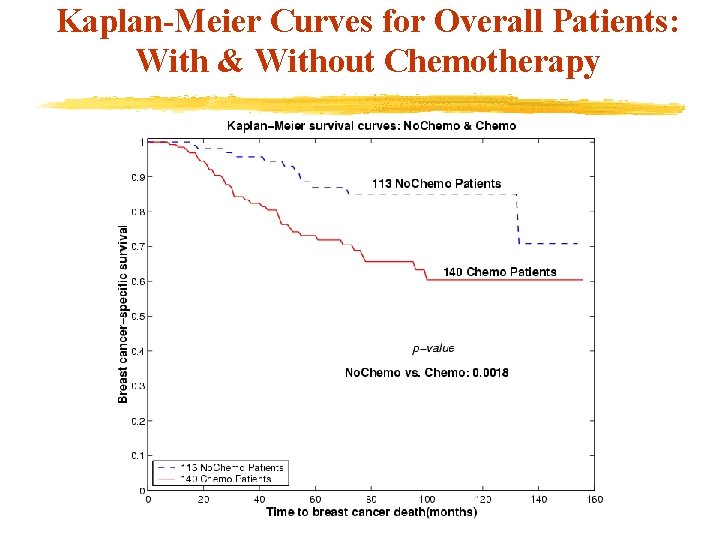
Kaplan-Meier Curves for Overall Patients: With & Without Chemotherapy

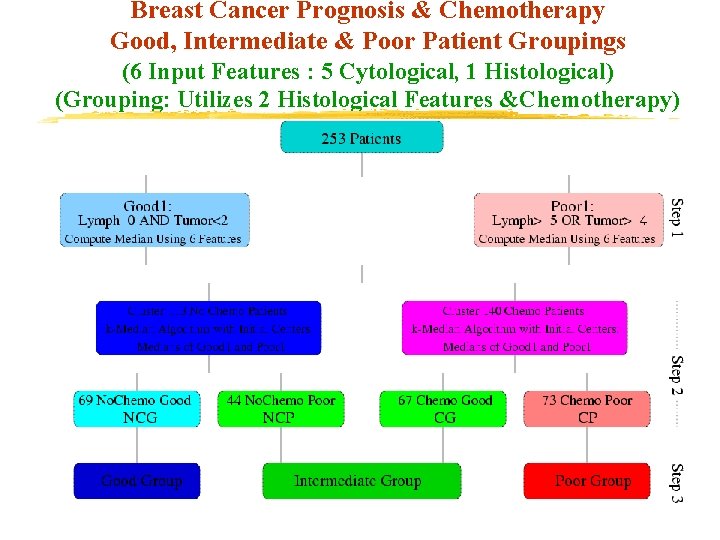
Breast Cancer Prognosis & Chemotherapy Good, Intermediate & Poor Patient Groupings (6 Input Features : 5 Cytological, 1 Histological) (Grouping: Utilizes 2 Histological Features &Chemotherapy)

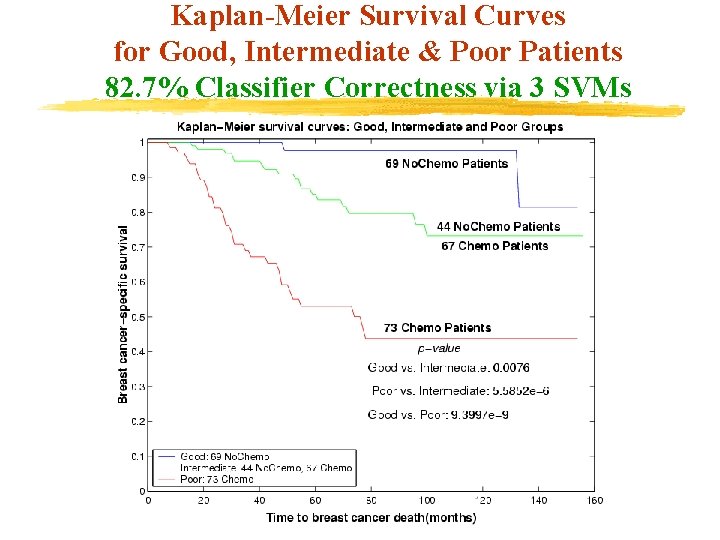
Kaplan-Meier Survival Curves for Good, Intermediate & Poor Patients 82. 7% Classifier Correctness via 3 SVMs

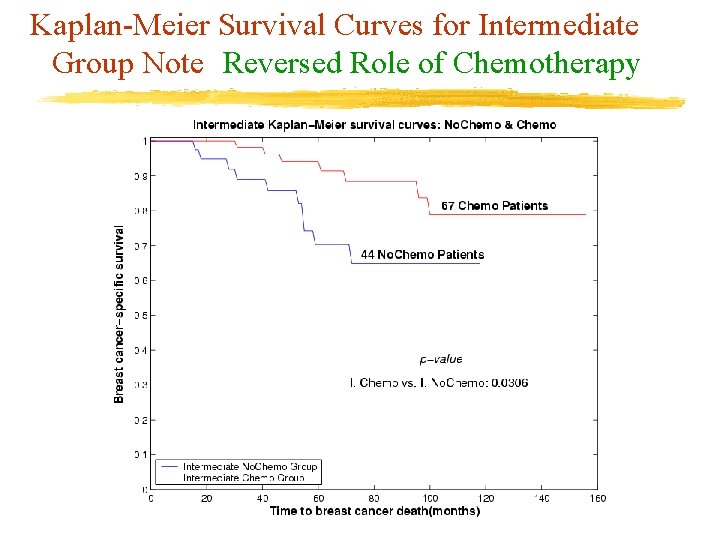
Kaplan-Meier Survival Curves for Intermediate Group Note Reversed Role of Chemotherapy

Conclusion v. New methods for classification v. All based on rigorous mathematical foundation v. Fast computational algorithms capable of classifying massive datasets v. Classifiers based on both abstract prior knowledge as well as conventional datasets v. Identification of breast cancer patients that can benefit from chemotherapy

Future Work v. Extend proposed methods to broader optimization problems Ø Linear & quadratic programming Ø Preliminary results beat state-of-the-art software v. Incorporate abstract concepts into optimization problems as constraints v. Develop fast online algorithms for intrusion and fraud detection v Classify the effectiveness of new drug cocktails in combating various forms of cancer ØEncouraging preliminary results for breast cancer

Breast Cancer Treatment Response Joint with Exon. Hit ( French Bio. Tech) v 35 patients treated by a drug cocktail v 9 partial responders; 26 nonresponders v 25 gene expression measurements made on each patient v 1 -Norm SVM classifier selected: 12 out of 25 genes v. Combinatorially selected 6 genes out of 12 v. Separating plane obtained: 2. 7915 T 11 + 0. 13436 S 24 -1. 0269 U 23 -2. 8108 Z 23 -1. 8668 A 19 -1. 5177 X 05 +2899. 1 = 0. v Leave-one-out-error: 1 out of 35 (97. 1% correctness)

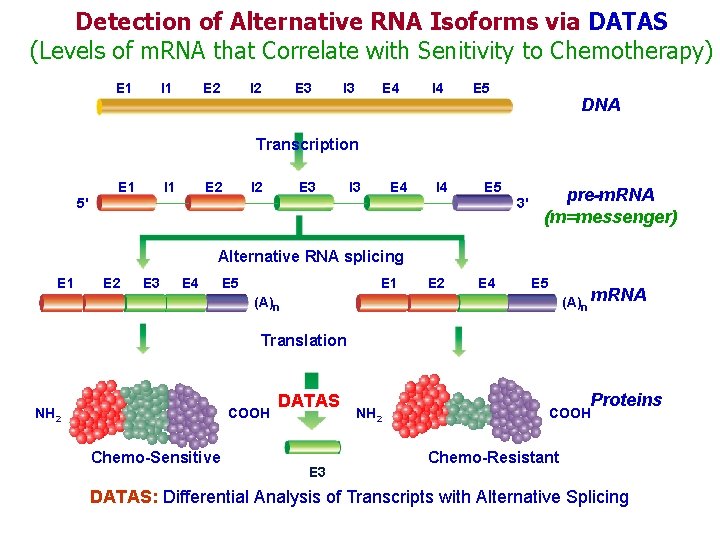
Detection of Alternative RNA Isoforms via DATAS (Levels of m. RNA that Correlate with Senitivity to Chemotherapy) E 1 I 1 E 2 I 2 E 3 I 3 E 4 I 4 E 5 DNA Transcription E 1 I 1 E 2 I 2 E 3 I 3 E 4 I 4 E 5 5' 3' pre-m. RNA (m=messenger) Alternative RNA splicing E 1 E 2 E 3 E 4 E 1 E 5 E 2 E 4 E 5 (A)n m. RNA (A)n Translation NH 2 COOH Chemo-Sensitive DATAS E 3 NH 2 Proteins COOH Chemo-Resistant DATAS: Differential Analysis of Transcripts with Alternative Splicing

Talk Available www. cs. wisc. edu /~olvi