Spieltheorie Andreas Diekmann ETH Zrich Spieltheorie ist wie

Spieltheorie Andreas Diekmann ETH Zürich

►Spieltheorie ist – wie Statistik – ein Gebiet der Mathematik. ► Sie bildet heute die Grundlage der Ökonomie (Kartelle, Auktionsregeln, Regelung von Märkten usw. ). ► Anwendungen finden sich in den Sozialwissenschaften (Soziologie, Sozialpsychologie, Politikwiss. u. a. ), ► in der Informatik (Rechnernetze), ► in der Biologie (evolutionäre Spieltheorie), z. B. reziproker Altruismus unter nicht-verwandten Organismen ► und selbst in der medizinischen Forschung (z. B. Infektion durch Salmonellen, Diard et al. , 2013, Nature 494; Entstehung von Tumoren, Basabta et al. , 2008, Cell Proliferation 41

Roulette: Entscheidung unter Risiko

Was ist Spieltheorie? Im Sinne der Spieltheorie: • Roulette spielen? • Eine Entscheidung für einen Zug im Schach oder bei „Stein, Schere, Papier“ treffen? • Ein Menü auf der Speisekarte auswählen? • Einem Privatpatienten eine einträgliche, aber womöglich wenig nützliche Therapie vorschlagen, dieser ablehnen oder akzeptieren kann?

Was ist Spieltheorie? Im Sinne der Spieltheorie: • Roulette spielen? Kein Spiel • Eine Entscheidung für einen Zug im Schach oder bei „Stein, Schere, Papier“ treffen? Ein Spiel • Ein Menü auf der Speisekarte auswählen? Kein Spiel • Einem Privatpatienten eine Ein Spiel einträgliche, aber womöglich wenig nützliche Therapie vorschlagen, dieser ablehnen oder akzeptieren kann?

Entscheidungen und Spieltheorie 1. Entscheidungen unter Sicherheit oder Risiko (z. B. Roulette): Keine Spieltheorie! 2. Entscheidungsprobleme, bei denen das Ergebnis von den Handlungen anderer Personen abhängt („strategische Interdependenz von Handlungen“) ► Das ist die Domäne der Spieltheorie.

Entscheidungstheorie A. Ein Akteur entscheidet 1. Entscheidungen unter Sicherheit 2. Entscheidungen unter Risiko (z. B. Roulette, Wahrscheinlichkeiten der Konsequenzen sind bekannt). 3. Entscheidungen unter Unsicherheit (die Wahrscheinlichkeiten der Konsequenzen sind nicht bekannt). B. Mehrere Akteure (N ≥ 2) entscheiden und das Ergebnis hängt von der Kombination ihrer Strategien ab. Damit befasst sich die Spieltheorie!

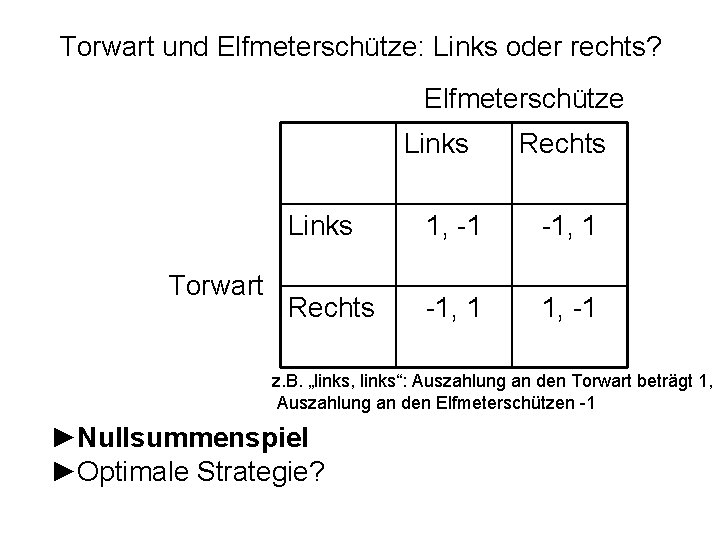
Der unberechenbare Torwart beim Elfmeter • Elfmeterschütze entscheidet: Soll ich den Ball in die linke oder in die rechte Ecke schiessen? • Torwart entscheidet: Soll ich mich nach links oder rechts werfen? Simultane Entscheidung bei hoher Ballgeschwindigkeit und menschlicher Reaktionszeit!

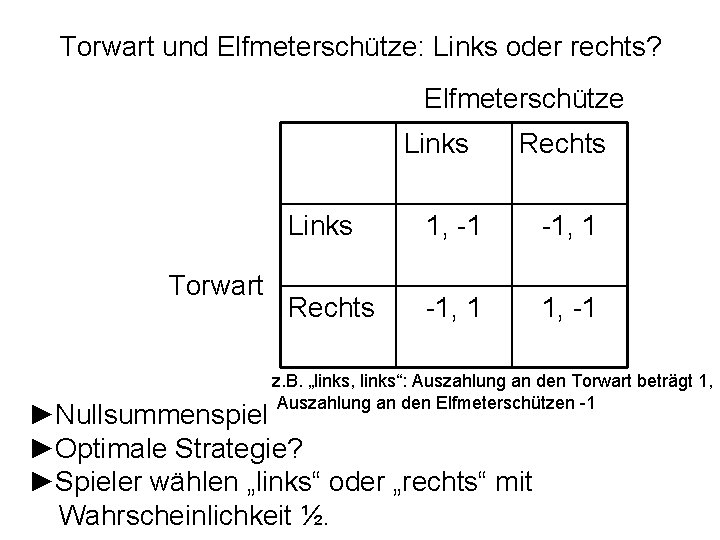
Torwart und Elfmeterschütze: Links oder rechts? Elfmeterschütze Links Torwart Rechts Links 1, -1 -1, 1 Rechts -1, 1 1, -1 z. B. „links, links“: Auszahlung an den Torwart beträgt 1, Auszahlung an den Elfmeterschützen -1 ►Nullsummenspiel ►Optimale Strategie?

Torwart und Elfmeterschütze: Links oder rechts? Elfmeterschütze Links Torwart Rechts Links 1, -1 -1, 1 Rechts -1, 1 1, -1 z. B. „links, links“: Auszahlung an den Torwart beträgt 1, Auszahlung an den Elfmeterschützen -1 ►Nullsummenspiel ►Optimale Strategie? ►Spieler wählen „links“ oder „rechts“ mit Wahrscheinlichkeit ½.

Elfmeter in der dt. Bundesliga Elfmeterschütze Torwart Links Rechts Links 202 (23%) 220 (25%) Rechts 225 (26%) 231 (26%) 878 Elfmeter aus der Spielsaison 92/93 bis 03/04. Nach Berger und Hammer (2007).

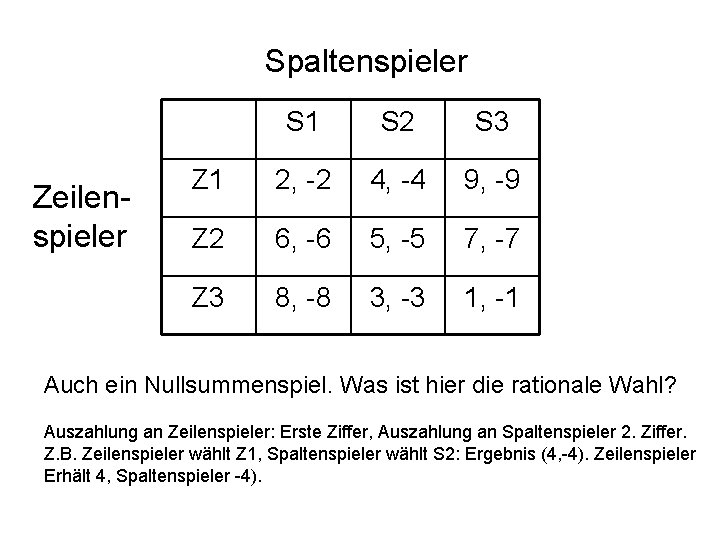
Spaltenspieler Zeilenspieler S 1 S 2 S 3 Z 1 2, -2 4, -4 9, -9 Z 2 6, -6 5, -5 7, -7 Z 3 8, -8 3, -3 1, -1 Auch ein Nullsummenspiel. Was ist hier die rationale Wahl? Auszahlung an Zeilenspieler: Erste Ziffer, Auszahlung an Spaltenspieler 2. Ziffer. Z. B. Zeilenspieler wählt Z 1, Spaltenspieler wählt S 2: Ergebnis (4, -4). Zeilenspieler Erhält 4, Spaltenspieler -4).

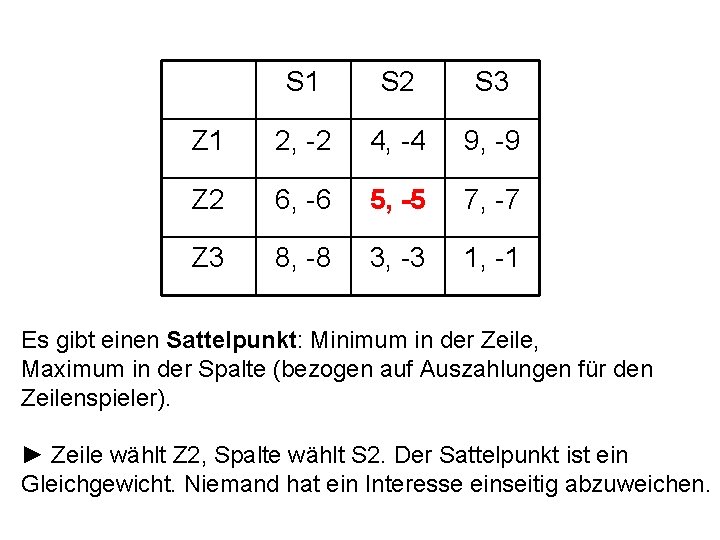
S 1 S 2 S 3 Z 1 2, -2 4, -4 9, -9 Z 2 6, -6 5, -5 7, -7 Z 3 8, -8 3, -3 1, -1 Es gibt einen Sattelpunkt: Minimum in der Zeile, Maximum in der Spalte (bezogen auf Auszahlungen für den Zeilenspieler). ► Zeile wählt Z 2, Spalte wählt S 2. Der Sattelpunkt ist ein Gleichgewicht. Niemand hat ein Interesse einseitig abzuweichen.

Sattelpunkt-Theorem Minimum in der Zeile, Maximum in der Spalte

„The Final Problem“ (1893): Sherlock Holmes und Professor Moriarty Kent railways Wikipedia London Victoria ►Canterbury ►Dover ► Holmes überlegt: Soll ich den Zug in Canterbury verlassen? Aber damit rechnet Reichenbachfälle, auch Moriarty. Also doch besser bis Dover? Meiringen Aber das kalkuliert Moriarty auch ein – dann doch in Dover aussteigen? usw. … Welche ist die rationale Strategie von Holmes, von Moriarty?

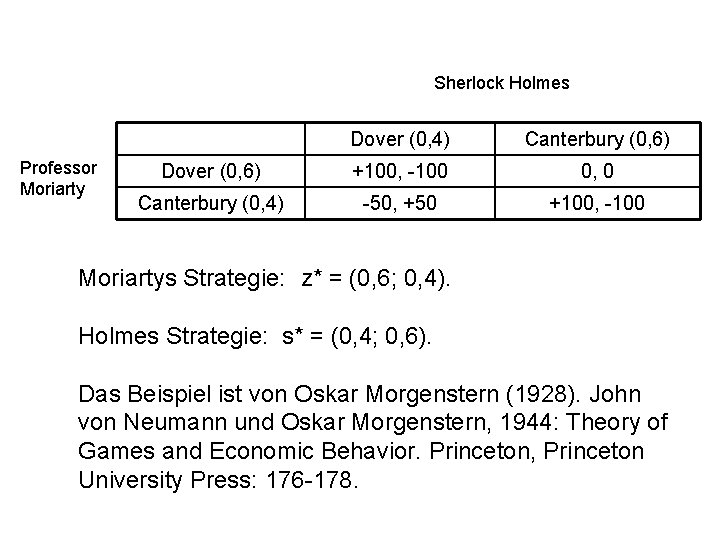
Sherlock Holmes Professor Moriarty Dover (0, 4) Canterbury (0, 6) Dover (0, 6) +100, -100 0, 0 Canterbury (0, 4) -50, +50 +100, -100 Moriartys Strategie: z* = (0, 6; 0, 4). Holmes Strategie: s* = (0, 4; 0, 6). Das Beispiel ist von Oskar Morgenstern (1928). John von Neumann und Oskar Morgenstern, 1944: Theory of Games and Economic Behavior. Princeton, Princeton University Press: 176 -178.

John von Neumann (1928) Einer der genialsten Mathematiker des 20. Jahrhunderts hat sich vorwiegend mit Nullsummenspielen befasst. John von Neumann, 1928: Theorie der Gesellschaftsspiele. Mathematische Annalen 100: 295 -320

John von Neumann (1928) Minimax-Theorem. Jedes Nullsummenspiel mit endlicher Anzahl Strategien hat ein Gleichgewicht in reinen oder gemischten Strategien (John von Neumann, 1928: Theorie der Gesellschaftsspiele)

Warum hat John von Neumann die Spieltheorie entwickelt?

Warum hat John von Neumann die Spieltheorie entwickelt? 1. Er war begeisterter Poker-Spieler und wollte Poker auf eine rationale Grundlage stellen.

Warum hat John von Neumann die Spieltheorie entwickelt? 1. Er war begeisterter Poker-Spieler und wollte Poker auf eine rationale Grundlage stellen. 2. Er wollte „Kontroversen“ mit seiner Frau „rational“ lösen.

Warum hat John von Neumann die Spieltheorie entwickelt? 1. Er war begeisterter Poker-Spieler und wollte Poker auf eine rationale Grundlage stellen. 2. Er wollte „Kontroversen“ mit seiner Frau „rational“ lösen. 3. Frau von Neumann soll gesagt haben, sie interessiere sich nur für Spieltheorie, wenn darin ein Elefant vorkäme.

John von Neumann und Oskar Morgenstern, 1947: Theory of Games and Economic Behavior. Princeton, Princeton University Press: 64 (2. Aufl. )

• Nullsummenspiele: Vollständig antagonistische Interessen, keine Möglichkeit zur Kooperation • Die Welt ist „Nonzero“ (Robert Wright). Dieses Buch zur Spieltheorie wurde von einem Mitspieler in der Weltpolitik empfohlen, nämlich von Bill Clinton auf youtube („Last year I read a book that describes the way the world works. “) http: //www. youtube. com/watch? v=Dn. Los. ZVG 54 k • Die meisten Konfliktsituationen entsprechen Spielen mit gemischten Interessen. Die Akteure haben teils gemeinsame, teils divergierende Interessen.

Nicht-Nullsummenspiele Eines der bekanntesten Spiele: Gefangenendilemma Eine Parabel für den Konflikt zwischen individuellen Interessen und kollektivem Gut Besuchen Sie „Tosca“ und entdecken Sie ein Gefangenendilemma zwischen Tosca und Scarpia!

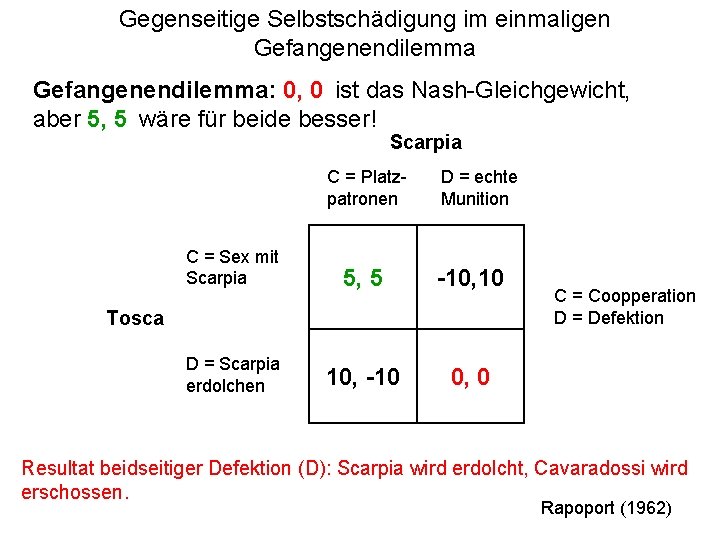
Gegenseitige Selbstschädigung im einmaligen Gefangenendilemma: 0, 0 ist das Nash-Gleichgewicht, aber 5, 5 wäre für beide besser! Scarpia C = Platzpatronen D = echte Munition C = Sex mit Scarpia 5, 5 -10, 10 D = Scarpia erdolchen 10, -10 0, 0 Tosca C = Coopperation D = Defektion Resultat beidseitiger Defektion (D): Scarpia wird erdolcht, Cavaradossi wird erschossen. Rapoport (1962)

John F. Nash (1950, 1951) “Nash-Gleichgewicht” Jedes Spiel mit endlicher Anzahl von Strategien hat mindestens ein Gleichgewicht in reinen oder gemischten Strategien. Nash, John F. (1950): Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, USA, 36: 48 -49. Nash, John F. (1951): Non-cooperative games. Annals of Mathematics 54: 286295. Nobelpreis zusammen mit J. Harsanyi und R. Selten 1994 „Beautiful Mind“

Evolution von Kooperation In the state of nature life was „solitary, poor, nasty, brutish, and short“ (Thomas Hobbes 1651) Kooperieren Betrügen 5, 5 -10, 10 10, -10 0, 0

Evolution von Kooperation unter Egoisten Kann dennoch unter Egoisten ohne äußere Sanktionen (“ohne Leviathan, ohne Staat”) Kooperation entstehen? Wird das Gefangenendilemma (die Interaktion) wiederholt, ohne das Ende der Interaktionen bekannt ist und sind die künftigen Erträge hoch genug, dann ändert sich die strategische Situation grundlegend.

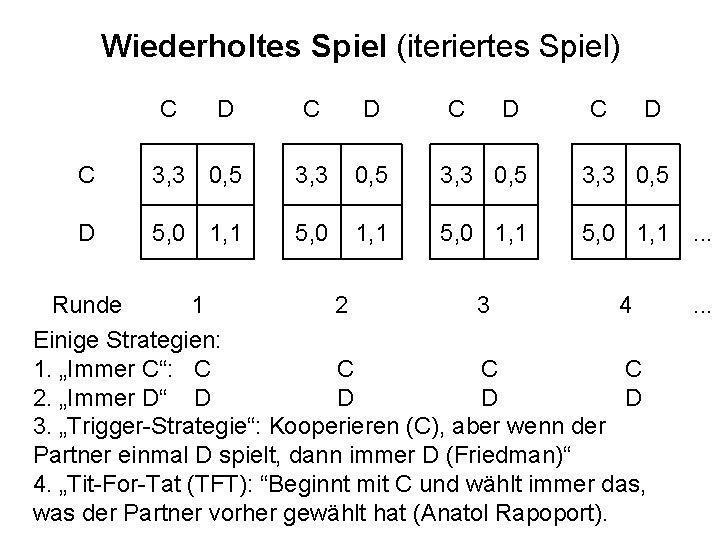
Wiederholtes Spiel (iteriertes Spiel) C D C D C 3, 3 0, 5 D 5, 0 1, 1. . . Runde 1 2 3 4 Einige Strategien: 1. „Immer C“: C C 2. „Immer D“ D D 3. „Trigger-Strategie“: Kooperieren (C), aber wenn der Partner einmal D spielt, dann immer D (Friedman)“ 4. „Tit-For-Tat (TFT): “Beginnt mit C und wählt immer das, was der Partner vorher gewählt hat (Anatol Rapoport). .

Evolution von Kooperation unter Egoisten Kann dennoch unter Egoisten ohne äußere Sanktionen (“ohne Leviathan, ohne Staat”) Kooperation entstehen? Wird das Gefangenendilemma (die Interaktion) wiederholt, ohne dass das Ende der Interaktionen bekannt ist und sind die künftigen Erträge hoch genug, dann werden beide Akteure dauerhaft kooperieren. Beispiel: Sozialer Austausch. Voraussetzung: Wiederholtes Spiel und hinreichend großer “Schatten der Zukunft” Computersimulationen von Axelrod (1984): “Tit-for-Tat” als Gewinnstrategie (Anatol Rapoport)

Stellungskrieg im I. Weltkrieg System des “Leben und leben lassen”

Aus Tagebuchaufzeichnungen von Weltkrieg I Soldaten: „Der kleine Friede im großen Krieg“ (Michael Jürgs): Kooperation unter feindlichen Soldaten Im Stellungskrieg an der Westfront „Der wahre Grund, dass es in einigen Abschnitten so ruhig war, bestand darin, dass keine Seite die Absicht hatte, in das Gebiet vorzurücken. … Wenn die Briten die Deutschen mit Granaten beschossen, reagierten die Deutschen und das Ausmaß der Zerstörung war auf beiden Seiten gleich. Wenn die Deutschen den vorderen Teil des Schützengrabens bombardierten und fünf Engländer töteten, wurde zurück gefeuert und fünf Deutsche getötet“ (Belton Cobb 1916). „In einem Abschnitt wurde die Zeit von 8 bis 9 am Morgen „privaten Geschäften“ gewidmet, und gewisse Plätze, die durch eine rote Fahne markiert waren, waren für die Scharfschützen beider Seiten Tabu“ (Morgan 1916). „Ich trank Tee mit der Kompanie als wir Rufe hörten und hinausgingen um nachzuschauen. Wir sahen unsere Leute und die Deutschen auf den Schützengräben. Plötzlich kam eine Salve, richtete aber keinen Schaden an. Natürlich gingen beide Seiten in Deckung und unsere Männer begannen auf die Deutschen zu fluchen, als plötzlich ein mutiger Deutscher auf die Brüstung stieg und rief: ‚Es tut uns sehr Leid, dass dies passierte. Wir hoffen, niemand wurde verletzt. Es ist nicht unsere Schuld, es ist die verdammte preußische Artillerie!“ (Rutter 1934). (Zitate aus Ashworth 1980 in Axelrod 1984)

Der brave Mann denkt an sich selbst zuletzt!

Der brave Mann denkt an sich, selbst zuletzt! Fairness und (begrenzter) Altruismus oder homo oeconomicus?

Nicht nur Eigennutz: Diktator- und Ultimatumspiel • Ultimatumspiel: Eine Person teilt den Kuchen (z. B. 100 Fr. ) auf. Der Mitspieler hat aber ein Vetorecht. Lehnt er ab, gehen beide leer aus. ► Rationalitätstheorie: Spieler 1 bietet den kleinstmöglichen Betrag an (1 Rp. ), Spieler 2 wird akzeptieren. ►In Experimenten dagegen: Fairness und „altruistische Reziprozität“ (im Ultimatumspiel selbstschädigende Reziprozität) ►Zahlreiche Anwendungen: Z. B. Erklärung für Stabilität von Normen, Kooperation in Teams, Effizienzlohntheorie und Erklärung von Arbeitslosigkeit u. a.

Kommt dem Nash. Gleichgewicht nahe! Rheinpfalz, 12. 9. 02

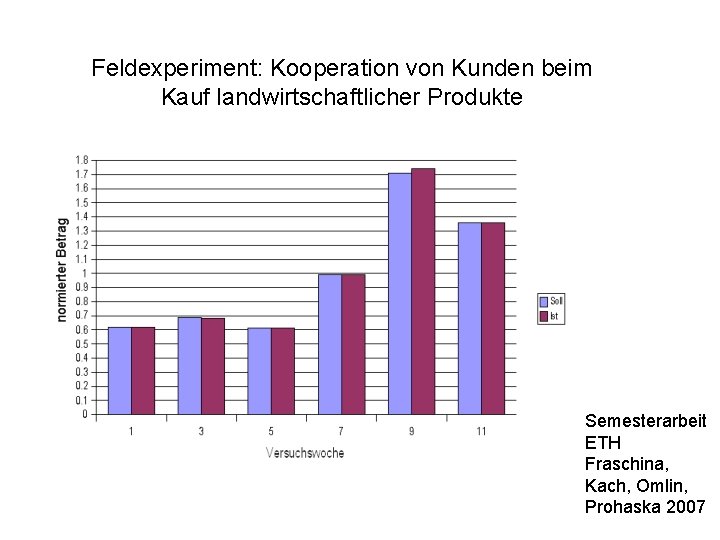
Feldexperiment Kooperation Verkauf von Honig und anderen landwirtschaftlichen Erzeugnissen an einem Selbstbedienungsstand in der Region Luzern. Kunden legen den Kaufpreis in eine Kasse. Es gibt keine Überwachung. Semester paper at ETH Fraschina, Kach, Omlin, Prohaska 2007

Feldexperiment: Kooperation von Kunden beim Kauf landwirtschaftlicher Produkte Semesterarbeit ETH Fraschina, Kach, Omlin, Prohaska 2007

“Friend or Foe” Variante eines “Gefangenendilemma” in TV-Sendung Friend (Split) Foe (Steal) Friend (Split) 1000, 1000 0, 2000 Foe (Steal) 2000, 0 Golden Ball: „Split“ or „steal“ in UK TV-Show

“Friend or Foe” Variante von “Gefangenendilemma” in TV-Sendung. List (2006): Auswertung für 234 Spieler der Show in den USA. Steve Friend (Split) Sarah Foe (Steal) Ergebnis: Friend (Split) 50075 £, 50075 £ 0, 100150 £ Kooperation 50 % Foe (Steal) 100150 £, 0 0, 0 Männer 45 % Frauen 56 % Drei Gleichgewichte – Grenzfall von GD und Chicken!

Wem vertrauen Sie? Partnersuche, Versicherungsnehmer, Einstellung von Mitarbeitern, Kreditnehmer. Signale des Vertrauens! ►Asymmetrische Information und Signalspiele In den USA geben Männer etwa drei Monatseinkommen aus für Verlobungsringe.

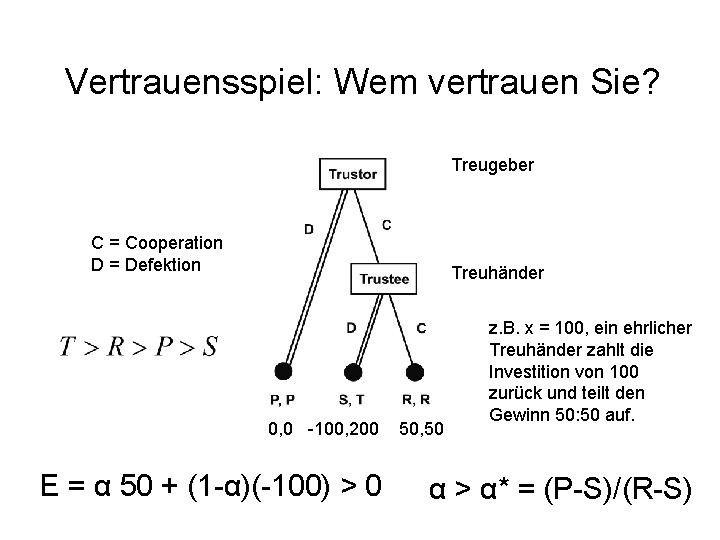
Vertrauensspiel: Wem vertrauen Sie? Treugeber C = Cooperation D = Defektion Treuhänder 0, 0 -100, 200 E = α 50 + (1 -α)(-100) > 0 50, 50 z. B. x = 100, ein ehrlicher Treuhänder zahlt die Investition von 100 zurück und teilt den Gewinn 50: 50 auf. α > α* = (P-S)/(R-S)

Soziale Dilemmata • Ähnlich Gefangenendilemma, aber auch mehr als zwei Akteure • Selbstzerstörerische Konkurrenz, Rüstungswettlauf • Beitrag zu kollektiven Gütern: Z. B. 80 % der Deutschen befürworten Organtransplantationen, aber nur 12 % haben einen Spenderausweis (“Trittbrettfahrerproblem”). • Umweltprobleme, Übernutzung knapper Ressourcen

Shubik (1971): 1 -$-Auktion „Englische“ Auktion: Offen, ansteigend, das höchste Gebot gewinnt. Nur eine Ausnahme: Der zweithöchste Bieter muss ebenfalls für sein Gebot zahlen, erhält aber nicht die Ware.

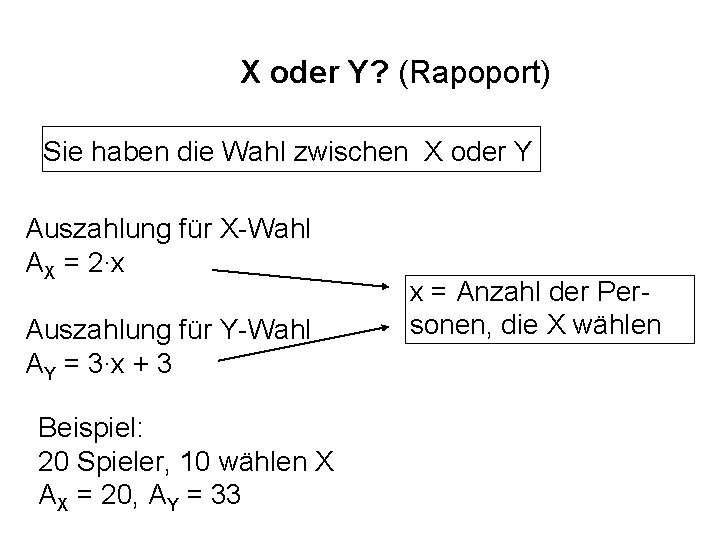
X oder Y? (Rapoport) Sie haben die Wahl zwischen X oder Y Auszahlung für X-Wahl AX = 2∙x Auszahlung für Y-Wahl AY = 3∙x + 3 Beispiel: 20 Spieler, 10 wählen X AX = 20, AY = 33 x = Anzahl der Personen, die X wählen

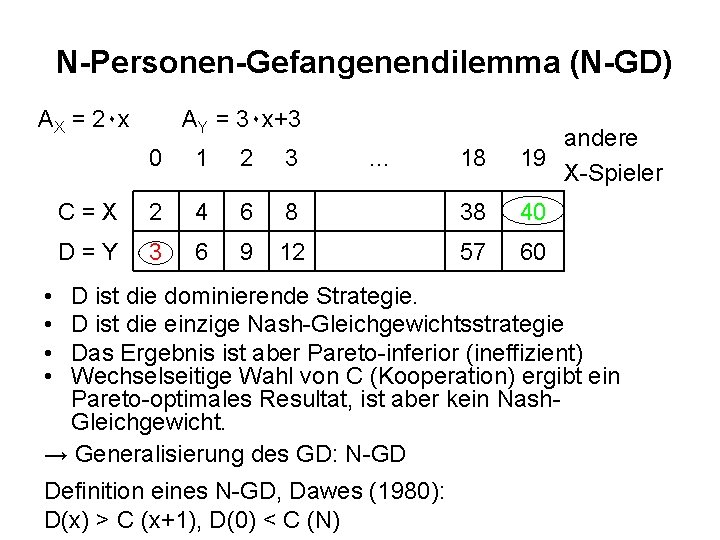
N-Personen-Gefangenendilemma (N-GD) AX = 2۰ x AY = 3۰ x+3 18 andere 19 X-Spieler 8 38 40 12 57 60 0 1 2 3 C=X 2 4 6 D=Y 3 6 9 … • • D ist die dominierende Strategie. D ist die einzige Nash-Gleichgewichtsstrategie Das Ergebnis ist aber Pareto-inferior (ineffizient) Wechselseitige Wahl von C (Kooperation) ergibt ein Pareto-optimales Resultat, ist aber kein Nash. Gleichgewicht. → Generalisierung des GD: N-GD Definition eines N-GD, Dawes (1980): D(x) > C (x+1), D(0) < C (N)

Die höchste Zahl gewinnt! • Schreiben Sie eine ganze Zahl ≥ 1 auf einen Zettel • Die höchste Zahl gewinnt. Allerdings wird der Preis durch die Gewinnzahl geteilt. • Schreiben mehrere Teilnehmer die höchste Zahl auf, wird der Gewinn unter ihnen gleich aufgeteilt. • Der Preis beträgt 100 Fr. und wird von mir ausgezahlt!

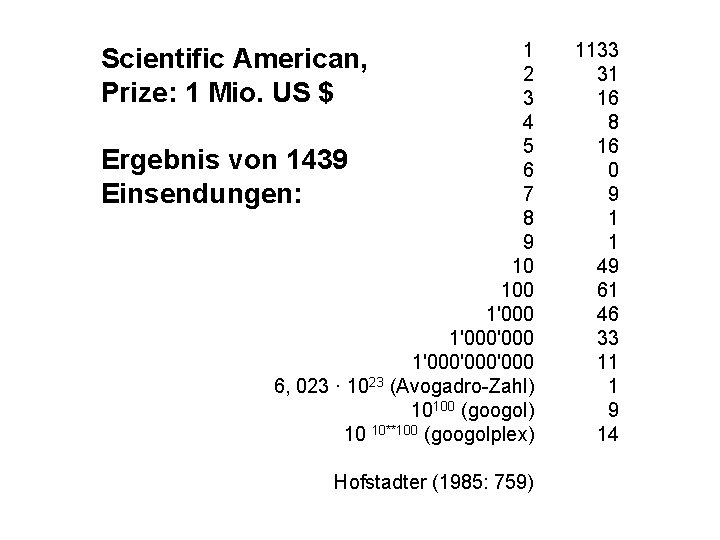
1 2 3 4 5 Ergebnis von 1439 6 7 Einsendungen: 8 9 10 100 1'000'000 6, 023 · 1023 (Avogadro-Zahl) 10100 (googol) 10 10**100 (googolplex) Scientific American, Prize: 1 Mio. US $ Hofstadter (1985: 759) 1133 31 16 8 16 0 9 1 1 49 61 46 33 11 1 9 14

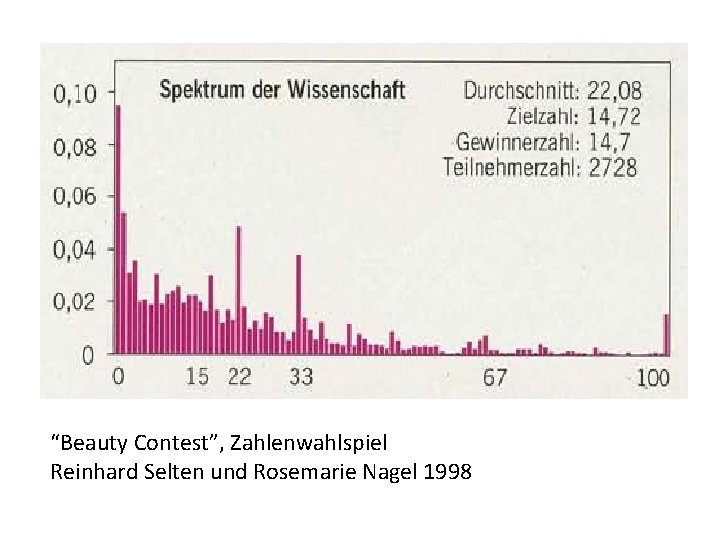
“Beauty Contest”, Aktienblasen und rationales Handeln Soll man rational handeln, wenn man weiss, die anderen handeln irrational? Sie können eine Zahl zwischen 0 und 100 wählen. Auch alle anderen Personen sind in der gleichen Situation und sollen unabhängig voneinander eine Zahl in diesem Bereich wählen. Sie gewinnen 1 Mio €, wenn Sie 2/3 des Mittelwerts aller gewählten Zahlen am nächsten kommen. Bei mehreren Gewinnern wird der Preis geteilt! Die rationale Wahl, die Nash-Gleichgewichtsstrategie, ist?

“Beauty Contest”, Zahlenwahlspiel Reinhard Selten und Rosemarie Nagel 1998

Holländische Tulpenmanie 1637 Herbst 1636 60 15. Jan. 1637 120 23. Jan. 1637 385 1. Feb. 1637 1200 3. Feb. 1637 1500 Nach dem Crash (nach 3. 2. ) ca. 70 Sorte „Semper Augustus“ Preise auf Tulpenauktionen in Gulden für ein Pfund der (relativ billigen) Sorte „Switsers“. Zum Vergleich: Preis eines „fetten Ochsen“ 120 Gulden. Aus Mike Dash, 1999.

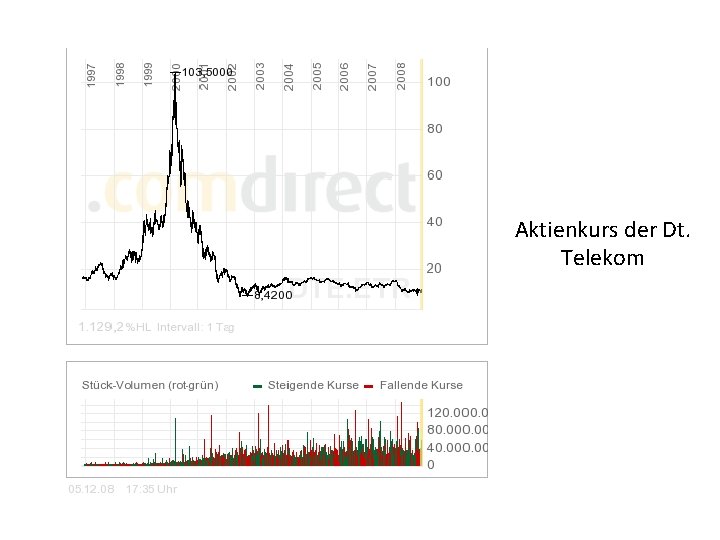
Aktienkurs der Dt. Telekom

Das Allmende-Dilemma Eine Gruppe von 10 Personen besucht ein Restaurant. Sie beschliessen, die Rechnung durch die Zahl der Köpfe zu teilen. Weniger zivilisierte Personen werden einen grösseren Appetit als bei individueller Abrechnung entwickeln. 9/10 der Rechnung wird von den anderen Tischgenossen subventioniert. Folgen alle Gäste dieser Logik, wird die Rechnung zum Schaden aller aufgebläht. Gleiche Logik in einem Mietshaus mit gemeinsamer Heizkostenabrechnung. Die Abholzung von Wäldern, die Überfischung der Meere und allgemein die Übernutzung von Ressourcen sind Beispiele mit gravierenderen Konsequenzen.

Die klugen Bauern von Törbel im Wallis ► Klug eingerichtete Institutionen lösen soziale Dilemmata!

Fallstudie: Törbel, Schweiz Allmendenutzung 1. Zugangsregelung: N Teilnehmer 2. Begrenzung der Ressourcennutzung. “Winterregel”: Nur soviel Vieh darf auf die Allmende, wie im Winter aus eigenem Anbau versorgt werden kann. 3. “Gewalthaber” verhängt Sanktionen bei Regelverstössen und erhält 50 % der Busse. Elinor Ostrom 1990, Nobelpreis 2009 für die Untersuchung von Allmenden („Die Verfassung der Allmende“)

► Institutionen sind Lösungen für soziale Dilemmata ► Analyse und Design von Institutionen (z. B. Reputation auf Märkten (e. Bay), Sanktionsmechanismen, Allmendedilemma, Auktionsregeln, Emissionszertifikate, Ratingagenturen, Kartellrecht, Verkehrssteuerung etc. : Spieltheorie analysiert und entwickelt Lösungsvorschläge.

► Institutionen sind Lösungen für soziale Dilemmata ► Analyse und Design von Institutionen (z. B. Reputation auf Märkten (e. Bay), Sanktionsmechanismen, Allmendedilemma, Auktionsregeln, Emissionszertifikate, Ratingagenturen, Kartellrecht, Verkehrssteuerung etc. : Spieltheorie analysiert und entwickelt Lösungsvorschläge. ► Leider haben die Verhandlungen über die globale Allmende (Klimawandel) bislang nicht zu ähnlich weisen Regeln geführt, wie sie in Törbel Jahrhunderte existierte haben.

Klug geplante Institutionen zahlen sich aus! ►Ken Binmore hat mit seinem Team die Regeln zur Versteigerung der Mobilfunkfrequenzen in Grossbritannien auf Grundlage der Spieltheorie entwickelt. Die Einnahmen betrugen 22, 5 Milliarden Pfund Sterling (38, 5 Milliarden US $). ►Die kurz danach (2000) durchgeführte Auktion in der Schweiz war ein Desaster. Die Eidgenossenschaft erzielte für vier Lizenzen magere 205 Mio Fr. ►Für den Schweizer Steuerzahler hätte es sich gelohnt, den Spieltheoretiker Binmore als Berater anzuheuern.

Wenn Sie etwas mehr wissen möchten … diekmann@soz. gess. ethz. ch

THE END