Some things are easier to heat Can you




















































- Slides: 80

Some things are easier to heat Can you think of examples? • More water in the pot needs longer time to boil • Alcohol/saltwater needs less energy to heat it than water • Transfer of energy (Q - heat) is proportional to the change in temperature (DT) x mass (m) of material x C How to calculate C? Q = m C(T) DT • C called the specific heat of a material – Cwater = 4190 J/(kg K) - very difficult to heat – Cice = 2090 J/(kg K) – Cmercury = 138 J/(kg K) - very easy to heat (thermometers) –C = 2428 J/(kg K) – much easier than water

Lattice Vibrational Contribution to the Heat Capacity The thermal energy is the dominant contribution to the heat capacity in most solids. In non-magnetic insulators, it is the only contribution.

Lattice Vibrational Contribution to the Heat Capacity The thermal energy is the dominant contribution to the heat capacity in most solids. In non-magnetic insulators, it is the only contribution. Some other contributions: Conduction Electrons in metals & semiconductors (will discuss later).

Lattice Vibrational Contribution to the Heat Capacity The thermal energy is the dominant contribution to the heat capacity in most solids. In non-magnetic insulators, it is the only contribution. Some other contributions: Conduction Electrons in metals & semiconductors (will discuss later). The magnetic ordering in magnetic materials.

First Classical Theory of Heat Capacity (too simple, but a good start) When the solid is heated, the atoms vibrate around their sites like harmonic oscillators.

First Classical Theory of Heat Capacity (too simple, but a good start) When the solid is heated, the atoms vibrate around their sites like harmonic oscillators. The average energy for a 1 D oscillator is ½ k. BT. (Boltzmann const. )

First Classical Theory of Heat Capacity (too simple, but a good start) When the solid is heated, the atoms vibrate around their sites like harmonic oscillators. The average energy for a 1 D oscillator is ½ k. BT. (Boltzmann const. ) Therefore, the average energy per atom, regarded as a 3 D oscillator, is 3/2 k. BT, and consequently the total energy is 3/2 Nk. BT where N is the number of atoms.

First Classical Theory of Heat Capacity (too simple, but a good start) When the solid is heated, the atoms vibrate around their sites like harmonic oscillators. The average energy for a 1 D oscillator is ½ k. BT. (Boltzmann const. ) Therefore, the average energy per atom, regarded as a 3 D oscillator, is 3/2 k. BT, and consequently the total energy is 3/2 Nk. BT where N is the number of atoms. Differentiation w. r. t temperature gives heat capacity of 3/2 N k. B (predicts energy/atom is constant)

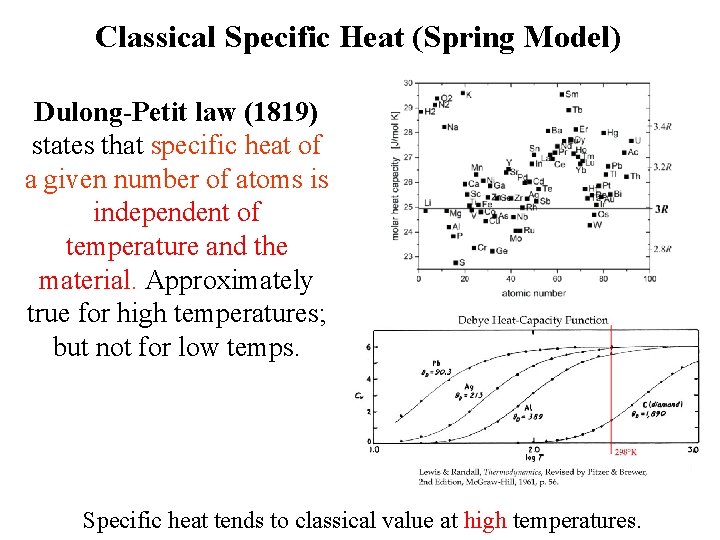
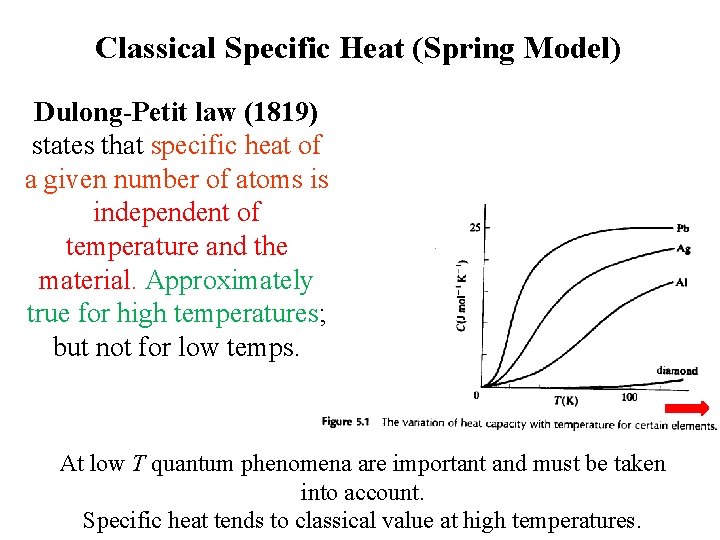
Classical Specific Heat (Spring Model) Dulong-Petit law (1819) states that specific heat of a given number of atoms is independent of temperature and the material. Approximately true for high temperatures; but not for low temps. Specific heat tends to classical value at high temperatures.

Classical Specific Heat (Spring Model) Dulong-Petit law (1819) states that specific heat of a given number of atoms is independent of temperature and the material. Approximately true for high temperatures; but not for low temps. At low T quantum phenomena are important and must be taken into account. Specific heat tends to classical value at high temperatures.

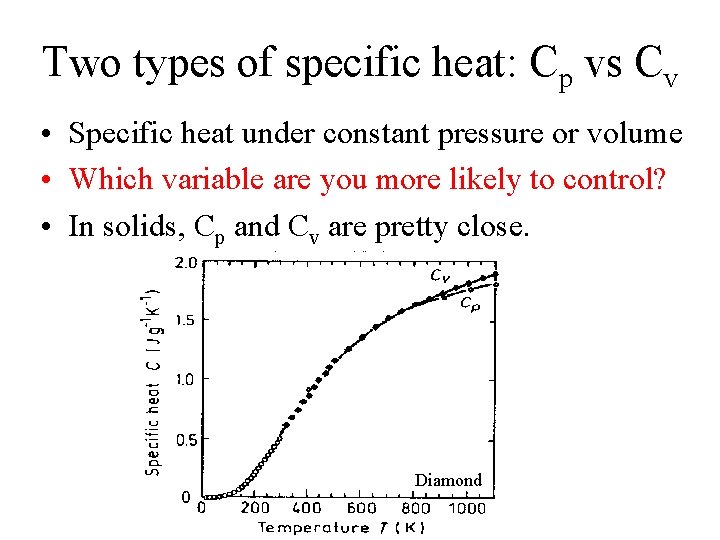
Two types of specific heat: Cp vs Cv • Specific heat under constant pressure or volume

Two types of specific heat: Cp vs Cv • Specific heat under constant pressure or volume • Which variable are you more likely to control?

Two types of specific heat: Cp vs Cv • Specific heat under constant pressure or volume • Which variable are you more likely to control? • In solids, Cp and Cv are pretty close. Diamond

To be thorough need to find the total energy of the phonons U, then take d. U/d. T to find C. How to find U?

To be thorough need to find the total energy of the phonons U, then take d. U/d. T to find C. How to find U?

To be thorough need to find the total energy of the phonons U, then take d. U/d. T to find C. How to find U? Let’s learn how to get these!

Thermal Energy & Heat Capacity Quantum Model According to Quantum Mechanics if a particle is constrained; • the energy of the particle can only have special discrete energy values. • it cannot increase infinitely from one value to another. • it has to go up in steps (here: steps of the phonon energy)

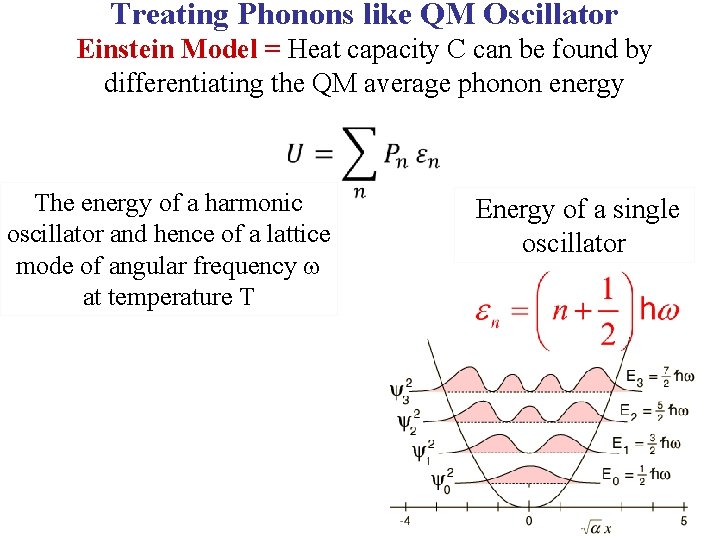
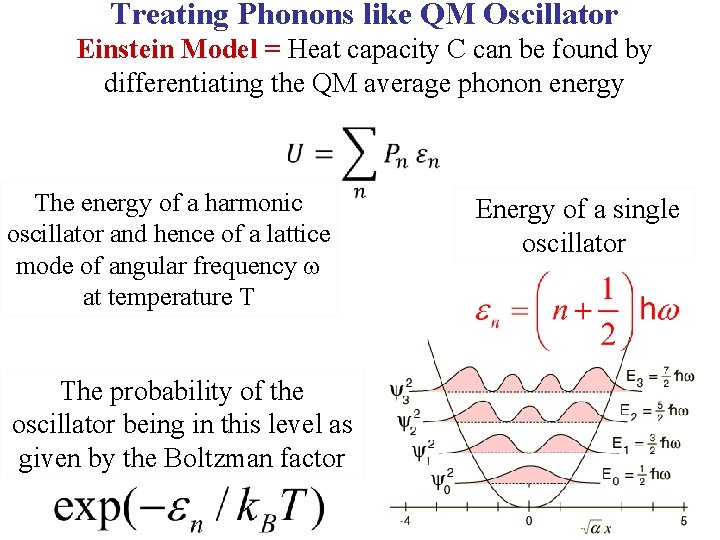
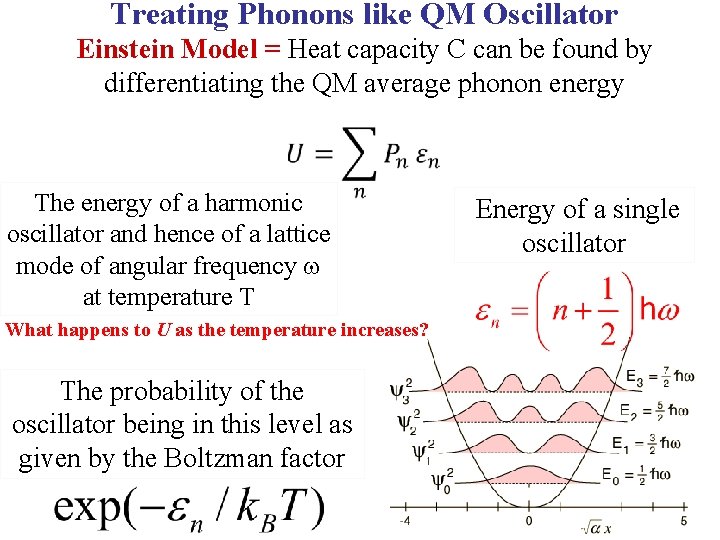
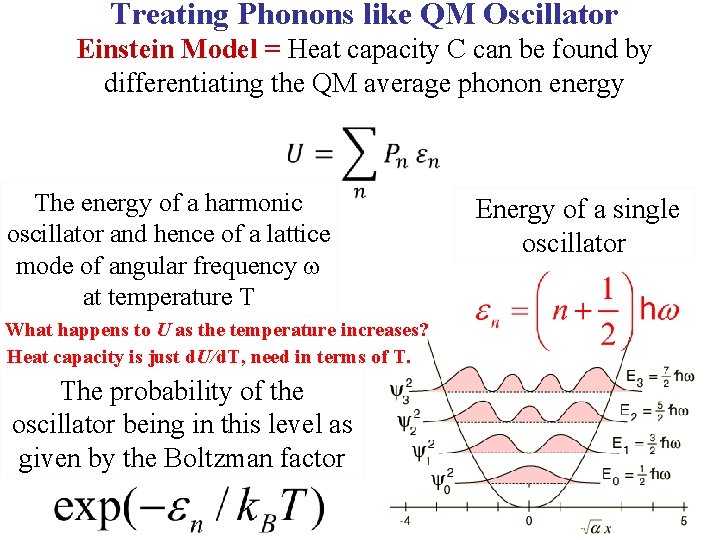
Treating Phonons like QM Oscillator Einstein Model = Heat capacity C can be found by differentiating the QM average phonon energy

Treating Phonons like QM Oscillator Einstein Model = Heat capacity C can be found by differentiating the QM average phonon energy The energy of a harmonic oscillator and hence of a lattice mode of angular frequency at temperature T Energy of a single oscillator

Treating Phonons like QM Oscillator Einstein Model = Heat capacity C can be found by differentiating the QM average phonon energy The energy of a harmonic oscillator and hence of a lattice mode of angular frequency at temperature T The probability of the oscillator being in this level as given by the Boltzman factor Energy of a single oscillator

Treating Phonons like QM Oscillator Einstein Model = Heat capacity C can be found by differentiating the QM average phonon energy The energy of a harmonic oscillator and hence of a lattice mode of angular frequency at temperature T What happens to U as the temperature increases? The probability of the oscillator being in this level as given by the Boltzman factor Energy of a single oscillator

Treating Phonons like QM Oscillator Einstein Model = Heat capacity C can be found by differentiating the QM average phonon energy The energy of a harmonic oscillator and hence of a lattice mode of angular frequency at temperature T What happens to U as the temperature increases? Heat capacity is just d. U/d. T, need in terms of T. The probability of the oscillator being in this level as given by the Boltzman factor Energy of a single oscillator

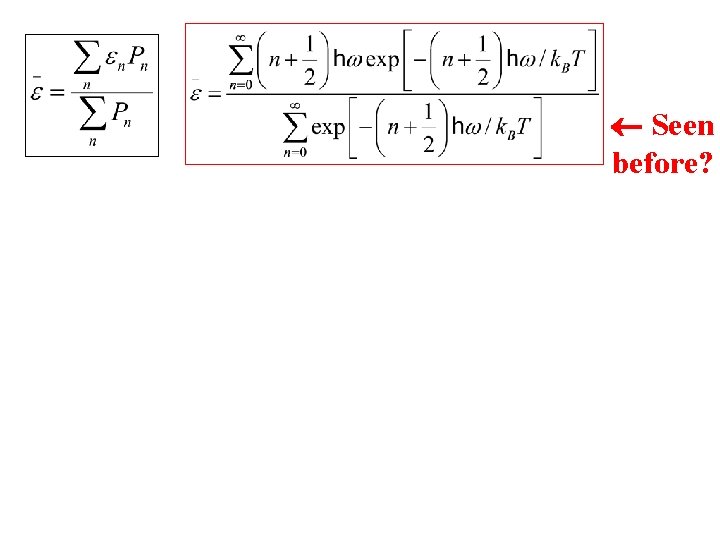
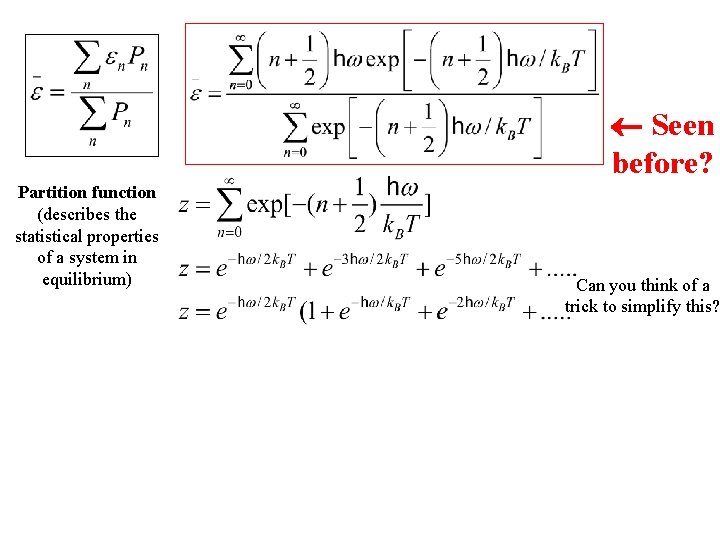
Seen before?

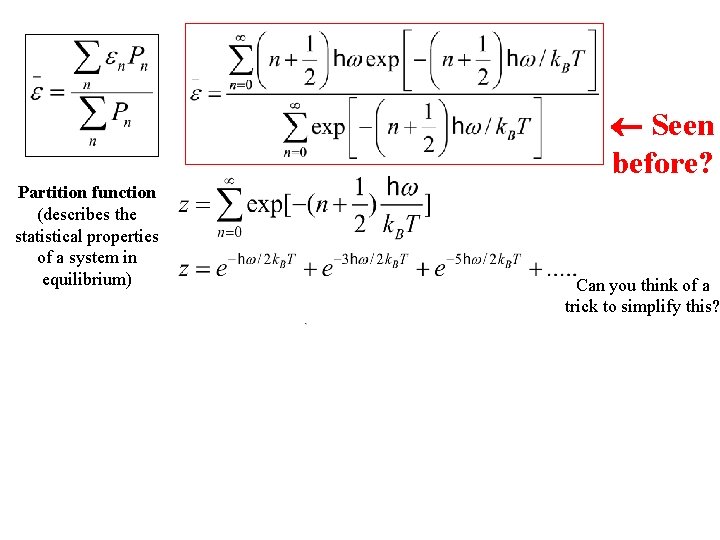
Seen before? Partition function (describes the statistical properties of a system in equilibrium) Can you think of a trick to simplify this?

Seen before? Partition function (describes the statistical properties of a system in equilibrium) Can you think of a trick to simplify this?

Seen before? Partition function (describes the statistical properties of a system in equilibrium) Can you think of a trick to simplify this? According to the Binomial expansion for x « 1 where

Seen before? Partition function (describes the statistical properties of a system in equilibrium) Can you think of a trick to simplify this? Will need soon According to the Binomial expansion for x « 1 where

Partition function (describes the statistical properties of a system in equilibrium) Seen before? ¬ What is dz/d. T? (on board) Can you think of a trick to simplify this? Will need soon According to the Binomial expansion for x « 1 where

Can be written as:

Can be written as:

Can be written as:

Can be written as:

Can be written as:

Can be written as:

Can be written as: Finally, the result is

This is the Mean Phonon Energy. The first term in the above equation is the zero-point energy. Even at 0 K atoms vibrate in the crystal.

This is the Mean Phonon Energy. The first term in the above equation is the zero-point energy. Even at 0 K atoms vibrate in the crystal. The number of phonons is given by the Bose-Einstein distribution as Planck distribution = (number of phonons) x (energy of phonon) = (second term in )

This is the Mean Phonon Energy. The first term in the above equation is the zero-point energy. Even at 0 K atoms vibrate in the crystal. The number of phonons is given by the Bose-Einstein distribution as Planck distribution = (number of phonons) x (energy of phonon) = (second term in ) The second term in the mean energy is the phonon contribution to thermal energy (since constant goes away with derivative).

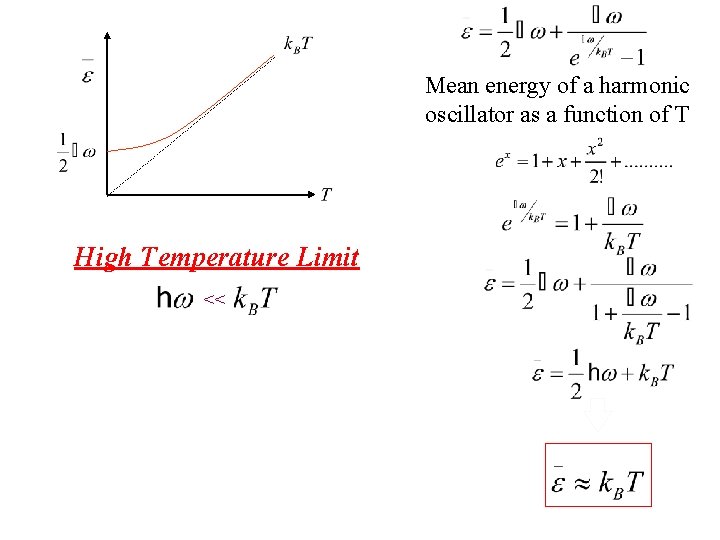
Mean energy of a harmonic oscillator as a function of T Low Temperature Limit What happens to exponential term?

Mean energy of a harmonic oscillator as a function of T Low Temperature Limit What happens to exponential term? Since exponential term gets bigger Zero Point Energy

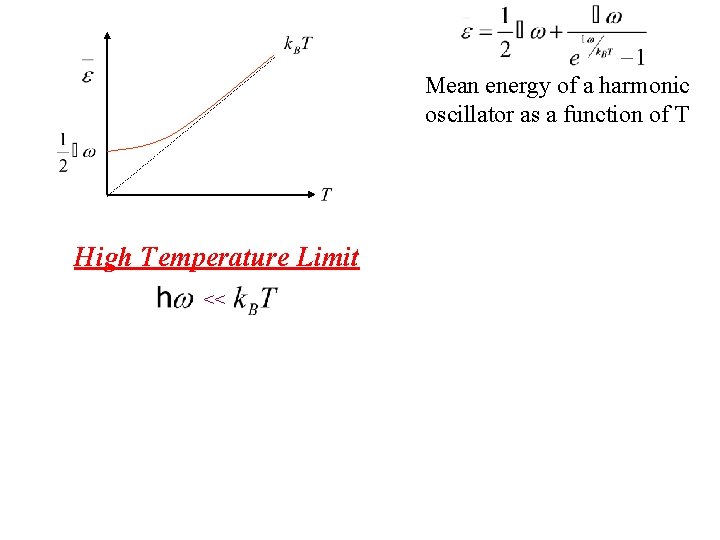
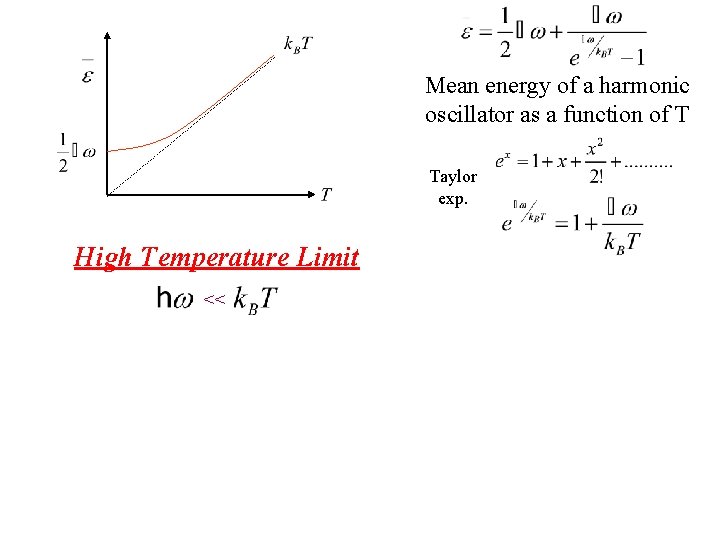
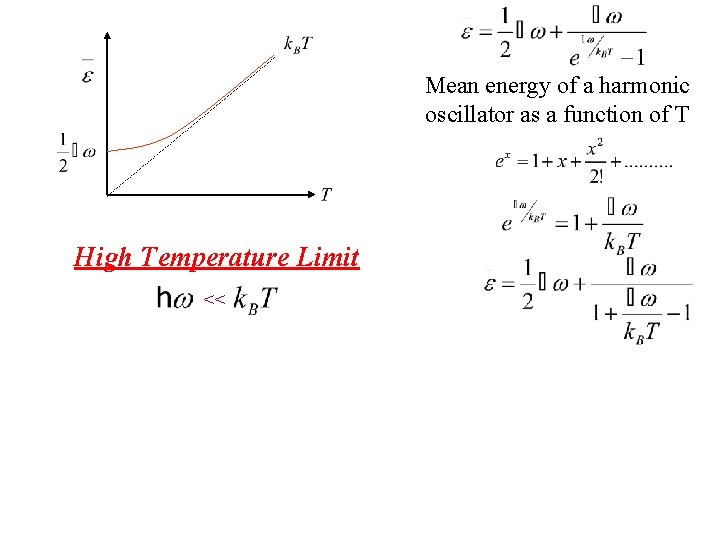
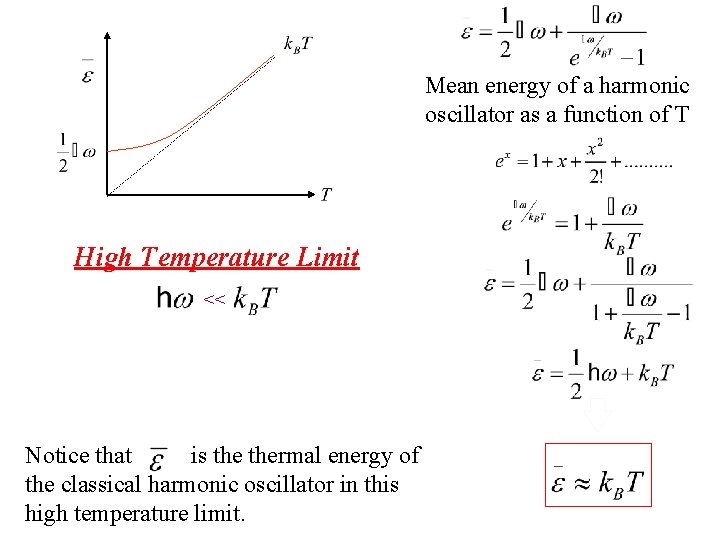
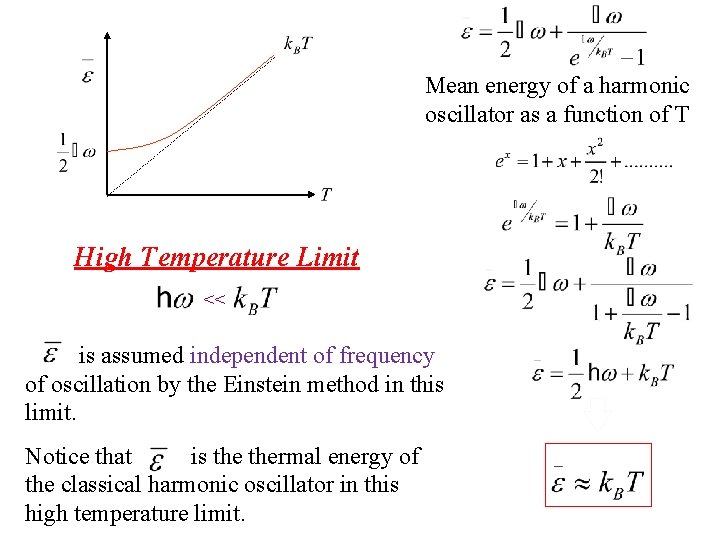
Mean energy of a harmonic oscillator as a function of T High Temperature Limit <<

Mean energy of a harmonic oscillator as a function of T Taylor exp. High Temperature Limit <<

Mean energy of a harmonic oscillator as a function of T High Temperature Limit <<

Mean energy of a harmonic oscillator as a function of T High Temperature Limit <<

Mean energy of a harmonic oscillator as a function of T High Temperature Limit << Notice that is thermal energy of the classical harmonic oscillator in this high temperature limit.

Mean energy of a harmonic oscillator as a function of T High Temperature Limit << is assumed independent of frequency of oscillation by the Einstein method in this limit. Notice that is thermal energy of the classical harmonic oscillator in this high temperature limit.

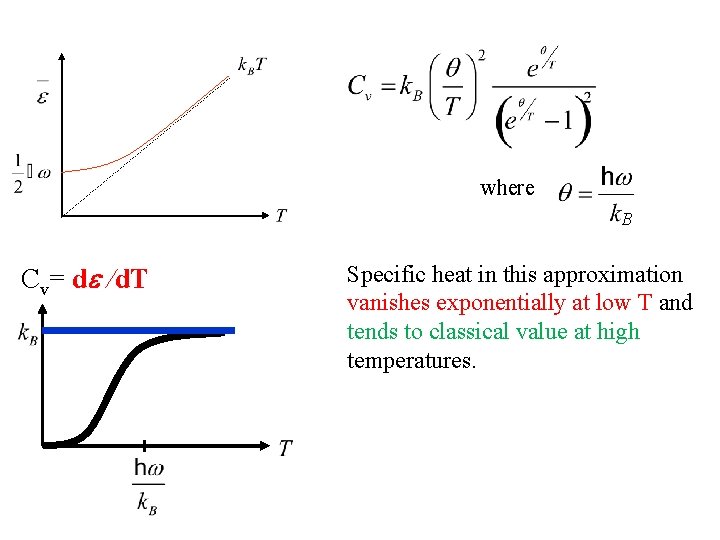
Heat Capacity C (Einstein Model) • Heat capacity C can be found by differentiating the average phonon energy

Heat Capacity C (Einstein Model) • Heat capacity C can be found by differentiating the average phonon energy

Heat Capacity C (Einstein Model) • Heat capacity C can be found by differentiating the average phonon energy Let B

Heat Capacity C (Einstein Model) • Heat capacity C can be found by differentiating the average phonon energy Let B

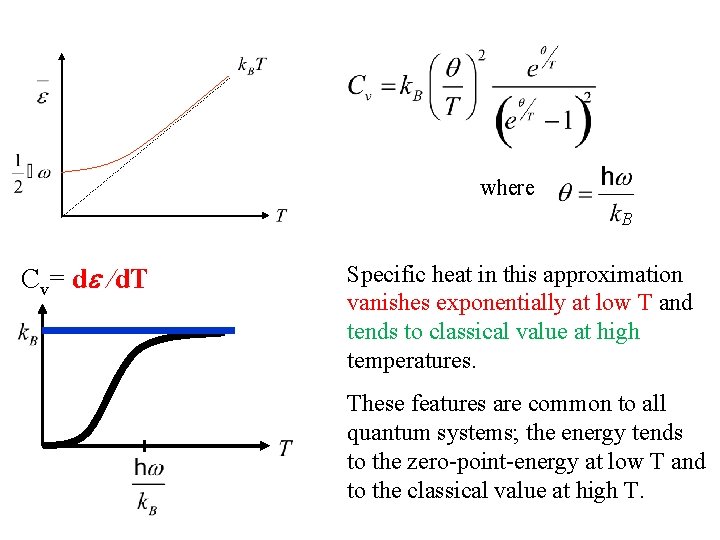
where B Cv= d /d. T Specific heat in this approximation vanishes exponentially at low T and tends to classical value at high temperatures.

where B Cv= d /d. T Specific heat in this approximation vanishes exponentially at low T and tends to classical value at high temperatures. These features are common to all quantum systems; the energy tends to the zero-point-energy at low T and to the classical value at high T.

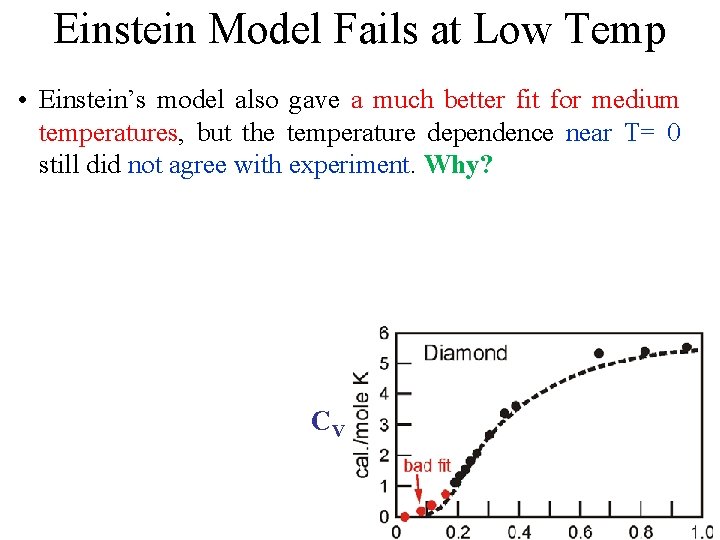
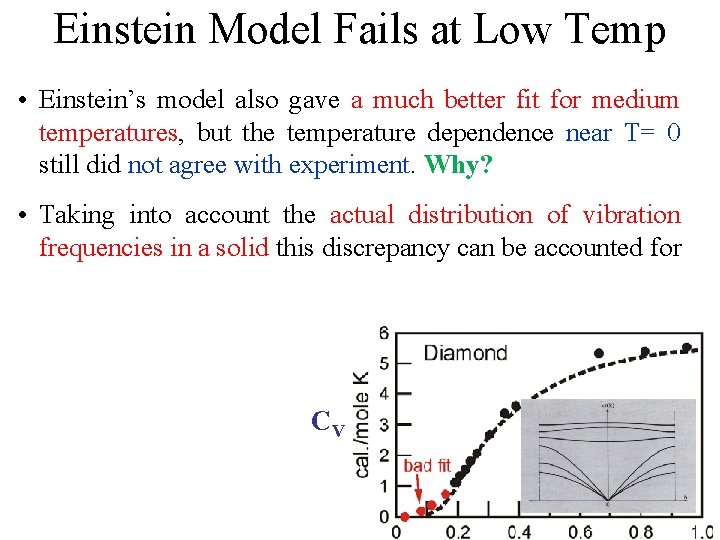
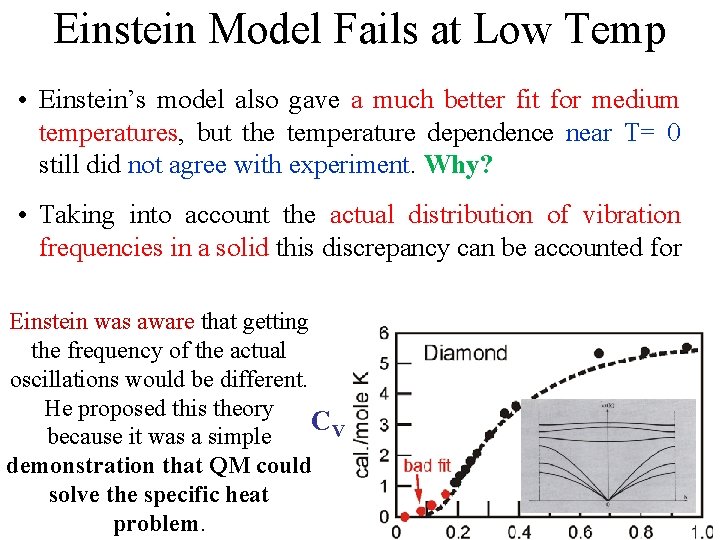
Einstein Model Fails at Low Temp • Einstein’s model also gave a much better fit for medium temperatures, but the temperature dependence near T= 0 still did not agree with experiment. Why? CV

Einstein Model Fails at Low Temp • Einstein’s model also gave a much better fit for medium temperatures, but the temperature dependence near T= 0 still did not agree with experiment. Why? • Taking into account the actual distribution of vibration frequencies in a solid this discrepancy can be accounted for CV

Einstein Model Fails at Low Temp • Einstein’s model also gave a much better fit for medium temperatures, but the temperature dependence near T= 0 still did not agree with experiment. Why? • Taking into account the actual distribution of vibration frequencies in a solid this discrepancy can be accounted for Einstein was aware that getting the frequency of the actual oscillations would be different. He proposed this theory CV because it was a simple demonstration that QM could solve the specific heat problem.

Incorporating the phonon distribution • Specific heat is still the temperature derivative of energy Cv= d. U /d. T

Incorporating the phonon distribution • Specific heat is still the temperature derivative of energy Cv= d. U /d. T • But now need to include the density of states D(E) (related to number of states N(E)) is not a constant Plus for fermions, minus for bosons Planck distribution

Density of Levels/States (confusing at first, read p. 108 -112) It’s ok if this doesn’t make sense by the end of today. It normally takes some practice before it becomes clear. That’s what homework and tests are for.

Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be occupied

Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be Imagine a multi-level parking lot. occupied The available number of spots in a particular floor of the parking spot is the density of states for that floor. It doesn't matter if it's occupied or not, just the number available matters for the DOS. The probability of finding a car in that particular floor is the product of the number of spots available and the fermi probability of occupation. Thus, each floor (energy level) will have its own DOS and probability. Karan Mehta, Ph. D student at Georgia Tech

Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be Imagine a multi-level parking lot. occupied The available number of spots in a particular floor of the parking spot is the density of states for that floor. It doesn't matter if it's occupied or not, just the number available matters for the DOS. The probability of finding a car in that particular floor is the product of the number of spots available and the fermi probability of occupation. Thus, each floor (energy level) will have its own DOS and probability. Karan Mehta, Ph. D student at Georgia Tech

Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be Imagine a multi-level parking lot. occupied ky kx The available number of spots in a particular floor of the parking spot is the density of states for that floor. It doesn't matter if it's occupied or not, just the number available matters for the DOS. The probability of finding a car in that particular floor is the product of the number of spots available and the fermi probability of occupation. Thus, each floor (energy level) will have its own DOS and probability. Karan Mehta, Ph. D student at Georgia Tech

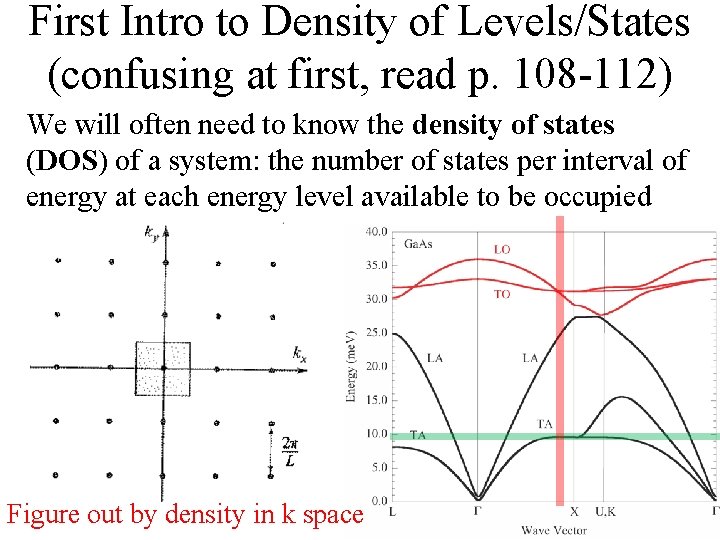
First Intro to Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be occupied

First Intro to Density of Levels/States (confusing at first, read p. 108 -112) We will often need to know the density of states (DOS) of a system: the number of states per interval of energy at each energy level available to be occupied Figure out by density in k space

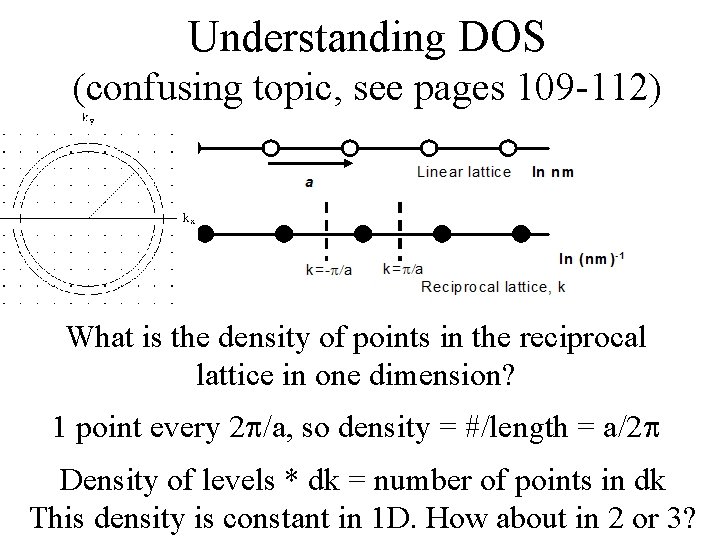
Understanding DOS (confusing topic, see pages 109 -112) What is the density of points in the reciprocal lattice in one dimension?

Understanding DOS (confusing topic, see pages 109 -112) What is the density of points in the reciprocal lattice in one dimension? 1 point every 2 /a, so density = #/length = a/2

Understanding DOS (confusing topic, see pages 109 -112) What is the density of points in the reciprocal lattice in one dimension? 1 point every 2 /a, so density = #/length = a/2 Density of levels * dk = number of points in dk This density is constant in 1 D. How about in 2 or 3?

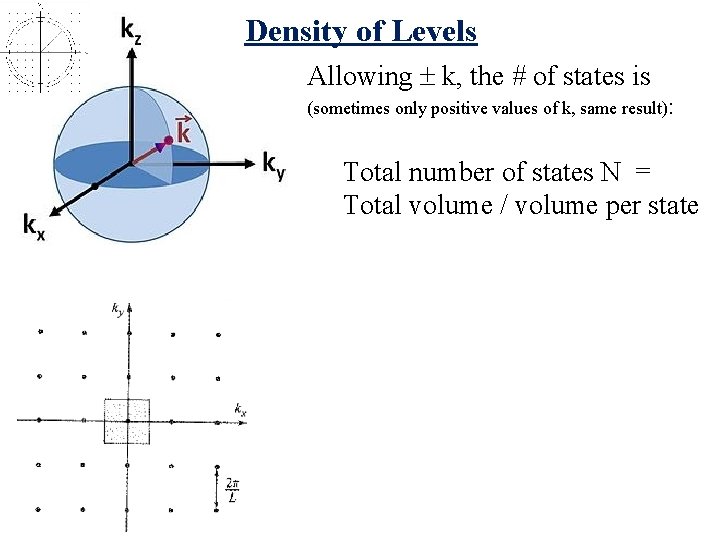
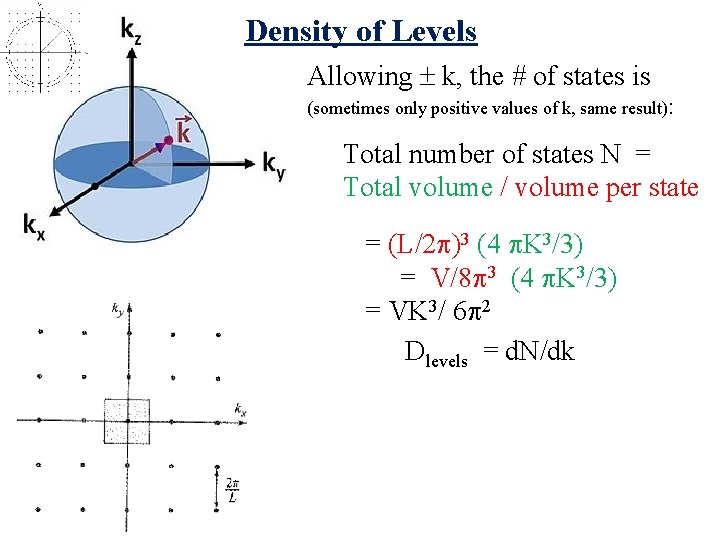
Density of Levels Allowing k, the # of states is (sometimes only positive values of k, same result): Total number of states N = Total volume / volume per state

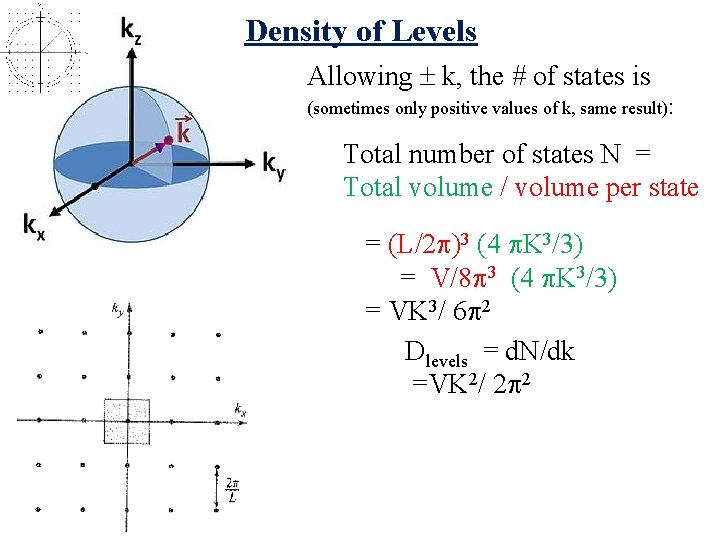
Density of Levels Allowing k, the # of states is (sometimes only positive values of k, same result): Total number of states N = Total volume / volume per state = (L/2 )3 (4 K 3/3) = V/8 3 (4 K 3/3) = VK 3/ 6 2 Dlevels = d. N/dk

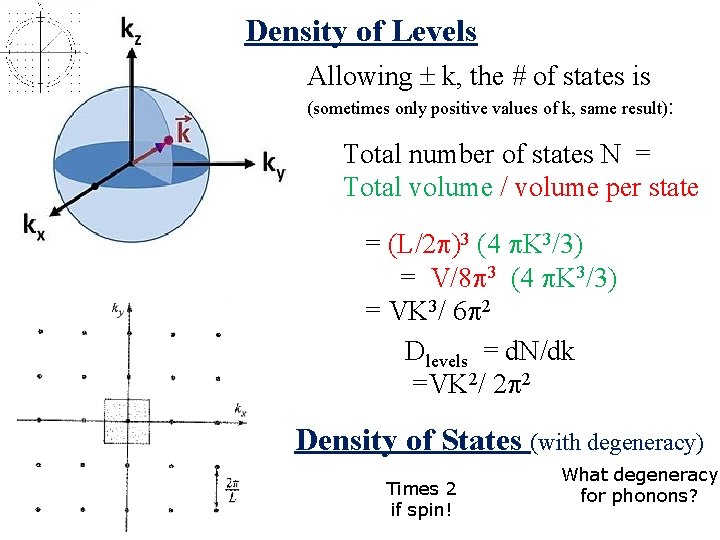
Density of Levels Allowing k, the # of states is (sometimes only positive values of k, same result): Total number of states N = Total volume / volume per state = (L/2 )3 (4 K 3/3) = V/8 3 (4 K 3/3) = VK 3/ 6 2 Dlevels = d. N/dk =VK 2/ 2 2

Density of Levels Allowing k, the # of states is (sometimes only positive values of k, same result): Total number of states N = Total volume / volume per state = (L/2 )3 (4 K 3/3) = V/8 3 (4 K 3/3) = VK 3/ 6 2 Dlevels = d. N/dk =VK 2/ 2 2 Density of States (with degeneracy) Times 2 if spin! What degeneracy for phonons?

Finding the 3 d density of states D(E) for Photons Good analogy for low temp phonons. Why?

Finding the 3 d density of states D(E) for Photons Good analogy for low temp phonons. Why?

Finding the 3 d density of states D(E) for Photons Good analogy for low temp phonons. Why?

Finding the 3 d density of states D(E) for Photons (Same for spin since 2 polarization states) Good analogy for low temp phonons. Why?

Finding the 3 d density of states D(E) for Photons (Same for spin since 2 polarization states) V Good analogy for low temp phonons. Why?

Finding the 3 d density of states D(E) for Photons (Same for spin since 2 polarization states) V Good analogy for low temp phonons. Why?

Density of States (for Photons)

Density of States (for Photons)

Density of States (for Photons)
 Insidan region jh
Insidan region jh How can a machine make work easier for you
How can a machine make work easier for you Sometimes you win some sometimes you lose some
Sometimes you win some sometimes you lose some They say it only takes a little faith to move a mountain
They say it only takes a little faith to move a mountain If you think you can you can poem
If you think you can you can poem Through you i can do anything i can do all things
Through you i can do anything i can do all things I can easier teach twenty
I can easier teach twenty If you can imagine it you can achieve it
If you can imagine it you can achieve it If you can't measure it you can't manage it
If you can't measure it you can't manage it If you can't measure it you can't control it
If you can't measure it you can't control it If you cannot measure it you cannot manage it
If you cannot measure it you cannot manage it Kurzfristiges fremdkapital
Kurzfristiges fremdkapital Can you please tell me some information that
Can you please tell me some information that 3 things you can cut answer
3 things you can cut answer Things you can climb
Things you can climb Can you heat me
Can you heat me Pulley ama formula
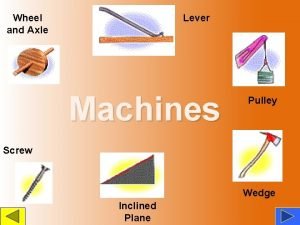
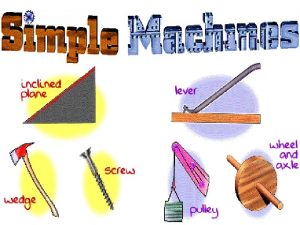
Pulley ama formula Device that makes doing work easier
Device that makes doing work easier Types of pulley
Types of pulley Uses of pully
Uses of pully Gas from becomes easier to compress
Gas from becomes easier to compress How does a wedge make work easier
How does a wedge make work easier Brain wrinkles southwest asia
Brain wrinkles southwest asia Effort arm and resistance arm
Effort arm and resistance arm An easier way to choose contrasting structures is to pick
An easier way to choose contrasting structures is to pick Why its easier than ever
Why its easier than ever Is caesar cipher monoalphabetic
Is caesar cipher monoalphabetic Push
Push Remaining
Remaining Effforce
Effforce Seesaw
Seesaw Credit unions are for-profit organizations. true false
Credit unions are for-profit organizations. true false Why was italy easier to unify than greece
Why was italy easier to unify than greece Why are footprints easier to cast than tire tracks
Why are footprints easier to cast than tire tracks Communication-it's much easier than done
Communication-it's much easier than done The roman world takes shape
The roman world takes shape Is ice cream countable noun
Is ice cream countable noun Contact and noncontact forces
Contact and noncontact forces Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some say the world will end in fire some say in ice
Some say the world will end in fire some say in ice Some trust in horses
Some trust in horses Kinds of comparison
Kinds of comparison You can tell harris about it just ____(easily) as i can
You can tell harris about it just ____(easily) as i can Positive degree examples
Positive degree examples What is the point of uchendu’s lecture to okonkwo?
What is the point of uchendu’s lecture to okonkwo? Name some things
Name some things Some things never change
Some things never change Some things are caught not taught
Some things are caught not taught Are some things unknowable?
Are some things unknowable? What did mr underwood's editorial say
What did mr underwood's editorial say Blue things
Blue things Sensitivity in life processes
Sensitivity in life processes Specific heat of water
Specific heat of water Latent heat and specific latent heat
Latent heat and specific latent heat Example of dry heat
Example of dry heat You can't turn right here. you turn left
You can't turn right here. you turn left Have a daughter so you can argue
Have a daughter so you can argue Jared peet
Jared peet Standardasation
Standardasation So you think you can argue
So you think you can argue Turn right turn left go straight ahead
Turn right turn left go straight ahead You can be just the one you wanna be
You can be just the one you wanna be I can hear you quite well. you not shout
I can hear you quite well. you not shout So you think you can argue
So you think you can argue Check if you can remember what tim tells you
Check if you can remember what tim tells you Silk is a natural protein fiber some forms of which can be
Silk is a natural protein fiber some forms of which can be Which natural polymer comes from a cocoon? rubber wool silk
Which natural polymer comes from a cocoon? rubber wool silk Explain how some hail can become baseball sized
Explain how some hail can become baseball sized What do you do to protect the environment
What do you do to protect the environment Materials that completely block light
Materials that completely block light Because of libraries we can say these things
Because of libraries we can say these things More things can be dissolved in sulfuric acid than in water
More things can be dissolved in sulfuric acid than in water What three actions consume traction
What three actions consume traction How can i memorize things quickly
How can i memorize things quickly What we learn from ants
What we learn from ants Bird riddles
Bird riddles It is something concrete that stands for something abstract
It is something concrete that stands for something abstract Bottle banks milton keynes
Bottle banks milton keynes We can do no great things only small
We can do no great things only small Philippians 4 6 esv
Philippians 4 6 esv Is invisible force than can produce heat, light and motion
Is invisible force than can produce heat, light and motion