Sistemas Dinmicos com Campo de Direes Parcialmente Conhecido

Sistemas Dinâmicos com Campo de Direções Parcialmente Conhecido Laécio Carvalho de Barros (laeciocb@ime. unicamp. br) IMECC - Unicamp

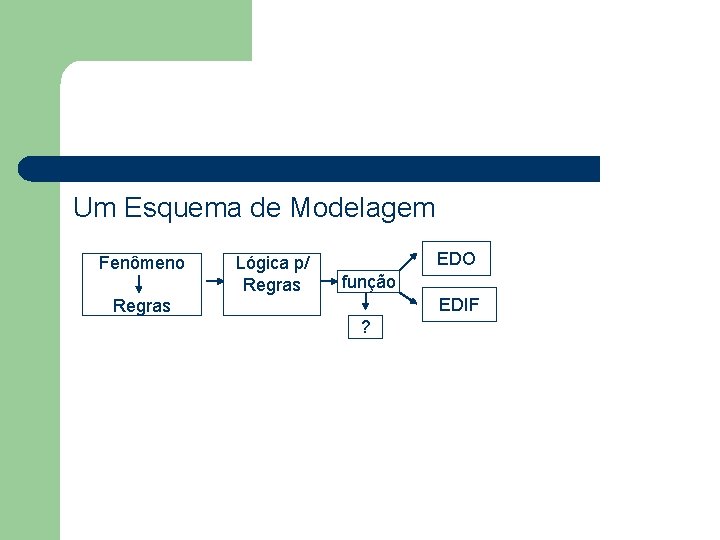
Um Esquema de Modelagem Fenômeno Lógica p/ Regras EDO função EDIF Regras ?

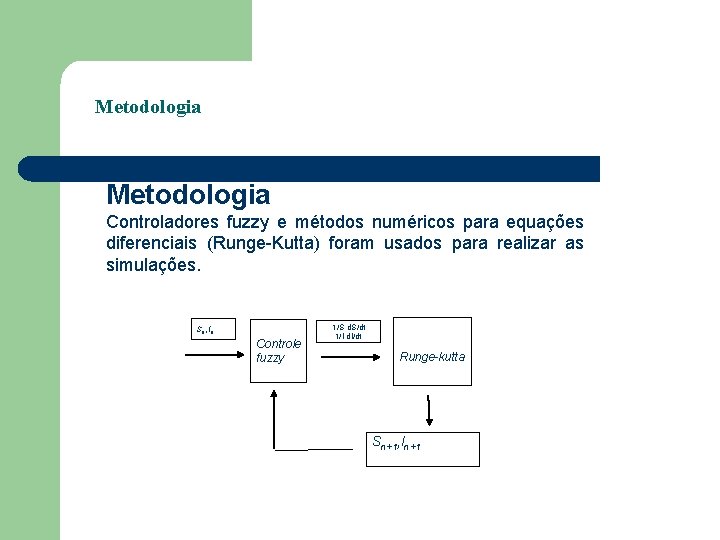
Metodologia Controladores fuzzy e métodos numéricos para equações diferenciais (Runge-Kutta) foram usados para realizar as simulações. Sn, In Controle fuzzy 1/S d. S/dt 1/I d. I/dt Runge-kutta Sn+1, In+1

Princípio bem aceito Ecologia “Uma população varia a uma taxa proporcional a própria população em cada instante t. ”

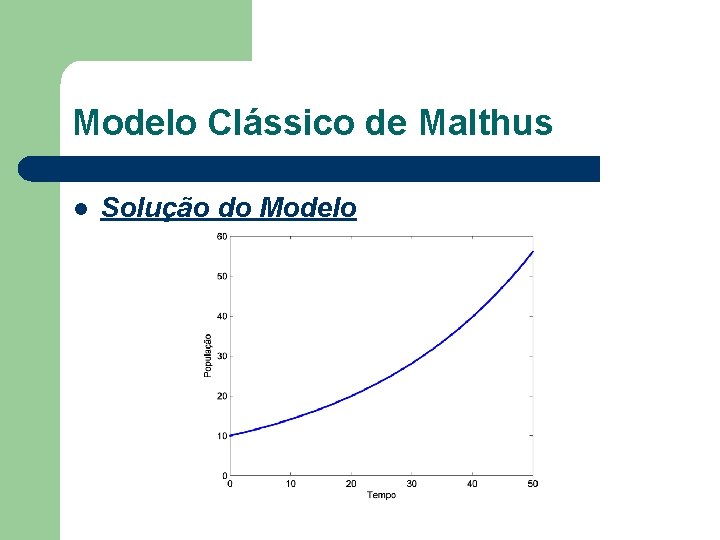
Modelo Clássico de Malthus Característica do Modelo: A variação é dada pela derivada. Nesse caso tem-se o seguinte PVI: l Obs. : crescimento específico (dx/dt) constante.

Modelo Clássico de Malthus l Solução do Modelo

Lógica Fuzzy: o começo Lofti Zadeh publica (1965) o artigo com as primeiras Idéias sobre conjuntos fuzzy. Principal interesse era armazenar conceitos como “aproximadamente”, “em torno de” etc.

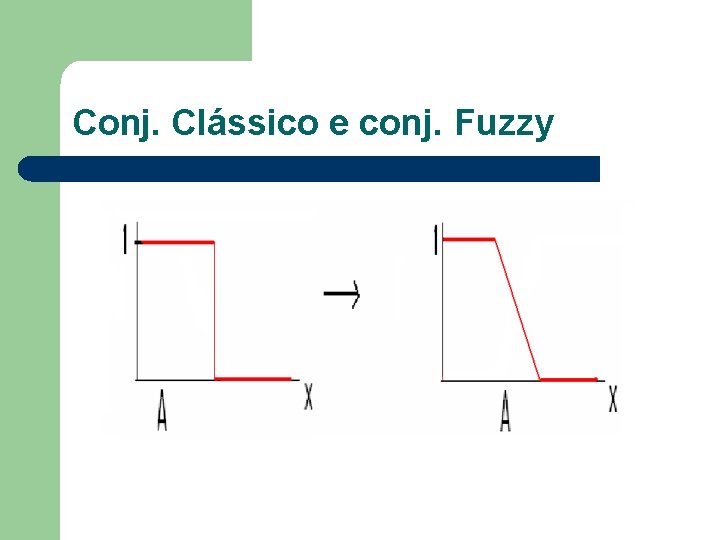
Conj. Clássico e conj. Fuzzy

Função de pertinência Um subconjunto fuzzy F de U é definido por uma função µ : U [0, 1], chamada função de pertinência de F. µ (x) indica o grau com que “x” é um elemento de F. Ex. : “em torno de 100” µ(x) =

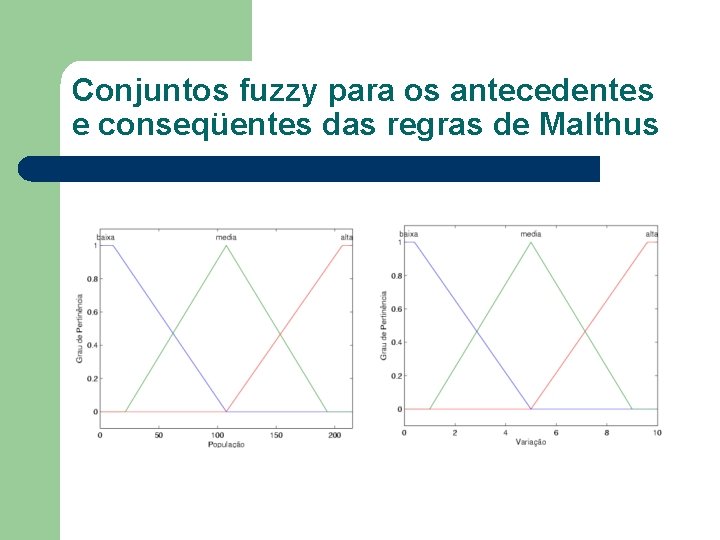
Malthus com regras l Uma primeira tentativa de modelagem para tal princípio poderia nos levar às seguintes regras -Se a população(X) é baixa(B) então a variação é baixa(B); -Se a população(X) é média(M) então a variação é média(M); -Se a população(X) é alta(A) então a variação é alta(A).

Conjuntos fuzzy para os antecedentes e conseqüentes das regras de Malthus

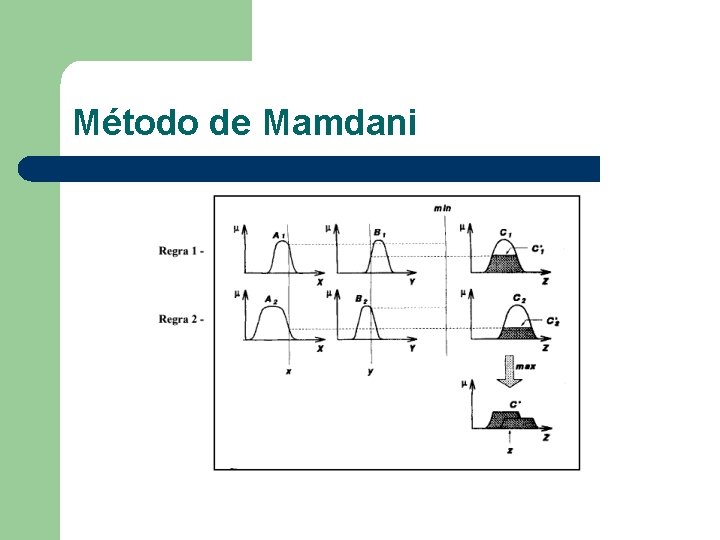
Método de Mamdani

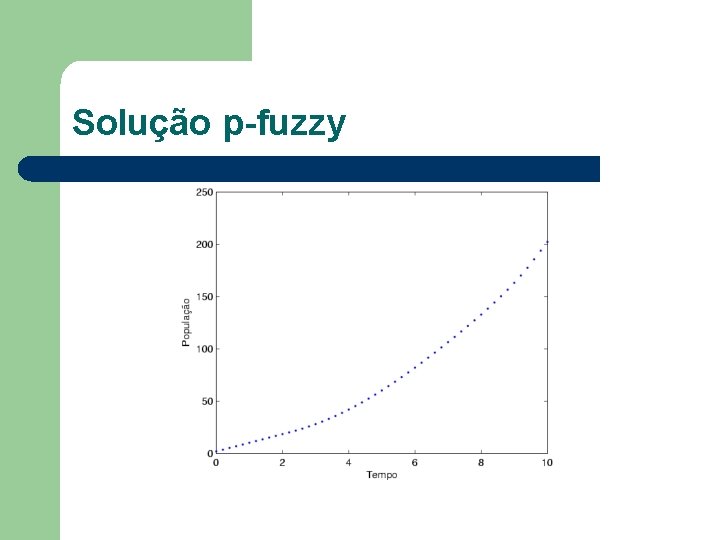
Solução p-fuzzy

Modelo presa-predador de Lotka. Volterra O modelo presa-predador clássico de Lotka-Volterra, que se tornou um paradigma da Biomatemática, pressupõe que: l 1 - Tanto as presas como os predadores estão distribuídos uniformemente num mesmo habitat, ou seja, todos os predadores têm a mesma chance de encontrar cada presa; l 2 - O encontro entre os indivíduos das duas espécies seja ao acaso, a uma taxa proporcional ao tamanho das duas populações; l 3 - A população de presas x(t) cresce exponencialmente na ausência de predadores (crescimento ilimitado por escassez de predadores); l 4 - A população de predadores y(t) decresce exponencialmente na ausência de presas (decrescimento por escassez de alimento); l 5 - A população de predadores é favorecida pela abundância de presas; l 6 - A população de presas é desfavorecida pelo aumento de predadores.

Modelo Clássico do tipo Presa-Predador de Lotka-Volterra l Estas seis hipóteses são resumidas nas equações abaixo, denominadas Modelo de Lotka-Volterra:

Interpretação para parâmetros l a: taxa de crescimento da população de presas na ausência de predadores; l (α/β): a eficiência de predação, isto é, a eficiência de conversão de uma unidade de massa de presas em uma unidade de massa de predadores, já que α representa a proporção de sucesso dos ataques dos predadores e β a taxa de conversão de biomassa das presas em predadores; l b : taxa de mortalidade de predadores na ausência de presas; Obs. : Os pontos críticos do sistema são: (0, 0), um ponto de sela instável, e ((b/β), (a/α)) que é um centro estável.

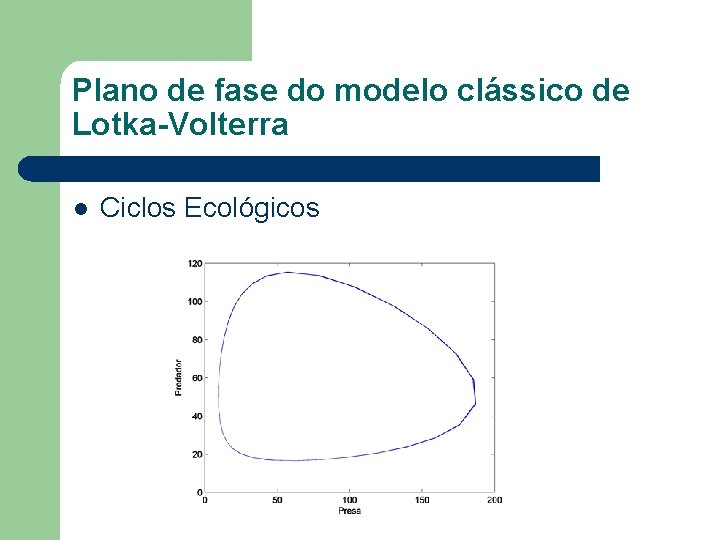
Plano de fase do modelo clássico de Lotka-Volterra l Ciclos Ecológicos

Re-interpretando as seis hipóteses comentadas acima: A hipótese "1" significa apenas que, dentro de cada espécie, o ambiente não privilegia nenhum indivíduo. Portanto é natural que as variáveis de estado sejam apenas quantidades; "2" significa apenas que há interação entre as espécies; "3" indica que não há auto-inibição nas presas, isto é, para um dado número de predadores, o crescimento específico das presas é constante, podendo ser positivo ou negativo; "4" como em "3", espera-se que, para um dado número de presas, o crescimento específico dos predadores seja constante, podendo ser positivo ou negativo; "5" apenas indica que o crescimento específico dos predadores aumenta com o número de presas; "6" significa que o crescimento específico das presas diminui com o aumento dos predadores. Resumidamente, as hipótese de 3 a 6 indicam que, dada uma certa quantidade de uma espécie, a outra tem crescimento (decrescimento) malthusiano.

Arquitetura para modelo p-fuzzy de Lotka-Volterra

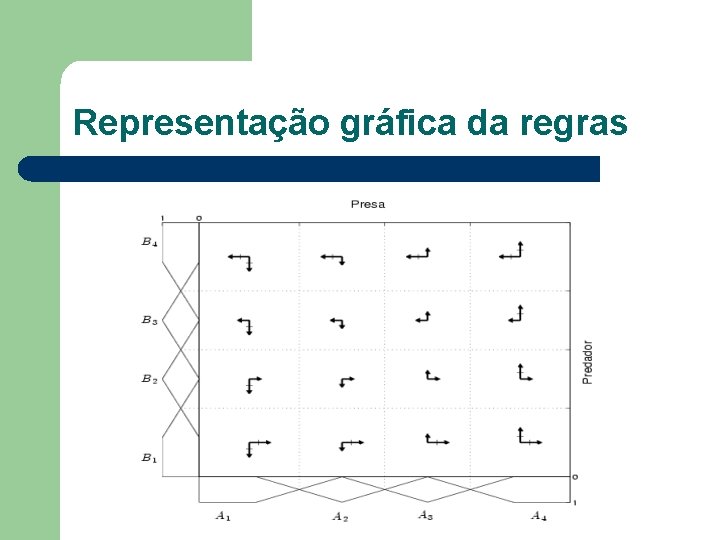
Representação gráfica da regras

Base de Regras para Lotka-Volterra l l l l Se X é A 1 e Y é B 1 então (1/X)((d. X)/(dt)) é P 2 e (1/Y)((d. Y)/(dt)) é N 2 Se X é A 2 e Y é B 1 então (1/X)((d. X)/(dt)) é P 2 e (1/Y)((d. Y)/(dt)) é N 1 Se X é A 3 e Y é B 1 então (1/X)((d. X)/(dt)) é P 2 e (1/Y)((d. Y)/(dt)) é P 1 Se X é A 4 e Y é B 1 então (1/X)((d. X)/(dt)) é P 2 e (1/Y)((d. Y)/(dt)) é P 2 Se X é A 1 e Y é B 2 então (1/X)((d. X)/(dt)) é P 1 e (1/Y)((d. Y)/(dt)) é N 2 Se X é A 2 e Y é B 2 então (1/X)((d. X)/(dt)) é P 1 e (1/Y)((d. Y)/(dt)) é N 1 Se X é A 3 e Y é B 2 então (1/X)((d. X)/(dt)) é P 1 e (1/Y)((d. Y)/(dt)) é P 1 Se X é A 4 e Y é B 2 então (1/X)((d. X)/(dt)) é P 1 e (1/Y)((d. Y)/(dt)) é P 2 Se X é A 1 e Y é B 3 então (1/X)((d. X)/(dt)) é N 1 e (1/Y)((d. Y)/(dt)) é N 2 Se X é A 2 e Y é B 3 então (1/X)((d. X)/(dt)) é N 1 e (1/Y)((d. Y)/(dt)) é N 1 Se X é A 3 e Y é B 3 então (1/X)((d. X)/(dt)) é N 1 e (1/Y)((d. Y)/(dt)) é P 1 Se X é A 4 e Y é B 3 então (1/X)((d. X)/(dt)) é N 1 e (1/Y)((d. Y)/(dt)) é P 2 Se X é A 1 e Y é B 4 então (1/X)((d. X)/(dt)) é N 2 e (1/Y)((d. Y)/(dt)) é N 2 Se X é A 2 e Y é B 4 então (1/X)((d. X)/(dt)) é N 2 e (1/Y)((d. Y)/(dt)) é N 1 Se X é A 3 e Y é B 4 então (1/X)((d. X)/(dt)) é N 2 e (1/Y)((d. Y)/(dt)) é P 1 Se X é A 4 e Y é B 4 então (1/X)((d. X)/(dt)) é N 2 e (1/Y)((d. Y)/(dt)) é P 2

Soluções para o p-fuzzy Lotka-Volterra l Em cada instante t, o número de presas e de predadores é dado pelas fórmulas

Estimativas onde e são as saídas do controlador l Assim, os valores de x(t) e y(t)e são. estimados correspondentes às entradas fórmulas pelas

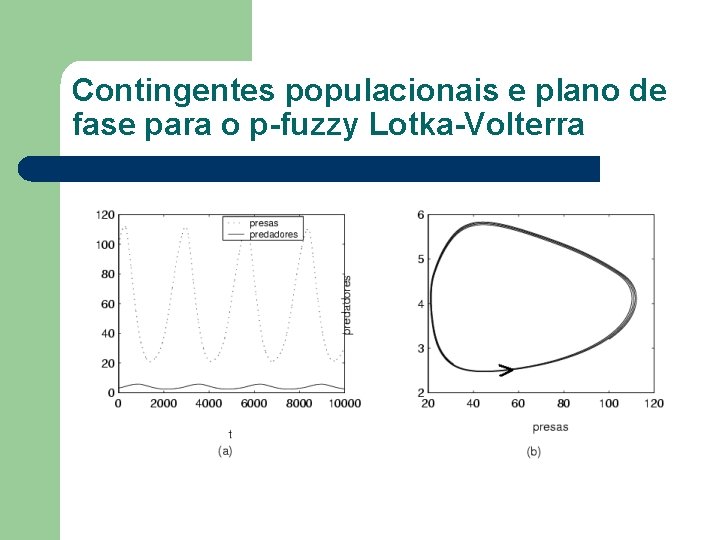
Contingentes populacionais e plano de fase para o p-fuzzy Lotka-Volterra