Sesin Tcnica 5 Diseos de Muestreo PRIMERA PARTE

Sesión Técnica 5 Diseños de Muestreo PRIMERA PARTE

Diseño de muestreo y diseño de la encuesta Diseño de muestreo de una encuesta: conjunto de técnicas para seleccionar una muestra probabilística y los métodos de estimación empleados para inferir los valores de los parámetros de interés a partir de la muestra. Diseño de la encuesta: definiciones, métodos y procedimientos concernientes a todas las fases necesarias para conducir la operación.

Conceptos previos Poblaciones: Una población (U) es un conjunto de (N) elementos. Un elemento se denotará por i. Variables: Cada elemento tiene asociados valores de variables de interés. Sea yi el valor de la variable y en el i-ésimo elemento. Parámetros: Son valores desconocidos de la población que nos interesa estimar. Muestra: Una parte (de tamaño n) de la población. Una muestra se denotará por M.

Conceptos previos (cont. ) • Conjunto de observaciones: A cada elemento seleccionado en la muestra la “observamos” y tendremos al conjunto de observaciones: O : {yi: i Є M}. • Estimador: Función (T) de las observaciones (T=t(O)), que usamos para estimar los parámetros. • Error de muestreo: Error proveniente de observar M y no U. (“Error intrínseco”) • Errores no de muestreo: Los otros errores.

Conceptos previos (cont. ) ¿Cómo se mide el error de muestreo? Como veremos más adelante la varianza estimada del estimador juega un papel clave porque ella es una medida de la variabilidad entre las estimaciones que esperaríamos si se tomaran muchas muestras. El problema es que la varianza depende de la unidad de medida, por ello es conveniente utilizar el Coeficiente de Variación que es libre de unidad de medida: o usar intervalos de confianza

Diseños de muestreo más comunes • Muestreo Aleatorio Simple (MAS) • Muestreo Aleatorio Estratificado (MAE) • Muestreo por conglomerados: – Con selección MAS – Con selección proporcional al tamaño (PPT) u otro diseño de probabilidad variable. • Muestreo sistemático • Muestreo en varias etapas

MUESTREO ALEATORIO SIMPLE

Muestreo Aleatorio Simple (1) • Definición: M. A. S. es el diseño en el cual cada muestra posible tiene igual probabilidad de selección ( ). • Una consecuencia es que en MAS cada elemento de la población tiene la misma probabilidad de ser seleccionado en la muestra (n/N ). • Estos procedimientos de muestreo se conocen como Métodos de selección equiprobables (EPSEM). • MAS es EPSEM pero no todos los EPSEM son MAS.

Muestreo Aleatorio Simple (2) ¿Cómo se selecciona una MAS? Por definición, cada elemento (i) de los N de la población tiene igual probabilidad de ser seleccionado (pi = n/N). Una forma práctica es elegir n de a uno y sin reponer sorteando n números aleatorios distintos entre 1 y N. Usando una “tabla de números aleatorios” o un programa de cómputo (por ejemplo la función “ALEATORIO” de Excel® ).

Muestreo Aleatorio Simple (3) Estimadores insesgados: - Para la media poblacional (μ), la media muestral: - Para el total poblacional (Nμ): - Para la varianza poblacional la varianza muestral corregida: siendo

Muestreo Aleatorio Simple (4) • Intervalos de confianza: Un intervalo de confianza (IC) al (1 -α)% es un intervalo que contiene al verdadero valor del parámetro poblacional con probabilidad igual a 1 -α. • IC para la media (n>50): siendo el valor de la distribución Normal Estándar que acumula 1 -α/2 de probabilidad: α = 0. 1 α = 0. 05 z 1 -α = 1. 645 z 1 -α = 1. 96 α = 0. 01 z 1 -α = 2. 576

Muestreo Aleatorio Simple (5) Determinación del tamaño de la muestra: Sea e el error máximo permitido (en la unidad original), entonces el n que garantiza ese error máximo para la estimación de μ al nivel de confianza 1 -α en el MAS es: Problema: ¿σ?

Muestreo Aleatorio Simple (6) • Caso particular: Estimación de proporciones (o porcentajes). Si el objetivo es estimar una proporción, las cosas se simplifican porque la proporción no es más que la media de una variable “y” que sólo toma los valores 0 ó 1. Los estimadores insesgados son: -Para la proporción poblacional: la proporción observada en la muestra -La estimación de la varianza se simplifica porque en este caso s 2=(n/n-1)(p(1 -p)) -Para los intervalos de confianza hay que tener cuidado con la aproximación Normal (ver tabla en las Notas) -En la determinación del n, σ2 puede acotarse por 0. 25

Muestreo Aleatorio Simple (7) Estimación de una razón (o cociente): Dos casos: a) La razón es el parámetro a estimar b) La razón la estimamos para estimar otro parámetro. Caso a): Se quiere estimar el cociente y/x (por ejemplo: rendimiento=producción/área) y se estima la media de “y” y la media de “x” y se usa como estimador a: Caso b): Se tiene información auxiliar sobre “x” sea “X”, se usa esa información para estimar el total (o la media de Y) mediante: Con MAS, es un estimador sesgado de la verdadera razón

MUESTREO ALEATORIO ESTRATIFICADO

Muestreo Aleatorio Estratificado (1) • Definición: La población de N elementos se divide en L grupos llamados estratos. Se toman luego M. A. S. dentro de cada estrato. • Consecuencia: la probabilidad de selección de un elemento de la población ya no es constante (depende del estrato al cual pertenece). • ¿Cuándo es más eficiente? Cuando los estratos son muy homogéneos internamente y heterogéneos entre ellos.

Muestreo Aleatorio Estratificado (2) Sean: Nh = tamaño de la población del estrato h. nh = tamaño de la muestra del estrato h. yhi = valor de y en la i-ésima unidad del estrato h μh = media poblacional en el estrato h Por tanto: ; ;

Muestreo Aleatorio Estratificado (3) Estimadores insesgados: - Para la media poblacional (μ): - Para el total poblacional (Nμ): - Para la varianza poblacional (σ2): donde sh 2 se define como antes, pero a nivel del estrato

Muestreo Aleatorio Estratificado (4) • Intervalos de confianza: Lo ya desarrollado para el M. A. S. vale aquí sustituyendo por (cuidado con la aproximación Normal) • Determinación del tamaño de muestra: Ahora debemos determinar tantos tamaños de muestra como estratos (L). Se determina el tamaño n de la muestra total y se distribuye entre los estratos, ¿cómo?

Muestreo Aleatorio Estratificado (5) • Asignaciones usuales: • Distribución proporcional: asignamos a cada estrato una proporción de n, igual a la proporción de N del estrato: nh = n(Nh /N) ; • Distribución óptima: además de Nh considera la dispersión de los valores de y en el estrato:

Muestreo Aleatorio Estratificado (6) • Determinación del n: 1) En el caso de “asignación proporcional”: 2) En el caso de la “asignación óptima”:

Muestreo Aleatorio Estratificado (7) • Problemas a resolver: 1) ¿Cómo aproximar los L valores σh ? 2) ¿L? 3) ¿Puntos de corte de los estratos? 4) ¿Qué variable de estratificación usar? 5) ¿Cómo controlar el error de estimación de varios parámetros a la vez? (este problema vale para todos los diseños)

Muchas gracias

Sesión Técnica 5 Diseños de Muestreo SEGUNDA PARTE

Post estratificación • Concepto: Se desea clasificar las unidades de una población en grupos a partir de la muestra y luego de haber realizado la encuesta, pero el diseño no fue estratificado. • Supongamos que extrajimos n unidades mediante M. A. S. y luego se desea post-estratificar la población en L estratos. La diferencia con el M. A. E. es que los nh pasan a ser variables aleatorias (cambian de muestra a muestra). Lo interesante ( e intuitivo) es que el valor esperado de esa variable aleatoria es: es decir “en promedio” la muestra de n unidades se va a distribuir como en la asignación proporcional.

Muestreo por conglomerados(1) • Definición: La población se divide en grupos (“conglomerados”) y cada grupo pasa a ser una unidad de muestreo. • Tipos: a) Si la unidad final de muestreo es el conglomerado: “Muestreo por conglomerados mono-etápico” b) Si los conglomerados seleccionados se sub-muestrean: “Muestreo por conglomerados poli-etápico” (en dos etapas, en tres etapas, etc. ). En este caso se tendrán: “Unidades primarias de muestreo (UPM ó PSU), unidades secundarias de muestreo (USM ó SSU), y así sucesivamente. • ¿Cuándo es más eficiente? Cuando los conglomerados son muy heterogéneos dentro y homogéneos entre sí

Muestreo por conglomerados(2) Razones para usar el Muestreo por conglomerados: 1. Construcción de marcos: listamos solo los elementos de los conglomerados seleccionados. 2. Economía de recursos: una vez en el conglomerado es más económico visitar los elementos del conglomerado que elementos dispersos.

Muestreo por conglomerados mono-etápico (1) • Concepto: La población se divide en N conglomerados y hay Mj unidades en el j-ésimo conglomerado. Llamando M al número de unidades originales de la población: Sea yjk el valor de la variable en la k-ésima unidad secundaria del j-ésimo conglomerado. Entonces, el total poblacional de Y es La media por unidad es: La media por conglomerado es:

Muestreo por conglomerados mono-etápico (2) • Caso 1: De los N conglomerados elegimos n mediante M. A. S y “barremos” todas las unidades de los conglomerados seleccionados. Los estimadores insesgados de la media y la varianza surgen facilmente del MAS ya que cada conglomerado es ahora unidad que tiene asociada el total del valor de la variable en el conglomerado (es decir la suma de los valores de y para los elementos del conglomerado). (Observación: en este caso no hay contribución a la varianza muestral de la varianza dentro del conglomerado porque se “censan” todos los elementos del conglomerado, es decir el total de cada conglomerado muestreado se obtiene “sin error de muestreo”

Muestreo por conglomerados mono-etápico (3) Si la variable y está altamente correlacionada con el tamaño del conglomerado, se demuestra que el estimador de razón: es muy eficiente. Es sesgado pero el sesgo disminuye rápidamente al aumentar n. (Ver estimador de la varianza en las notas § 2. 3. 2 (fórmula [35]))

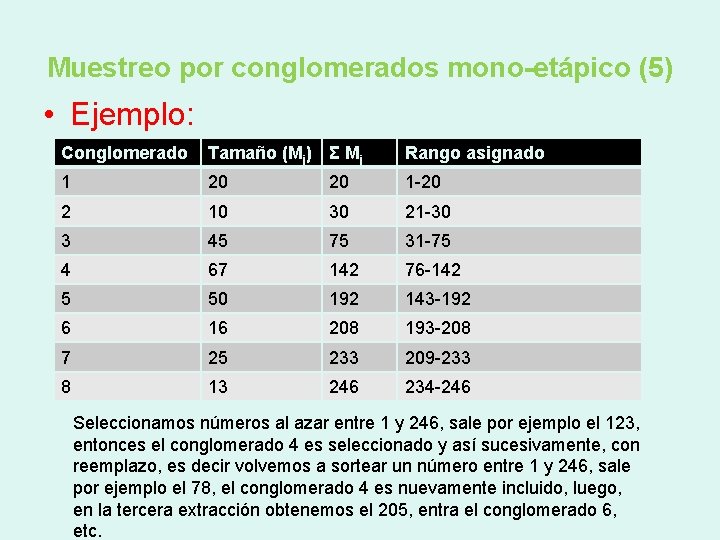
Muestreo por conglomerados mono-etápico (4) • Caso 2: De los N conglomerados elegimos n mediante muestreo con probabilidad proporcional al tamaño (ppt) (con repetición) y “barremos” todas las unidades de los conglomerados seleccionados. Es decir que el conglomerado “j” lo elegimos con probabilidad Mj/M. ¿Cómo se hace? Se forma la suma acumulativa de las Mj y se forman intervalos con extremos en los acumulados consecutivos, elegido un número al azar se observa a qué conglomerado de la lista corresponde.

Muestreo por conglomerados mono-etápico (5) • Ejemplo: Conglomerado Tamaño (Mj) Σ Mj Rango asignado 1 20 20 1 -20 2 10 30 21 -30 3 45 75 31 -75 4 67 142 76 -142 5 50 192 143 -192 6 16 208 193 -208 7 25 233 209 -233 8 13 246 234 -246 Seleccionamos números al azar entre 1 y 246, sale por ejemplo el 123, entonces el conglomerado 4 es seleccionado y así sucesivamente, con reemplazo, es decir volvemos a sortear un número entre 1 y 246, sale por ejemplo el 78, el conglomerado 4 es nuevamente incluido, luego, en la tercera extracción obtenemos el 205, entra el conglomerado 6, etc.

Muestreo en varias etapas (sub-muestreo) • Concepto: La población se divide en grupos (conglomerados que son unidades primarias de muestreo: UPM), se muestrean conglomerados pero en lugar de “barrerlos” se selecciona una muestra de unidades del conglomerado (unidades secundarias de muestreo: USM), luego en una tercera etapa puede a su vez submuestrearse y así sucesivamente. • Es el diseño complejo más utilizado en las encuestas. • Pueden combinarse distintos diseños en las diferentes etapas

Muestreo en dos etapas (1) • Caso 1: M. A. S. en ambas etapas. Primera etapa: se eligen n UPM de las N con M. A. S. Primera etapa: se eligen mi USM con M. A. S de la i-ésima UPM seleccionada. Observación: se agrega ahora la varianza muestral entre USM dentro de las UPM. Estimadores: el total de la j-ésima UPM seleccionada se estimará por Y la media poblacional es insesgadamente estimada por: Varianza y estimador ver Notas § 2. 5. 2 fórmulas [40] y [41]

Muestreo en dos etapas (2) • Caso 2: UPM elegidas con ppt y USM con M. A. S En este caso un estimador insesgado del total es: y la estimación de la varianza se simplifica: Un caso particular muy utilizado en los muestreos agrícolas es el muestreo de áreas.

Caso particular: Muestreo de áreas. • Concepto: Las UPM son áreas contiguas de terreno (por ejemplo segmentos censales o subdivisiones de ellos). Se estratifican (por ejemplo, por uso del suelo) y se seleccionan ppt (con reposición). Luego las UPM seleccionadas se segmentan (el tamaño del segmento está en función del estrato) y se selecciona UN segmento al azar (M. A. S) por UPM sorteada. Esta forma de proceder simplifica mucho las cosas como veremos en la siguiente diapositiva.

Muestreo de áreas Asignada la UPM a su estrato y definido el tamaño que tendrán todos los segmentos de estrato queda determinado el número de segmentos (aproximado) de cada UPM. Sea Mjh el número de segmentos de la j-ésima UPM del estrato h, en la población. En la primera etapa elegimos la muestra de UPM con probabilidad proporcional al número de segmentos: Mjh /Mh luego en la UPM seleccionada elegimos 1 segmento aleatoriamente. ¿Cuál es la probabilidad de inclusión de un segmento del estrato h en la muestra? Pr(segmento sea seleccionado/salió la UPM)x. Pr(UPM) = (1/Mjh)x(Mjh /Mh )=1/Mh es decir es igual a sacar 1 segmento del total de segmentos del estrato. Y esto simplifica mucho las cosas. VER: FAO: “Encuestas Agrícolas con Múltiples Marcos de Muestreo”. Vol 1. (Cap 4)

Muestreo sistemático (1) • Sólo la primera unidad es seleccionada aleatoriamente y luego se elige una cada “tantas” hasta completar las n. Si la población tiene N unidades y k=N/n, elegimos aleatoriamente un número entre 1 y k y luego una de cada k.

Muestreo sistemático (2) Propiedades: 1)es un diseño EPSEM ya que cada unidad tiene la misma probabilidad de ser seleccionada (aunque no es equivalente al M. A. S. ). 2) Puede tratarse como un diseño por conglomerados donde elegimos un conglomerado de k conglomerados posibles o como un diseño estratificado en n estratos y elegimos una unidad de cada uno. 3) No se puede estimar insesgadamente la varianza. 4) Cuando k no es entero hay que usar “muestreo sistemático circular” 5) Es muy simple y cuando la correlación entre las unidades disminuye con la distancia entre ellas es muy eficiente.

Elección de un diseño • Elementos a considerar: 1) Presupuesto 2) Facilidades computacionales 3) Personal capacitado disponible 4) Información de base 5) Marcos disponibles y costo de elaboración/actualización 6) Niveles de precisión requeridos 7) Nivel de desagregación de los datos

Estimación de la varianza(1) A fin de calcular el error de muestreo (en cualquier diseño) es necesario estimar la varianza muestral de los estimadores. En algunos casos ello no es posible, por ejemplo en el muestreo sistemático usual. En otros no hay una expresión algebraica para la varianza estimada o ésta es muy compleja. Por ello se han diseñado diversos métodos para estimarla. Los paquetes estadísticos más usados en general incorporan alguno de ellos.

Estimación de la varianza(2) Algunos métodos: • Linearización: Estimadores no lineales, se aproximan por el desarrollo en series de Taylor y se desechan los términos mayores a los de primer orden. Caso más común: estimación de la varianza de estimadores de razón. • Grupos aleatorios (Muestreo replicado): La muestra total de n se divide en R grupos (de tamaño n/R), de manera que cada grupo es una versión “en pequeño” de toda la encuesta. Si las muestras de cada grupo son independientes, y siendo el parámetro estimado por la r-ésima muestra, se demuestra que un estimador insesgado de la varianza de es: » Caso más común: estimación de la varianza en el muestreo sistemático (con R arranques aleatorios).

Estimación de la varianza(3) • Replicas balanceadas (BBR): La muestra se divide en H estratos con 2 unidades por estrato. Hay 2 H maneras de elegir una submuestra de tamaño H con una unidad por estrato. Se toman R de estas muestras asignado los valores 1 y -1 a cada unidad en cada estrato. Cada submuestra así obtenida es un vector (αr ) de H componentes 1 y -1 que corresponden a H unidades “etiquetadas” con 1 y -1. Se eligen aquellos que sean ortogonales 2 a 2. Siendo el estimador de θ para el r -ésimo vector, una estimación de la varianza es: siendo

Estimación de la varianza(4) • Jacknife: La muestra se divide aleatoriamente en k grupos de m observaciones cada uno (n=mk). Se estima el parámetro con toda la muestra ( ) y con las unidades de k-1 grupos (se omite el grupo α-ésimo). Sea y entonces un estimador de la varianza es: • Bootstrap: Como las anteriores es una técnica de remuestreo donde R muestras independientes de tamaño n con reposición son independientemente extraídas de la muestra de n original y se producen R estimaciones y se estima la varianza entre elllas.

Software Todos los métodos de estimación de la varianza son muy intensivos en cálculo y requieren de paquetes específicos. Dentro de los paquetes estadísticos más comunes los métodos incorporados son: SAS: Linearización Stata: Linearización SUDAAN (software desarrollado para el análisis de diseños complejos) : Linearización, Jacknife, BRR, Bootstrap Osiris (para Mac): BRR y Jacknife R: Linearización, Jacknife, BRR, Bootstrap

Muchas gracias