RELAES Temas a tratar Relaes de ordem parcial
























- Slides: 26

RELAÇÕES

Temas a tratar: Relações de ordem parcial Relações de ordem total Conjuntos parcialmente ordenados e suas propriedades

Definição 1: Seja A um conjunto e R uma relação binária sobre A: ü R diz-se reflexiva quando x A, x. Rx; ü R diz-se simétrica quando x, y A (x. Ry y. Rx); ü R diz-se anti-simétrica quando x, y A (x. Ry e y. Rx x=y); ü R diz-se transitiva quando x, y, z A (x. Ry e y. Rz x. Rz); ü R diz-se dicotómica quando x, y A, x. Ry ou y. Rx; ü R diz-se tricotómica quando x, y A, se tem um e um só dos seguintes casos: x. Ry ou y. Rx ou x=y.

Definição 2: Seja A um conjunto e R uma relação binária sobre A. R diz-se uma relação de ordem parcial quando é reflexiva, anti-simétrica e transitiva. Definição 3: Seja A um conjunto e R uma relação binária sobre A. R diz-se uma relação de ordem total se for transitiva e tricotómica.

Exercício 1: Prove que se for uma relação de ordem total num conjunto A, então a relação , definida em A por x y ou x=y, é uma relação de ordem parcial.

Definição 4: Quando R é uma relação de ordem parcial num conjunto A, dizemos que (A; R) é um conjunto parcialmente ordenado (abreviadamente, cpo).

Exemplos: Os seguintes pares são cpo’s: 1) (P(A); ) onde A é um conjunto e P(A) representa o conjunto das partes (ou subconjuntos) de A. 2) (IN; ≤), (Z; ≤), (Q; ≤) e (IR; ≤), onde ≤ é a ordem usual. 3) (C; *) onde a relação * é definida, para quaisquer x, y, z, w IR, por (x yi) * (z wi) x z e y w.

Exercício 2: Prove que (IN; ) é um cpo, onde é a relação “é divisor de” em IN, isto é, para n, m IN tem-se n m m=kn, para algum k IN. Note-se no entanto que (Z; ), onde é a relação “é divisor de” em Z, ou seja, está definida para cada n, m Z por n m m=kn para algum k Z, não é um cpo. De facto, não é uma relação anti-simétrica pois 2 -2, -2 2 e, no entanto, 2 -2.

Notação: Habitualmente é usado o símbolo para representar uma ordem parcial num conjunto A. Dados x, y A, escreve-se: • x y e diz-se que “x é menor ou igual a y”; • x y se x y e, diz-se que “x é menor que y”; • x y para negar x y, e diz-se que “x não é menor nem igual a y”;

• x y se y x, e diz-se que “x é maior ou igual a y”; • x<<y se x y e z A tal que x z y e diz-se que “x é coberto por y” ou que “y cobre x”; • x y se x y e y x, e diz-se que "x e y são incomparáveis”. Por exemplo, 4 6 em (IN; ), 6<<7 em (IN; ), e não existem x, y IR tais que x<<y em (IR; ).

Definição 5: Se R é uma relação binária sobre A, a relação binária R-1 sobre A definida, para cada x, y A, por x R-1 y y R x é chamada a relação inversa de R. Se (A; ) é um cpo, então representa a relação inversa (também chamada a relação dual) de e (A; ) é um cpo, chamado o cpo dual de (A; ).

Definição 6: Seja (A; ) um cpo e seja X um subconjunto de A. Por restrição da relação a X obtém-se uma relação de ordem parcial em X (relação induzida pela relação em A). Assim, (X; ) é um cpo para a relação induzida pela relação de (A; ). Definição 7: Seja (A; ) um cpo. Diz-se que (A; ) é um conjunto totalmente ordenado ou uma cadeia, se quaisquer dois elementos estiverem relacionados, isto é, dados x, y A, tem-se x y ou y x. Neste caso, os elementos x e y dizem -se comparáveis.

Exemplos: 1. Os cpo’s (IN; ), (Z; ), (Q; ) e (IR; ) com a operação “ ” usual, são cadeias. 2. Dado um conjunto A, o cpo (P(A); ) não é uma cadeia. Por exemplo, se considerarmos A={1, 2, . . . , 12}, os dois elementos {1} e {2} são incomparáveis, uma vez que {1} {2} e {2} {1}.

Um cpo finito (A; ) pode ser representado graficamente por um diagrama, chamado diagrama de Hasse. Num tal diagrama, um ponto ou pequeno círculo que represente um certo elemento x deve ser desenhado abaixo de qualquer ponto que represente um elemento y tal que x y. Se x e y são elementos tais que x y, então desenha -se um segmento de recta unindo o ponto que representa x ao ponto que representa y.

Por exemplo, considere-se o cpo (P(A); ), com A IN finito. Apresentam-se a seguir, diagramas de Hasse para alguns cpo’s deste tipo: (i) (P({1}); ) {1}

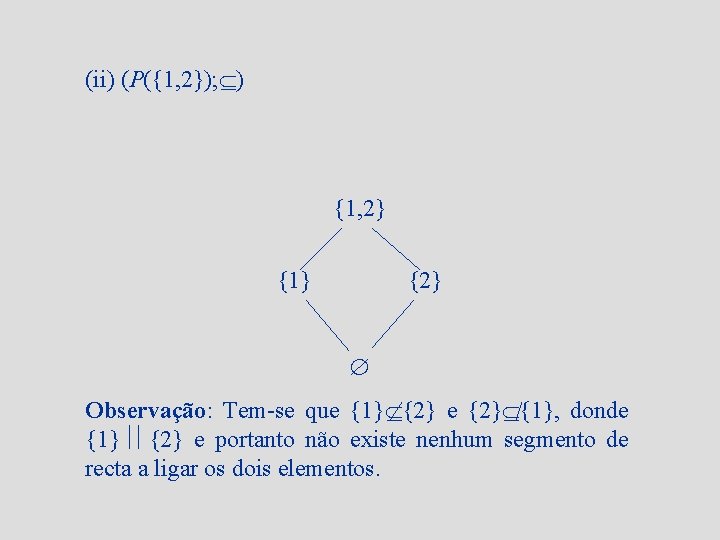
(ii) (P({1, 2}); ) {1, 2} {1} {2} Observação: Tem-se que {1} {2} e {2} {1}, donde {1} {2} e portanto não existe nenhum segmento de recta a ligar os dois elementos.


Exercício 3: No conjunto A={1, 2, 3, 4, . . . , 12} a relação de “divisor” é uma relação de ordem parcial. Recorda-se que, para x, y A, dizer que “x é divisor de y” ou "x divide y" ou "x y" significa que k A, tal que, y = x. k Construa o diagrama de Hasse para o cpo (A; ).

Definição 8: Sejam (A; ) um cpo e X A. Diz-se que: Ø m X é elemento maximal em X se x X (m x m=x); Ø n X é elemento minimal em X se x X (x n x=n); Ø m X é elemento máximo de X se x X, x m; Ø n X é elemento mínimo de X se x X, n x; Ø m A é majorante de X se x X, x m; Ø n A é minorante de X se x X, n x;

Øs A é supremo de X se: - x X, x s; - x X, x m s m; Øt A é ínfimo de X se: - x X, t x; - x X, n x n t.

Notação: Ma X – conjunto dos majorantes de X; Mi X – conjunto dos minorantes de X; X ou sup X – supremo de X; X ou inf X – ínfimo de X; max X – elemento máximo de X; min X – elemento mínimo de X. Observação: A anti-simetria da relação garante que, no caso de existir elemento máximo (elemento mínimo, supremo, ínfimo) de X, este é único.

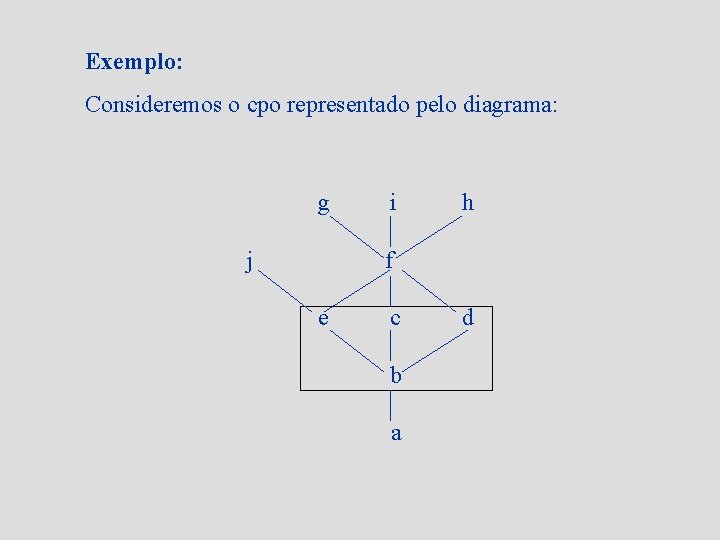
Exemplo: Consideremos o cpo representado pelo diagrama: g j i h f e c b a d

Se X={b, c, d, e}, tem-se: Mi X = {a, b} Ma X = {g, i, h, f} Sup X = f Inf X = b Min X = b Max X - não existe porque, f X e f é o menor dos majorantes. Maximais em X = {e, c, d} Minimais em X = {b}

Observações: Um subconjunto dum cpo pode admitir mais do que um elemento maximal (resp. minimal); Um subconjunto dum cpo pode não admitir elementos maximais (resp. minimais). Por exemplo, Z com a relação usual “ ”; Se existir elemento máximo (resp. mínimo) de um subconjunto X dum cpo (A; ), ele é elemento maximal em X (resp. minimal)

Exemplo: No diagrama de Hasse seguinte está representado um cpo que tem 3 elementos maximais mas não tem elemento máximo. a b c d e

Exercício 4: Considere-se o cpo (A; ), com A = {1, 2, . . . , 12}. Seja X={1, 2, 3, 4, 6, 8, 12} tal que X A. Represente por um diagrama de Hasse o cpo (A; ). Indique, caso existam: Ma X, Mi X, Sup X, Inf X, Min X, Max X, elementos maximais e minimais em X.
 Relação de ordem
Relação de ordem Dislasia
Dislasia Numero necesario a tratar
Numero necesario a tratar Tratar dislasias
Tratar dislasias Coma mixedematoso tratamiento
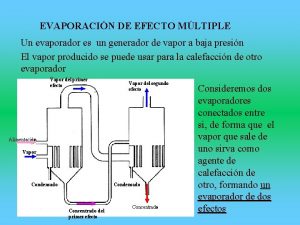
Coma mixedematoso tratamiento Evaporador doble efecto contracorriente
Evaporador doble efecto contracorriente Propiltiouracilo
Propiltiouracilo Valor de p
Valor de p Elizabeta tratar pirc
Elizabeta tratar pirc Cariotipo mola completa
Cariotipo mola completa Buccinador
Buccinador Dsav parcial
Dsav parcial Aseo parcial
Aseo parcial Modelo entidad relacion herencia
Modelo entidad relacion herencia Organigrama parcial
Organigrama parcial Correlacion semiparcial
Correlacion semiparcial Certificado de licenciatura
Certificado de licenciatura Cisão parcial contabilização
Cisão parcial contabilização Pressao parcial
Pressao parcial Npp esteroide
Npp esteroide Quejoso amparo
Quejoso amparo Semiparcial
Semiparcial Derivada parcial
Derivada parcial Soporte ventilatorio parcial
Soporte ventilatorio parcial Superposicion parcial de objetos iguales
Superposicion parcial de objetos iguales Retenedor doble acker
Retenedor doble acker Corrección de tiempo de protrombina
Corrección de tiempo de protrombina