Production Function l The firms production function for

Production Function l The firm’s production function for a particular good (q) shows the maximum amount of the good that can be produced using alternative combinations of capital (K) and labor (L) q = f (K , L )

Marginal Physical Product l To study variation in a single input, we define marginal physical product as the additional output that can be produced by employing one more unit of that input while holding other inputs constant

Diminishing Marginal Productivity The marginal physical product of an input depends on how much of that input is used l In general, we assume diminishing marginal productivity l

Diminishing Marginal Productivity Because of diminishing marginal productivity, 19 th century economist Thomas Malthus worried about the effect of population growth on labor productivity l But changes in the marginal productivity of labor over time also depend on changes in other inputs such as capital. l

Average Physical Product l Labor productivity is often measured by average productivity l Note that APL also depends on the amount of capital employed

A Two-Input Production Function l Suppose the production function for flyswatters can be represented by q = f(K, L) = 600 K 2 L 2 - K 3 L 3 l To construct MPL and APL, we must assume a value for K l Let l K = 10 The production function becomes q = 60, 000 L 2 - 1000 L 3

A Two-Input Production Function l The marginal productivity function is MPL = q/ L = 120, 000 L - 3000 L 2 which diminishes as L increases l This implies that q has a maximum value: 120, 000 L - 3000 L 2 = 0 40 L = L 2 L = 40 l Labor input beyond L=40 reduces output

A Two-Input Production Function l To find average productivity, we hold K=10 and solve APL = q/L = 60, 000 L - 1000 L 2 l APL reaches its maximum where APL/ L = 60, 000 - 2000 L = 0 L = 30

A Two-Input Production Function l In fact, when L=30, both APL and MPL are equal to 900, 000 l Thus, when APL is at its maximum, APL and MPL are equal

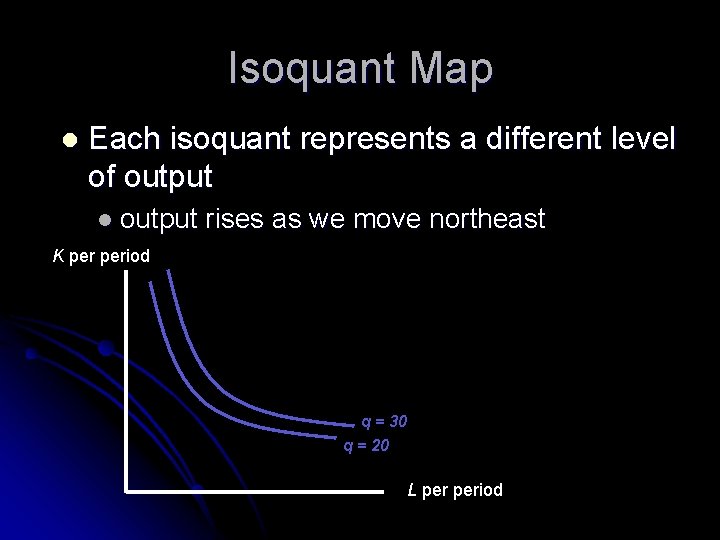
Isoquant Maps To illustrate the possible substitution of one input for another, we use an isoquant map l An isoquant shows those combinations of K and L that can produce a given level of output (q 0) l f (K , L ) = q 0

Isoquant Map l Each isoquant represents a different level of output l output rises as we move northeast K period q = 30 q = 20 L period

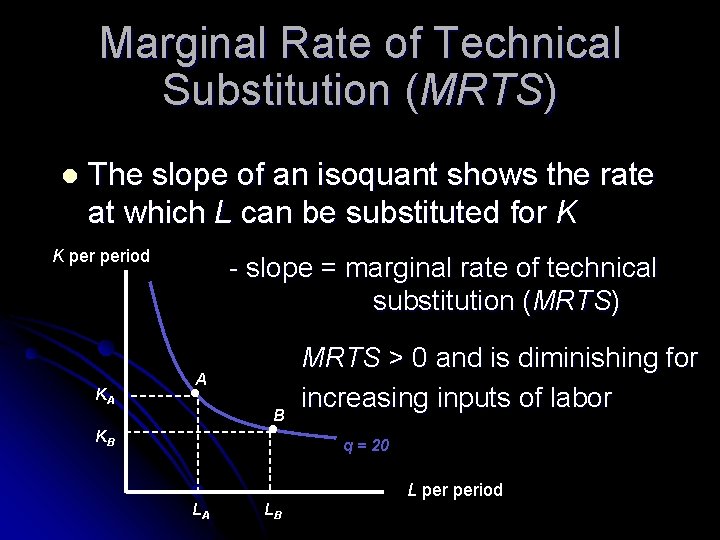
Marginal Rate of Technical Substitution (MRTS) l The slope of an isoquant shows the rate at which L can be substituted for K K period KA - slope = marginal rate of technical substitution (MRTS) A B KB MRTS > 0 and is diminishing for increasing inputs of labor q = 20 L period LA LB

Returns to Scale How does output respond to increases in all inputs together? l Suppose that all inputs are doubled, would output double? l Returns to scale have been of interest to economists since the days of Adam Smith l

Returns to Scale l Smith identified two forces that come into operation as inputs are doubled l greater division of labor and specialization of labor l loss in efficiency because management may become more difficult given the larger scale of the firm

Returns to Scale l If the production function is given by q = f(K, L) and all inputs are multiplied by the same positive constant (m > 1), then

Returns to Scale l It is possible for a production function to exhibit constant returns to scale for some levels of input usage and increasing or decreasing returns for other levels l economists refer to the degree of returns to scale with the implicit notion that only a fairly narrow range of variation in input usage and the related level of output is being considered

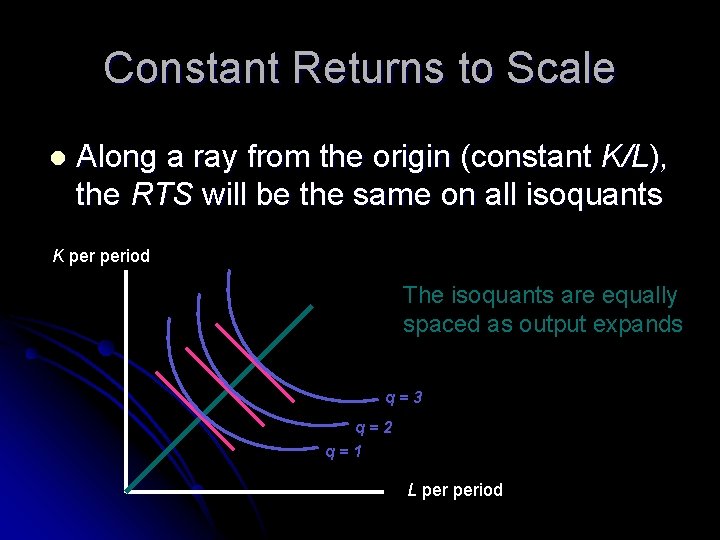
Constant Returns to Scale l Constant returns-to-scale production functions have the useful theoretical property that the MRTS between K and L depends only on the ratio of K to L, not the scale of operation l Geometrically, all of the isoquants are “radial blowups” of the unit isoquant

Constant Returns to Scale l Along a ray from the origin (constant K/L), the RTS will be the same on all isoquants K period The isoquants are equally spaced as output expands q=3 q=2 q=1 L period

Returns to Scale l Returns to scale can be generalized to a production function with n inputs q = f(X 1, X 2, …, Xn) l If all inputs are multiplied by a positive constant m, we have f(m. X 1, m. X 2, …, m. Xn) = mkf(X 1, X 2, …, Xn)=mkq l If k=1, we have constant returns to scale l If k<1, we have decreasing returns to scale l If k>1, we have increasing returns to scale

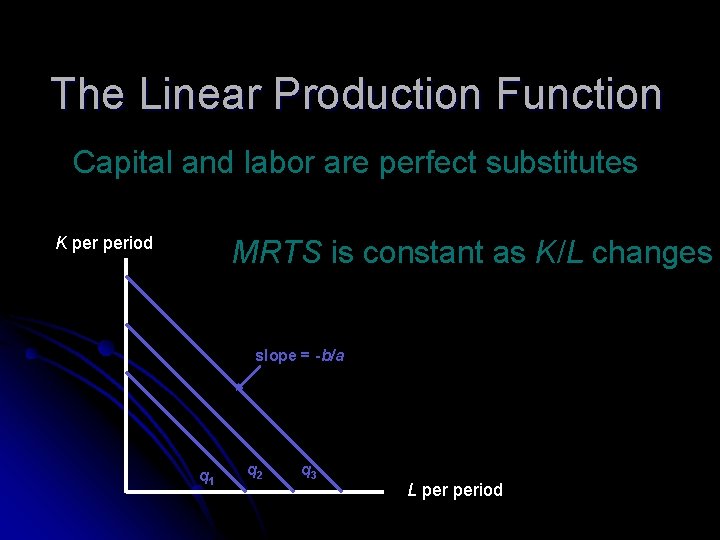
The Linear Production Function l Suppose that the production function is q = f(K, L) = a. K + b. L l This production function exhibits constant returns to scale f(m. K, m. L) = am. K + bm. L = m(a. K + b. L) = mf(K, L) l All isoquants are straight lines l MRTS is constant

The Linear Production Function Capital and labor are perfect substitutes K period MRTS is constant as K/L changes slope = -b/a q 1 q 2 q 3 L period

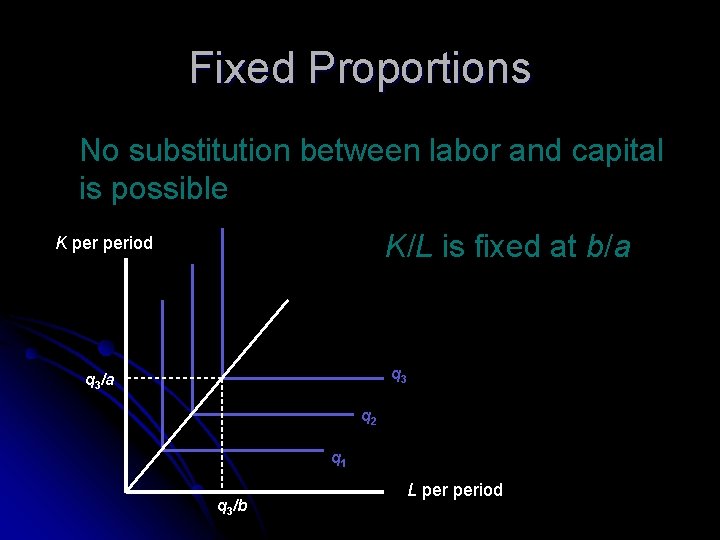
Fixed Proportions No substitution between labor and capital is possible K/L is fixed at b/a K period q 3/a q 2 q 1 q 3/b L period

Cobb-Douglas Production Function l Suppose that the production function is q = f(K, L) = AKa. Lb A, a, b > 0 l This production function can exhibit any returns to scale f(m. K, m. L) = A(m. K)a(m. L) b = Ama+b Ka. Lb = ma+bf(K, L) l if a + b = 1 constant returns to scale l if a + b > 1 increasing returns to scale l if a + b < 1 decreasing returns to scale

Cobb-Douglas Production Function l Suppose that hamburgers are produced according to the Cobb-Douglas function q = 10 K 0. 5 L 0. 5 Since a+b=1 constant returns to scale l The isoquant map can be derived l q = 50 = 10 K 0. 5 L 0. 5 KL = 25 q = 100 = 10 K 0. 5 L 0. 5 KL = 100 l The isoquants are rectangular hyperbolas

Cobb-Douglas Production Function l The MRTS can easily be calculated The MRTS declines as L rises and K falls l The MRTS depends only on the ratio of K and L l