The Production Process Production Analysis Production Function Q

The Production Process

Production Analysis • Production Function Q = f(K, L) • Describes available technology and feasible means of converting inputs into maximum level of output, assuming efficient utilization of inputs: • ensure firm operates on production function (incentives for workers to put max effort) • use cost minimizing input mix • Short-Run vs. Long-Run Decisions • Fixed vs. Variable Inputs

Total Product • Cobb-Douglas Production Function • Example: Q = f(K, L) = K. 5 L. 5 • K is fixed at 16 units. • Short run production function: Q = (16). 5 L. 5 = 4 L. 5 • Production when 100 units of labor are used? Q = 4 (100). 5 = 4(10) = 40 units

Marginal Product of Labor • Continuous case: MPL = d. Q/d. L • Discrete case: arc MPL = Q/ L • Measures the output produced by the last worker. • Slope of the production function

Average Product of Labor • APL = Q/L • Measures the output of an “average” worker. • Slope of the line from origin onto the production function

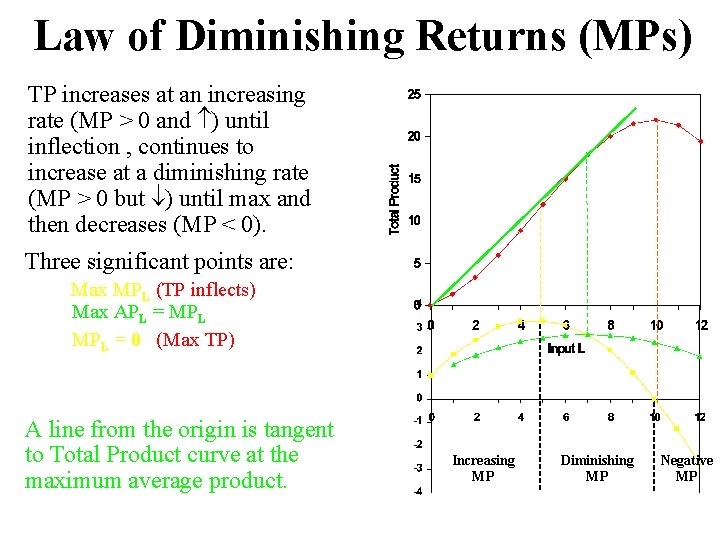
Law of Diminishing Returns (MPs) TP increases at an increasing rate (MP > 0 and ) until inflection , continues to increase at a diminishing rate (MP > 0 but ) until max and then decreases (MP < 0). Three significant points are: Max MPL (TP inflects) Max APL = MPL = 0 (Max TP) A line from the origin is tangent to Total Product curve at the maximum average product. Increasing MP Diminishing MP Negative MP

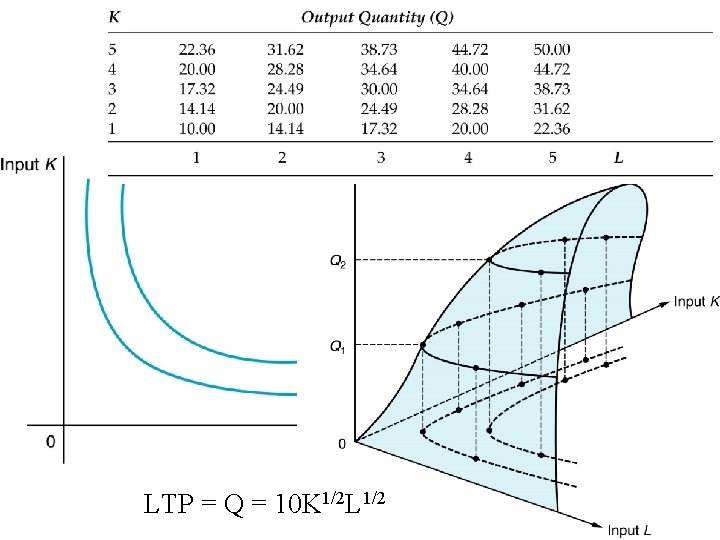
LTP = Q = 10 K 1/2 L 1/2

Isoquant • The combinations of inputs (K, L) that yield the producer the same level of output. • The shape of an isoquant reflects the ease with which a producer can substitute among inputs while maintaining the same level of output. • Slope or Marginal Rate of Technical Substitution can be derived using total differential of Q=f(K, L) set equal to zero (no change in Q along an isoquant)

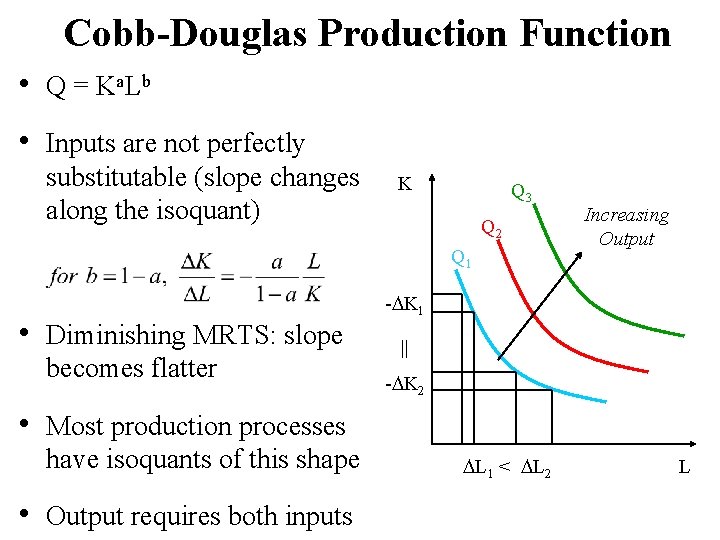
Cobb-Douglas Production Function • Q = K a. L b • Inputs are not perfectly substitutable (slope changes along the isoquant) K Q 3 Q 2 Q 1 • Diminishing MRTS: slope becomes flatter Increasing Output - K 1 || - K 2 • Most production processes have isoquants of this shape • Output requires both inputs L 1 < L 2 L

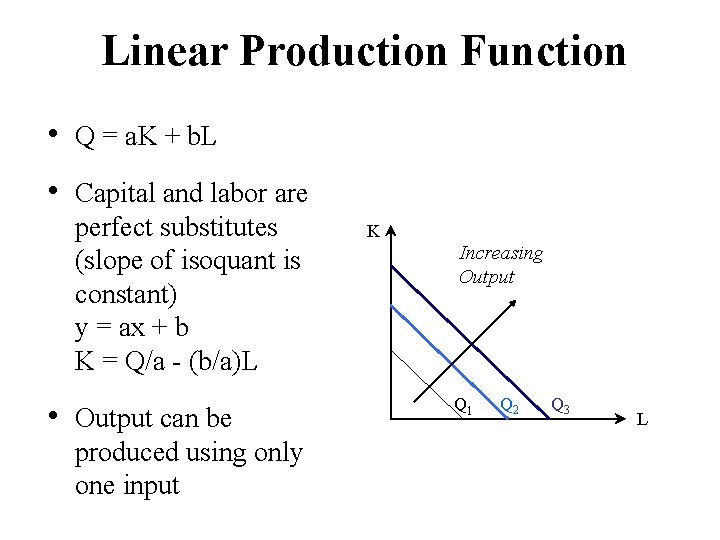
Linear Production Function • Q = a. K + b. L • Capital and labor are perfect substitutes (slope of isoquant is constant) y = ax + b K = Q/a - (b/a)L • Output can be produced using only one input K Increasing Output Q 1 Q 2 Q 3 L

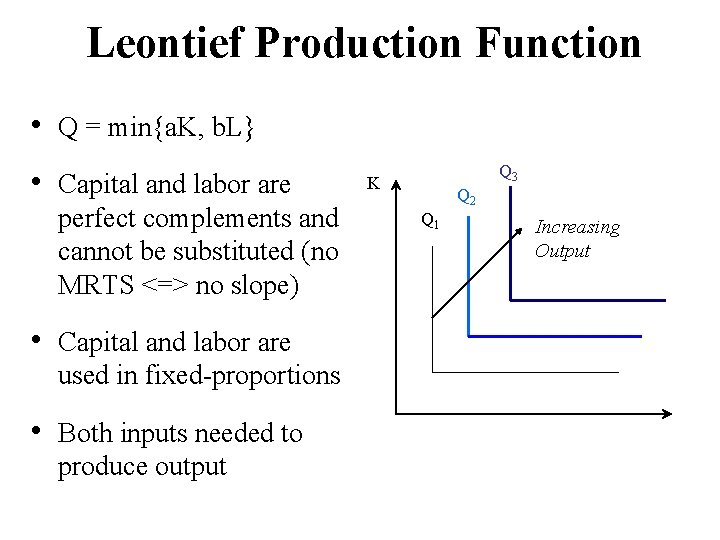
Leontief Production Function • Q = min{a. K, b. L} • Capital and labor are perfect complements and cannot be substituted (no MRTS <=> no slope) • Capital and labor are used in fixed-proportions • Both inputs needed to produce output Q 3 K Q 2 Q 1 Increasing Output

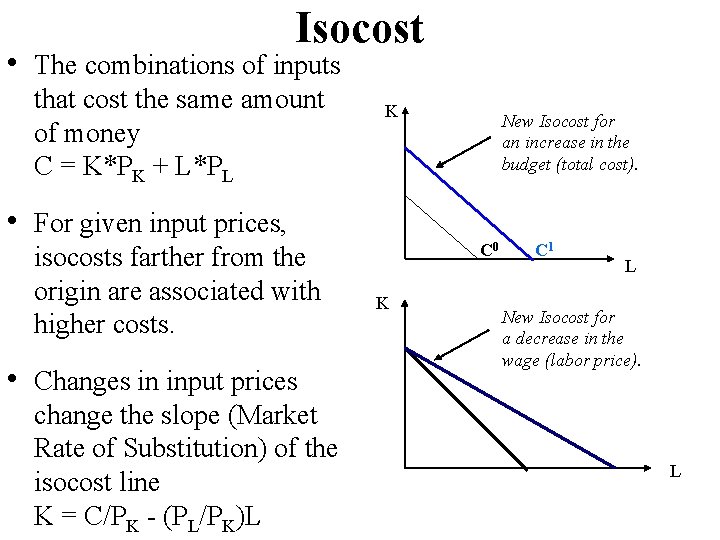
Isocost • The combinations of inputs that cost the same amount of money C = K*PK + L*PL K New Isocost for an increase in the budget (total cost). • For given input prices, isocosts farther from the origin are associated with higher costs. • Changes in input prices change the slope (Market Rate of Substitution) of the isocost line K = C/PK - (PL/PK)L C 0 K C 1 L New Isocost for a decrease in the wage (labor price). L

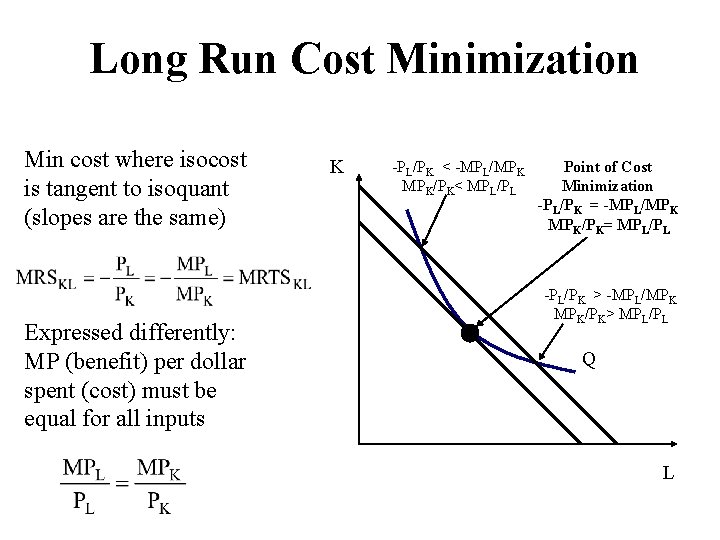
Long Run Cost Minimization Min cost where isocost is tangent to isoquant (slopes are the same) Expressed differently: MP (benefit) per dollar spent (cost) must be equal for all inputs K -PL/PK < -MPL/MPK MPK/PK< MPL/PL Point of Cost Minimization -PL/PK = -MPL/MPK MPK/PK= MPL/PL -PL/PK > -MPL/MPK MPK/PK> MPL/PL Q L

Returns to Scale • Return (MP): How TP changes when one input increases • RTS: How TP changes when all inputs increase by the same multiple > 0 • Q = f(K, L) • • Q = 50 K½L½ Q = 100, 000 + 500 L + 100 K Q = 0. 01 K 3 + 4 K 2 L + L 2 K + 0. 0001 L 3