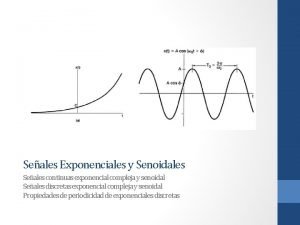
Procesamiento de Seales Profesores Vicente Mut INAUT Luis

Procesamiento de Señales Profesores: Vicente Mut (INAUT) Luis Romero (GATEME) Dictado de Clases: Miércoles de 8 a 13 hs

Temas: n Señales, Sistemas y Convolución n Muestreo, Transformada de Fourier y Transformada Z n Filtros Analógicos n Filtros Digitales

Objetivos del Curso - Dar a los alumnos una comprensión de los conceptos de Señales y Sistemas de tiempo discreto. - Dar a los estudiantes una comprensión de las transformadas Z y de Fourier y sus inversas. - Dar a los estudiantes una comprensión de la relación entre Funciones de un sistema, Ecuaciones en diferencia y Filtros digitales. - Dar a los estudiantes conocimientos acerca de las apliaciones mas importantes de muestreo y reconstrucción de señales - Hacer que los estudiantes sean capaces de aplicar filtros digitales de acuerdo a las especificaciones conocidas de un filtro. - Proporcionar conocimientos acerca de los principios de la Transformada de Fourier Discreta (DFT) y su cálculo rápido - Hacer que los estudiantes pueden aplicar el análisis de Fourier de señales estocásticas usando la DFT - Ser capaz de aplicar el programa MATLAB a los problemas de procesamiento digital. - Ser capaz de implementar en un DSP (Procesador de Señales Digitales) los problemas de procesamiento digital (Análisis de Señales, Filtros Digitales, etc. ).

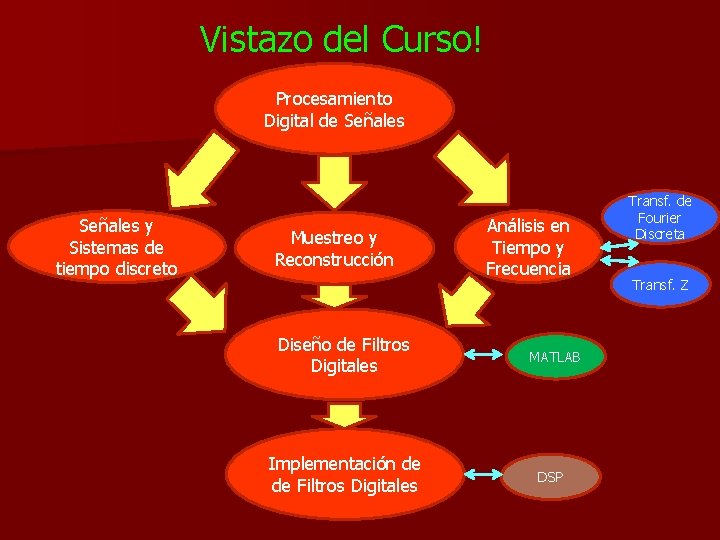
Vistazo del Curso! Procesamiento Digital de Señales y Sistemas de tiempo discreto Muestreo y Reconstrucción Diseño de Filtros Digitales Implementación de Filtros Digitales Análisis en Tiempo y Frecuencia MATLAB DSP Transf. de Fourier Discreta Transf. Z

Que es una señal? - Un flujo de información. - Matematicamente representada como una función de variable independiente como el tiempo (por ej. Señal de voz), position (por ej imágen), etc. - Una convención establece a la variable independiente como el tiempo Señales ejemplo - Voz: Señal Unidimensional función del tiempo s(t); - Imágen en escala de grises: Señal de 2 dimensiones como función espacial i(x, y) - Video: Señal de 3 dimensiones como una función del espacio y el tiempo {r(x, y, t), g(x, y, t), b(x, y, t)}.

Bibliografía -Apuntes de cátedra n -PROCESAMIENTO DE SEÑALES ANALOGICAS Y DIGITALES. A. Ambardar. 2 da. Edición, Thomson Learning, 2006. n -"Analog and Digital Signal Processing". (1998). Ambardar A. , PWS Publishing Company. n - “System Analysis & Signal Processing”, 1998, P. Denbigh, Addison-Wesley. n -“Digital Signal Processing”, M. Heyes, 1999, Schaum´s Outlines. n -“Understanding Digital Signal Processing”, 2010, R. Lyons, Addison Wesley. n -"Digital Signal Processing". (1987). Roberts R. & Mullis C. . Addison-Wesley. n -"Sistemas Controlados por Computador". (1988). Astrom K. . Paraninfo. n - “Computer-Controlled Systems: Theory and Design”, Third Edition. 2011. Karl Johan Åström, Bjorn Wittenmark. n -“Señales y Sistemas”, Oppenheim, Willsky, Peason Eductation, 1998. n -"Adaptive Signal Processing". (1985). Widrow B. & Stearns L. . Prentice Hall. n -"Signal and Systems". (1986). Meade M. & Dillon C. . Van Nostrand Reinhold (UK). n - “Digital Signal Processing: Signals, Systems, and Filters”, Antoniou, A. , Mc. Graw-Hill, 2005 (966 pages). ISBN 0 -07 -145425 -X n Revistas especializadas: - IEEE Trans. and Magazine on Signal Processing. - IEEE Trans. on Education. - Otras publicaciones de IEEE. n

Forma de dictado n Clases teóricas n Clases prácticas: * Ocho laboratorios basados en Matlab * Una práctica de laboratorio integradora de filtros digitales con señales biomédicas reales

Forma de evaluación: Dos opciones 1) PROMOCIÓN -Evaluación con informe de prácticas de laboratorio en MATLAB. Se realizarán en forma grupal y calificará aprobado o reprobado, con fechas límites para su presentación de 15 días después de finalizada. La asistencia será obligatoria. -La última práctica tendrá carácter integradora y además del informe se hará una presentación oral grupal con calificación individual (aprobación con 7/10 puntos o mas). -Evaluación individual mediante dos pruebas parciales sobre temas teóricos y prácticos. Se dará la oportunidad de una recuperación por parcial. Se calificarán de 0 a 10. (aprobación con 7/10 puntos o mas). En caso de no presentar en tiempo el informe, o tener que realizar correcciones mayores, o ausencia no justificada en alguna de la prácticas, se deberán recuperar o corregir o hacer las practicas correspondientes, pero se pasa al sistema de evaluación 2). En caso de no obtener una calificación de 7/10 puntos en algún parcial y su recuperación, se pasa al sistema de evaluación 2)

Forma de evaluación: Dos opciones 2) REGULARIDAD CON EXAMEN FINAL -Evaluación con informe de prácticas de laboratorio en MATLAB. Idem a 1) -La última práctica tendrá carácter integradora y además del informe se hará una presentación oral grupal con calificación individual (aprobación con 5/10 puntos o mas) - Evaluación individual mediante dos pruebas parciales sobre temas teóricos y prácticos. Se calificarán de 0 a 10. Se dará la oportunidad de una recuperación por parcial y la oportunidad de una recuperación extraordinaria al finalizar el semestre. (aprobación con 5/10 puntos o mas) - Examen final. Examen en fechas normales fijadas por la Facultad.

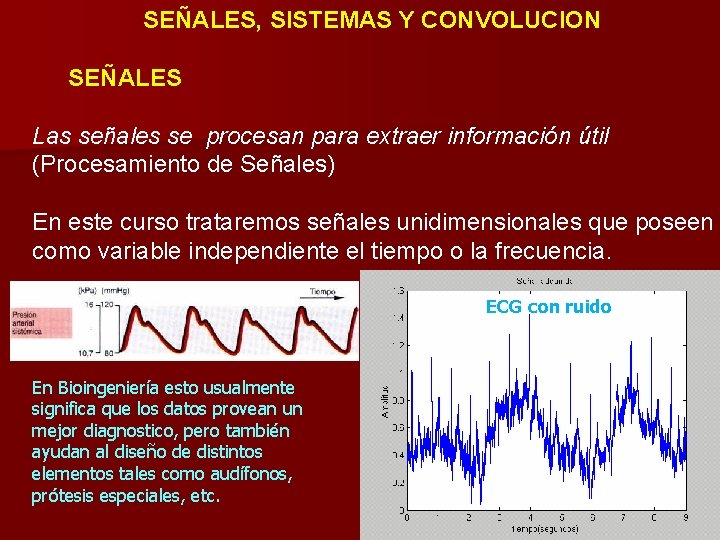
SEÑALES, SISTEMAS Y CONVOLUCION SEÑALES Las señales se procesan para extraer información útil (Procesamiento de Señales) En este curso trataremos señales unidimensionales que poseen como variable independiente el tiempo o la frecuencia. ECG con ruido En Bioingeniería esto usualmente significa que los datos provean un mejor diagnostico, pero también ayudan al diseño de distintos elementos tales como audífonos, prótesis especiales, etc.

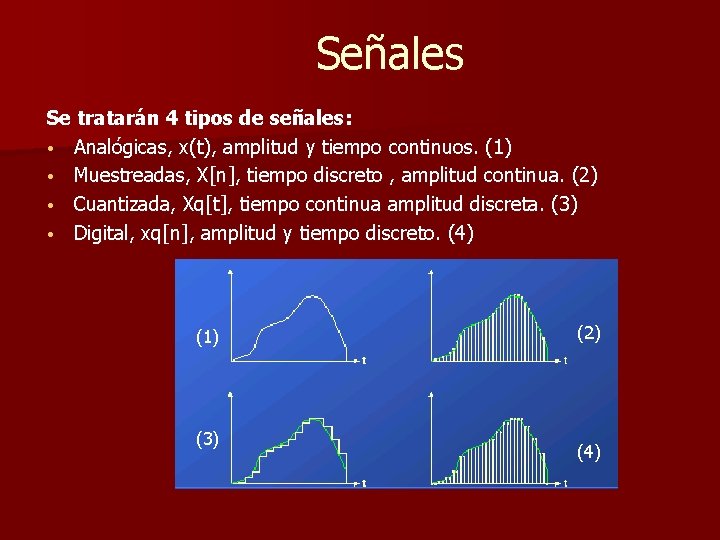
Señales Se tratarán 4 tipos de señales: • Analógicas, x(t), amplitud y tiempo continuos. (1) • Muestreadas, X[n], tiempo discreto , amplitud continua. (2) • Cuantizada, Xq[t], tiempo continua amplitud discreta. (3) • Digital, xq[n], amplitud y tiempo discreto. (4) (1) (3) (2) (4)

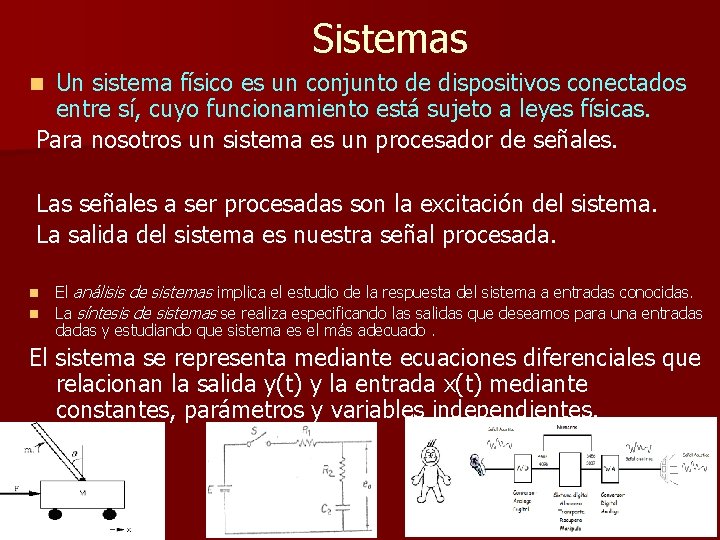
Algunas Señales mas utilizadas

Algunas Señales

EJEMPLOS DE SEÑAL EN MATLAB n = 0: 0. 5: 10; y = -3*n. *sin(2*n) dtplot(n, y) grid, title('Función Seno') % Arreglo temporal a intervalos de 0. 5 s % Valores de la Función % Gráfica % Grilla y títulos

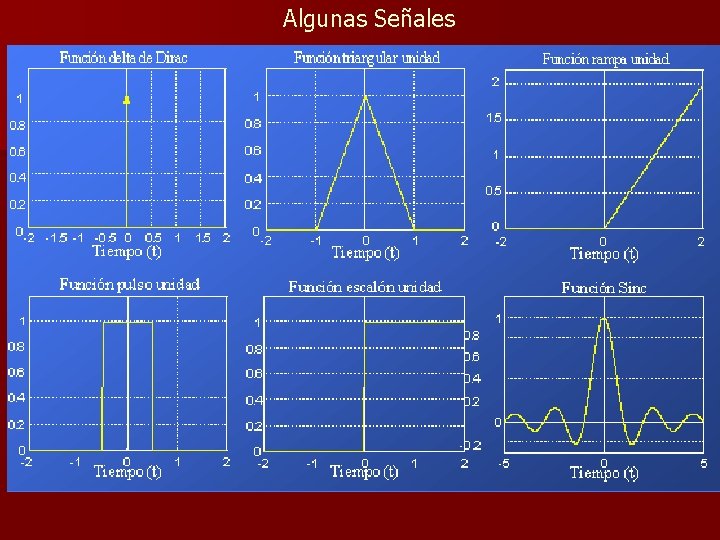
Operaciones con señales de tiempo discreto Suma: x[n]+y[n], suma punto de x[n] e y[n]. Producto: x[n]y[n], producto punto a punto de x[n] e y[n]. Desplazamiento en el tiempo: x[n-3], retarda x[n] 3 unidades de tiempo. Inversión: x[-n], invierte la señal original Escalamiento en amplitud: 3 x[n], multiplica la señal original por 3 Desplazamiento en amplitud: x[n]+3, suma un offset de CC de 3 a x[n]. Diezmado: x[2 n], comprime x[n] en un factor 2 (elimina muestras alternadas) Interpolación: x[n/2], amplia x[n] por un factor 2 (interpola entre dos muestras sucesivas) Combinaciones

Interpolar una señal por un factor k muestrear con ts/k. Además existen distintos tipos de interpolación: cero, escalón y lineal. La interpolación no es la inversa de la decimación, x[n]=1 2 6 4 8 dec. x[2 n]=1 6 8 interp. 1 1 6 6 8 8 El diezmado es la inversa de la interpolación x[n]=1 2 6 4 8 interp. x[n/2]=1 1 2 2 6 6 8 8 dec. x[n]=1 2 6 4 8

Clasificación de las señales según su duración n Causales: Son 0 para t<0. Se definen sólo para el eje positivo de t. n Anticausales: Son 0 para t>0. Se definen sólo para el eje negativo de t. n No causales: Se definen para ambos ejes de t. Continuas: Se definen para todo tiempo t. n Periódicas: xp(t) = xp(t±n. T), donde T es el periodo y n es un entero. Basada en la simetría n Simetría Par: x(t) = x(-t) n Simetría Impar: x(t) = -x(-t) n En energía y potencia (impulsos limitados en tiempo y señales periódicas) Energía de una señal : Potencia de una señal : Una señal se dice que es de energía si Ex es finito, lo que implica que Px es 0. Ej. Pulsos limitados en el tiempo. Una señal se dice que es de potencia si Px es finito, lo que implica que Ex es infinito. Ej. Una señal periódica.

Clasificación de señales basada en periodicidad y simetría Una señal es periódica si, x[n]=x[n k. N], con k= 0, 1, 2, . . . ; Fo=1/N, N es un entero. Una señal posee simetría: Par si Impar si xe[n]=xe[-n] xo[n]=-xo[-n] Partes pares e impares de un función: xe=1/2{x[n]+x[-n]} xo=1/2{x[n]-x[-n]} Señal par parte impar Señal impar

Representación de señales de tiempo discreto por impulsos de tiempo discreto. Las señales de tiempo discreto x[n] se pueden representar por una suma de desplazamientos de impulsos de tiempo discreto, [n-k], donde x[k]corresponde al valor de la señal en n=k. X[n]=. . . +x[-1] [n+1]+x[0] [n]+x[1] [n-1]+. . . = La representación del escalón de tiempo discreto seria, u[n]= Ej. x[n]={4, 2, 1, -3, 6}= 4 [n+1]+2 [n]+ [n-1]-3 [n-2]+ 6 [n-3] -1 0 1 1 2

Función sinc de tiempo de discreto La función sinc es una de las funciones mas importantes dentro del Procesamiento de señales, y esta definida, Sinc(n/N)=sen(n /N)/(n /N) Observaciones: sinc (n/N)=0, n=k. N, k= 1, 2, . . . sinc (n)= [n]

Señal Sinc n Se define la señal sinc como:

DEFINICIONES Frecuencia digital Existe un parámetro muy importante en el análisis de señales de tiempo discreto denominado Frecuencia Digital y la cual se define en función del período de muestreo utilizado para obtener la señal discreta a partir de una señal continua. Frecuencia digital F=f/Sf donde Sf=1/ts es la frecuencia de muestreo, además =2 F es la frecuencia digital angular.

Periodicidad y Frecuencia de señales armónicas de tiempo discreto. En señales de tiempo discreto no todas las armónicas de una señal periódica son periódicas. x[n]=e(j 2 Fn) , x[n+N]= e(j 2 F(n+N)) = e(j 2 Fn) e(j 2 FN) =1 si FN=entero Por lo tanto para que exista periodicidad se debe cumplir que FN=k=entero, las armónicas de tiempo discreto son periódicas si F=f/Sf es una fracción racional de la forma k/N. Por ej. x[n]=cos(2 n /16) es una señal periódica de período N=16 x[n]=cos(n/2), 2 n F=n/2 F=1/4 , número no racional, por lo tanto x[n] es no periódica. Observaciones Si F es una función no racional no hay periodicidad

Rango principal de una señal Si se considera una sinusoide de tiempo discreto x[n]= cos(2 F n+ ), cuya frecuencia digital tiene una parte entera M y una parte fraccional Fr tal que Fr <1/2 entonces, x[n]=cos[2 (M+Fr)n+ ]=cos(2 Fr n+ ), si Fr es (-), x[n]= cos(-2 Fr n+ )= cos(2 Fr n- ) fase reversible. Ej. a) x[n]=cos[2 (10/3)n+ ], F=10/3, M=3, Fr=1/3, x[n]=cos[2 (1/3)n+ ] b) x[n]=cos[2 (8/3)n+ ], F=8/3, M=3, Fr=-1/3, x[n]=cos[-2 (1/3)n+ ], x[n]=cos[2 (1/3)n- ]

Sistemas Un sistema físico es un conjunto de dispositivos conectados entre sí, cuyo funcionamiento está sujeto a leyes físicas. Para nosotros un sistema es un procesador de señales. n Las señales a ser procesadas son la excitación del sistema. La salida del sistema es nuestra señal procesada. n n El análisis de sistemas implica el estudio de la respuesta del sistema a entradas conocidas. La síntesis de sistemas se realiza especificando las salidas que deseamos para una entradas dadas y estudiando que sistema es el más adecuado. El sistema se representa mediante ecuaciones diferenciales que relacionan la salida y(t) y la entrada x(t) mediante constantes, parámetros y variables independientes.

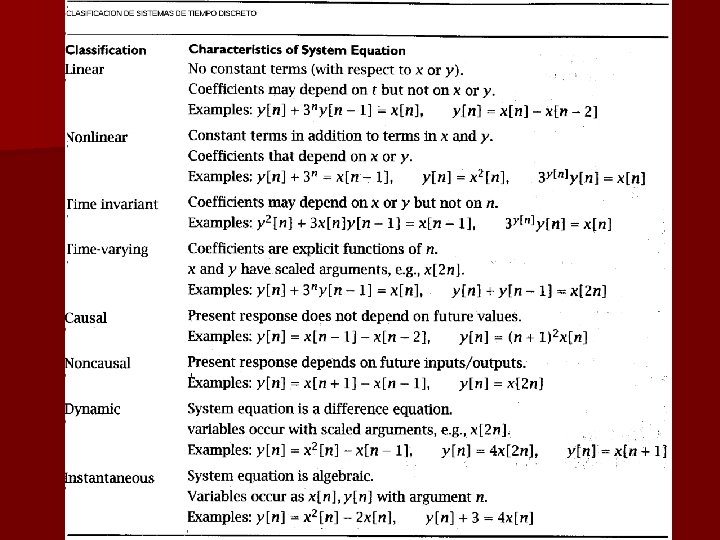
Sistemas: Clasificación Los sistemas se clasifican en : * Lineales: los coeficientes no dependen de x o y, no hay n términos constantes. * No lineales: los coeficientes dependen de x o y, hay términos constantes. * Invariante en el tiempo: Los coeficientes no dependen de t. • Variante en el tiempo: Los coeficientes son funciones de t. • Causales: La salida depende de valores presentes y pasados de la salida y la entrada. • No causales: La salida depende de valores futuros de la entrada.

Sistemas Analógicos Discretos Operadores de tiempo discreto (Equivalentes a las derivadas de la Ecuación Diferencial) El operador de tiempo discreto mas utilizado es el operador retardo z -1, z-1 x[n]=y[n]=x[n-1] Ej. y[n]=4 z 3 x [n]+6=4 x[n+3]+6

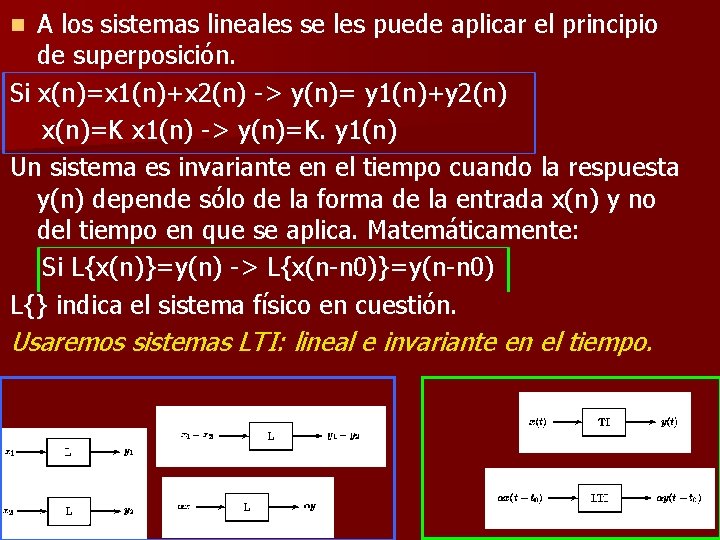
A los sistemas lineales se les puede aplicar el principio de superposición. Si x(n)=x 1(n)+x 2(n) -> y(n)= y 1(n)+y 2(n) x(n)=K x 1(n) -> y(n)=K. y 1(n) Un sistema es invariante en el tiempo cuando la respuesta y(n) depende sólo de la forma de la entrada x(n) y no del tiempo en que se aplica. Matemáticamente: Si L{x(n)}=y(n) -> L{x(n-n 0)}=y(n-n 0) L{} indica el sistema físico en cuestión. n Usaremos sistemas LTI: lineal e invariante en el tiempo.

Los filtros digitales pueden ser considerados sistemas de tiempo discreto, la expresión general es, y[n]+A 1 y[n-1]+. . . +AN y[n-N]=B 0 x[n]+B 1 x[n-1]+. . . +BM x[n-M] esta es la expresión de un filtro recursivo de orden N, el cual posee una respuesta impulsiva h[n]de longitud infinita (IIR) Si todos los coeficientes Ak son 0, se transforma en la expresión de un filtro no recursivo descritpto por, y[n]= B 0 x[n]+B 1 x[n-1]+. . . +BM x[n-M] Este filtro posee una respuesta impulsiva finita (FIR) al no existir recursividad. Respuesta impulsiva de filtros no recursivos Un filtro no recursivo de longitud M+1 se describe por, y[n]= B 0 x[n]+B 1 x[n-1]+. . . +BM x[n-M] SI x[n]= [n], la respuesta impulsiva es, h[n]= B 0 [n]+B 1 [n-1]+. . . +BM [n-M]

Estabilidad de sistemas lineales invariantes en tiempo discreto Un sistema lineal invariante en tiempo discreto es estable si las raices de su ecuación característica tienen todas modulo menor a 1 Ej. y[n]-1/6 y[n-1]-1/6 y[n-2]=x[n], Su ecuación característica es: z 2 -1/6 z-1/6 =0 Con raíces z 1=1/2, z 2=-1/3 por lo tanto el sistema es estable.

Respuesta impulsiva de Sistemas (filros digitales) ¿Porqué es importante la respuesta impulsiva de un sistema? Existen dos formas de representar un sistema físico, en el dominio de la frecuencia y en el dominio del tiempo. En el primer caso se trata de la respuesta en frecuencia, la que veremos mas adelante cuando analicemos la transformada de Fourier y en el segundo a través de la respuesta al impulso de un sistema. Si se suman infinitos términos cosenoidales cuya frecuencia varia de 0 a infinito, se obtiene una señal impulsiva, por lo tanto aplicar un impulso a la entrada de un sistema es equivalente a aplicar infinitos cosenos con un rango infinito de frecuencias, entonces el resultado que se obtiene es representativo del sistema físico bajo estudio. ¿A partir de conocer la respuesta impulsiva de un sistema puedo calcular la respuesta para cualquier entrada? Si, efectivamente. SOLUCIÓN ------ CONVOLUCIÓN

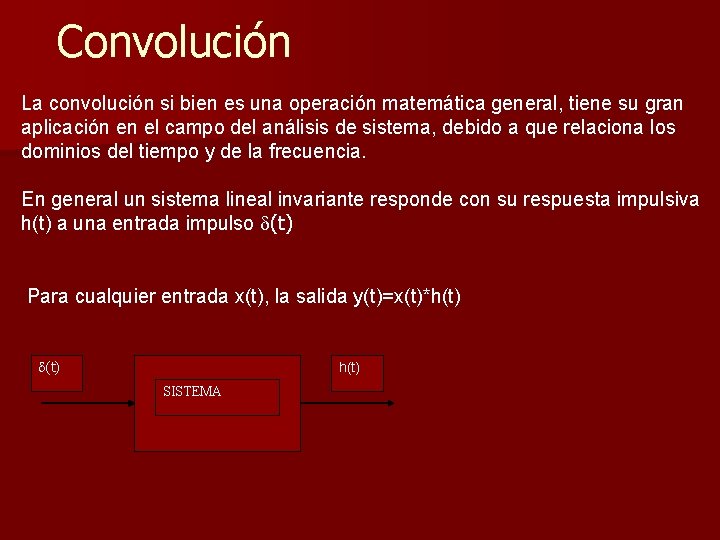
Convolución La convolución si bien es una operación matemática general, tiene su gran aplicación en el campo del análisis de sistema, debido a que relaciona los dominios del tiempo y de la frecuencia. En general un sistema lineal invariante responde con su respuesta impulsiva h(t) a una entrada impulso (t) Para cualquier entrada x(t), la salida y(t)=x(t)*h(t) h(t) SISTEMA

Convolución (Dominio continuo) Podremos calcular la respuesta y(t) de un sistema a una entrada cualquiera x(t). n Condiciones para llevarla a cabo: Sistema LTI Respuesta al impulso del sistema h(t) n Basándonos en el principio de superposición y en que el sistema es invariante en el tiempo:

Una señal arbitraria de entrada x(t) puede expresarse como un tren infinito de impulsos. Para ello, dividimos x(t) en tiras rectangulares de anchura ts y altura x(k ts). Cada tira la reemplazamos por un impulso cuya amplitud es el área de la tira : ts. x(k. ts) δ(t –Kts) n La función xs(t) que aproxima x(t) es : x(t) es el límite cuando ts -> dλ , kts->λ : Y aplicando el principio de superposición: Convolución

Respuesta impulsiva de Sistemas Discretos (Convolución Discreta) Convolución discreta x(n)*h(n)

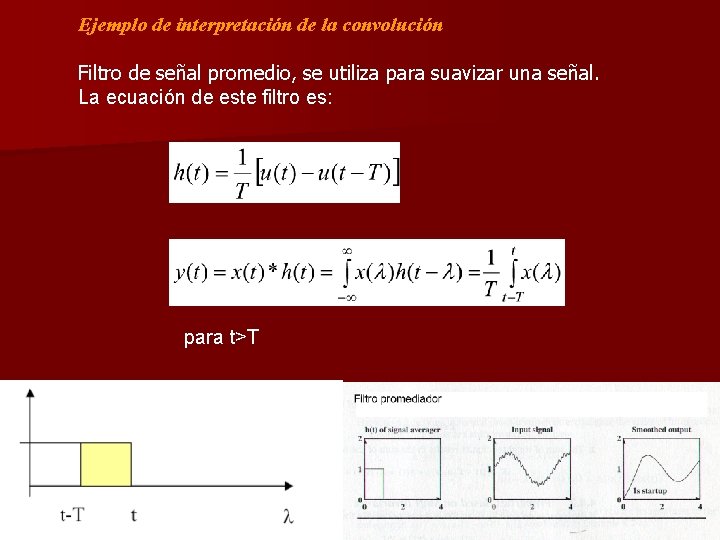
Ejemplo de interpretación de la convolución Filtro de señal promedio, se utiliza para suavizar una señal. La ecuación de este filtro es: , para t>T

Ej. Mostrar como la convolución explica el manchado (borroso) de un objeto en movimiento en una fotografía.

Convolución Discreta En este curso nosotros prestaremos especial atención a la convolución discreta la cual posee una interpretación análoga a la del caso continuo, solo que se aplica a señales de tiempo discreto, esta se define como, y[n]=x[n]*h[n]= x[k]h[n-k]

Propiedades de la convolución n Propiedades (se supone que x(t)*h(t)=y(t)):

Conclusiones para la Convolución n Mediante convolución hemos sido capaces de determinar la respuesta del sistema a una señal de entrada a partir de la respuesta del sistema a una entrada impulso. n La función h(t) se define para t>=0 La respuesta en t 0 depende de los valores actual y pasados de la entrada y de la respuesta al impulso. n n Los valores más recientes de x(t) son multiplicados por sus correspondientes más antiguos (y más grandes) valores de h(t).

Correlación La correlación es una operación similar a la convolución, la mide el grado de dependencia entre dos señales. Cuando se trabaja con una misma señal desplazada en el tiempo se denomina autocorrelación y cuando se trabaja con dos señales diferentes se denomina intercorrelación o correlación cruzada. En procesamiento de señales tiene mas aplicación la correlación cruzada la cual revela el grado de similitud entre dos señales. Al igual que la función convolución la correlación se puede definir en el campo continuo y en el campo discreto, en este curso trabajaremos con la correlación discreta. Definición: Autocorrelación: Rxx= x[k]x[k-n] = x[n]*x[-n], cuando k 0 Rxx es máxima, cuando k , Rxx es mínima. Correlación cruzada: Rxy= x[k]y[k-n] = x[n]*y[-n], n=0, 1, 2, . . . Ejemplo de uso de la autocorrelación: Radar.

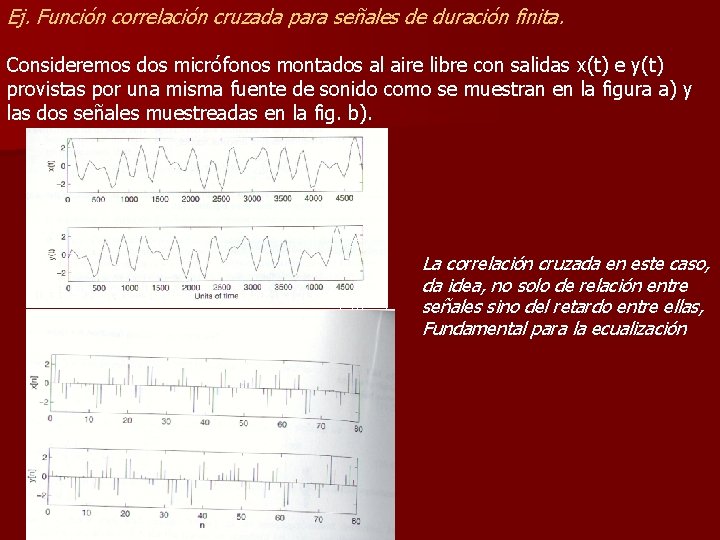
Ej. Función correlación cruzada para señales de duración finita. Consideremos dos micrófonos montados al aire libre con salidas x(t) e y(t) provistas por una misma fuente de sonido como se muestran en la figura a) y las dos señales muestreadas en la fig. b). Rxy= x[k]y[k-n] La correlación cruzada en este caso, da idea, no solo de relación entre señales sino del retardo entre ellas, Fundamental para la ecualización

Ej. Identificación de sistemas Un requerimiento común en el procesamiento de señales es caracterizar un sistema desconocido, determinando su respuesta impulsiva. De cualquier manera para obtenerla seria necesario una señal impulsiva la cual tiene amplitud infinita y ancho cero, lo cual es físicamente irrealizable. Una alternativa es aplicar un ruido al sistema y calcular la correlación cruzada entre la entrada y la salida. Consideremos una señal de ruido n(t) aplicada al sistema con respuesta impulsiva h(t), la salida y(t)=n(t)*h(t) A su vez Ryn=y(t)*n(-t)=[n(t)*h(t)]*n(-t)=Rnn(t)*h(t) Si la entrada de ruido tiene un ancho de banda muy grande (ruido blanco para el sistema considerado), la autocorrelación Rnn es un pico mucho mas angosto que la respuesta impulsiva del sistema, de esta forma Ryn(t)=h(t) Esto significa que si se aplica un ruido blanco al sistema desconocido, la respuesta impulsiva de este sistema se obtiene como la correlación cruzada de la entrada y la salida.