PRAVILA ZAKLJUCIVANJA I DOKAZI Od stare Grke do

PRAVILA ZAKLJUCIVANJA I DOKAZI • • • Od stare Grčke do danas matematičari su koristili dokaz na putu od nepoznatog do poznatog. Svaka nova generacija matematičara je gledala da unapredi postojaca znanja. Matematičari za razliku od ostalih naučnika posebno su vodili računa o jasnom definisanju pojmova i njihovom dokazivanju Poznata je anegdota iz knjge Koncepti moderne matematike od Ijana Stuarda: Astronom, fizičar i matematičar bili su na odmoru u Škotskoj. Gledajući kroz prozor voza spazili su crnu ovcu na livadi. Interesantno, primetio je astronom, sve škotske ovce su crne. Na ovo fizičar je odgovorio: ne, ne! Neke škotske ovce su crne. Matematičar je zamišljeno gledao u nebo i rekao: U Škotskoj postoji najmanje jedno polje, koje sadrži najmanje jednu ovcu, čija je najmanje jedna strana crna.

• Zašto proučavamo pravila zaključivanja? • Generalno za nauku je izuzuzetno važno pravilno zaključivati. • • A danas u računarskoj struci to je izuzetno važno. Zašto? Pa računar je mašina. Mašina radi samo ono što joj kažemo. • Zato pravila zaključivanja moraju biti jasna i nedvosmislena.

• Znači, pravila zaključivanja moraju biti jasna i nedvosmislena. • Međutim, logička zaključivanja često mogu biti pogrešna, što je posledica primene pravila ograničenog prostora dejstva. • VAŽNO • Pogrešna pretpostvaka ne može da dovede do tačnog zaljučka. • Tačna pretpostavka ne mora da dovede do tačnog zaključka.

DEDUKCIJA I INDUKCIJA • Znanja u nauci dele se na: empirijska i apriorna. • • Empiriska znanja su bazirana na iskustvu. Aprioriorna znanja se ne moraju opravdati iskustvom, ona postoje i bez iskustva. • U otkrivanju znanja, čovek se mora koristiti nekim metodama zaključivanja. • Zaključivanje je misaoni proces u kome izvodimo jedno tvrđenje na osnovu jednog ili više drugih. U suštini postoje da osnovna principa zaključivanja: to su dedukcija i indukcija. •

DEDUKTIVNA METODA • Dedukcija je princip zaključivanja od od poznatog ka nepoznatom, od opšteg ka posebnom. • Deduktivnom metodom do zaključka dolazimo na osnovu drugih ranije poznatih stavova koje zovemo predpostavke , hipoteze ili premise. • Deduktivnost znači izvodljivost. • Deduktivni zaključak oslanja se na pravila i zakonitosti matematilče logike. • Važna napomena: kod dedukcije nas u principu ne interesuje da li su predpostavke i zaključci istiniti, već nas jedino interesuje da li se iz datih predpostavki može izvesti zaključak, odnosno da li je tačan princip zaključivanja. • • • Matematika je u suštini deduktivna nauka. U deduktivne ili teorijske metode spadaju: metoda dokazivanja, metoda analize, metoda sinteze, i dr.

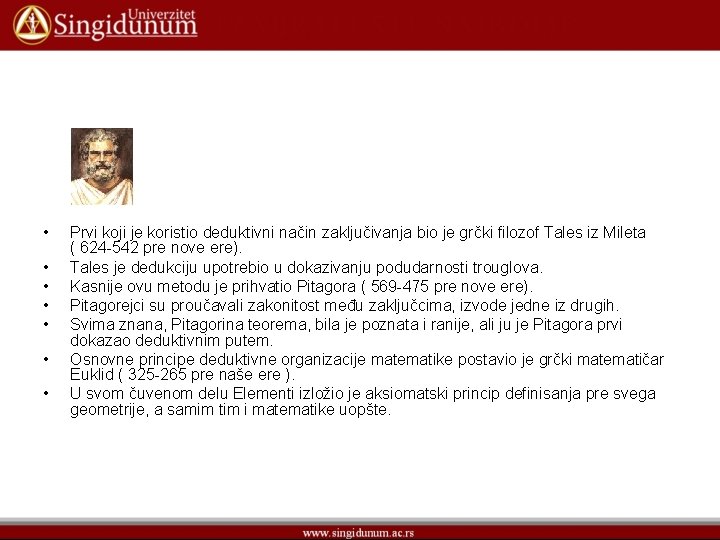
• • Prvi koji je koristio deduktivni način zaključivanja bio je grčki filozof Tales iz Mileta ( 624 -542 pre nove ere). Tales je dedukciju upotrebio u dokazivanju podudarnosti trouglova. Kasnije ovu metodu je prihvatio Pitagora ( 569 -475 pre nove ere). Pitagorejci su proučavali zakonitost među zaključcima, izvode jedne iz drugih. Svima znana, Pitagorina teorema, bila je poznata i ranije, ali ju je Pitagora prvi dokazao deduktivnim putem. Osnovne principe deduktivne organizacije matematike postavio je grčki matematičar Euklid ( 325 -265 pre naše ere ). U svom čuvenom delu Elementi izložio je aksiomatski princip definisanja pre svega geometrije, a samim tim i matematike uopšte.

INDUKTIVNA METODA • Indukcija je metod zaključivanja kojim se iz stavova koji se odnose na određen broj pojedinačnih slučajeva izvodi stav koji se odnosi na sve slučajeve te vrste. • Ovaj metod zaključivanja često se koristi u prirodnim naukama, gde se posmatranjem ili eksperimentom dolazi do određenih saznanja o nekoj pojavi, pa se na osnovu ovih pojedinačnih slučajeva izvodi opšti stav. • Takva indukcija se naziva nepotpuna ili empirijska indukcija. Ovakav način zaključivanja nije dobar, jer se često na osnovu određenog broja tačnih pojedinačnih slučajeva ne dobija tačan zaključak u oštem slučaju. • Primer: Fermaov problem: Da li su prosti brojevi oblika ? Zamenom za n=1, 2, 3, 4 dobijaju se prosti brojevi. To bi moglo da dovede do zaključka da su brojevi zaista prosti. Međutim za n=5, dobija se broj deljiv sa 641, znači broj koji nije prost.

• • • U induktivne ili empiriske metode spadaju: metoda eksperimenta, metoda posmatranja, metoda merenja, metoda analogije i dr. • • Napomena: Dedukciju i indukciju je u praksi često teško razdvojiti, ali to su dve različite metode i koje se u suštini međusobno isključuju. • Ako bi ih upoređivali, možemo reći da dedukcija vodi za nužnim zaključcima, dok indukcija ka verovatnim zaključcima. • Deduktivne metode se bave isključivanjem pogrešnih pretpostavki, ali ne i utvrđivanjem istinitosti • Induktivne metode se bave utvrđivanjem činjenične istinitosti.

MATEMATIČKI DOKAZ • • Matematički dokaz je mnogo strožiji od dokaza koji se koristi u drugim naukama ili svakodnevnom životu. Matematički dokazi su apsolutni. Što se jednom dokaže to je zauvek tačno. • • Matematički dokaz počinje uvođenjem 1. Osnovnih pojmova 2. Aksioma ( za koje se pretpostavlja da su istinite ) 3. Definicija 3. Koristeći logičke argumente, korak po korak, dolazi se do zaključka. 4. Ako su aksiome tačne i logika ispravna, zaključak mora biti tačan. 5. Taj zaključak je teorema.

DOKAZ MATEMATIČKIH POJMOVA definicije, aksiome i dokazi • • U matematici postoje pojmovi koji se ne definišu. Oni se shvataju uz pomoć intuicije, iskustva ili dogovora. Njih nazivamo osnovnim ili primitivnim pojmovima. • Naprimer, tačka, skup ili prirodni broj 1 su osnovni pojmovi. Svima su ti pojmovi intuitivno jasni i svaki pokušaj njihovog definisanja kroz istoriju matematike nisu doveli do rezultata. Veliki matematičar Euklid u svome delu Elementi dao je definiciju tačke. Rekao je „ Tačka je ono čiji je deo ništa “. Naravno ovo je nepotrebna definicija, koja je nasmejala ne samo matematičare i koja je vremenom nestala. • Svi ostali novi pojmovi se moraju definisati, koristeći samo osnovne pojmove ili one koje smo već definisali. Definicije služe da bi se pojmovi precizno odredili. Definicija je iskaz ili sud kojim se nedvosmismeno određuje sadržaj pojma. • • Primer: Definicija: Za svake dve prave a i b kažemo da se seku ako imaju tačno jednu zajedničku tačku. Definicija: Dve prave su paralelne, ako leže u istoj ravni i nemaju zajedničkih tačaka ili se poklapaju.

• Definicije su često oblika: • ekvivalencije, A ako i samo ako B, u oznaci , • jednakosti, A jednako B, u oznaci Primer:

• • • Postoje i tvrđenja koja nije potrebno dokazivati. To su aksiome. Pomoću njih izgrađuju se matematičke teorije. Aksiome ili postulati su tvrđenja koja se ne dokazuju, koja su sama po sebi uvek istinita. Prvi sistem aksioma definisao je Euklid u 3 v. p. e. Primer: Aksioma: Za bilo koje dve različite tačke postoji tačno jedna prava koja ih sadrži. Aksioma: Za svaku pravu p i tačku A van nje, postoji tačno jedna prava koja sadrži tačku A i paralelna je pravoj p. Druga navedena aksioma je poznata aksioma paralelnosti. Nju je definisao još Euklid i poznata je pod imenom 5 postulat. Vekovima su matematičari pokušavali da je dokažu, sve dok u prvoj polovini 19. veka matematičar Lobačevski nije dokazao da je to aksioma koja je neophodna skupu aksioma euklidske geometrije. Lobačevski i Gaus su postavili pitanje koja od ovih geometrija predstavlja stvarnu sliku sveta, obavili su i par eksperimenata, ali pitanje je ostalo bez odgovora. Aksiome treba izabrati da nisu protivrečne i da ih ima dovoljno za dokazivanje teorema.

• • • Posledice aksiome su teoreme. Svaka teorema sastoji se od pretpostavke – hipoteze i zaključka –posledice. Sve teoreme (tvrđenja, stavove) moramo dokazati. • • Logičko rasuđivanje pomoću koga dolazimo do zaključaka je dokaz. Dokaz se sastoji od niza koraka i sadrži: a) Definicije, aksiome i već dokazane teoreme b) Pravila izvođenja i logičke zakone zaključivanja. • • • Svaka terema ima bar 1 dokaz. Dokazi mogu biti direktni i indirektni: Da iz uslova A, B, C, …. sledi posledica F i koristimo se simbolikom u pisanju • Dokaz prestavlja zaštitni znak matematike. Pravilna upotreba dokaza je od suštinskog značaja za matematiku.

PRAVILA ZAKLJUČIVANJA MODUS PONENS • • • Modus ponens je najčešće primenjivano, a ujedno i najjednostavnije pravilo dokazivanja. Naziv je latinski i u prevodu znači metod potvrđivanja. Ovo je primer direktnog dokaza • • Može da se čita, ako iz A i A sledi B, onda B. Ovo pravilo zaključivanja opravdava tautologija • • Primer: A : Napolju pada kiša. Ako napolju pada kiša, poneću kišobran. B: Poneću košobran • • Primer: A: 2000 je deljivo da 5, Ako je N deljivo sa 5, onda je N prestupna godina. B: 2000 je prestupna godina.

MODUS TOLENS Ovo je takođe primer direktnog dokaza • Naziv je takođe latinski i znači metoda opovrgavanja. • Ovo pravilo zaključivanja opravdava tautologija • • Primer: Ako izvršim zločin, biću uhapšen. • : Nisam izvršio zločin

PRAVILO KONTRADIKCIJE •

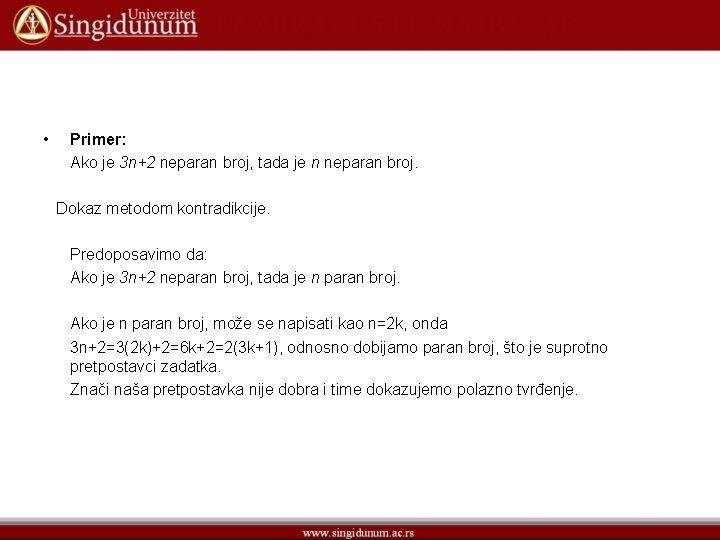
• Primer: Ako je 3 n+2 neparan broj, tada je n neparan broj. Dokaz metodom kontradikcije. Predoposavimo da: Ako je 3 n+2 neparan broj, tada je n paran broj. Ako je n paran broj, može se napisati kao n=2 k, onda 3 n+2=3(2 k)+2=6 k+2=2(3 k+1), odnosno dobijamo paran broj, što je suprotno pretpostavci zadatka. Znači naša pretpostavka nije dobra i time dokazujemo polazno tvrđenje.

PRAVILO KONTRADIKCIJE •

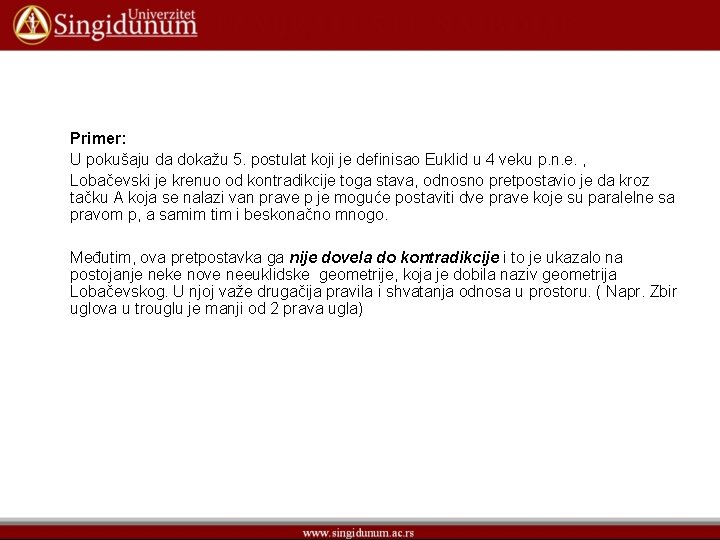
Primer: U pokušaju da dokažu 5. postulat koji je definisao Euklid u 4 veku p. n. e. , Lobačevski je krenuo od kontradikcije toga stava, odnosno pretpostavio je da kroz tačku A koja se nalazi van prave p je moguće postaviti dve prave koje su paralelne sa pravom p, a samim tim i beskonačno mnogo. Međutim, ova pretpostavka ga nije dovela do kontradikcije i to je ukazalo na postojanje neke nove neeuklidske geometrije, koja je dobila naziv geometrija Lobačevskog. U njoj važe drugačija pravila i shvatanja odnosa u prostoru. ( Napr. Zbir uglova u trouglu je manji od 2 prava ugla)

PRAVILO KONTRAPOZICIJE • Dokaz kontrapozicijom • Ovo pravilo zaključivanja opravdava tautologija • Primer: Potrebno je biti jak da bi bio bokser, • kontrapozicija glasi: Ako nisi bokser nije potrebno biti jak.

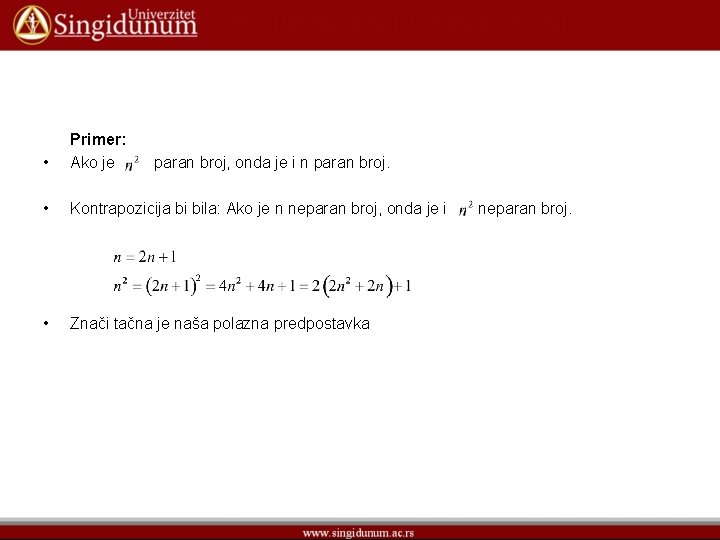
• Primer: Ispitati da li je funkcija • Ako je ispunjeno • Izrazi koji u sebi sadrže nejednakosti se teško dokazuju i jednostavnije je koristiti kontrapoziciju predhodnog izraza koja glasi. preslikavanje Dakle , čime smo dokazali da je preslikavanje “ 1 -1”. 1 -1. preslikavanje je “ 1 -1”.

• Primer: Ako je • Kontrapozicija bi bila: Ako je n neparan broj, onda je i • Znači tačna je naša polazna predpostavka paran broj, onda je i n paran broj. neparan broj.

PRAVILO TRANZITIVNOSTI IMPLIKACIJE I EKVIVALENCIJE • Pravilo tranzitivnosti za implikaciju ( pravilo silogizma) i ekvivalenciju: • Ova pravila zaključivanja opravdavaju tautologije • • • Primer: Ako je čovek umetnik, onda je on je srećan. Ako je čovek srećan, onda on dugo živi. Zaključak Umetnici dugo žive. Primer: Ako je broj deljiv sa 18 onda je deljiv sa 6. Ako je broj deljiv sa 6 onda je deljiv sa 3. Ako je broj deljiv sa 18 onda je deljiv sa 3. • • •

DOKAZ KONTRAPRIMEROM • • Dovoljno je da nađemo neku vrednost promenljive x za koje tvrđenje nije tačno, da oborimo tačnost polaznog tvrđenja. Primer: Proizvod svaka dva iracionalna broja je iracionalan. Kontraprimer: ako su dati iracionalni brojevi je racionalan broj. i , njihov proizvod

• Generalizacija – uopštavanje • Specijalizacija • • Kod ove vrste zaključivanja postoji višak informacija, nepotrebne se odbacuje , a pažnja se usmerava samo ka željenom svojstvu. Primer: Želimo da odredimo da li je student položio matematiku, koja je ispit prve godine. Utvrđujemo da je student položio sve predmete prve godine. Znači, student je položio matematiku. • Eliminacija • Kada imamo dve mogućnosti, a jednu od njih isključimo, druga mora da važi. Primer: Naći sva pozitivna rešenja jednačine Rešavanjem jednačine dobijaju se dva rešenja , ali poto tražimo samo pozitivna rešenja uzimamo samo x=1. • •

PRAVILA ZAKLJUČIVANJA Modus ponens • Modus tolens • Kontrapozicija • • Generalizacija-uopštavanje • • • Kontradikcija –protivrečnost Eliminacija-disjunktivni silogizam Specijalizacija -simplifikacija Tranzitivnost implikacije-silogizam Tranzitivnost ekvivalencije

Greške zaključivanja • Često se pojavljuju greške zaključivanja: 1. Ispravnost zaključka nije uslovljena istinitišću predpostavki. Slatkiši su dobri za liniju Čokolada je slatkiš Čokolada je dobra za liniju

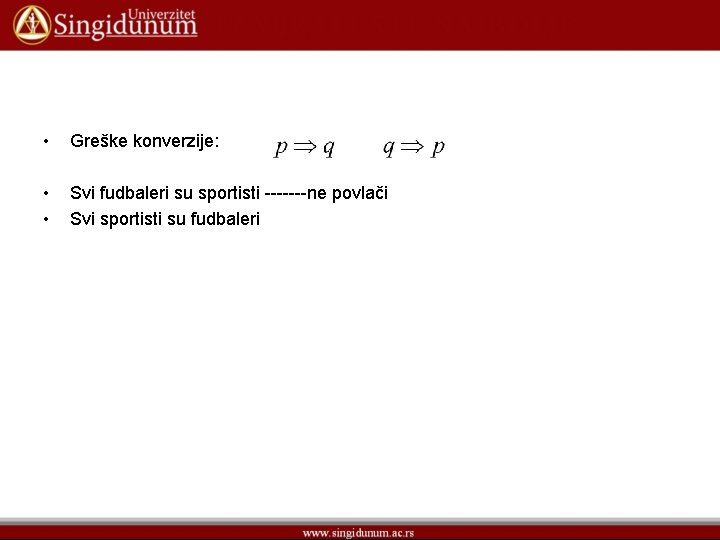
• Greške konverzije: • • Svi fudbaleri su sportisti -------ne povlači Svi sportisti su fudbaleri

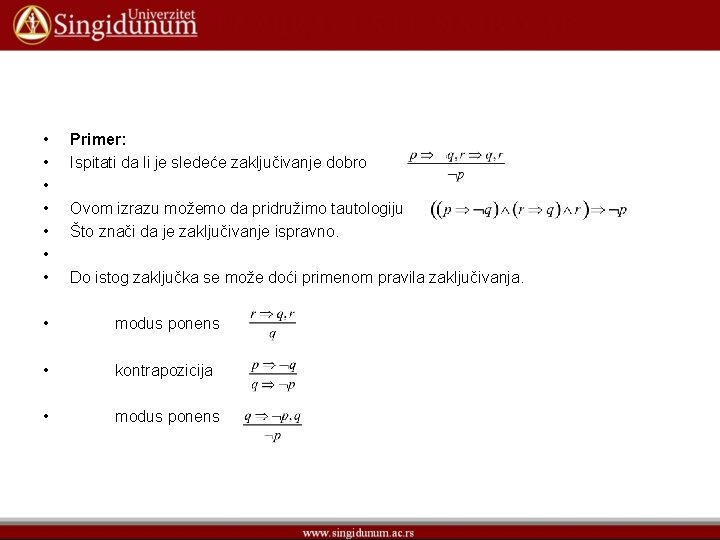
• Primer: Ispitati da li je sledeće zaključivanje dobro • Ovom izrazu možemo da pridruzimo iskaznu formulu p q T T T • T T Iz tablice za ispitivanje istinitosti vidi se da u četvrtom redu iz tačnih predpostavki ne dobija se tačan zaključak.

• • Primer: Ispitati da li je sledeće zaključivanje dobro Ovom izrazu možemo da pridružimo tautologiju Što znači da je zaključivanje ispravno. Do istog zaključka se može doći primenom pravila zaključivanja. • modus ponens • kontrapozicija • modus ponens

MATEMATIČKA INDUKCIJA • • Matematika je više deduktivna nauka, tj. metod zaključivanja je od opšteg ka posebnom. Međutim, mnoge matematičke probleme moguće je proučavati induktivnom metodom, odnosno istraživački, stvaralački postupak po pravilu je induktivan. • Princip matematičke indukcije isključuje mogućnost greške, koja može da se pojavi u empirijskoj indukciji, jer se odnosi na sve moguće slučajeve. • • • Neka je T(n) teorema, tvrđenje, čija formulacija sadrži prirodni broj. Ako je teorema tačna za n=1 , pod pretpostavkom da je tačna za bilo koji prirodni broj n=k , ako dokažemo da važi za n=k+1, onda je teorema tačna za sve prirodne brojeve.

• • Primer: Dokazati da važi jednakost 1. Za n=1 imamo jednakost je tačna. • 2. Za n=k imamo tačna. . Pretpostavljamo da je jednakost • 3. Za n=k+1 je . Treba da dokažemo, pod • pretpostavkom 2, da je jednakost 3 tačna. Ako obema strana jednakosti dodamo sabirak dobijamo čime smo dokazali da je pod pretpostavkom 2, jednakost tačna i za n=k+1 , odakle zaključujemo da je formula tačna za sve prirodne brojeve.

• • Primer: Dokazati da je izraz deljiv sa 5 1. Za n=1 imamo , 6 -5+4=5, izraz je deljiv sa 5. 2. Za n=k imamo , pretpostavljamo da je izraz deljiv sa 5. 3. Za n=k+1 je Treba da ispitamo deljivost sa 5 , pod pretpostavkom 2. Kako je svaki sabirak deljiv sa 5, proizilazi i da je ceo zbir deljiv sa 5, odakle zaključujemo da je formula tačna za sve prirodne brojeve.

Temelji znanja ? ? ? • • • ALI krajem 19 veka matematičari su počeli da se vraćaju unazad. Želeli su da provere temelje matematike. Tim problemom su se najviše bavili logičari. • • • Primer: Zakon trihotomije: Svaki broj je pozitivan, negativan ili nula. Ovo deluje očigledno i vekovima su matematičari ovo prećutno prihvatali kao istinu. Ali logičari su želeli strogi dokaz, jer ako je neistinit sva znanja koja se baziraju na ovom zakonu padaju. •

• Čuveni matematičar Hilbert predvodio je program kojim bi se dokazalo da je • • 1. Matematika kompletna- mogla bi da odgovori na sva moguća pitanja 2. Matematika je nekonzistentna –odnosno ako neto tvrđenje dokažemo pomoću jedne metode, ne bi nekom drugom metodom mogli da dokažemo da je neistinita. Bio je ubeđen da pomoću dovoljnog broja aksioma možemo da rešimo postavljeni problem. •

• • • Mnogi matematičari su krenuli da reše postavljeni problem, i malo pre nego što bi 1902 matematičar Frege izdao dokaz ( knjiga mu je bila u štampi) Rasel definiše svoj paradoks –o kome je već bilo reči u teoriji skupova 1931 g Gedel zauvek uništava Hilbertove nade. Dokazao je da matematika nije logički savršena i da postoje problemi koji mogu biti nerešeni. 1963 Koen je razvio tehniku za dokazivanje neodlučivosti.

• ALI- Mašinsko učenje • Mašinsko učenje je podoblast vještačke inteligencije čiji je cilj konstruisanje algoritama i računarskih sistema koji su sposobni da: • • • Automatizuju programiranje Samoprogramiraju Neka sami podaci „rade posao“ umesto klasičnog programiranja

ZAŠTO MAŠINSKO UČENJE ? • • Mašinsko učenje je u užem smislu programiranje računarskih mašina u cilju optimizacije pogodnog kriterijuma optimalnosti, na osnovu raspoloživih podataka ili prošlih iskustava. • Učenje je neophodno kada: • –Ne postoje eksperti za datu oblast (navigacija na Marsu) • –Ljudi nisu u stanju da objasne svoju ekspertizu (prepoznavanje govora, prepoznavanje znakova) • –Rešenje se menja u vremenu (rutiranje u računarskim mrežama) • –Rešenje je neophodno prilagoditi konkretnim situacijama i slučajevima (biometrija)