PHYSIQUECHIMIE E T MATHMATIQUES Vers un nouveau lyce

PHYSIQUE-CHIMIE E T MATHÉMATIQUES Vers un nouveau lycée Année scolaire 2018 -2019 Sources : Groupes mathématique et physique-chimie de l’Inspection Générale Séminaire « Croisements didactiques : mathématiques et physique-chimie » du 10 mars 2017 Groupe Maths-Physique et Chimie de l’IREM de Paris Université Paris Diderot Pierre Rigat IA-IPR Physique-chimie

Les programmes de mathématiques et de physiquechimie : Des liens affichés et des points de rencontres explicites à mettre en place 6 compétences sont travaillées au collège et au lycée, …. . proches de celles de la démarche scientifique • CHER, expérimenter – en particulier à l’aide d’outils logiciels ; • MODÉLISER, faire une simulation, valider ou invalider un modèle ; • REPRÉSENTER, choisir un cadre (numérique, algébrique, géométrique. . . ), changer de registre ; • RAISONNER, démontrer, trouver des résultats partiels et les mettre en perspective ; • CALCULER, appliquer des techniques et mettre en œuvre des algorithmes ; • COMMUNIQUER un résultat par oral ou par écrit, expliquer une démarche.

Exemple du programmes de seconde, apparition de capacités mathématiques explicites • Représenter l’histogramme associé à une série de mesures à l’aide d’un tableur • Utiliser les pourcentages et les fractions. • Utiliser une grandeur quotient pour déterminer le numérateur ou le dénominateur. Effectuer le quotient de deux grandeurs pour les comparer. • Utiliser les opérations sur les puissances de 10. Exprimer les valeurs des grandeurs en écriture scientifique. • Identifier et utiliser la proportionnalité • Représenter des vecteurs. • Utiliser des grandeurs algébriques. • Identifier une fonction périodique et déterminer sa période. • Utiliser le théorème de Thalès.

Certains élèves maîtrisent mal, voire très mal, certaines de ces capacités et cela constitue un frein pour l'acquisition du programme de Physique-Chimie. r une Coefficient de proportionnalité Conversion d’unité Calcul lit me è i r t a Qu nelle n o i t r Produit en croix propo Nombre s décima ux Proportionnalité téral re Ecritu ue ifiq scient « Règle de trois » Passag e à l’unit é Ordre de grandeur lise é d o M r une a p n io situat tion de situa nnalité rtio propo Grandeur quo tient que i r é m nu Calcul Isolement d’un terme Fractions Ecriture des unit és des gran deurs da ns les calcu ls Puissance de 1 Pour lever ce frein, comment les aider à construire et renforcer durablement ces notions grâce à des liens entre les enseignements de Mathématiques de Physique-Chimie ? 0

Ressources : https: //www. pedagogie. ac-aix-marseille. fr/jcms/c_51569/fr/accueil • Guide pratique sur la proportionnalité, le calcul avec unités de grandeurs et l’isolement de terme https: //www. pedagogie. ac-aix-marseille. fr/jcms/c_10583515/fr/guide-pratique-sur-la-proportionnalite-lecalcul-avec-unites-de-grandeurs-et-lisolement-de-terme • Expérimentation et modélisation, la place du langage mathématique en physique-chimie GRIESP http: //eduscol. education. fr/fileadmin/user_upload/Physique-chimie/PDF/experimentation-modelisationplace-langage-mathematique-physique-chimie. pdf • Évolution de l'enseignement de la physique et de la chimie http: //eduscol. education. fr/physique-chimie/se-former/regard-sur-lenseignement-de-physiquechimie/evolution-de-lenseignement-de-la-physique-et-de-la-chimie. html

Merci pour votre attention !

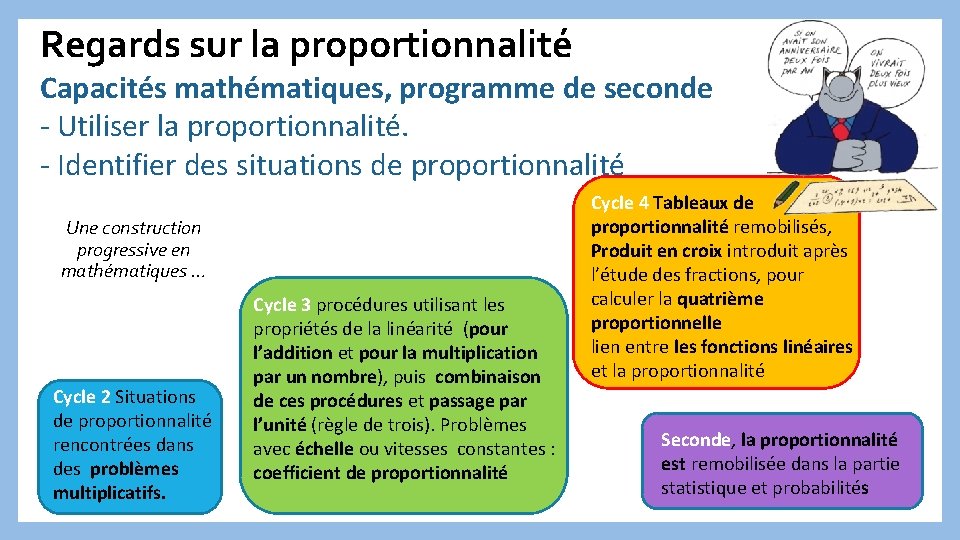
Regards sur la proportionnalité Capacités mathématiques, programme de seconde - Utiliser la proportionnalité. - Identifier des situations de proportionnalité Une construction progressive en mathématiques … Cycle 2 Situations de proportionnalité rencontrées dans des problèmes multiplicatifs. Cycle 3 procédures utilisant les propriétés de la linéarité (pour l’addition et pour la multiplication par un nombre), puis combinaison de ces procédures et passage par l’unité (règle de trois). Problèmes avec échelle ou vitesses constantes : coefficient de proportionnalité Cycle 4 Tableaux de proportionnalité remobilisés, Produit en croix introduit après l’étude des fractions, pour calculer la quatrième proportionnelle lien entre les fonctions linéaires et la proportionnalité Seconde, la proportionnalité est remobilisée dans la partie statistique et probabilités

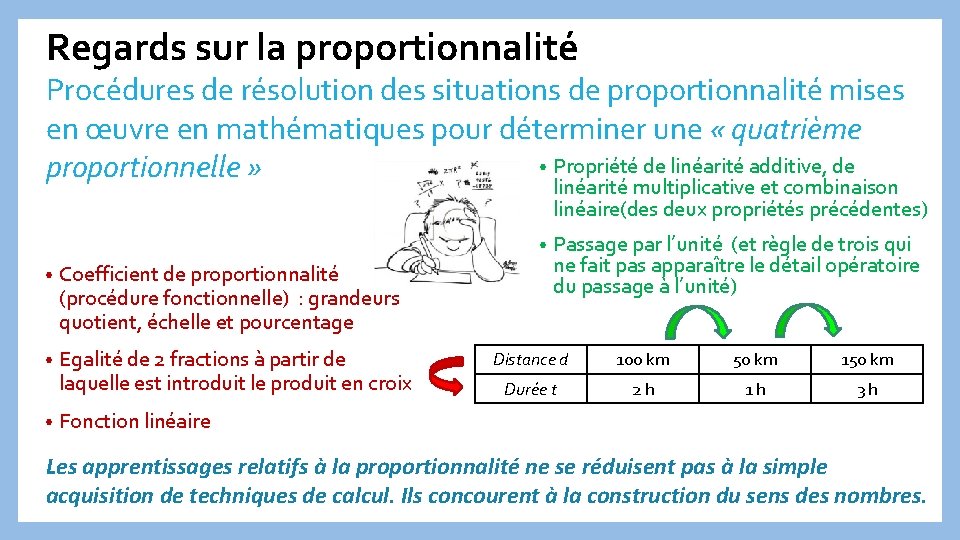
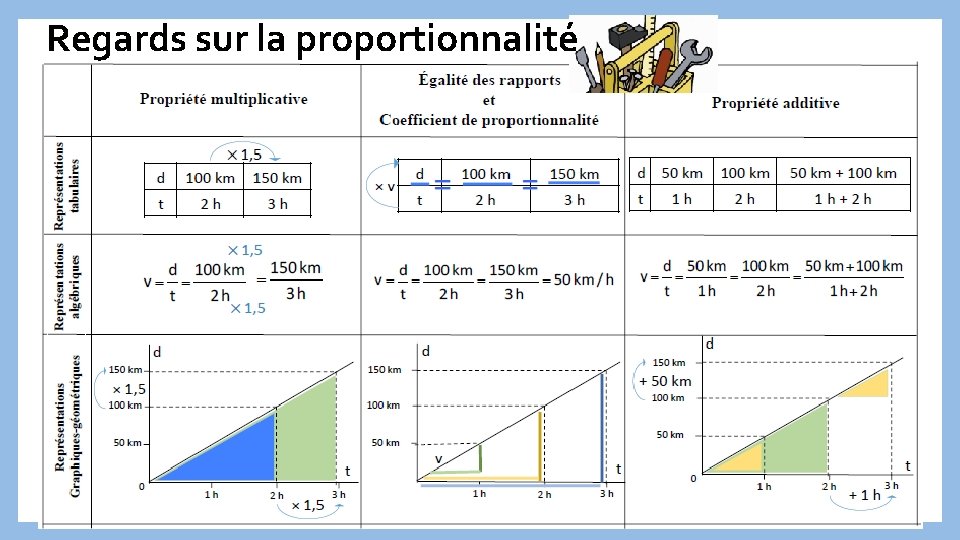
Regards sur la proportionnalité Procédures de résolution des situations de proportionnalité mises en œuvre en mathématiques pour déterminer une « quatrième • Propriété de linéarité additive, de proportionnelle » linéarité multiplicative et combinaison linéaire(des deux propriétés précédentes) • • Coefficient de proportionnalité (procédure fonctionnelle) : grandeurs quotient, échelle et pourcentage • Egalité de 2 fractions à partir de laquelle est introduit le produit en croix • Passage par l’unité (et règle de trois qui ne fait pas apparaître le détail opératoire du passage à l’unité) Distance d 100 km 50 km 150 km Durée t 2 h 1 h 3 h Fonction linéaire Les apprentissages relatifs à la proportionnalité ne se réduisent pas à la simple acquisition de techniques de calcul. Ils concourent à la construction du sens des nombres.

Regards sur la proportionnalité

Regards sur la proportionnalité Expliciter et donner du sens par l’utilisation du langage naturel Expliciter le passage à l’unité et le coefficient de proportionnalité

Regards sur la proportionnalité CYCLE 4 : COEFFICIENT DE PROPORTIONNALITE Dans l’univers des grandeurs, le coefficient de proportionnalité est une nouvelle grandeur : une grandeur-quotient, contrairement au coefficient d’homogénéité (échelle, pourcentage) Sur une carte routière, 2 cm représentent 5 km Si 6 stylos coûtent 12 €, combien coûtent 9 stylos ? Nombre de stylos 6 9 Prix (en euros) 12 ? dans cet exemple, le coefficient est le prix à l’unité (le prix d’un stylo) 12 euros / 6 stylos = 2 euros/stylo sur le terrain. Sur cette carte, la distance entre deux villes est de 7 cm. Quelle est la distance réelle entre ces deux villes ? Distance sur la carte (cm) 2 7 Distance sur le terrain(cm) 500000 ? X 250000 Le coefficient de proportionnalité est ici un coefficient d’homogénéité Ces problèmes ne nécessitent pas forcément le passage par un coefficient de proportionnalité car il n’y a pas de série de mesures ; il peut être abordé par la quatrième proportionnelle.

Regards sur la proportionnalité CYCLE 4 : REGLE DE TROIS PASSAGE A L’UNITÉ Si 6 stylos coûtent 12 €, combien coûtent 9 stylos ? Nombre de stylosylo 6 99 Prix (en euros) 12 ? e n u s a p t s e ’ ! e u Ce n q i n h c e t e l p m i s La règle de trois ou règle de proportionnalité est une méthode mathématique permettant de déterminer une quatrième proportionnelle. Grandeur recherchée (prix de 9 stylos) notée P Il convient de privilégier le raisonnement avec passage par l’unité que les élèves peuvent formuler en début d’apprentissage oralement ou par écrit : 6 stylos valent 12 euros 1 stylo vaut « 6 fois moins » donc 12/6 (on divise le prix de 6 stylos par 6) 9 stylos valent « 9 fois plus » : P = 9 x 12/6 (on multiplie le prix d’un stylo par 9)

Regards sur la proportionnalité CYCLE 4 : PRODUIT EN CROIX Si 6 stylos coûtent 12 €, combien coûtent 9 stylos ? Nombre de stylos 6 99 Prix (en euros) 12 ? Ainsi la détermination d’une quatrième proportionnelle peut être associée à l’égalité de deux fractions et donc, elle peut être mise en relation avec le produit en croix par cet intermédiaire ? Grandeur recherchée (prix de 9 stylos) notée P Cette procédure intervient seulement après l’étude des fractions : 12 P ----- = ------- ( égal au coefficient de proportionnalité) que l’on peut transformer en 6 9 12 x 9 Px 9 12 x 9 = P x 6 ou ----- = ---- ou P = ------6 9 6 e n u s a p t s e ’ ! e u Ce n q i n h c e t e l p m i s

Regards sur la proportionnalité Mais attention à la rigueur dans l’usage du vocabulaire En mathématiques, des données rendent compte d’une situation de proportionnalité si les points du graphique sont parfaitement alignés, alors qu’en sciences expérimentales, il suffit qu’ils soient quasiment alignés.

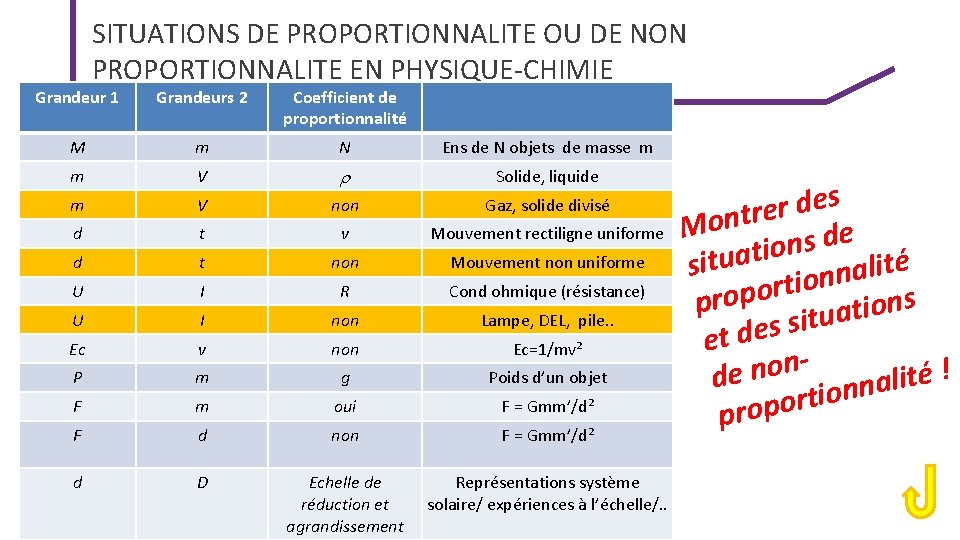
SITUATIONS DE PROPORTIONNALITE OU DE NON PROPORTIONNALITE EN PHYSIQUE-CHIMIE Grandeur 1 Grandeurs 2 Coefficient de proportionnalité M m N Ens de N objets de masse m V r Solide, liquide m V non Gaz, solide divisé d t v Mouvement rectiligne uniforme d t non Mouvement non uniforme U I R Cond ohmique (résistance) U I non Lampe, DEL, pile. . Ec v non Ec=1/mv² P m g Poids d’un objet F m oui F = Gmm’/d² F d non F = Gmm’/d² d D Echelle de réduction et agrandissement Représentations système solaire/ expériences à l’échelle/. . m - s e d r e r t n o M e d s n o i situat onnalité i t r o p o s n pr o i t a u t i s s et de n o ! n é t de i l a n n o i t r o p o r p

Regards sur le calcul littéral Quelques sources de difficultés … Le vocabulaire différent entre les disciplines sur un objet commun : formule, expression littérale, relation entre grandeurs, identité, équation, inconnue, variable, paramètre, indéterminée … • Les différentes significations d’une lettre : une constante, une grandeur inconnue, une grandeur physico-chimique… • Les différents statuts du signe « égal » : identité, égalité, équation, affectation d’une valeur en programmation …. • Les différences de présentation des relations entre les grandeurs En mathématiques, la dépendance d’une grandeur par rapport à une autre se traduit dans la notation fonctionnelle : d = f(t) avec f(t) = v t (uniquement si v constante) En physique on écrit d = v t tout le temps • Les différentes registres : langage courant, langage symbolique, tableaux de valeurs, représentations graphiques • La mise en équation du problème, les technique de résolution. •

Regards sur le calcul littéral Quelques pistes pour améliorer les apprentissages … • Donner du sens aux expressions littérales en activant les différents registres : verbal, graphique, symbolique • S’être constitué des images mentales : cercle trigonométrique et angles remarquables, courbes usuelles, … • Développer des automatismes de calcul (développement, factorisation) • Utiliser le calcul littéral pour effectuer des conversions à partir de la connaissance des préfixes de nano à giga, en laissant les unités dans les expressions Exemple : 1 m 3 = (1 m)3 = (102 cm)3 = (102)3 (cm)3 = 106 cm 3

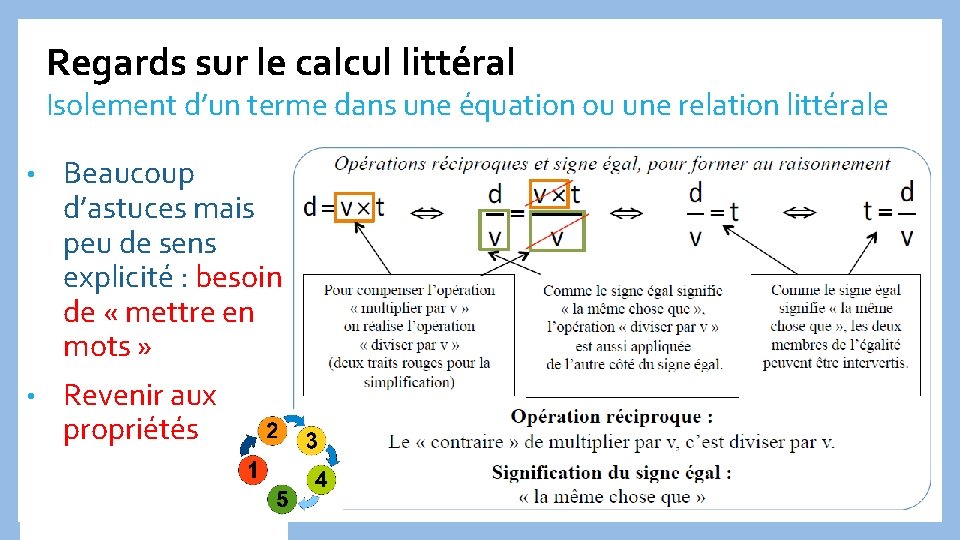
Regards sur le calcul littéral Isolement d’un terme dans une équation ou une relation littérale • Beaucoup d’astuces mais peu de sens explicité : besoin de « mettre en mots » • Revenir aux propriétés

Regards sur le calcul littéral Isolement d’un terme dans une équation ou une relation littérale • Eviter les moyens mnémotechniques (produits en croix, triangle magique, etc) qui ne font pas sens. • S’appuyer sur les connaissances du calcul numérique pour traiter des formules littérales : - L’analogie 2 -3 -6 - La résolution à partir de la substitution des grandeurs connues par leurs valeurs. U = R x I soit 10 = 50 x I et 10/50 = I soit I = 0, 20 A

Regards sur le calcul numérique A-t-on le droit de d’écrire les unités dans les calculs ? n « Mener des calculs impliquant des grandeurs mesurables, o i t a s li a n é p u o r i notamment des grandeurs en conservant les unités. » Pas de composées, o v e d n u ’ d s r lo Cycle 4 (Collège), ! Mathématiques, Grandeurs et Mesures. Extrait du programmes 2016, n e m a x e n ’u d « Il est mathématiquement légitime et pertinent pour la formation des élèves d’écrire les unités de grandeurs dans les calculs » Déclaration conjointe des groupes mathématique et physique-chimie de l’Inspection Générale, lors du Séminaire National de Formation Croisements didactiques : mathématiques et physique-chimie au collège, du 10 mars 2017 à Paris.

Regards sur le calcul numérique A-t-on le droit de d’écrire les unités dans les calculs ? Pour donner du sens aux grandeurs par une analyse dimensionnelle intégrée au calcul, faciliter les conversions et donner aux élèves une méthodologie pour identifier et comprendre leurs erreurs.

Regards sur le calcul numérique Les fractions : les obstacles Conception d’une fraction (nombre rationnel et notion de quotient), nombres décimaux, représentations (écriture fractionnaire, approximations décimales, pourcentage). Les fractions : Démarches susceptibles d’améliorer les apprentissages La verbalisation rigoureuse : 2, 3 en est une valeur décimale approché au dixième. 2, 33 au centième, 2, 333 au millième, etc. L’automatisation de certains «faits numériques » : 25 % = 1/4 ; une augmentation de 10% correspond à multiplier la quantité initiale par 1, 10 ; … L’entraînement au calcul mental et le recours raisonné (et non systématique) à la calculatrice La systématisation de procédures de contrôle des calculs ordres de grandeurs, comparaison par rapport à 1, signe

Regards sur le calcul numérique Les nombres décimaux : les obstacles • Obstacles liés à la présentation d’un nombre décimal comme étant un nombre à virgule (et les entiers ? Et 0, 3333333…. . ? ) En mathématiques : 1, 2 = 1, 200 = etc. Alors qu’en physique le nombre de chiffres significatifs dépend de la précision des mesures ou des données. En physique, 1/3 peut donc valoir 0, 3 ou 0, 333 alors que ce n’est pas un nombre décimal ! Il faut parler de valeur décimale approchée au dixième, au centième…

Regards sur le calcul numérique Les puissances de 10 : les obstacles Absence de sens attribué aux puissances de 10 (positives ou négatives) Manque de maitrise technique dans leur utilisation pour simplifier des produits ou des quotients Les puissances : Démarches susceptibles d’améliorer les apprentissages En cas de difficulté, un retour à la définition plutôt qu’une application de « règles » Un entraînement régulier au calcul (questions flash sous différentes modalités ) Un usage réfléchi et non systématique de la calculatrice Une utilisation de contextes et d’outils variés : • Masse, distances, tailles • Graphe unidimensionnel dont l’axe est gradué en fonction de l’exposant de la puissance de 10 pour classer des objets selon leur ordre de grandeur. • Conversions d’unités de masse et de distance mais jamais hors contexte

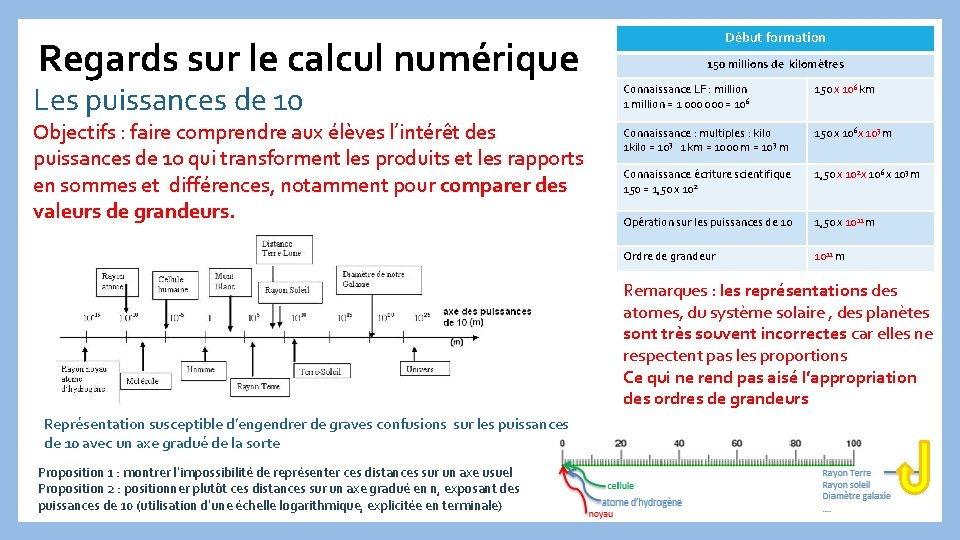
Regards sur le calcul numérique Les puissances de 10 Objectifs : faire comprendre aux élèves l’intérêt des puissances de 10 qui transforment les produits et les rapports en sommes et différences, notamment pour comparer des valeurs de grandeurs. Début formation 150 millions de kilomètres Connaissance LF : million 1 million = 1 000 = 106 150 x 106 km Connaissance : multiples : kilo 1 kilo = 103 1 km = 1000 m = 103 m 150 x 106 x 103 m Connaissance écriture scientifique 150 = 1, 50 x 102 x 106 x 103 m Opération sur les puissances de 10 1, 50 x 1011 m Ordre de grandeur 1011 m Remarques : les représentations des atomes, du système solaire , des planètes sont très souvent incorrectes car elles ne respectent pas les proportions Ce qui ne rend pas aisé l’appropriation des ordres de grandeurs Représentation susceptible d’engendrer de graves confusions sur les puissances de 10 avec un axe gradué de la sorte Proposition 1 : montrer l’impossibilité de représenter ces distances sur un axe usuel Proposition 2 : positionner plutôt ces distances sur un axe gradué en n, exposant des puissances de 10 (utilisation d’une échelle logarithmique, explicitée en terminale)

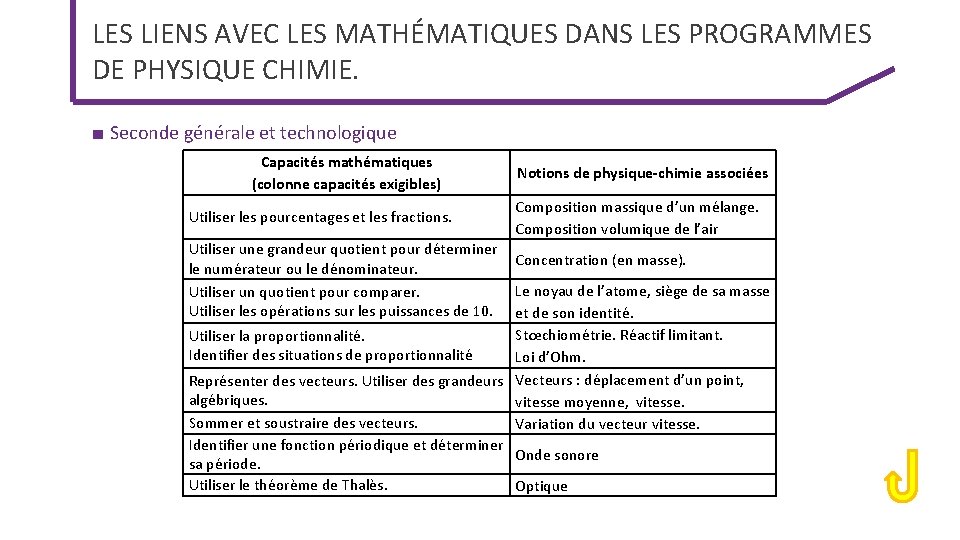
LES LIENS AVEC LES MATHÉMATIQUES DANS LES PROGRAMMES DE PHYSIQUE CHIMIE. ■ Seconde générale et technologique Capacités mathématiques (colonne capacités exigibles) Utiliser les pourcentages et les fractions. Utiliser une grandeur quotient pour déterminer le numérateur ou le dénominateur. Utiliser un quotient pour comparer. Utiliser les opérations sur les puissances de 10. Notions de physique-chimie associées Composition massique d’un mélange. Composition volumique de l’air Concentration (en masse). Le noyau de l’atome, siège de sa masse et de son identité. Stœchiométrie. Réactif limitant. Utiliser la proportionnalité. Identifier des situations de proportionnalité Loi d’Ohm. Représenter des vecteurs. Utiliser des grandeurs Vecteurs : déplacement d’un point, algébriques. vitesse moyenne, vitesse. Sommer et soustraire des vecteurs. Variation du vecteur vitesse. Identifier une fonction périodique et déterminer Onde sonore sa période. Utiliser le théorème de Thalès. Optique

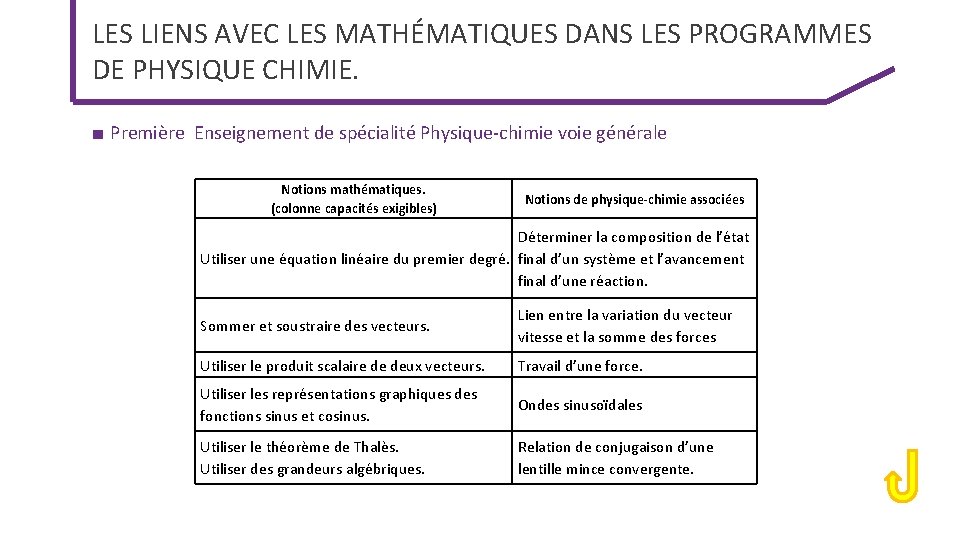
LES LIENS AVEC LES MATHÉMATIQUES DANS LES PROGRAMMES DE PHYSIQUE CHIMIE. ■ Première Enseignement de spécialité Physique-chimie voie générale Notions mathématiques. (colonne capacités exigibles) Notions de physique-chimie associées Déterminer la composition de l’état Utiliser une équation linéaire du premier degré. final d’un système et l’avancement final d’une réaction. Sommer et soustraire des vecteurs. Lien entre la variation du vecteur vitesse et la somme des forces Utiliser le produit scalaire de deux vecteurs. Travail d’une force. Utiliser les représentations graphiques des fonctions sinus et cosinus. Ondes sinusoïdales Utiliser le théorème de Thalès. Utiliser des grandeurs algébriques. Relation de conjugaison d’une lentille mince convergente.

LES LIENS AVEC LES MATHÉMATIQUES DANS LES PROGRAMMES DE PHYSIQUE CHIMIE. ■ Première STI 2 D Physique-chimie et Mathématiques Lien avec les mathématiques. (à la fin de chaque partie) Nombre dérivé. Fonctions périodiques, fonctions trigonométriques. Notions de physique-chimie associées Énergie. Tension électrique : • • Dérivées. Produit scalaire. Géométrie dans le plan. Grandeurs périodiques : valeurs moyenne, efficace, composantes continue et alternative. Grandeurs sinusoïdales. Ondes périodiques. Ondes sinusoïdales. Vitesse / accélération. Travail d’une force. Ondes.

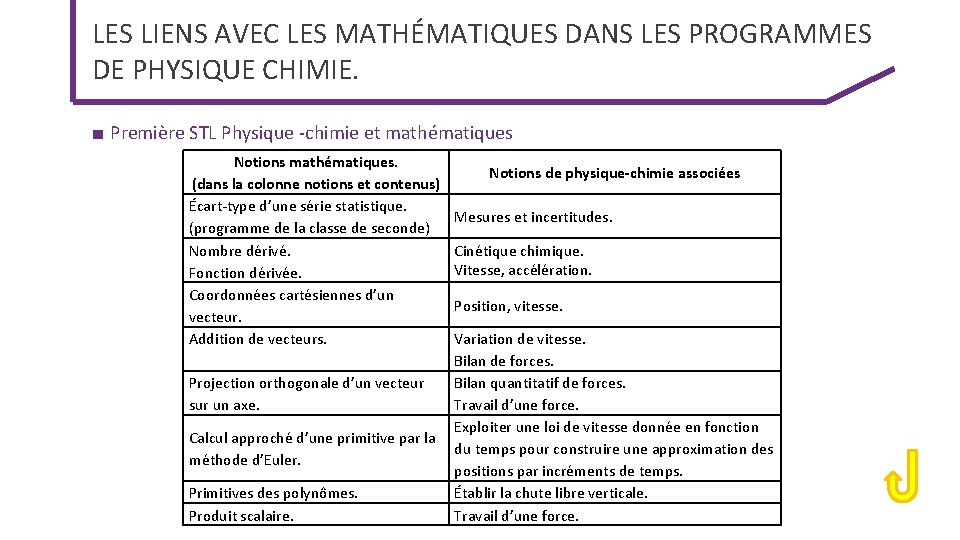
LES LIENS AVEC LES MATHÉMATIQUES DANS LES PROGRAMMES DE PHYSIQUE CHIMIE. ■ Première STL Physique -chimie et mathématiques Notions mathématiques. (dans la colonne notions et contenus) Écart-type d’une série statistique. (programme de la classe de seconde) Nombre dérivé. Fonction dérivée. Coordonnées cartésiennes d’un vecteur. Addition de vecteurs. Projection orthogonale d’un vecteur sur un axe. Calcul approché d’une primitive par la méthode d’Euler. Primitives des polynômes. Produit scalaire. Notions de physique-chimie associées Mesures et incertitudes. Cinétique chimique. Vitesse, accélération. Position, vitesse. Variation de vitesse. Bilan de forces. Bilan quantitatif de forces. Travail d’une force. Exploiter une loi de vitesse donnée en fonction du temps pour construire une approximation des positions par incréments de temps. Établir la chute libre verticale. Travail d’une force.