Mathmatiques CST CHAPITRE 1 LOPTIMISATION Mathmatiques CST OPTIMISATION
















- Slides: 28

Mathématiques CST CHAPITRE 1 L’OPTIMISATION

Mathématiques CST - OPTIMISATION Rappel sur les inéquations A) Traduction Exemple # 1 : À chaque année, Sébastien joue au moins 5 parties de hockey de plus que de parties de football. Variables x : Nombre de parties de hockey y : Nombre de parties de football Inéquation x ≥ y + 5

À chaque année, Sébastien joue au plus le double de parties de Exemple # 2 : À chaque année, Sébastien joue au plus le double de parties de hockey que de parties de football. Variables x : Nombre de parties de hockey y : Nombre de parties de football Inéquation x ≤ 2 y Exemple # 3 : Chez HMV, je dispose de 150 $ pour acheter des CD de musique à 10 $ chacun et des DVD de film à 18 $ chacun. Variables x : Nombre de CD de musique y : Nombre de DVD de film Inéquation 10 x + 18 y ≤ 150

Mathématiques CST - OPTIMISATION Rappel sur les inéquations B) Représentation graphique Exemple # 1 : Représenter graphiquement -2 y 4 x + 6.

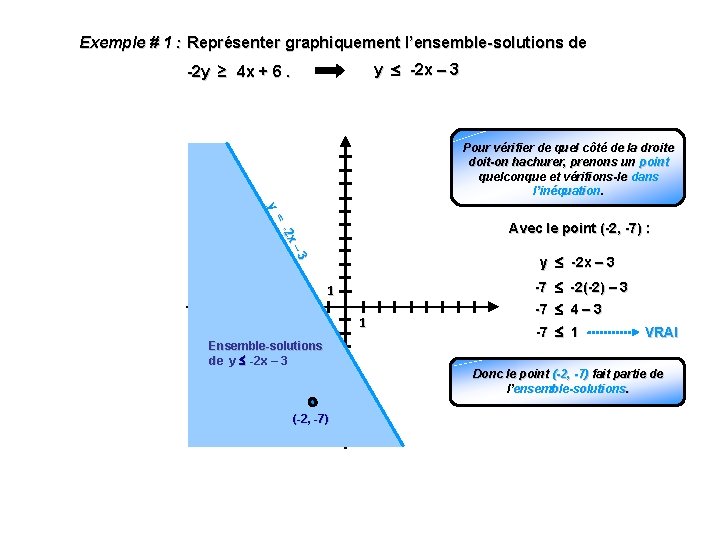
Exemple # 1 : Représenter graphiquement l’ensemble-solutions de y -2 x – 3 -2 y ≥ 4 x + 6. Pour vérifier de quel côté de la droite doit-on hachurer, prenons un point quelconque et vérifions-le dans l’inéquation. 3 – -2 x = y Avec le point (-2, -7) : y -2 x – 3 -7 -2(-2) – 3 1 1 Ensemble-solutions de y -2 x – 3 (-2, -7) -7 4 – 3 -7 1 VRAI Donc le point (-2, -7) fait partie de l’ensemble-solutions. .

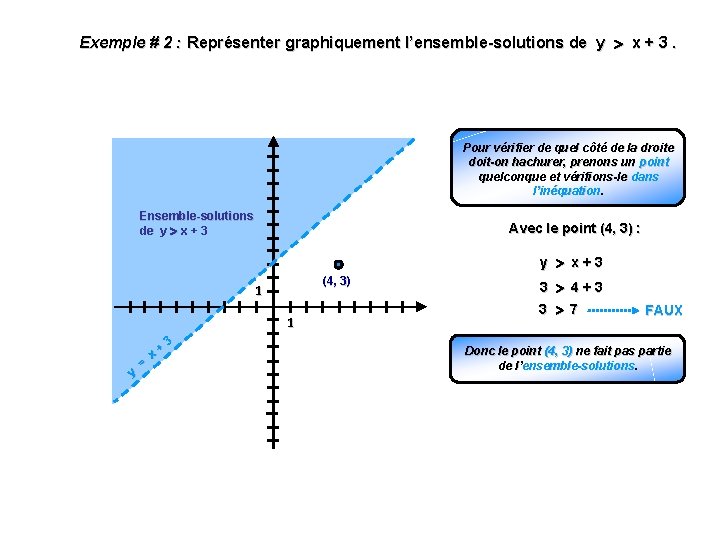
Exemple # 2 : Représenter graphiquement l’ensemble-solutions de y x + 3. Pour vérifier de quel côté de la droite doit-on hachurer, prenons un point quelconque et vérifions-le dans l’inéquation. Ensemble-solutions de y x + 3 Avec le point (4, 3) : y x + 3 (4, 3) 1 1 3 + x = y 3 4 + 3 3 7 F AUX Donc le point (4, 3) ne fait pas partie de l’ensemble-solutions. .

Mathématiques CST - OPTIMISATION Rappel sur les inéquations B) Représentation graphique En RÉSUMÉ… ou -----> Droite frontière pointillée ou -----> Droite frontière pleine y ou y -----> Ensemble-solutions au-dessus de la droite frontière y ou y -----> Ensemble-solutions en-dessous de la droite frontière

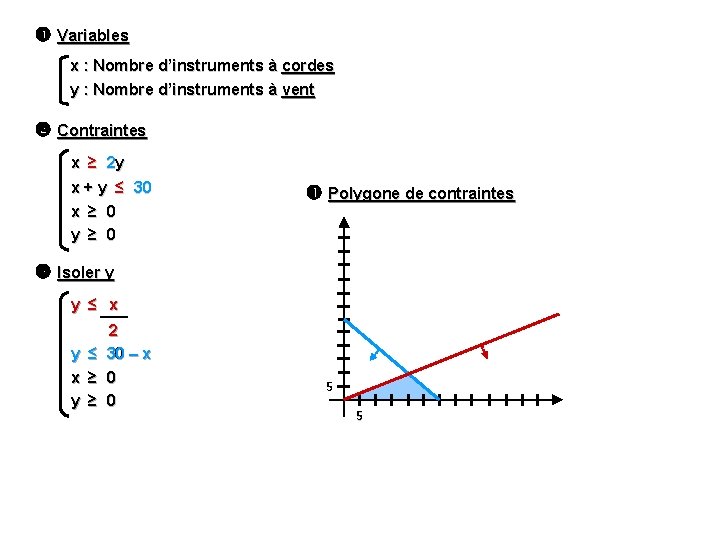
Mathématiques CST - OPTIMISATION Polygone de contraintes Exemple # 1 : Dans un orchestre, il y a des instruments à à cordes et à vent. Il y a au au moins 2 fois plus d’instruments à cordes que d’instruments à vent. . De plus, il y a au plus 30 30 musiciens. . Tracer le polygone de contraintes de cette situation. Variables x : Nombre d’instruments à cordes y : Nombre d’instruments à vent Contraintes x ≥ 2 y x + y ≤ 30 x ≥ 0 Contraintes de non-négativité y ≥ 0

Variables x : Nombre d’instruments à cordes y : Nombre d’instruments à vent Contraintes x ≥ 2 y x + y ≤ 30 x ≥ 0 y ≥ 0 Polygone de contraintes Isoler y y ≤ x 2 y ≤ 30 – x x ≥ 0 y ≥ 0 5 5

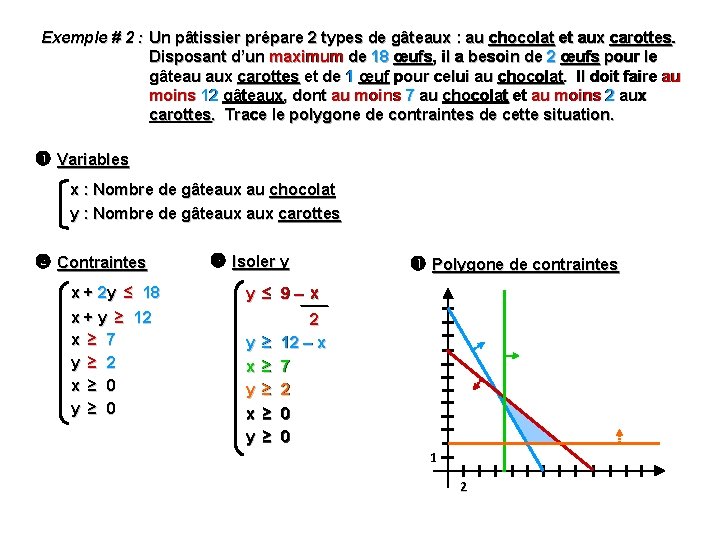
Exemple # 2 : Un pâtissier prépare 2 types de gâteaux : au chocolat et aux carottes. Disposant d’un maximum de 18 œufs, il a besoin de 2 œufs pour le gâteau aux carottes et de 1 œuf pour celui au chocolat. Il doit faire au moins 12 gâteaux, dont au moins 7 au chocolat et au moins 2 aux carottes. Trace le polygone de contraintes de cette situation. Variables x : Nombre de gâteaux au chocolat y : Nombre de gâteaux carottes Contraintes Isoler y x + 2 y ≤ 18 y ≤ 9 – x x + y ≥ 12 x ≥ 7 y ≥ 2 x ≥ 0 y ≥ 0 2 y ≥ 12 – x x ≥ 7 y ≥ 2 x ≥ 0 y ≥ 0 Polygone de contraintes 1 2

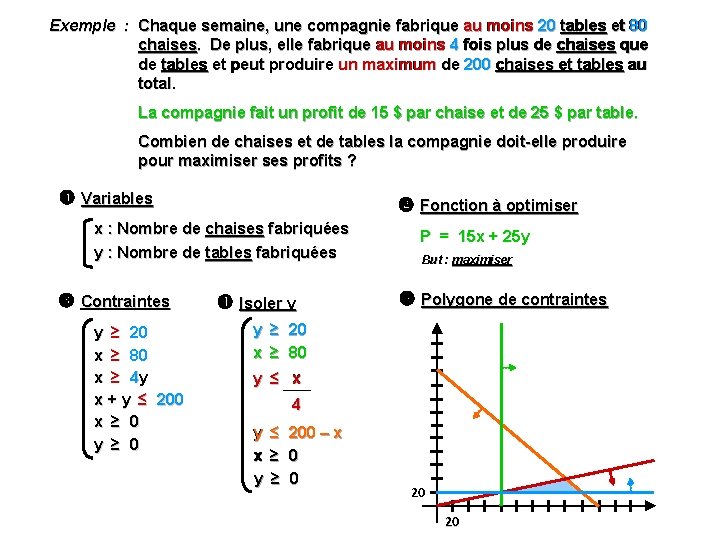
Mathématiques CST - OPTIMISATION Fonction à optimiser Chaque semaine, une compagnie fabrique au moins 20 tables et 80 Exemple : Chaque semaine, une compagnie fabrique au moins 20 tables et 80 chaises. De plus, elle fabrique au moins 4 fois plus de chaises que de tables et peut produire un maximum de 200 chaises et tables au total. La compagnie fait un profit de 15 $ par chaise et de 25 $ par table. Combien de chaises et de tables la compagnie doit-elle produire pour maximiser ses profits ? Variables Fonction à optimiser x : Nombre de chaises P = 15 x + 25 y fabriquées y : Nombre de tables But : maximiser fabriquées Règle qui traduit le but visé par une fonction.

Chaque semaine, une compagnie fabrique au moins 20 tables et 80 Exemple : Chaque semaine, une compagnie fabrique au moins 20 tables et 80 chaises. De plus, elle fabrique au moins 4 fois plus de chaises que de tables et peut produire un maximum de 200 chaises et tables au total. La compagnie fait un profit de 15 $ par chaise et de 25 $ par table. Combien de chaises et de tables la compagnie doit-elle produire pour maximiser ses profits ? Variables Fonction à optimiser x : Nombre de chaises fabriquées y : Nombre de tables fabriquées Contraintes y ≥ 20 x ≥ 80 x ≥ 4 y x + y ≤ 200 x ≥ 0 y ≥ 0 Isoler y P = 15 x + 25 y But : maximiser Polygone de contraintes y ≥ 20 x ≥ 80 y ≤ x 4 y ≤ 200 – x x ≥ 0 y ≥ 0 20 20

Mathématiques CST - OPTIMISATION Recherche de la solution optimale Polygone de contraintes Coordonnées des sommets A : y = 20 x = 80 B : y = 200 – x (1) y = x (2) A (80, 20) 4 20 20 (3) dans (1) : 200 – x = x y = 200 – 160 4 200 = 5 x B A (1) = (2) : 4 C y = 40 B (160, 40) 160 = x (3) C : y = 20 (1) y = 200 – x (2) (1) = (2) : 200 – x = 20 - x = - 180 x = 180 C (180, 20)

Tableau-solutions Sommets P = 15 x + 25 y Profits A (80, 20) P = 15(80) + 25(20) 1700 $ B (160, 40) P = 15(160) + 25(40) 3400 $ C (180, 20) P = 15(180) + 25(20) 3200 $ Maximum Solution Pour réaliser un profit maximal, la compagnie doit fabriquer 160 chaises et 40 tables.

Mathématiques CST - OPTIMISATION Structure d’un problème d’optimisation complet Variables Polygone de contraintes Fonction à optimiser Coordonnées des sommets Contraintes Tableau-solutions Isoler y Solution

Une entreprise confectionne 2 produits différents : des foulards et Exemple : Une entreprise confectionne 2 produits différents : des foulards et des chandails. Un foulard demande 8 heures pour la préparation des modèles et 4 heures pour l’impression. Quant aux chandails, il faut 2 heures pour concevoir les modèles et 15 minutes pour l’impression. Chaque semaine, il faut fabriquer de 20 à 80 foulards et de 100 à 250 chandails. Il y a 30 personnes qui travaillent 40 heures par semaine : 22 personnes pour les modèles et 8 personnes pour l’impression. L’entreprise fait des profits de 20 $ par foulard et de 4 $ par chandail. Combien d’articles de chaque sorte la compagnie doit-elle vendre pour maximiser ses profits ? Variables x : Nombre de foulards produits par semaine y : Nombre de chandails produits par semaine Fonction à optimiser P = 20 x + 4 y But : maximiser

Exemple : Une entreprise confectionne 2 produits différents : des foulards et des chandails. Un foulard demande 8 heures pour la préparation des modèles et 4 heures pour l’impression. Quant aux chandails, il faut 2 heures pour concevoir les modèles et 15 minutes pour l’impression. Chaque semaine, il faut fabriquer de 20 à 80 foulards et de 100 à 250 chandails. Il y a 30 personnes qui travaillent 40 heures par semaine : 22 personnes pour les modèles et 8 personnes pour l’impression. L’entreprise fait des profits de 20 $ par foulard et de 4 $ par chandail. Combien d’articles de chaque sorte la compagnie doit-elle vendre pour maximiser ses profits ? Contraintes Isoler y x ≥ 20 x ≤ 80 y ≥ 100 y ≤ 250 8 x + 2 y ≤ 880 4 x + 0, 25 y ≤ 320 x ≥ 0 y ≥ 0 x ≥ 20 22 personnes x 40 heures = 880 heures 8 personnes x 40 heures = 320 heures x ≤ 80 y ≥ 100 y ≤ 250 y ≤ 440 – 4 x y ≤ 1280 – 16 x x ≥ 0 y ≥ 0

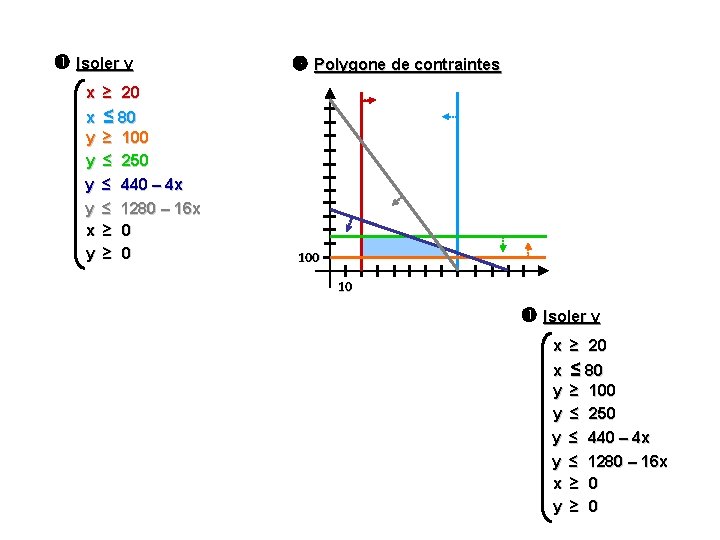
Isoler y Polygone de contraintes x ≥ 20 x ≤ 80 y ≥ 100 y ≤ 250 y ≤ 440 – 4 x y ≤ 1280 – 16 x x ≥ 0 y ≥ 0 10 Isoler y x ≥ 20 x ≤ 80 y ≥ 100 y ≤ 250 y ≤ 440 – 4 x y ≤ 1280 – 16 x x ≥ 0 y ≥ 0

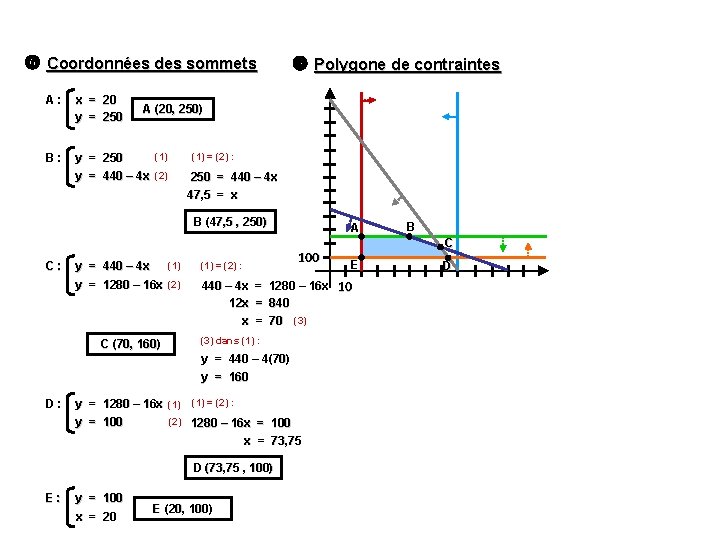
Coordonnées des sommets A : x = 20 y = 250 B : (1) y = 250 y = 440 – 4 x (2) Polygone de contraintes A (20, 250) (1) = (2) : 250 = 440 – 4 x 47, 5 = x B (47, 5 , 250) C : (1) y = 440 – 4 x y = 1280 – 16 x (2) C (70, 160) (1) = (2) : A 100 y = 440 – 4(70) y = 160 D : y = 1280 – 16 x (1) = (2) : (2) 1280 – 16 x = 100 y = 100 x = 73, 75 D (73, 75 , 100) E : y = 100 x = 20 C E 440 – 4 x = 1280 – 16 x 10 12 x = 840 x = 70 (3) dans (1) : E (20, 100) B D

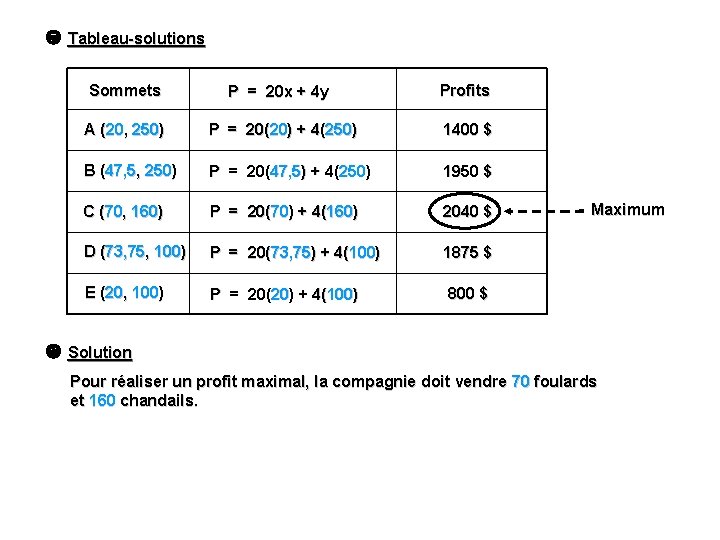
Tableau-solutions Sommets P = 20 x + 4 y Profits A (20, 250) P = 20(20) + 4(250) 1400 $ B (47, 5, 250) P = 20(47, 5) + 4(250) 1950 $ C (70, 160) P = 20(70) + 4(160) 2040 $ D (73, 75, 100) P = 20(73, 75) + 4(100) 1875 $ E (20, 100) P = 20(20) + 4(100) 800 $ Maximum Solution Pour réaliser un profit maximal, la compagnie doit vendre 70 foulards et 160 chandails.

Mathématiques CST - OPTIMISATION Test formatif #1 Dans une petite ville, on offre aux habitants 2 types de transport : en train ou en autobus. Cependant, la ville peut offrir un maximum de 30 transports par jour, dont au plus 20 voyages en train par jour. De plus, elle souhaite que le nombre de voyages en train soit supérieur d’au moins 1 fois et demi ceux par autobus. Comme elle tire des revenus de 90$ par voyage en train et de 60$ par voyage en autobus, combien de transport de chaque type doit-elle effectuer pour maximiser ses revenus ?

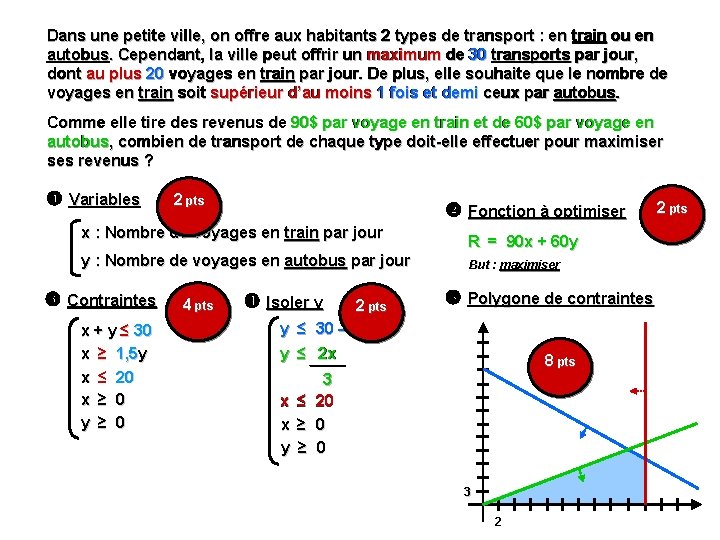
Dans une petite ville, on offre aux habitants 2 types de transport : en train ou en autobus. Cependant, la ville peut offrir un maximum de 30 transports par jour, dont au plus 20 voyages en train par jour. De plus, elle souhaite que le nombre de voyages en train soit supérieur d’au moins 1 fois et demi ceux par autobus. Comme elle tire des revenus de 90$ par voyage en train et de 60$ par voyage en autobus, combien de transport de chaque type doit-elle effectuer pour maximiser ses revenus ? Variables 2 pts Fonction à optimiser x : Nombre de voyages en train par jour y : Nombre de voyages en autobus par jour Contraintes x + y ≤ 30 x ≥ 1, 5 y x ≤ 20 x ≥ 0 y ≥ 0 4 pts Isoler y 2 pts y ≤ 30 – x R = 90 x + 60 y But : maximiser Polygone de contraintes y ≤ 2 x 8 pts 3 x ≤ 20 x ≥ 0 y ≥ 0 3 2 2 pts

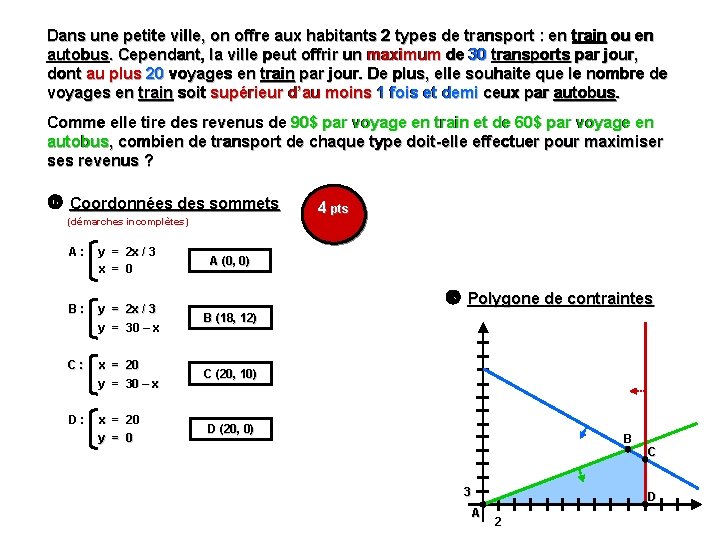
Dans une petite ville, on offre aux habitants 2 types de transport : en train ou en autobus. Cependant, la ville peut offrir un maximum de 30 transports par jour, dont au plus 20 voyages en train par jour. De plus, elle souhaite que le nombre de voyages en train soit supérieur d’au moins 1 fois et demi ceux par autobus. Comme elle tire des revenus de 90$ par voyage en train et de 60$ par voyage en autobus, combien de transport de chaque type doit-elle effectuer pour maximiser ses revenus ? Coordonnées des sommets (démarches incomplètes) A : y = 2 x / 3 x = 0 B : y = 2 x / 3 y = 30 – x B (18, 12) C : x = 20 y = 30 – x C (20, 10) D : x = 20 y = 0 4 pts A (0, 0) Polygone de contraintes D (20, 0) B 3 C D A 2

Dans une petite ville, on offre aux habitants 2 types de transport : en train ou en autobus. Cependant, la ville peut offrir un maximum de 30 transports par jour, dont au plus 20 voyages en train par jour. De plus, elle souhaite que le nombre de voyages en train soit supérieur d’au moins 1 fois et demi ceux par autobus. Comme elle tire des revenus de 90$ par voyage en train et de 60$ par voyage en autobus, combien de transport de chaque type doit-elle effectuer pour maximiser ses revenus ? Tableau-solutions Sommets 2 pts R = 90 x + 60 y Revenus A (0, 0) R = 90(0) + 60(0) B (18, 12) R = 90(18) + 60(12) 2340 $ C (20, 10) R = 90(20) + 60(10) 2400 $ D (20, 0) R = 90(20) + 60(0) 1800 $ Solution 0 $ Maximum 1 pt Pour maximiser ses revenus, la ville doit effectuer 20 voyages en train et 10 voyages en autobus.

Mathématiques CST - OPTIMISATION Test formatif #2 Dans un quartier d’une ville, on offre des cours de réparation de vélo qui sont limités à un maximum de 12 participants et participantes. Il y a deux types de cours offerts : un cours pour personnes débutantes, qui dure une heure et coûte 16 $, et un cours avancé, qui dure deux heures trente minutes et coûte 12 $. La municipalité prête l’équipement requis pour un maximum de 18 heures par semaine. Il a été établi que le nombre d’inscriptions au cours avancé doit être au plus égal au double de celui du cours pour novices. Si la municipalité souhaite maximiser ses revenus, combien de personnes faudrait-il accepter dans chacun des cours ?

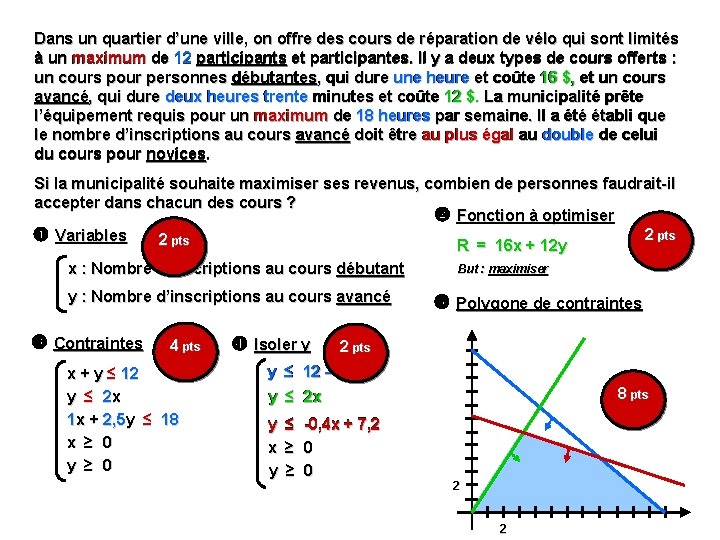
Dans un quartier d’une ville, on offre des cours de réparation de vélo qui sont limités à un maximum de 12 participants et participantes. Il y a deux types de cours offerts : un cours pour personnes débutantes, qui dure une heure et coûte 16 $, et un cours avancé , qui dure deux heures trente minutes et coûte 12 $. La municipalité prête avancé, qui dure deux heures trente minutes et coûte 12 $. La municipalité prête l’équipement requis pour un maximum de 18 heures par semaine. Il a été établi que le nombre d’inscriptions au cours avancé doit être au plus égal au double de celui du cours pour novices. Si la municipalité souhaite maximiser ses revenus, combien de personnes faudrait-il accepter dans chacun des cours ? Fonction à optimiser 2 pts Variables 2 pts R = 16 x + 12 y x : Nombre d’inscriptions au cours débutant y : Nombre d’inscriptions au cours avancé Contraintes 4 pts x + y ≤ 12 y ≤ 2 x 1 x + 2, 5 y ≤ 18 x ≥ 0 y ≥ 0 Isoler y But : maximiser Polygone de contraintes 2 pts y ≤ 12 – x 8 pts y ≤ 2 x y ≤ -0, 4 x + 7, 2 x ≥ 0 y ≥ 0 2 2

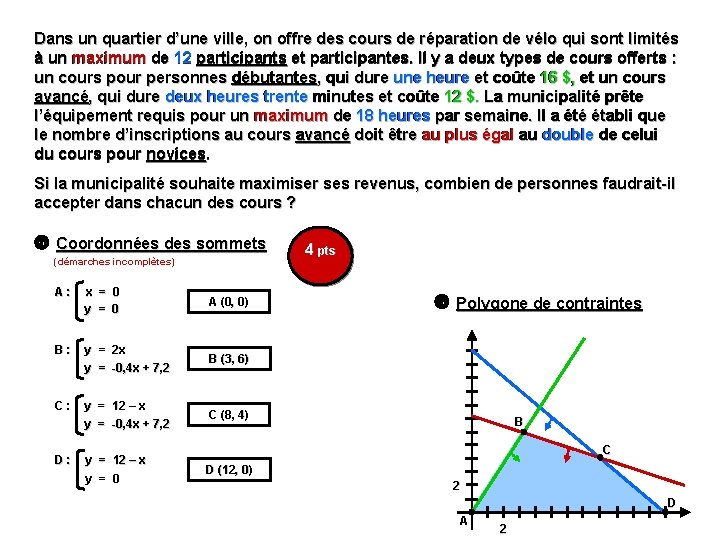
Dans un quartier d’une ville, on offre des cours de réparation de vélo qui sont limités à un maximum de 12 participants et participantes. Il y a deux types de cours offerts : un cours pour personnes débutantes, qui dure une heure et coûte 16 $, et un cours avancé , qui dure deux heures trente minutes et coûte 12 $. La municipalité prête avancé, qui dure deux heures trente minutes et coûte 12 $. La municipalité prête l’équipement requis pour un maximum de 18 heures par semaine. Il a été établi que le nombre d’inscriptions au cours avancé doit être au plus égal au double de celui du cours pour novices. Si la municipalité souhaite maximiser ses revenus, combien de personnes faudrait-il accepter dans chacun des cours ? Coordonnées des sommets (démarches incomplètes) A : x = 0 y = 0 A (0, 0) B : y = 2 x y = -0, 4 x + 7, 2 B (3, 6) C : y = 12 – x y = -0, 4 x + 7, 2 C (8, 4) D : y = 12 – x y = 0 4 pts Polygone de contraintes B C D (12, 0) 2 D A 2

Dans un quartier d’une ville, on offre des cours de réparation de vélo qui sont limités à un maximum de 12 participants et participantes. Il y a deux types de cours offerts : un cours pour personnes débutantes, qui dure une heure et coûte 16 $, et un cours avancé , qui dure deux heures trente minutes et coûte 12 $. La municipalité prête avancé, qui dure deux heures trente minutes et coûte 12 $. La municipalité prête l’équipement requis pour un maximum de 18 heures par semaine. Il a été établi que le nombre d’inscriptions au cours avancé doit être au plus égal au double de celui du cours pour novices. Si la municipalité souhaite maximiser ses revenus, combien de personnes faudrait-il accepter dans chacun des cours ? Tableau-solutions Sommets 2 pts R = 16 x + 12 y Revenus A (0, 0) R = 16(0) + 12(0) 0 $ B (3, 6) R = 16(3) + 12(6) 120 $ C (8, 4) R = 16(8) + 12(4) 176 $ D (12, 0) R = 16(12) + 12(0) 192 $ Solution Maximum 1 pt Pour maximiser ses revenus, il faut 12 inscriptions au cours débutant et aucune inscription au cours avancé.