Mathmatiques CST Optimisation de GRAPHES Mathmatiques CST Loptimisation

Mathématiques CST Optimisation de GRAPHES

Mathématiques CST - L’optimisation de GRAPHES Arbre de valeurs minimales et maximales Arbre qui relie tous les sommets du graphe par une sélection d’arêtes pour que le poids de l’arbre soit le plus petit possible (minimal) ou le plus grand possible (maximal). MÉTHODE : Algorithme de Kruskal 1. Énumérer toutes les arêtes et les placer en ordre croissant de poids (arbre de valeurs minimales). 2. Choisir l’arête ayant le plus petit poids. 3. Répéter l’étape 2 jusqu’à ce que tous les sommets soient reliés en évitant celles qui formeraient un cycle simple.

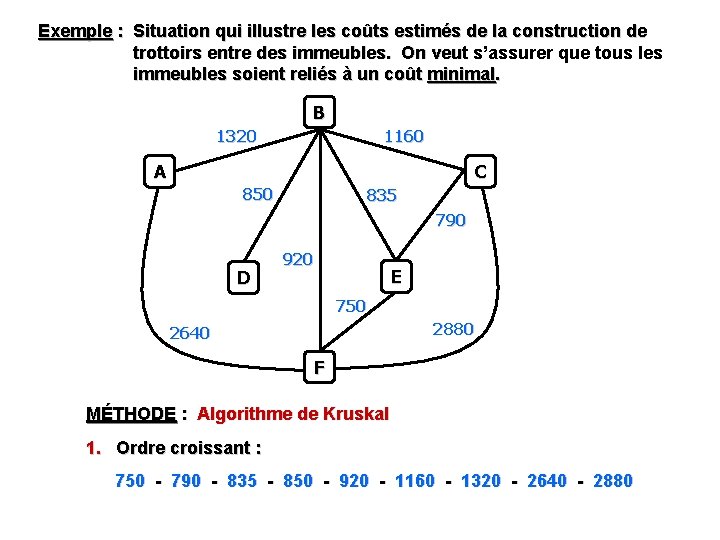
Exemple : Situation qui illustre les coûts estimés de la construction de trottoirs entre des immeubles. On veut s’assurer que tous les immeubles soient reliés à un coût minimal. B 1320 1160 A C 850 835 790 D 920 E 750 2880 2640 F MÉTHODE : Algorithme de Kruskal 1. Ordre croissant : 750 - 790 - 835 - 850 - 920 - 1160 - 1320 - 2640 - 2880

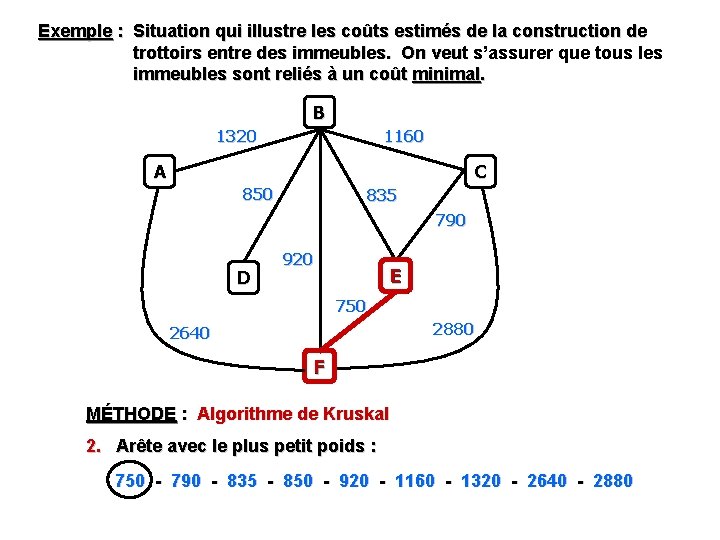
Exemple : Situation qui illustre les coûts estimés de la construction de trottoirs entre des immeubles. On veut s’assurer que tous les immeubles sont reliés à un coût minimal. B 1320 1160 A C 850 835 790 D 920 E 750 2880 2640 F MÉTHODE : Algorithme de Kruskal 2. Arête avec le plus petit poids : 750 - 790 - 835 - 850 - 920 - 1160 - 1320 - 2640 - 2880

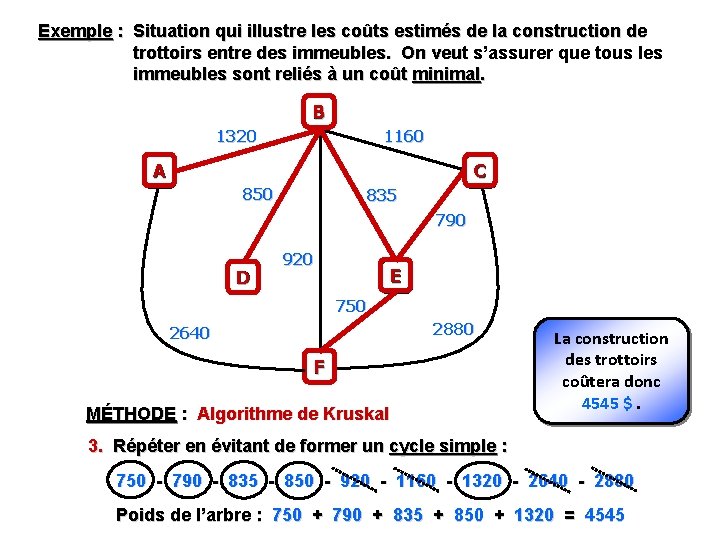
Exemple : Situation qui illustre les coûts estimés de la construction de trottoirs entre des immeubles. On veut s’assurer que tous les immeubles sont reliés à un coût minimal. B 1320 1160 C A 850 835 790 D 920 E 750 2880 2640 F MÉTHODE : Algorithme de Kruskal La construction des trottoirs coûtera donc 4545 $. 3. Répéter en évitant de former un cycle simple : 750 - 790 - 835 - 850 - 920 - 1160 - 1320 - 2640 - 2880 Poids de l’arbre : 750 + 790 + 835 + 850 + 1320 = 4545

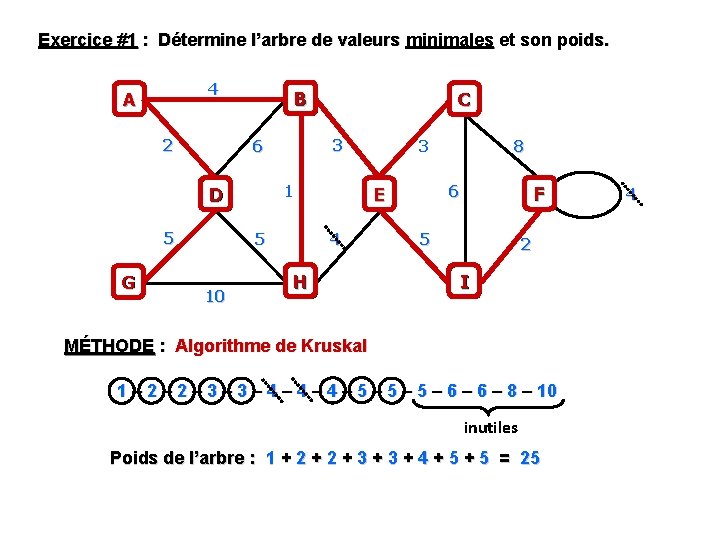
Exercice #1 : Détermine l’arbre de valeurs minimales et son poids. 4 A 2 B 1 D G 3 6 5 5 10 C 3 6 E 4 H 8 F 5 2 I MÉTHODE : Algorithme de Kruskal 1 – 2 – 3 – 4 – 4 – 5 – 5 – 6 – 8 – 10 inutiles Poids de l’arbre : 1 + 2 + 3 + 4 + 5 = 25 4

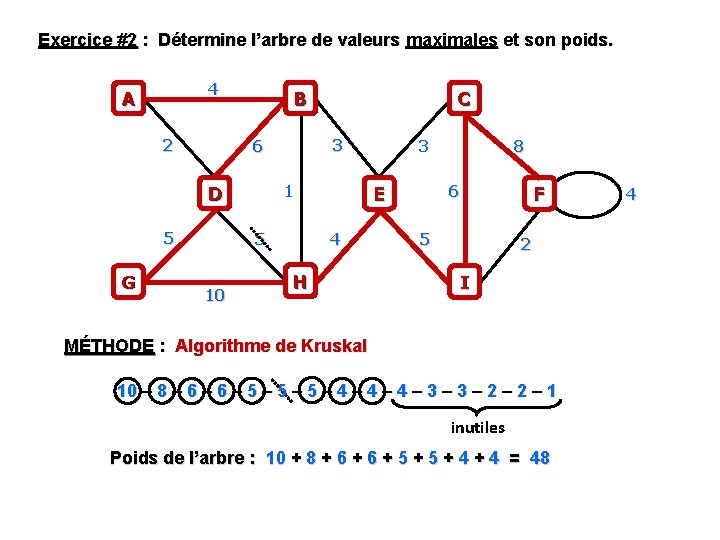
Exercice #2 : Détermine l’arbre de valeurs maximales et son poids. 4 A 2 B 1 D G 3 6 5 5 10 C 3 6 E 4 H 8 F 5 2 I MÉTHODE : Algorithme de Kruskal 10 – 8 – 6 – 5 – 5 – 4 – 4 – 3 – 2 – 1 inutiles Poids de l’arbre : 10 + 8 + 6 + 5 + 4 = 48 4

Mathématiques CST - L’optimisation de GRAPHES Chaîne de poids minimal Chaîne qui a la plus petite valeur. MÉTHODE : Algorithme de Dijkstra 1. On assigne à chaque sommet un nombre et une lettre. Nombre : distance la plus courte Lettre : sommet précédent d’où provient la chaîne 2. Répéter l’étape 1 jusqu’au dernier sommet. 3. Identifier la chaîne la plus courte par une lecture à rebours.

Exemple : Situation où les arêtes représentent des chemins et les sommets, des lieux. Trouver le chemin le plus court du point A à F. 7 2 (A) B 4 6 (B) D 2 4 4 A 9 (E) 3 2 F 4 7 C 5 E E 5 (B) 6 (B) Chaîne la plus courte : ABEF Poids : 9

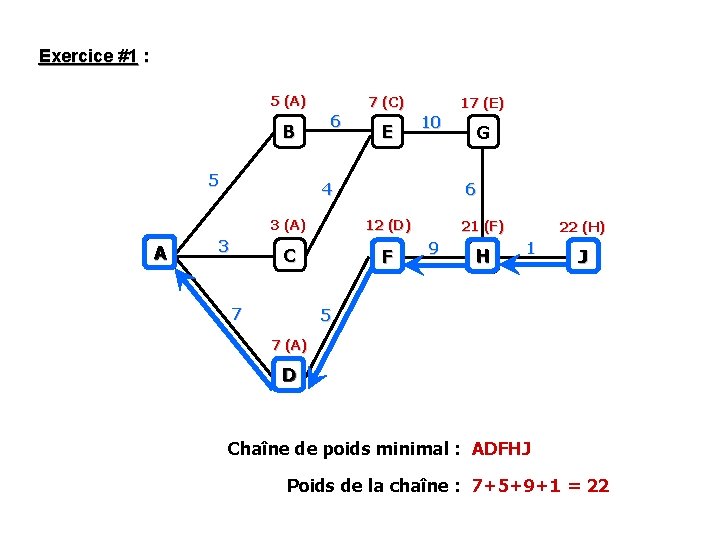
Exercice #1 : 5 (A) B 5 A 7 (C) 6 E 17 (E) 10 4 3 6 3 (A) 12 (D) C F 7 G 21 (F) 9 H 22 (H) 1 J 5 7 (A) D Chaîne de poids minimal : ADFHJ Poids de la chaîne : 7+5+9+1 = 22

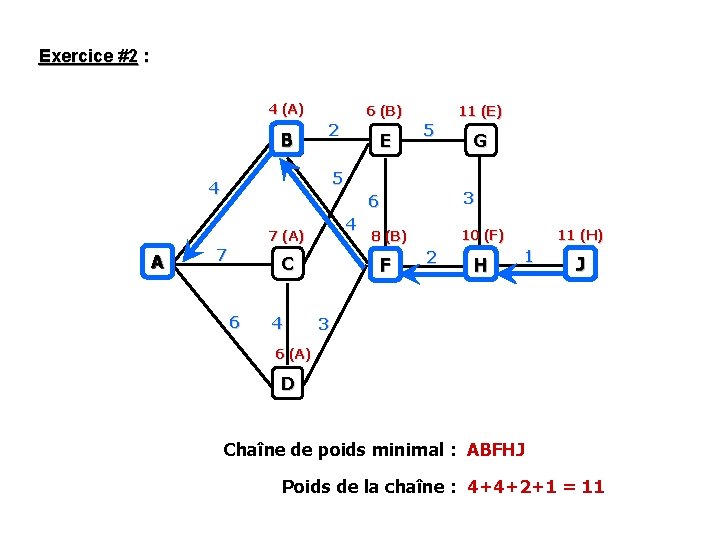
Exercice #2 : 4 (A) B 6 (B) 2 5 5 4 4 7 (A) A E 11 (E) 7 C 6 4 G 6 3 8 (B) 10 (F) F 2 H 11 (H) 1 J 3 6 (A) D Chaîne de poids minimal : ABFHJ Poids de la chaîne : 4+4+2+1 = 11

Mathématiques CST - L’optimisation de GRAPHES Chemin critique Pour réaliser une tâche (bâtir une maison, faire une recette, construire un avion, etc. ), on doit souvent réaliser plusieurs étapes. Certaines étapes doivent obligatoirement être faites avant certaines autres tandis que plusieurs étapes peuvent se faire en même temps (par des personnes ou des équipes différentes). Le chemin critique, c’est le temps minimum requis pour exécuter la tâche. Malheureusement, on doit attendre que certaines étapes soient terminées avant de passer aux étapes suivantes. Donc, c’est la chaîne ayant la plus grande valeur entre le début et la fin du projet.

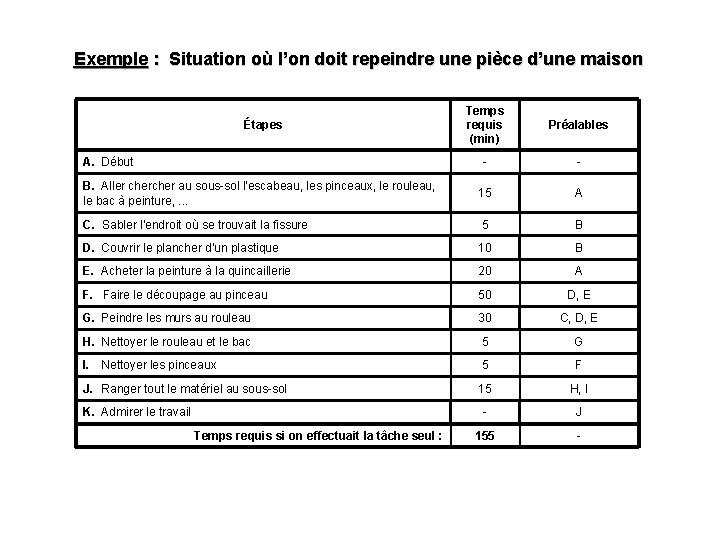
Exemple : Situation où l’on doit repeindre une pièce d’une maison Temps requis (min) Préalables - - B. Aller cher au sous-sol l'escabeau, les pinceaux, le rouleau, le bac à peinture, . . . 15 A C. Sabler l'endroit où se trouvait la fissure 5 B D. Couvrir le plancher d'un plastique 10 B E. Acheter la peinture à la quincaillerie 20 A F. Faire le découpage au pinceau 50 D, E G. Peindre les murs au rouleau 30 C, D, E H. Nettoyer le rouleau et le bac 5 G I. Nettoyer les pinceaux 5 F J. Ranger tout le matériel au sous-sol 15 H, I - J 155 - Étapes A. Début K. Admirer le travail Temps requis si on effectuait la tâche seul :

Graphe de la situation : Étapes A. Début A Temps requis (min) Préalables - -

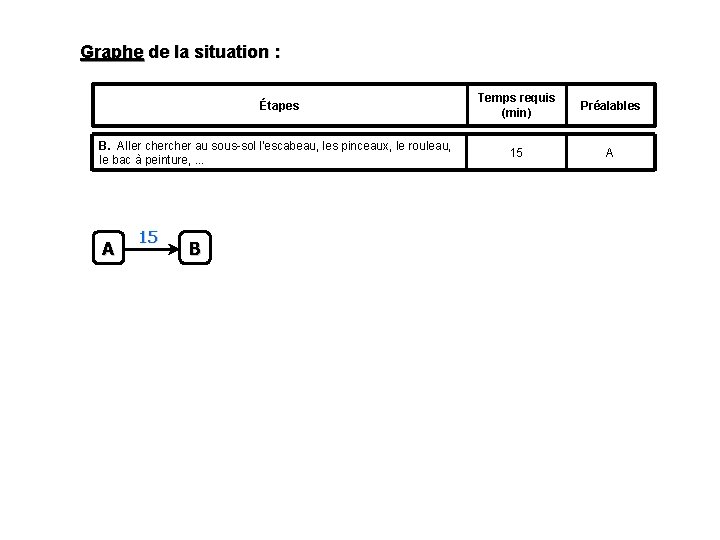
Graphe de la situation : Étapes B. Aller cher au sous-sol l'escabeau, les pinceaux, le rouleau, le bac à peinture, . . . A 15 B Temps requis (min) Préalables 15 A

Graphe de la situation : Étapes C. Sabler l'endroit où se trouvait la fissure A 15 B 5 C Temps requis (min) Préalables 5 B

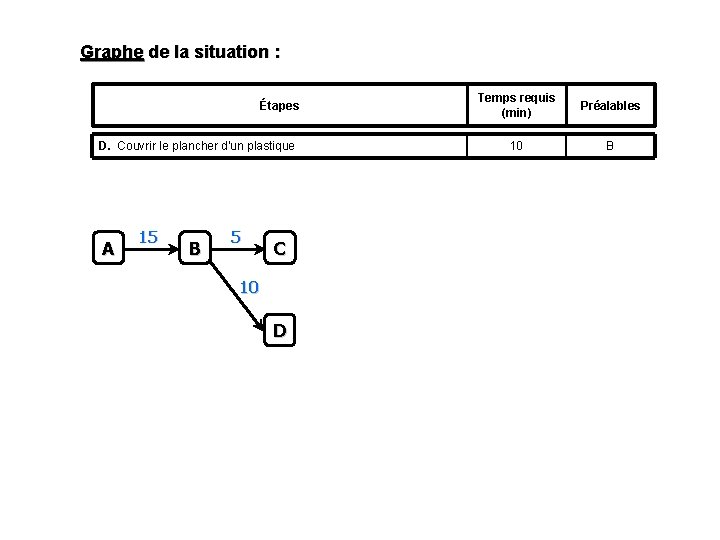
Graphe de la situation : Étapes D. Couvrir le plancher d'un plastique A 15 B 5 C 10 D Temps requis (min) Préalables 10 B

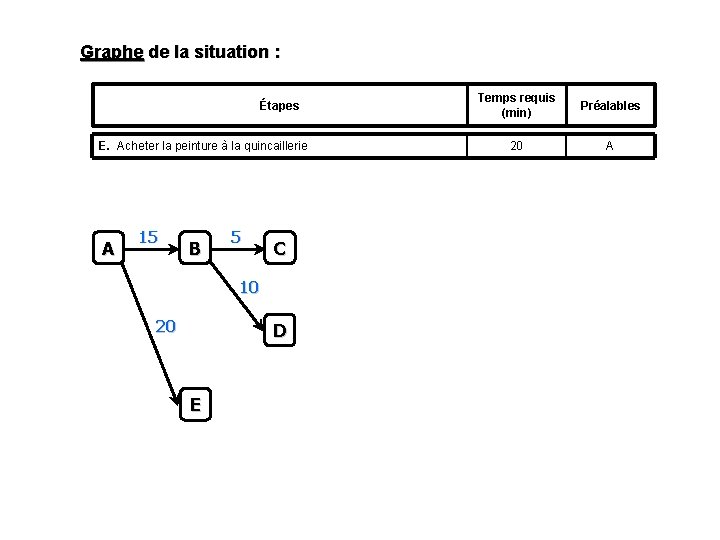
Graphe de la situation : Étapes E. Acheter la peinture à la quincaillerie A 15 B 5 C 10 20 D E Temps requis (min) Préalables 20 A

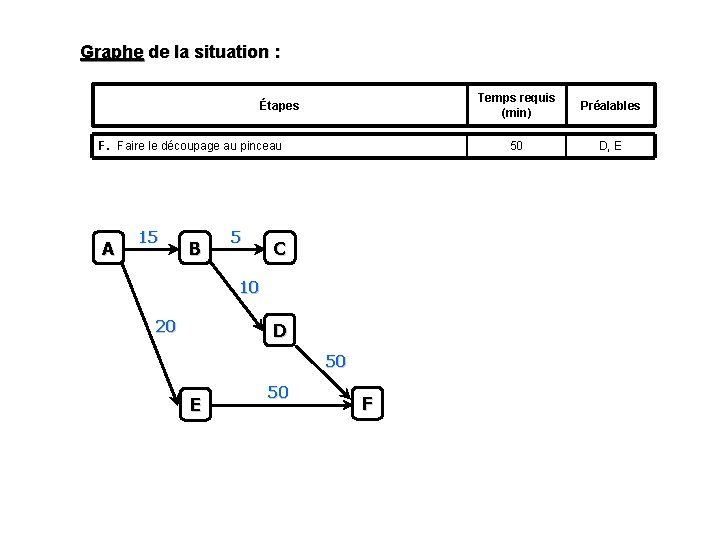
Graphe de la situation : Étapes F. Faire le découpage au pinceau A 15 B 5 C 10 20 D 50 E 50 F Temps requis (min) Préalables 50 D, E

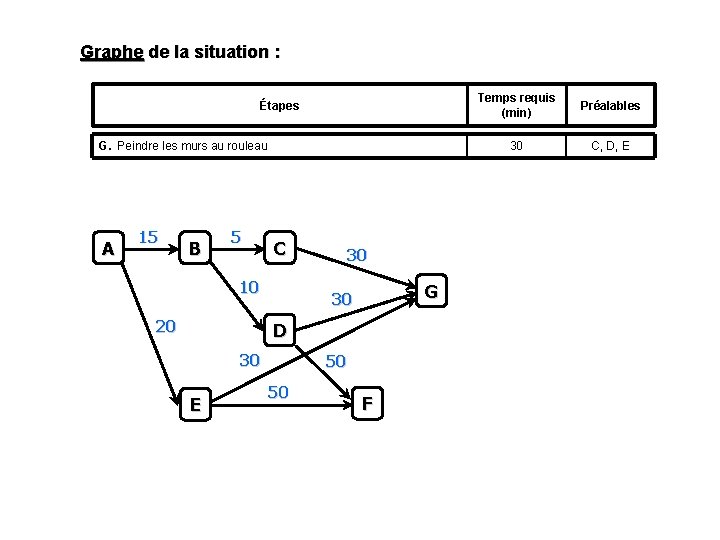
Graphe de la situation : Étapes G. Peindre les murs au rouleau A 15 B 5 C 10 20 30 G 30 D 30 E 50 50 F Temps requis (min) Préalables 30 C, D, E

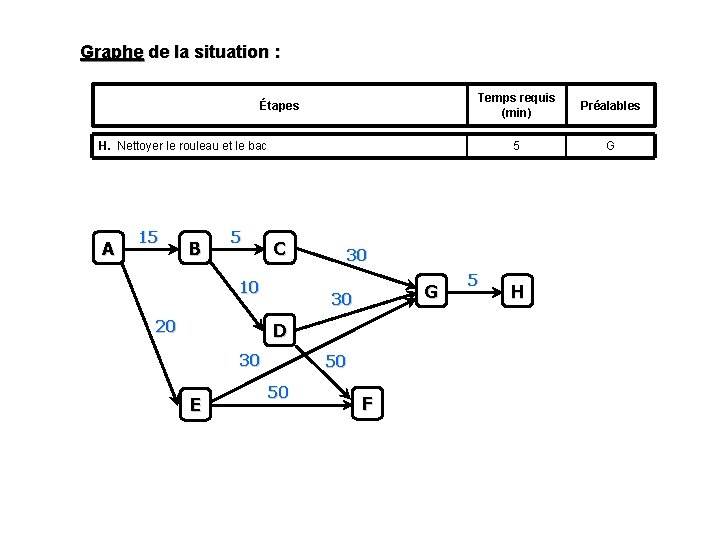
Graphe de la situation : Étapes Temps requis (min) Préalables 5 G H. Nettoyer le rouleau et le bac A 15 B 5 C 10 20 30 G 30 D 30 E 50 50 F 5 H

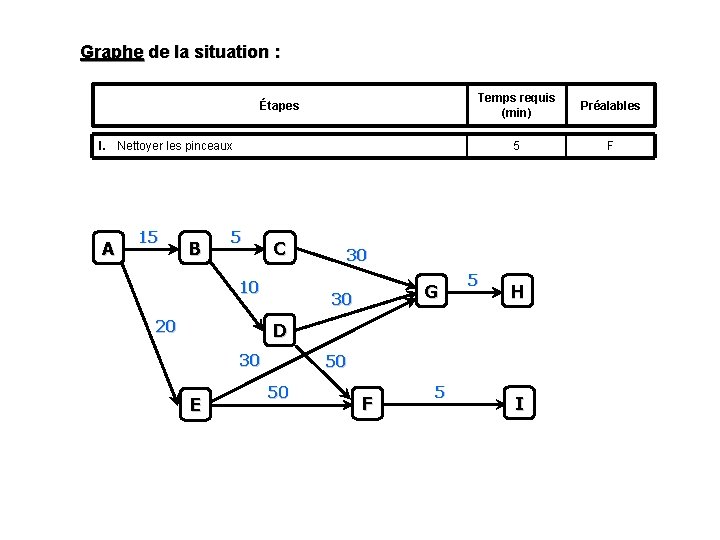
Graphe de la situation : Étapes Temps requis (min) Préalables 5 F I. Nettoyer les pinceaux A 15 B 5 C 10 20 30 G 30 5 H D 30 E 50 50 F 5 I

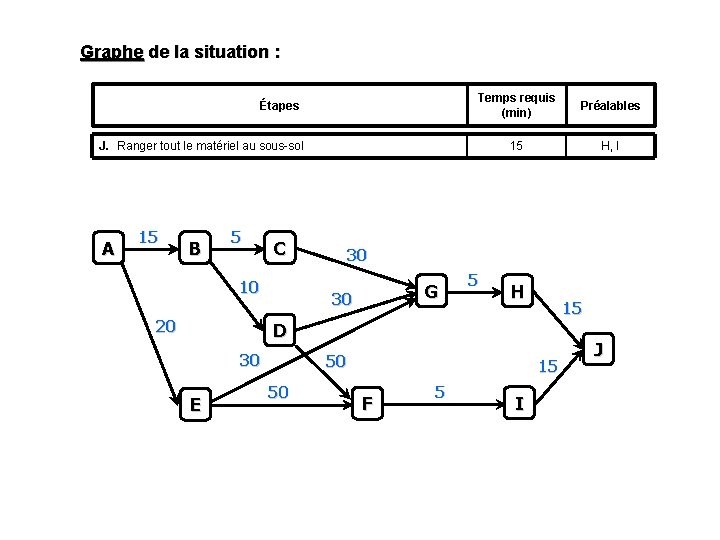
Graphe de la situation : Étapes Temps requis (min) Préalables 15 H, I J. Ranger tout le matériel au sous-sol A 15 B 5 C 10 20 30 G 30 5 H 15 D 30 E 50 50 15 F 5 I J

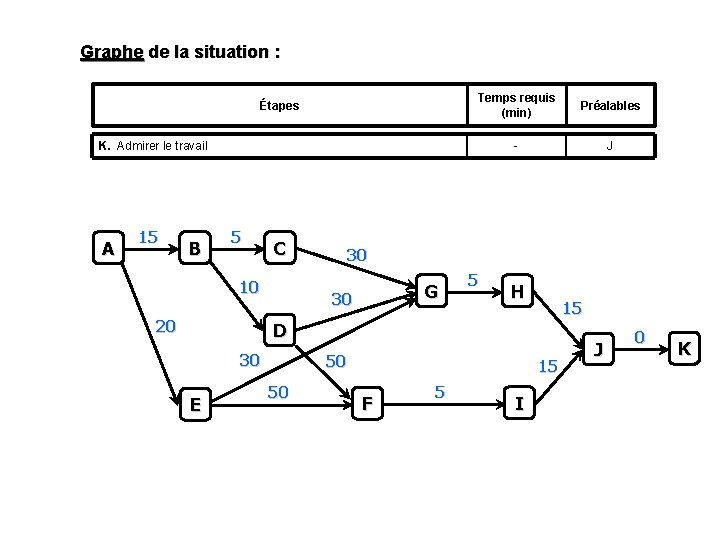
Graphe de la situation : Étapes Temps requis (min) Préalables - J K. Admirer le travail A 15 B 5 C 10 20 30 G 30 5 H 15 D 30 E 50 50 15 F 5 I J 0 K

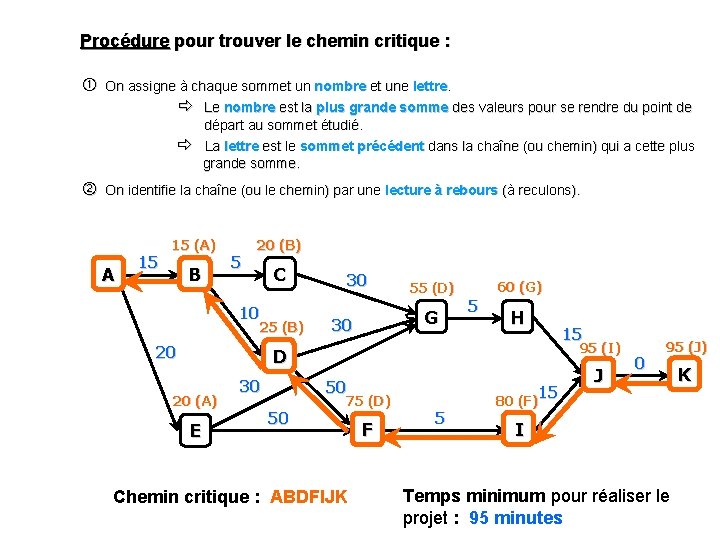
Procédure pour trouver le chemin critique : On assigne à chaque sommet un nombre et une lettre. Le nombre est la plus grande somme des valeurs pour se rendre du point de départ au sommet étudié. La lettre est le sommet précédent dans la chaîne (ou chemin) qui a cette plus grande somme. On identifie la chaîne (ou le chemin) par une lecture à rebours (à reculons). A 15 15 (A) B 5 20 (B) C 10 25 (B) 20 30 55 (D) G 30 60 (G) 5 H 15 95 (I) D 20 (A) E 30 50 50 75 (D) Chemin critique : ABDFIJK F 15 5 80 (F)15 J 0 95 (J) I Temps minimum pour réaliser le projet : 95 minutes K

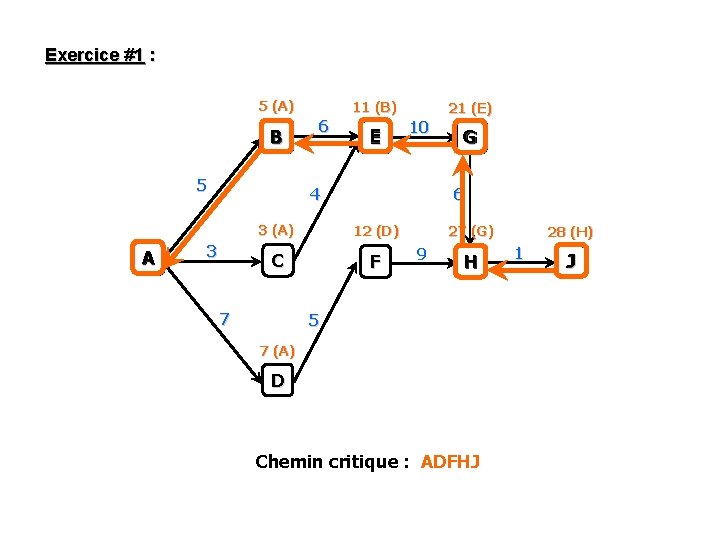
Exercice #1 : 5 (A) B 5 A 11 (B) 6 E 21 (E) 10 4 3 6 3 (A) 12 (D) C F 7 G G 27 (G) 9 H 5 7 (A) D Chemin critique : ADFHJ 28 (H) 1 J

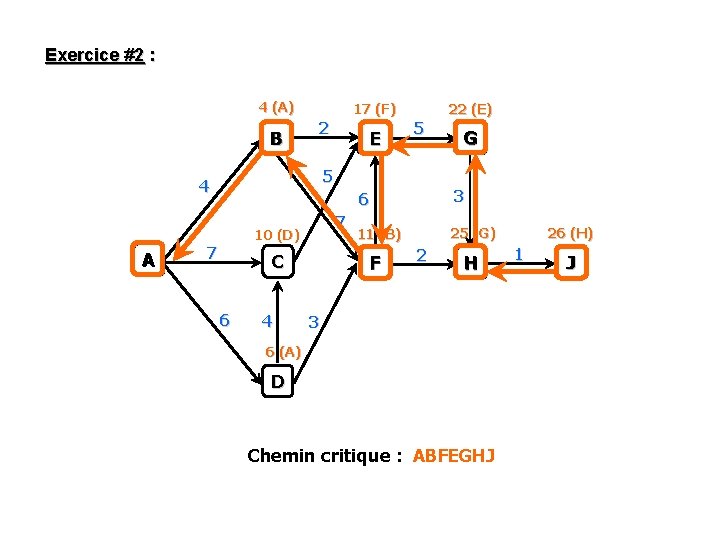
Exercice #2 : 4 (A) B 17 (F) 2 5 5 4 A E 22 (E) 7 10 (D) 7 C 6 4 G 6 3 11 (B) 25 (G) F 2 H 3 6 (A) D Chemin critique : ABFEGHJ 26 (H) 1 J