Packing to fewer dimensions for space compression and

Packing to fewer dimensions (for space compression and query speedup) Paolo Ferragina Dipartimento di Informatica Università di Pisa

Speeding up cosine computation n What if we could take our vectors and “pack” them into fewer dimensions (say 50, 000 100) while preserving distances? n n n Now, O(nm) to compute cos(d, q) for all n docs Then, O(km+kn) where k << n, m Two methods: n n Latent semantic indexing Random projection

Briefly n LSI is data-dependent n n Create a k-dim subspace by eliminating redundant axes Pull together “related” axes – hopefully n n car and automobile What about polysemy ? Random projection is data-independent n Choose a k-dim subspace that guarantees good stretching properties with high probability between any pair of points.

Sec. 18. 4 Latent Semantic Indexing courtesy of Susan Dumais

Notions from linear algebra n n n Matrix A, vector v Matrix transpose (At) Matrix product Rank Eigenvalues l and eigenvector v: Av = lv Example

Overview of LSI n Pre-process docs using a technique from linear algebra called Singular Value Decomposition n Create a new (smaller) vector space n Queries handled (faster) in this new space

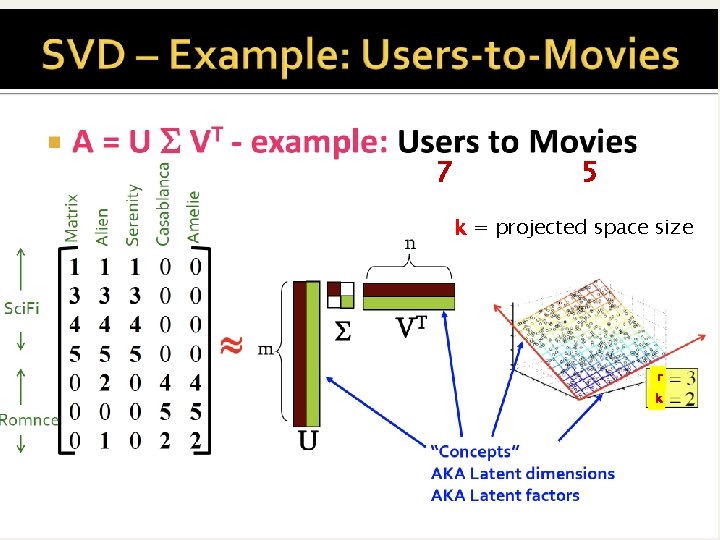
Singular-Value Decomposition n Recall m n matrix of terms docs, A. n A has rank r m, n Define term-term correlation matrix T=AAt n T is a square, symmetric m m matrix n Let U be m r matrix of r eigenvectors of T Define doc-doc correlation matrix D=At. A n D is a square, symmetric n n matrix n Let V be n r matrix of r eigenvectors of D

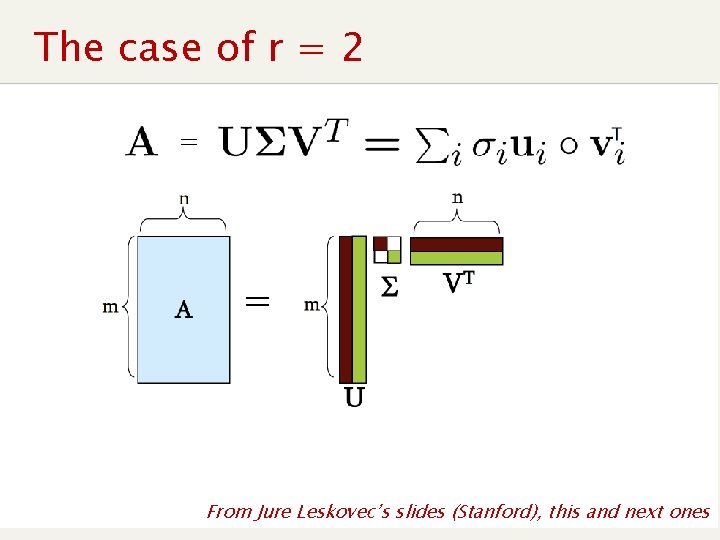
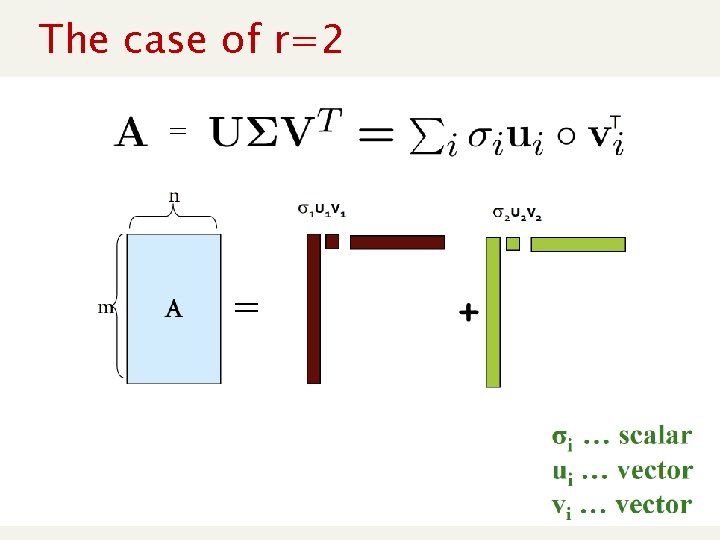
A’s decomposition n n Given U (for T, m r) and V (for D, n r) formed by orthonormal columns (unit dot-product) It turns out that A = U S Vt n Where S is a diagonal matrix with the singular values (=square root of the eigenvalues of T=AAt ) in decreasing order. m n A = m r U r r S r n Vt

The case of r = 2 = = From Jure Leskovec’s slides (Stanford), this and next ones

The case of r=2 = =

7 5 k = projected space size r k

r=3

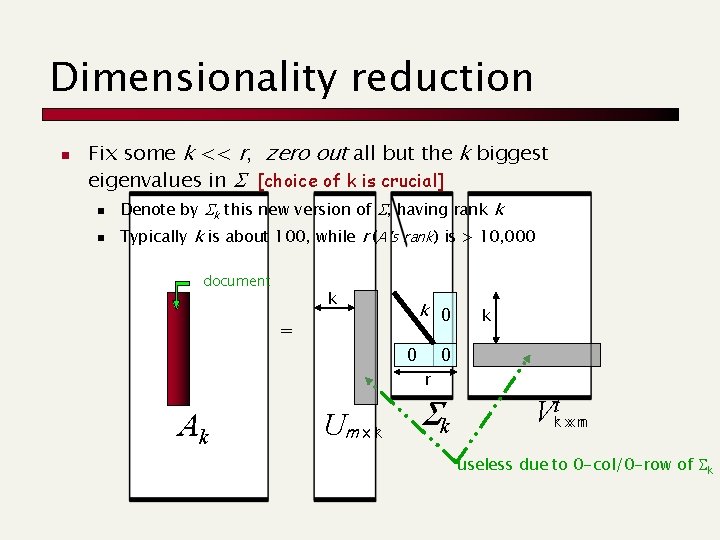
Dimensionality reduction n Fix some k << r, zero out all but the k biggest eigenvalues in S [choice of k is crucial] n n Denote by Sk this new version of S, having rank k Typically k is about 100, while r (A’s rank) is > 10, 000 document k k 0 = 0 k 0 r Ak Um x kr Sk Vkrt xx nn useless due to 0 -col/0 -row of Sk

Guarantee n Ak is a pretty good approximation to A: n n Relative distances are (approximately) preserved Of all m n matrices of rank k, Ak is the best approximation to A wrt the following measures: n min. B, rank(B)=k ||A-B||2 = ||A-Ak||2 = sk+1 n min. B, rank(B)=k ||A-B||F 2 = ||A-Ak||F 2 = sk+12+ sk+22+. . . + sr 2 n Frobenius norm ||A||F 2 = s 12+ s 22+. . . + sr 2

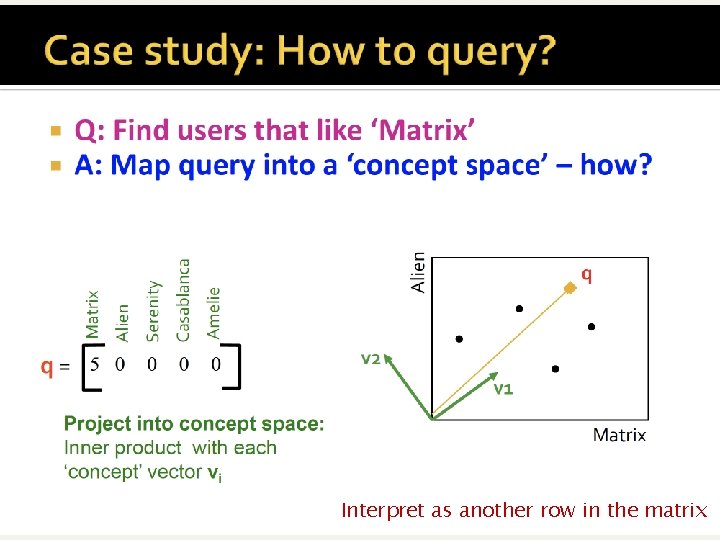
Interpret as another row in the matrix

This product U * S gives the projection of users to the 2 new dims, corresponding to the vectors v 1, v 2 of V matrix below

This is a new user that expresses preferences on-the-fly at query time d

Recap n c-th concept = c-th col of Uk n (which is m x k) Uk[i][c] = strength of association between c-th concept and i-th row (term/user/…) n Vtk[c][j] = strength of association between c-th concept and j-th column (document/movie/…) n n Projected query: q’ = q Vk n q’[c] = strenght of concept c in q Projected column (doc/movie): d’j = dj Vk n d’j [c] = strenght of concept c in dj