Compression Introduction Information theory Text compression IL compression

Compression דחיסה • Introduction • Information theory • Text compression • IL compression DL - 2004 Compression – Beeri/Feitelson 1

General: Compression methods depend on data characteristic there is no universal (best) method Requirements: • text, EL’s: lossless • images – may be lossy • efficiency -- how may bits per byte of data? (often in percentage) • coding should be fast, decoding superfast DL - 2004 Compression – Beeri/Feitelson 2

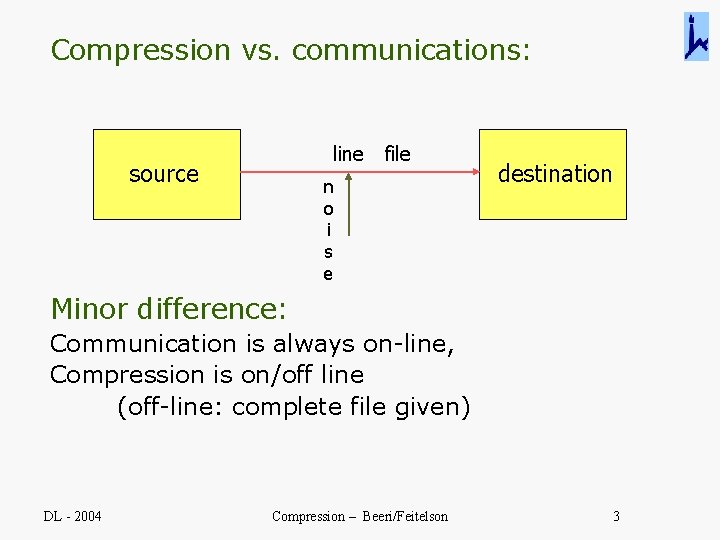
Compression vs. communications: line source file n o i s e destination Minor difference: Communication is always on-line, Compression is on/off line (off-line: complete file given) DL - 2004 Compression – Beeri/Feitelson 3

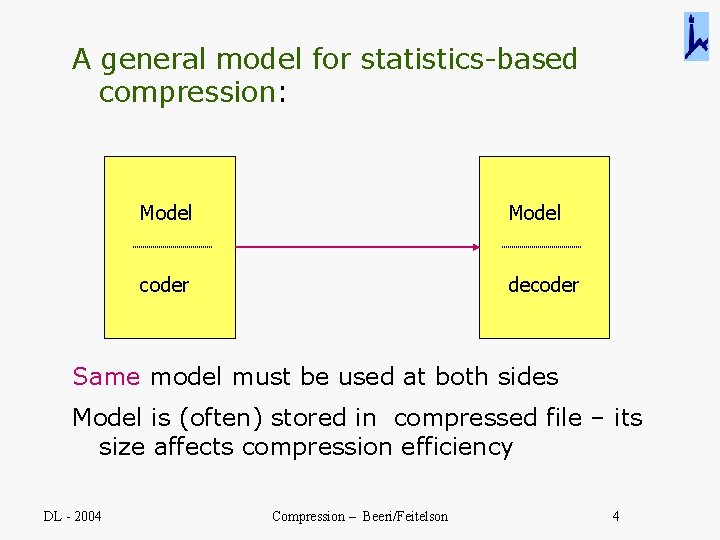
A general model for statistics-based compression: Model coder decoder Same model must be used at both sides Model is (often) stored in compressed file – its size affects compression efficiency DL - 2004 Compression – Beeri/Feitelson 4

Appetizer: Huffman coding (standard) binary coding: • Uniquely decodable • Model = table • efficiency: bits/symbol (no/little compression) Can do better if symbol frequencies are known: frequent symbol – short code rare symbol – long code Minimizes the average DL - 2004 Compression – Beeri/Feitelson 5

Assume: Huffman’s Algorithm (eager construction of code tree): • Allocate a node for each symbol, weight = symbol probability • Enter nodes into priority queue Q (small weights first) • While |Q|>1 { – Remove two first nodes (smallest weights) – Create new node, make it their parent, assign it the sum of their weights – Enter new node into Q } Return: single node in Q (root of tree) DL - 2004 Compression – Beeri/Feitelson 6

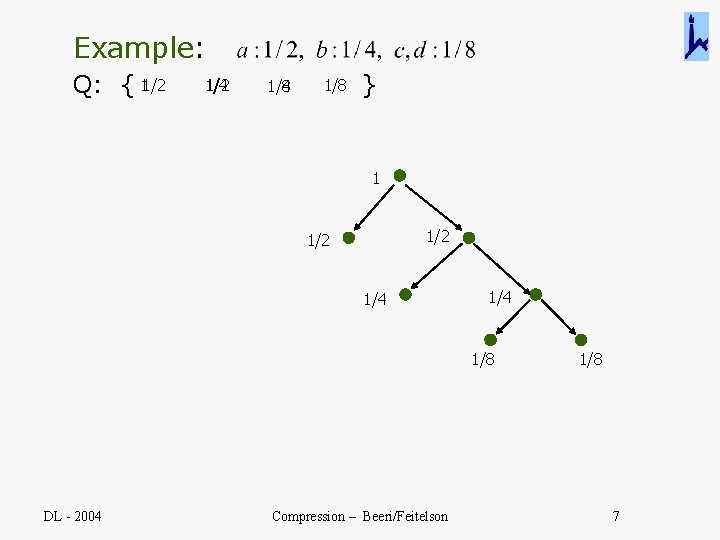
Example: Q: { 11/2 1/4 1/8 } 1 1/2 1/4 1/8 DL - 2004 Compression – Beeri/Feitelson 1/8 7

How are the trees used? Coding: for each symbol s, output binary path from root to leaf(s) Decoding: read incoming stream of bits, follow path from root of tree. When leaf(s) reached, output s, and return to root. Common model (stored on both sides) : the tree DL - 2004 Compression – Beeri/Feitelson 8

Expected cost bits/symbol: Binary: Huffman : In example: binary: 2 Huffman : 1/2 x 1 + ¼x 2 + 1/8 x 3 = 1. 75 Q: what would be the tree and cost for: 5/12, 1/3, 1/6, 1/12 ? DL - 2004 Compression – Beeri/Feitelson 9

A note on Huffman trees: The algorithm is non-deterministic: • In each step, either node can be the left child of new parent If two children of a node are exchanged, result is also a Huffman tree Closure under rotation w. r. t nodes • Consider 0. 4, 0. 2, 0. 1 after 1 st step, 2 out of 3 nodes are selected There are many Huffman trees for a given probability distribution DL - 2004 Compression – Beeri/Feitelson 10

Concepts: variable length code: (e. g. Huffman) uniquely decodable code: each legal code sequence is generated by a unique source sequence instantaneous/prefix code מיידי end of code of each symbol can be recognized Examples: 0, 01, 10 10, 00, 110, 111 (Huffman of example) (comma code) 0, 011, 111 (inverted comma code) DL - 2004 Compression – Beeri/Feitelson 11

A prefix code = binary tree Every binary tree with q leaves is a prefix code for q symbols, lengths of code words = lengths of paths Kraft inequality: Exists a q-leaf tree with path lengths iff =1 iff tree is complete DL - 2004 Compression – Beeri/Feitelson 12

Proof : assume exists a tree T Take T’ to be the full tree of depth The number of its leaves: A leaf of T, at distance from root leaves of T’ under it has T Sum on all leaves of T: Full: all paths same length DL - 2004 Compression – Beeri/Feitelson 13

If T is not complete (every node has 0/2 children) it has a node with a single child Can be “shortened” new tree still satisfies hence given tree must satisfy Only complete trees have equality Comment: In general a prefix code that is not a complete tree is dominated by a tree with smaller cost From now: tree are complete DL - 2004 Compression – Beeri/Feitelson 14

ç: Assume Lemma: if Replace these two by their sum (hence q-1 lengths) and use induction Assume DL - 2004 must the tree be complete? Compression – Beeri/Feitelson 15

Mac. Millan Theorem : exists a uniquely decodable code with lengths iff Corollary: when there is a uniquely decodeable code, there is also a prefix code (same cost) No need to think about the first class Uniquely decodable prefix DL - 2004 Compression – Beeri/Feitelson 16

On optimality of Huffman: Cost of a tree/code T: L(T) = Claim: if a tree T does not satisfy then it is dominated by a tree with smaller cost Claim: for any T, Proof: can assume T satisfies (*) Use induction: Q=2: both trees have lengths 1, 1 DL - 2004 Compression – Beeri/Feitelson 17

Q>1: In Huffman tree, there are two maximal paths that end in sibling nodes In T, the paths for last two symbols are longest (by (*)) but their ends may not be siblings But, T is complete, hence the leaf with has a sibling with same length; exchange with the leaf corresponding to Now, in both trees, these two longest paths can be replaced by their parents Case of q-1 (induction hypothesis) DL - 2004 Compression – Beeri/Feitelson 18

Summary: • Huffman trees are optimal hence satisfy (*) • Any two Huffman trees have equal costs • Huffman trees have min cost among all trees (codes) DL - 2004 Compression – Beeri/Feitelson 19