Speech Compression Speech Compression objectives Speech compression refers

Speech Compression

Speech Compression objectives Speech compression refers to the reduction of the amount of data required to represent the signal Speech compression is required for n n Reduction in storage requirements Speeding of speech transmission

Uncompressed Speech Signal The volume of data involved in speech signal is moderate. For an average quality of speech, a band of 4 k. Hz is sufficient. n A sampling rate of 8 k. Hz and quantization of 8 bits/sample entail a data rate of 64 kbits/sec A high quality of speech (and music) is provided with a band of 20 k. Hz. n A sampling rate of 44 KHz, and quantization with 12 bits/sample lead to a data rate of 528 Kbits/sec Only a few tens of thousands of bits can be sent each second through a telephone line. Thus, a second of moderate quality speech requires a second to go through a telephone line. A compact disc of 1 GB can store about 4 hours of uncompressed audio of high quality

Why Speech can be compressed A speech signal can be compressed because of n n n speech characteristics listener characteristics probabilistic considerations

Redundancy in Speech There is a correlation (dependency) between values of neighboring samples. In other words, most of the data in the signal is in the low frequency range, implying a gradual change of amplitude. This enables the estimation of a sample value, based on the values of neighboring samples. The speech signal is mostly limited to a range of 4 KHz. Thus, sampling rate of 8 KHz is mostly sufficient High frequencies may be eliminated, or represented with less accuracy (no. of bits)

Listener Characteristics The human auditory system is limited in its sensitivity to a range of 20 KHz. Thus, higher frequencies in the signal can be eliminated with no effect on the listener (for speech, even a lower limit can be applied) An important characteristic of the human auditory system is that an audio signal segment of high amplitude masks a neighboring segment of low amplitude, such that the second is not heard This characteristic enables a less detailed representation of the low amplitude segments

Probabilistic Considerations When different data values have different probability, an economic representation may be achieved, if the more probable values are represented with fewer bits (Statistical Coding) Repeating values can be coded based on their previous appearances (LZW)

Compression Characteristics Loss-less and lossy compression: n n In a loss-less compression methods the signal can be restored from its compressed form without any loss of information In a lossy compression methods a perfect restoration of the signal from its compressed form is not possible Lossy methods allow higher compression rates than the loss-less methods.

Compression Characteristics Compression Ratio is the ratio between the volume of data in the compressed and original (uncompressed) signal A compression ratio of upto 1: 10 is achievable with loss-less methods, and a ratio of 1: 100 and higher may be achieved with lossy methods The quality of the restored (from compression) signal can be measured n n Objectively as the mean-square error between the samples of the original and restored signals Subjectively, from the impression of listeners subjected to the original and restored signals

Common Compression Methods Raw-data reduction is generally not acceptable as a way to achieve a significant compression, since the quality of speech obtained is not acceptable The common compression methods are more complicated than a simple raw-data reduction, and they include n n n Sample coding, where each sample is coded separately, without reference to its neighbors Prediction coding, which uses the similarity of values of adjacent samples to predict a sample value based on its neighbors, thus reducing inter-sample redundancy Transform coding, which performs a mathematical transformation of the signal, producing a domain where the redundancy is more obvious and more easily removed

Statistical (Entropy) Coding The common uncompressed speech coding (PCM) represents each sample with the same number of bits. Allowing L amplitude values, each sample is log 2 L bits long. Statistical coding of signals assigns each value a different number of bits, according to the probability of its appearance. The more frequent values are assigned a smaller number of bits

Statistical Coding The number of bits assigned to level k in statistical coding is where pk is the probability of level k. The average number of bits for a sample is and the compression ratio is When all the L levels have the same probability (pk=1/L), there is no benefit in using statistical coding:

Statistical Coding When all samples are coded with the same number of bits, there is no problem in separating between successive samples in a stream. However, the separation problem does exist in statistical coding, when each sample may have a different length. For a possible separation between samples, the requirement is that no codeword is a prefix of another codeword. However, this requirement stands in contrast to the desire to obtain an efficient (short) code.

Statistical Coding The distribution of speech sample values is approximately uniform. Namely, the probability of all values is about the same (particularly when considering a long segment). Therefore, statistical coding is not efficient for speech signal in time. However, it is different in the frequency domain. There, the large values are at low frequencies, which are smaller in number. In contrast, the high frequency components, which are large in number, have low values. Statistical coding of speech is possible in frequency domain, where high frequencies, which are more frequent, are coded with a smaller no. of bits

Predictive Coding Commonly in speech signals, there is a high correlation among values of neighboring samples. This similarity of values represents redundancy in speech information – information that can be done without Predictive coding is design to reduce/ eliminate inter-sample redundancies
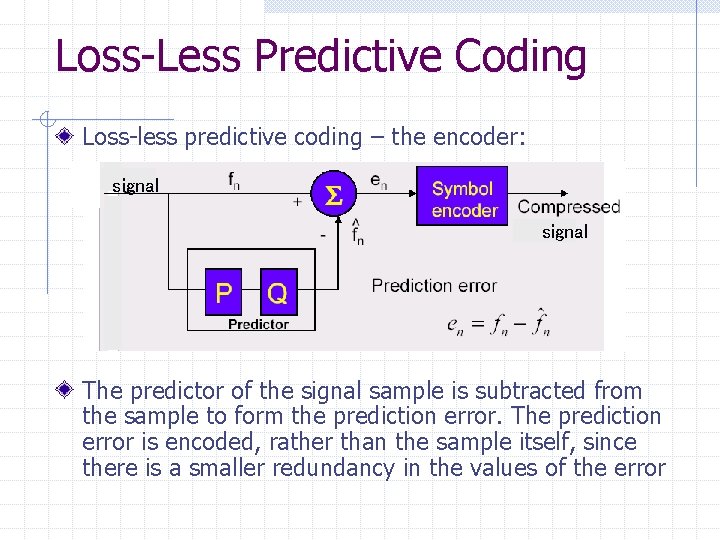
Loss-Less Predictive Coding Loss-less predictive coding – the encoder: signal The predictor of the signal sample is subtracted from the sample to form the prediction error. The prediction error is encoded, rather than the sample itself, since there is a smaller redundancy in the values of the error
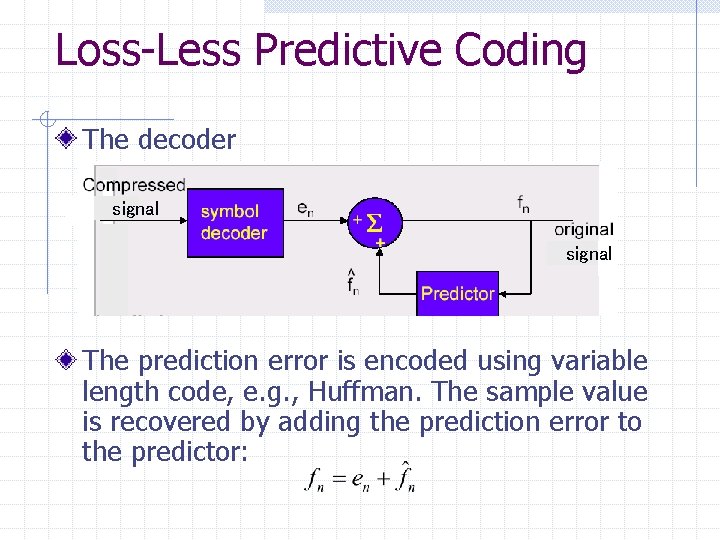
Loss-Less Predictive Coding The decoder signal The prediction error is encoded using variable length code, e. g. , Huffman. The sample value is recovered by adding the prediction error to the predictor:

A First Order Predictor An example of a first order predictor: as shown in the histograms, the range of the prediction error (the difference) is much smaller than that of the samples, so that fewer bits are needed for the representation Variable length coding can then be used to encode the difference, since smaller values are more probable
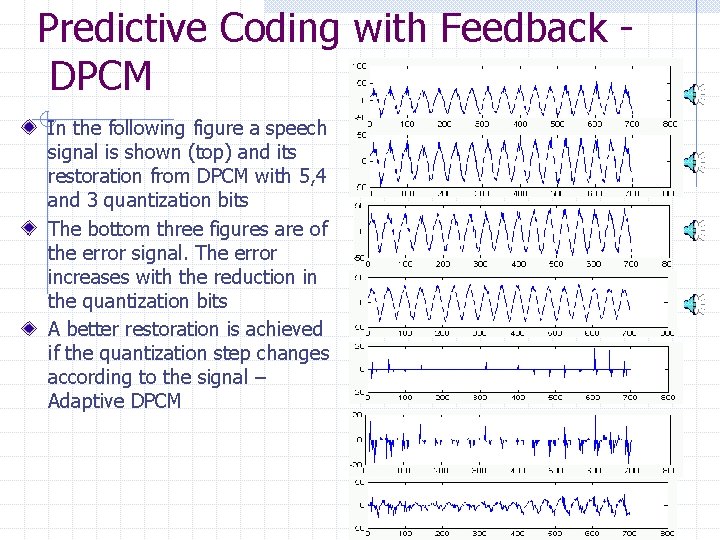
Predictive Coding with Feedback DPCM In the following figure a speech signal is shown (top) and its restoration from DPCM with 5, 4 and 3 quantization bits The bottom three figures are of the error signal. The error increases with the reduction in the quantization bits A better restoration is achieved if the quantization step changes according to the signal – Adaptive DPCM

Transform Coding Transform coding acts in the transform domain rather than time domain. The basic idea is that in the transform domain the distribution of values is more suitable for compression As mentioned, redundancy in time domain is due to intersample similarity. If the transform is to frequency domain, this redundancy is expressed in the concentration of most energy in a small number of coefficients, those corresponding to low frequencies. In addition, since the ear is not sensitive to high frequencies, the degradation, when only the low-frequency coefficients are considered, is not significant If the transform is one-to-one, the information in time domain and transform domain is identical, and no compression is obtained by simply changing the domain

Transform Coding The more common transform used for compression are : n n Fourier transform Cosine transform Karhunen-Loeve transform Wavelet transform The transform is performed on signal blocks: the signal is subdivided into small blocks, and each block is transformed separately. The division into blocks causes blocking artifacts: the boundaries between blocks are audible when the compressed signal is restored
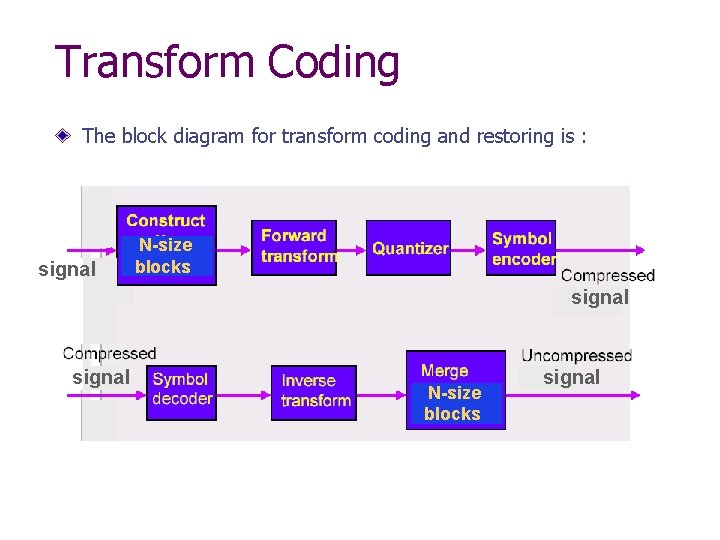
Transform Coding The block diagram for transform coding and restoring is : signal N-size blocks signal

Cosine Transform The most commonly used transform for compression is the Cosine transform. It is used rather than the similar Fourier transform, since it allows the concentration of information into a smaller number of coefficients Transform coding of a signal with Cosine transform, retaining only 25% of the coefficients, produces half the error than the Fourier transform does, in the restored uncompressed signal The expression for the 1 D Cosine transform of a sequence x(n) of length N is : The 1 D transform can be computed from the Fourier transform Y(k) of y(n) - a symmetrical extension of the sequence x(n): The expression for the 1 D Inverse Cosine transform :

Cosine Transform
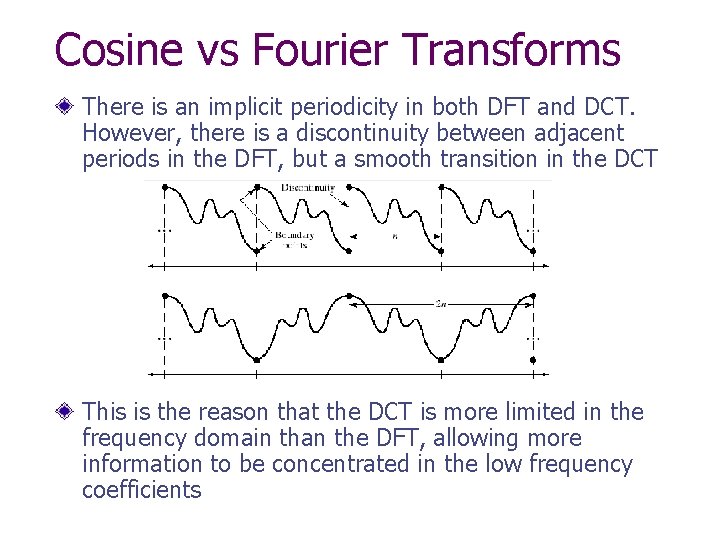
Cosine vs Fourier Transforms There is an implicit periodicity in both DFT and DCT. However, there is a discontinuity between adjacent periods in the DFT, but a smooth transition in the DCT This is the reason that the DCT is more limited in the frequency domain than the DFT, allowing more information to be concentrated in the low frequency coefficients

Block Quantization Compression in transform coding is achieved by an appropriate selection of transform coefficients, and quantizing the selected coefficients There are two ways to select the transform coefficients: n n Zonal selection Threshold selection With zonal selection, only the coefficients corresponding to low frequencies are selected for each block. In the DCT, this coefficients are located at the beginning of the transform block With threshold selection, the significant coefficients are selected, those with a large value. The location of these coefficients in each block may be different. Thus, in addition to their values, the locations of the selected coefficients are to be stored Rather than specifying the location of the selected coefficient, the number of zeros from the previous selected coefficient (unselected coefficients) may be specified

Bit Allocation Bit allocation for the selected coefficients may n n n Be the same for all coefficients Vary with the location (lower frequencies – more bits assigned) Vary with the variance of the coefficients In the first case the compression ratio is n/N, where N is the number of samples in a block, and n is the number of selected coefficients In the second case, bit allocation may decreased gradually with the increase in frequency After bit allocation, the coefficients are ordered in a sequence

Signal Reconstruction from Compression Reconstruction of the signal from its compressed form is done by n decoding the transform coefficients n rearranging the coefficients in blocks (including zeros for unused coefficients) n performing the inverse transform on each block and n attaching the blocks together

Transform Coding - Example The figure shows a segment of a speech signal (top) and its restoration after transform coding (zonal selection) with compression ratio of 2, 4 and 8 (top to bottom) The larger the number of bits/sample used (the lower the compression ratio), the higher is the resemblance of the restored signal to the original

Transform Coding on the DSK The transform coding implemented is of zonal selection a block of N signal samples is DCT transformed, and the first n samples in the transform domain (corresponding to low frequencies) are selected (the other transform samples are zeroed). This entails a compression ratio of N/n Reconstruction of the signal is done a block at a time – the block of the transform samples (including the zero samples) is inverse transformed

Transform Coding on the DSK The code for the transform coding is very similar to that used in the FFT-IFFT program on the DSK, except that the a DCT and IDCT functions are used instead After the DCT of a block is calculated, and some of the transform samples zeroed, the inverse DCT is applied, forming the reconstructed block. The DCT and IDCT functions used are A direct slow calculations of transform equations A fast DCT and IDCT using FFT Both versions use a pre-calculated table of the cosine values used in the transform

Real-Time DCT Computation The actual code for the calculation of DCT in real-time is as follows: //TRAN_CODE. c implementation calling a C-coded DCT and IDCT functions #include <math. h> #define PTS 32 #define PI 3. 14159265358979 #define N 8 // # of points for DCT //No. of selected coefficients void DCT(float *Y, int N); //FFT prototype float iobuffer[PTS]; //as input and output buffer float x 1[PTS]; //intermediate buffer short I, k, n; //general purpose index variable short buffercount = 0; //number of new samples in iobuffer short flag = 0; //set to 1 by ISR when iobuffer full float w[PTS]; //twiddle constants stored in w float samples[PTS]; //primary working buffer main() { for (k = 0 ; k<PTS ; k++) //set up twiddle constants in w for (n=0 ; n<PTS ; n++) w[n][k] = cos(PI*(2*n+1)*k/(2*PTS)) ; //twiddle constants comm_intr(); //init DSK, codec, Mc. BSP

Real-Time DCT Computation The code continued : while(1) //infinite loop { while (flag == 0) ; //wait until iobuffer is full flag = 0; //reset flag for (i = 0 ; i < PTS ; i++) //swap buffers { samples[i]=iobuffer[i]; //buffer with new data iobuffer[i] = x 1[i]; //processed frame to iobuffer } DCT(samples, PTS); //call function DCT. c for (i = N ; i < PTS ; i++) samples[i] = 0 ; //Zero selected transform samples IDCT(samples, PTS); for (i = 0 ; i < PTS ; i++) x 1[i]=samples[i] ; } } //end of main //call function IDCT. c //intermediate buffer //end of infinite loop
![Real-Time DCT Computation The sampling ISR : interrupt void c_int 11() //ISR { output_sample((int)(iobuffer[buffercount])); Real-Time DCT Computation The sampling ISR : interrupt void c_int 11() //ISR { output_sample((int)(iobuffer[buffercount]));](http://slidetodoc.com/presentation_image_h/0a64166ad0818cfd5105cf0b366d2740/image-34.jpg)
Real-Time DCT Computation The sampling ISR : interrupt void c_int 11() //ISR { output_sample((int)(iobuffer[buffercount])); //out from iobuffer[buffercount++]=(float)(input_sample()); //input to iobuffer if (buffercount >= PTS) //if iobuffer full { buffercount = 0; //reinit buffercount flag = 1; //set flag } }

Real-Time DCT Computation • The function used for the direct cosine transform, /* DCT. c - direct DCT */ void DCT(float *x, int N) { int k, n; float X[PTS] ; for (k=0; k<N; k++) { X[k]=0 ; for (n=0 ; n<N ; n++) X[k]=X[k]+2*x[n]*w[n][k] ; } for (k=0; k<N; k++) x[k]=X[k] ; }
- Slides: 35