Online Learning in Complex Environments Aditya Gopalan ece

Online Learning in Complex Environments Aditya Gopalan (ece @ iisc) MLSIG, 30 March 2015 (joint work with Shie Mannor, Yishay Mansour)

Machine Learning Algorithms/systems for learning to “do stuff” … … with data/observations of some sort. - R. E. Schapire Learning by Experience = Reinforcement Learning (RL) – (Action 1, Reward 1), (Action 2, Reward 2), … – Act based on past data, future data/rewards depend on present action; maximize some notion of utility / reward – Data interactively gathered

(Simple) Multi-Armed Bandit 1 2 3 … N “arms” or actions (items in a recommender system, transmission freqs, trades, …) each arm is an unknown probability distribution with parameter and mean (think Bernoulli)

(Simple) Multi-Armed Bandit Time 1 1 2 3 … N Play arm, collect iid “reward” (ad clicks, data rate, profit, …)

(Simple) Multi-Armed Bandit Time 2 1 2 3 … N

(Simple) Multi-Armed Bandit Time 3 1 2 3 … N

(Simple) Multi-Armed Bandit Time 4 1 2 3 … N

(Simple) Multi-Armed Bandit Time 1 2 Play awhile … 3 … N

Performance Metrics • Total (expected) reward at time • Regret: • Probability of identifying the best arm • Risk aversion: (Mean – Variance) of reward …

Motivation, Applications • • • • Clinical trials (original) Internet Advertising A/B testing Comment Scoring Cognitive Radio Dynamic Pricing Sequential Investment Noisy Function Optimization Adaptive Routing/Congestion Control Job Scheduling Bidding in auctions Crowdsourcing Learning in games

Upper Confidence Bound algo [Auer. Et. Al’ 02] Idea 1: Consider variance of estimates! Idea 2: Be optimistic under uncertainty! 1 2 Play arm maximizing 3 … N

UCB Performance [Auer. Et. Al’ 02] After plays, UCB’s expected reward is Per-round regret vanishes as t becomes large Learning

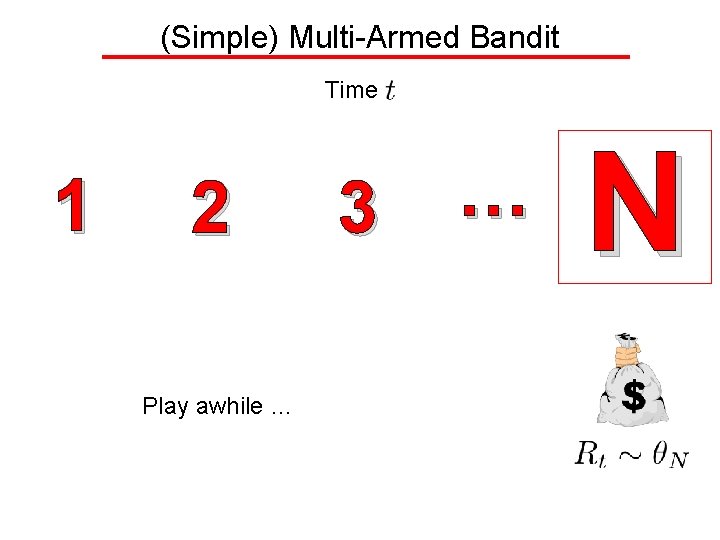
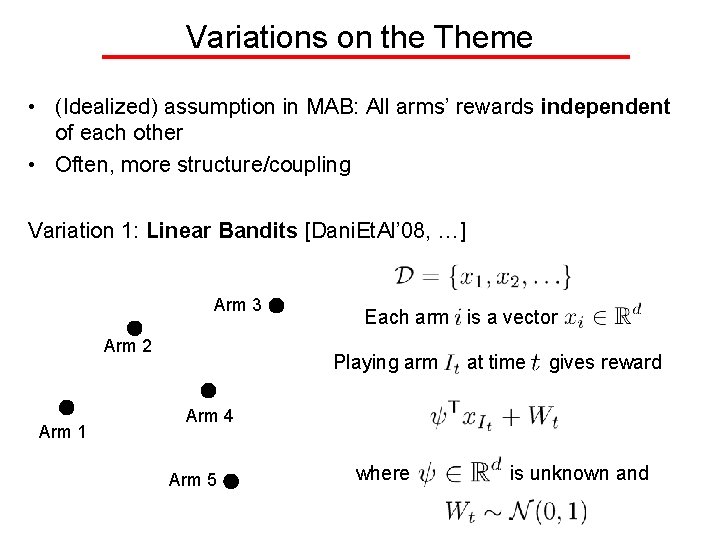
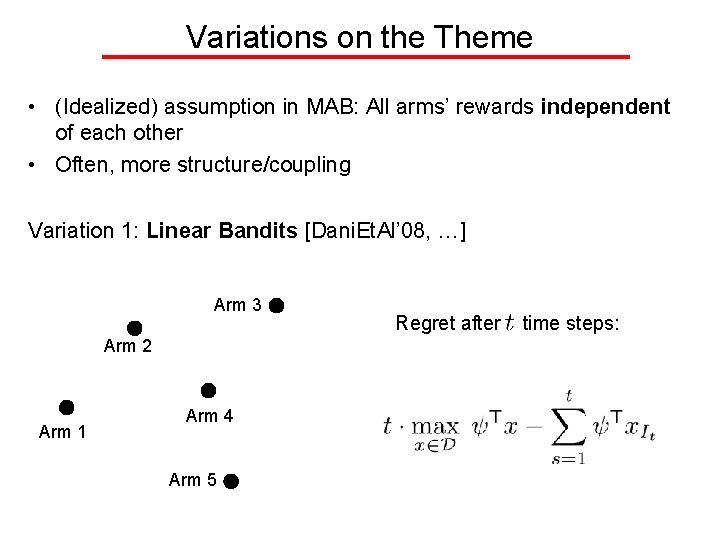
Variations on the Theme • (Idealized) assumption in MAB: All arms’ rewards independent of each other • Often, more structure/coupling Variation 1: Linear Bandits [Dani. Et. Al’ 08, …] Arm 3 Arm 2 Arm 1 Each arm is a vector Playing arm at time gives reward Arm 4 Arm 5 where is unknown and

Variations on the Theme • (Idealized) assumption in MAB: All arms’ rewards independent of each other • Often, more structure/coupling Variation 1: Linear Bandits [Dani. Et. Al’ 08, …] Arm 3 Arm 2 Arm 1 Arm 4 Arm 5 Regret after time steps:

Variations on the Theme • (Idealized) assumption in MAB: All arms’ rewards independent of each other • Often, more structure/coupling Variation 1: Linear Bandits [Dani. Et. Al’ 08, …] Arm 3 Arm 2 Arm 1 Arm 4 Arm 5 e. g. Binary vectors representing • Paths in a graph • Collection of subsets of a ground set (budgeted ad display) representing • Per edge/per element cost/utility

Variations on the Theme • (Idealized) assumption in MAB: All arms’ distributions/parameters independent/separate of each other • Often, more structure/coupling Variation 1: Linear Bandits [Dani. Et. Al’ 08, …] The Lin. UCB algo • Build a point estimate (least squares estimate) and a confidence region (ellipsoid) • Play the most optimistic action w. r. t. this ellipsoid,

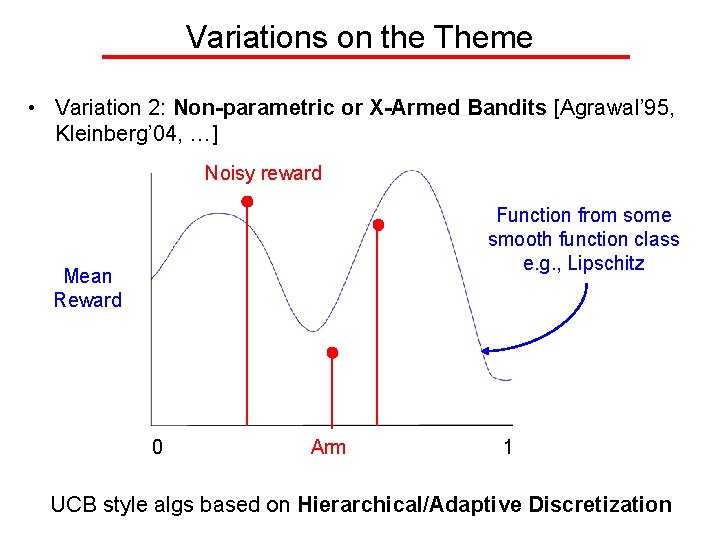
Variations on the Theme • Variation 2: Non-parametric or X-Armed Bandits [Agrawal’ 95, Kleinberg’ 04, …] Noisy reward Function from some smooth function class e. g. , Lipschitz Mean Reward 0 Arm 1 UCB style algs based on Hierarchical/Adaptive Discretization

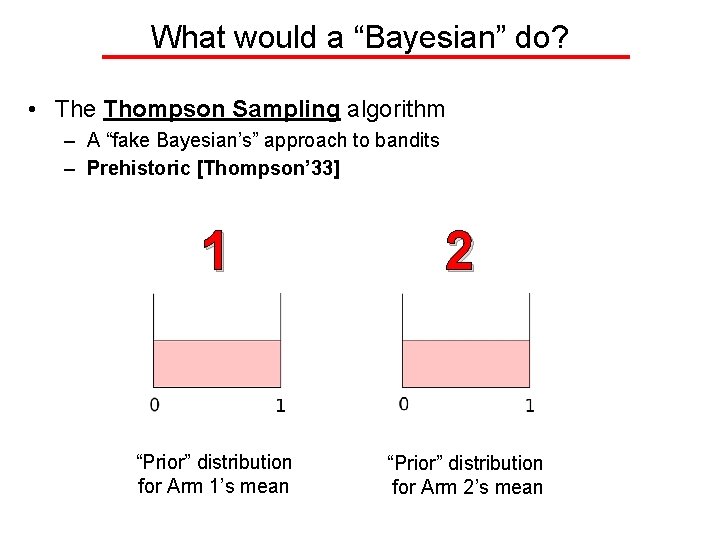
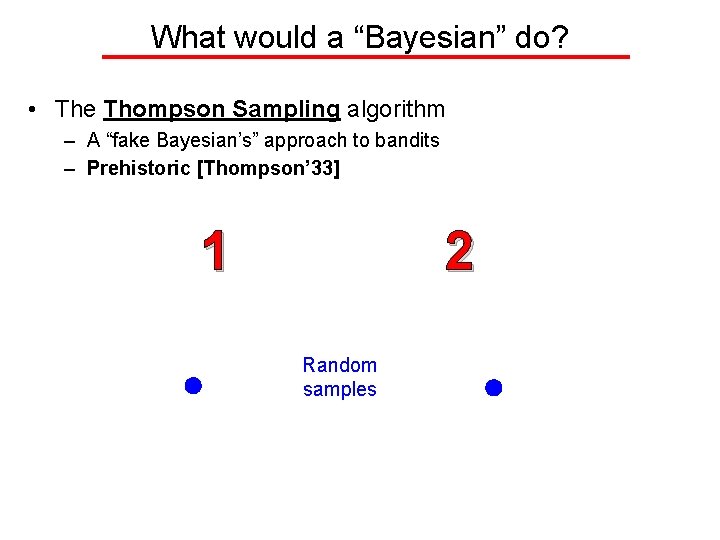
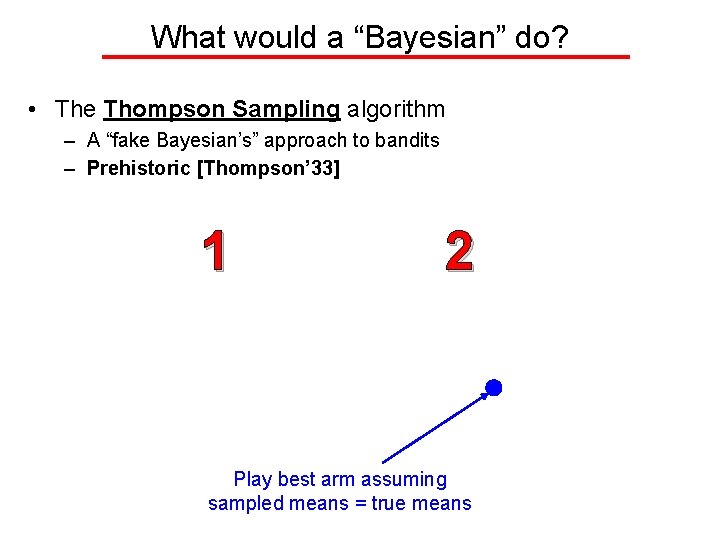
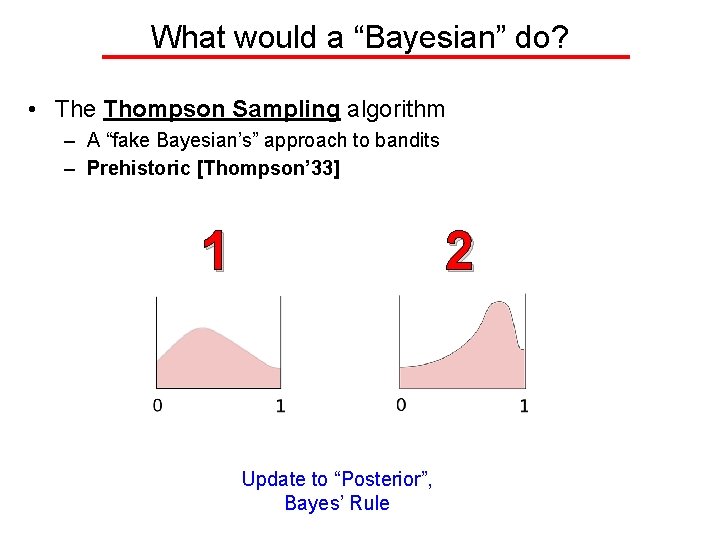
What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 “Prior” distribution for Arm 1’s mean “Prior” distribution for Arm 2’s mean

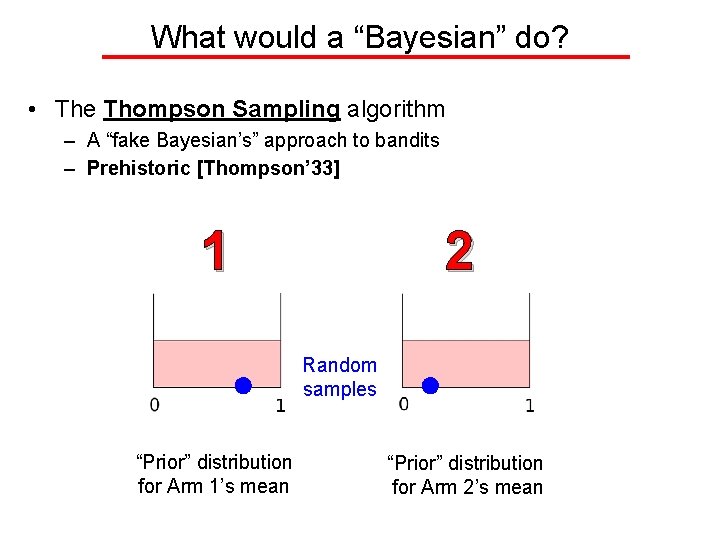
What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Random samples “Prior” distribution for Arm 1’s mean “Prior” distribution for Arm 2’s mean

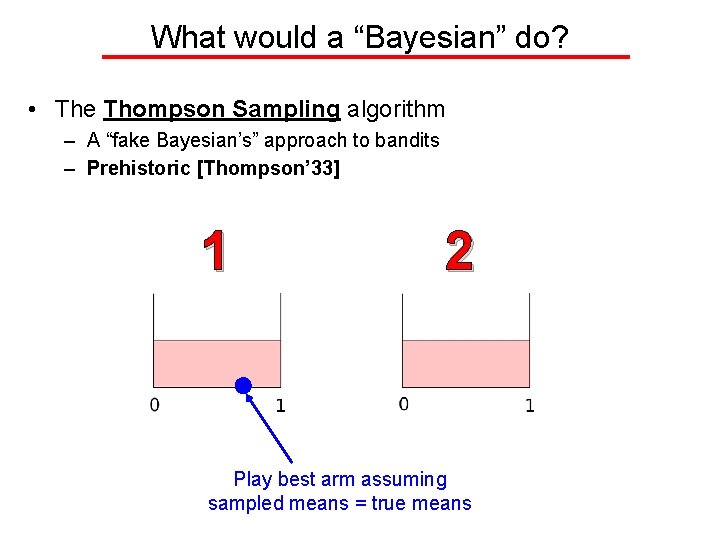
What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Play best arm assuming sampled means = true means

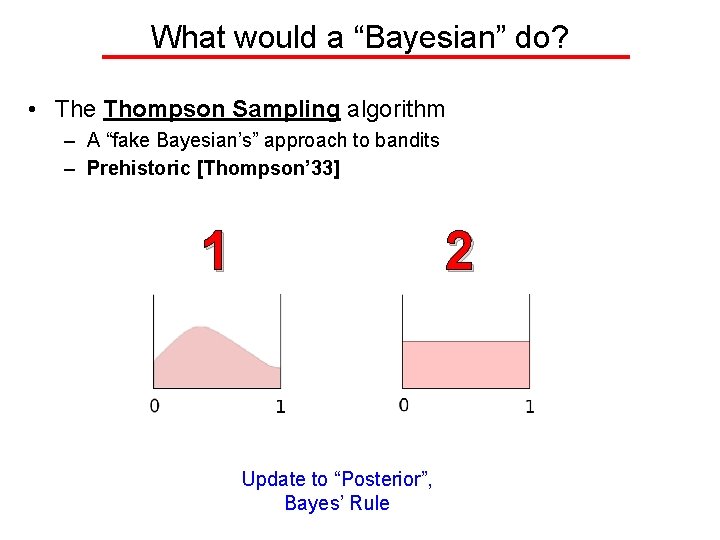
What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Update to “Posterior”, Bayes’ Rule

What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Random samples

What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Play best arm assuming sampled means = true means

What would a “Bayesian” do? • The Thompson Sampling algorithm – A “fake Bayesian’s” approach to bandits – Prehistoric [Thompson’ 33] 1 2 Update to “Posterior”, Bayes’ Rule

What we know • [Thompson 1933], [Ortega-Braun 2010] • [Agr-Goy 2011, 2012] – Optimal for standard MAB – Linear contextual bandits • [Kaufmann et al. 2012, 2013] – Standard MAB optimality • Purely Bayesian setting – Bayesian regret – [Russo-Van. Roy 2013] – [Bubeck-Liu 2013] • But analysis doesn’t generalize – Specific conjugate priors, – No closed-form for complex bandit feedback e. g. MAX

TS for Linear Bandits Idea: Use same Least Squares estimate as Lin-UCB, but sample from (multivariate Gaussian) posterior and act greedily! (no need to optimize over an ellipsoid) Shipra Agrawal, Navin Goyal. Thompson Sampling for Contextual Bandits with Linear Payoffs. ICML 2013.

More Generally – “Complex Bandits” 1 2 3 … N

e. g. Subset Selection

e. g. Job Scheduling

e. g. Ranking

General Thompson Sampling Imagine ‘fictitious’ prior distribution over all parameters

General Thompson Sampling Sample a set of parameters Prior

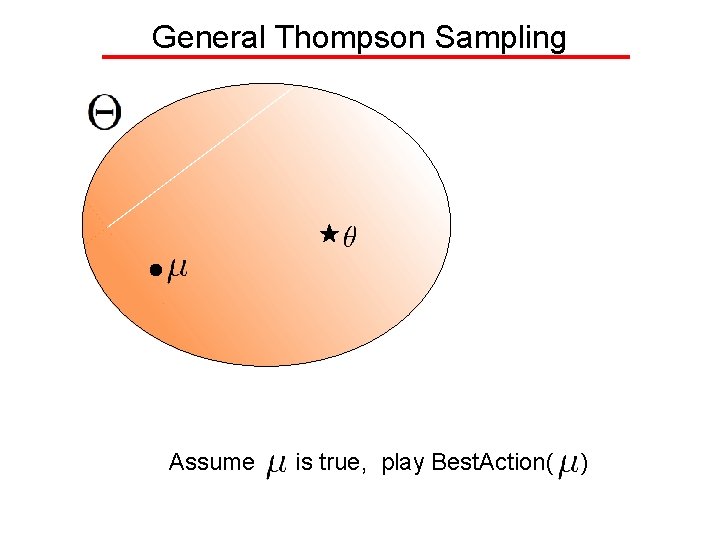
General Thompson Sampling Assume is true, play Best. Action( )

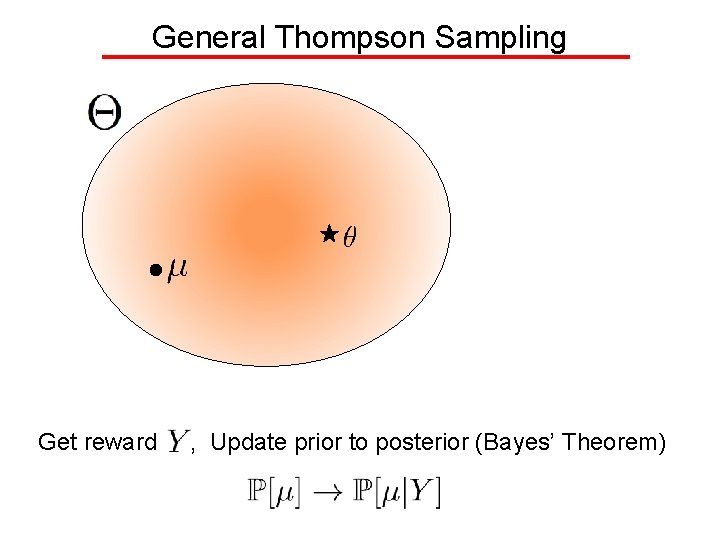
General Thompson Sampling Get reward , Update prior to posterior (Bayes’ Theorem)

Thompson Sampling Alg • = Space of all basic parameters • A fictitious prior measure – E. g. , = Uniform( ) • At each time – SAMPLE by current prior: – PLAY best complex action given sample: – GET reward: – UPDATE prior to posterior:

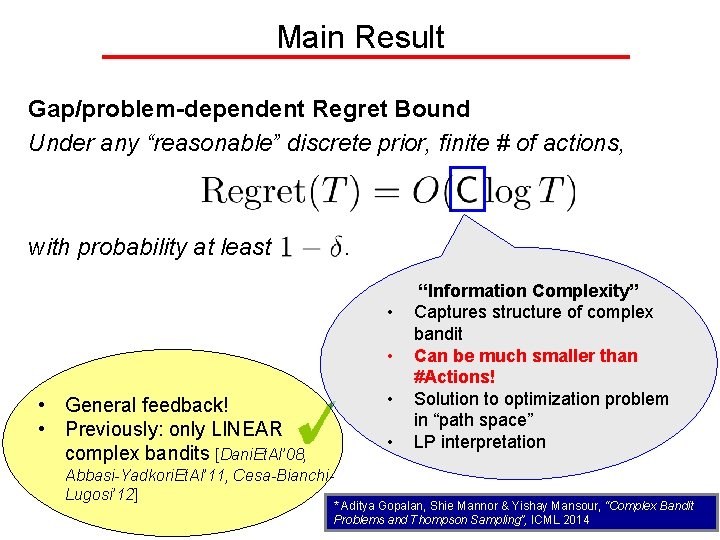
Main Result Gap/problem-dependent Regret Bound Under any “reasonable” discrete prior, finite # of actions, with probability at least . • • General feedback! • Previously: only LINEAR complex bandits [Dani. Et. Al’ 08, • Abbasi-Yadkori. Et. Al’ 11, Cesa-Bianchi. Lugosi’ 12] “Information Complexity” Captures structure of complex bandit Can be much smaller than #Actions! Solution to optimization problem in “path space” LP interpretation * Aditya Gopalan, Shie Mannor & Yishay Mansour, “Complex Bandit Problems and Thompson Sampling”, ICML 2014

Example 1: “Semi-bandit” Pick size-K subsets of arms, Observe All K chosen rewards “Semi-bandit” Regret Bound Under a reasonable prior, with probability at least , actions but regret only

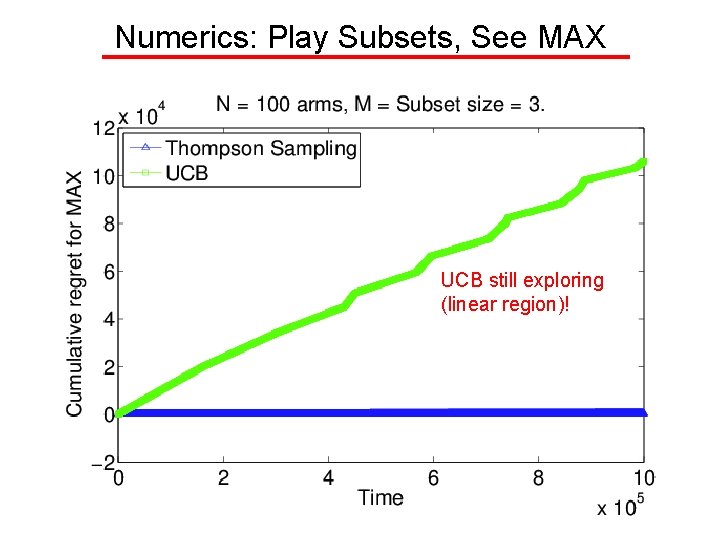
Example 2: MAX Feedback Pick size-K subsets of arms, Observe MAX of K chosen rewards Regret Bound under Max Feedback Structure Under a reasonable prior, with probability at least , SAVING! BOUND #ACTIONS

Numerics: Play Subsets, See MAX UCB still exploring (linear region)!

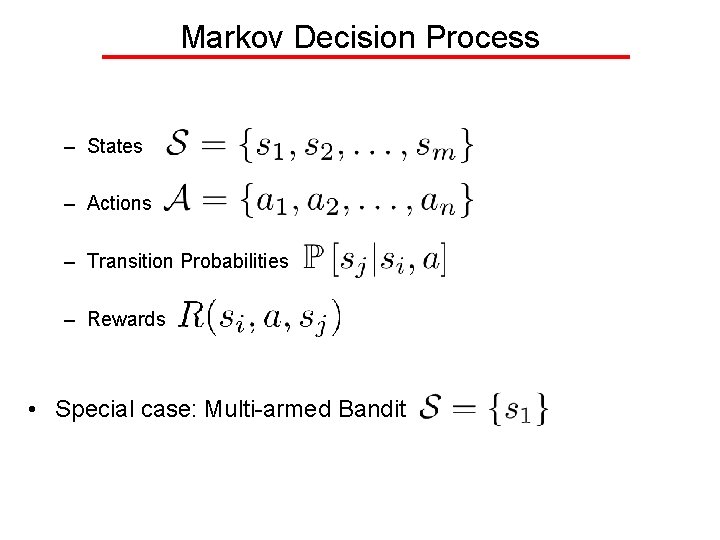
Markov Decision Process – States – Actions – Transition Probabilities – Rewards • Special case: Multi-armed Bandit

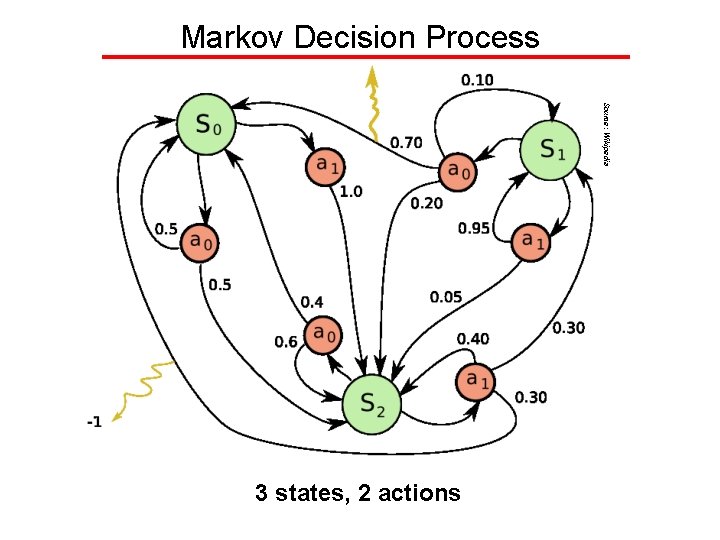
Markov Decision Process Source: Wikipedia 3 states, 2 actions

Online Reinforcement Learning • Suppose true MDP parameter is the decision maker a priori. , but this is unknown to • Must “LEARN optimal policy” - what action to take in each state to maximize equivalently, minimize regret

Online Reinforcement Learning • Tradeoff: Explore the state space or Exploit existing knowledge to design good current policy? • Upper Confidence-based approaches: Build confidence intervals per state-action pair, be optimistic! – Rmax [Brafman-Tennenholtz 2001] – UCRL 2 [Jaksch. Et. Al 2007] • Key Idea: Maintain estimates + high-confidence sets for transition probability & reward for every (state, action) pair • “Wasteful” if transitions/rewards have structure/relations

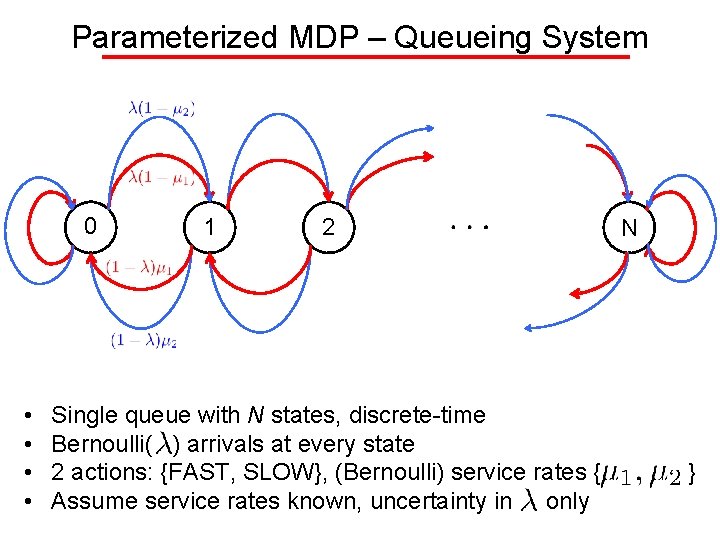
Parameterized MDP – Queueing System 0 • • 1 2 Single queue with N states, discrete-time Bernoulli( ) arrivals at every state 2 actions: {FAST, SLOW}, (Bernoulli) service rates { Assume service rates known, uncertainty in only N }

Thompson Sampling 1. Draw an MDP instance ~ Prior over possible MDPs 2. Compute optimal policy for instance (Value Iteration, Linear Programming, simulation, …) 3. Play action prescribed by optimal policy for current state Repeat indefinitely. In fact, consider the following variant (TSMDP): • Designate a marker state • Divide time into visits to marker state (epochs) • At each epoch 1. 2. 3. 4. Sample an MDP ~ Curent posterior Compute optimal policy for sampled MDP Play policy until end of epoch Update posterior using epoch samples

Numerics –Queueing System

Main Result [G. -Mannor’ 15] Under suitably “nice” prior on , with probability at least (1 - ), TSMDP gives regret B + C log(T) in T rounds, where B depends on , depends only on , the true model the “effective dimension” of. and the prior, C and, more importantly, • Implication: Provably rapid learning if effective dimensionality of MDP is small, e. g. , queueing system with single scalar uncertain parameter

Future Directions • Continuum-armed bandits? • Risk-averse decision making • Misspecified models (e. g. , “almost-linear bandits”) • Relax epoch structure? Relax ergodicity assumptions? • Infinite State/Action Spaces • Function Approximation for State/Policy Representations?

Thank you