OD DYFUZJI NORMALNEJ DO DYFUZJI ANOMALNEJ 100 lat























![Natrolite (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) Mineralny Natrolite (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) Mineralny](https://slidetodoc.com/presentation_image_h2/a0d04246a1ef1c05c6ae994ae382f181/image-33.jpg)

![Natrolit (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) M. Natrolit (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) M.](https://slidetodoc.com/presentation_image_h2/a0d04246a1ef1c05c6ae994ae382f181/image-35.jpg)







- Slides: 43

OD DYFUZJI „NORMALNEJ” DO DYFUZJI „ANOMALNEJ” (100 lat artykułu A. Einsteina i 150 lat artykułu A. Ficka ) Mikołaj Siergiejew Zakład Fizyki Ciała Stałego Instytut Fizyki US

Równanie dyfuzji (1855)

Równanie dyfuzji Ficka Równanie dyfuzji (II) Ficka wynika z równania ciągłości (prawa zachowania cząstek) oraz ze wzoru określającego strumień dyfuzyjny

A. Einstein. Ann. Phys. (Leipzig)14 (1905) 549 „O ruchu cząstek zawieszonych w nieruchomej cieczy zgodnym z teorią molekularno-kinetyczną ciepła”

Założenia A. Einsteina 1. Ruch Browna makrocząstki jest spowodowany częstymi uderzeniami ze strony znacznie mniejszych, szybko poruszających się molekuł cieczy. 2. Ruch molekuł cieczy jest chaotycznym a ich zderzenia z cząstką Browna możemy opisać tylko statystycznie zakładając, że zderzenia są częste i niezależne. W fizyce do A. Einsteina statystyka już była stosowana w pracach Maxwella oraz Boltzmanna do opisu możliwych równowagowych rozkładów. A. Einstein jednym z pierwszych (po Rayleigh’u - 1891) zastosował statystykę do opisu czasowej ewolucji układu a więc można uważać , że właśnie z pracy A. Einsteina od 1905 roku w fizyce zaczyna się rozwój dynamiki statystycznej.

Wyprowadzenie równania dyfuzji Niech P(x, t) jest gęstością prawdopodobieństwa znalezienia cząstki Browna w chwili t w punkcie x. Einstein (1905) założył, że rozkład cząstek w chwili t + określa równanie (1) Równanie (1) zakłada, że prawdopodobieństwo znalezienia cząstki w chwili t + w punkcie x jest suma (całka) iloczynów : prawdopodobieństwo znalezienia cząstki w chwili t w x - razy prawdopodobieństwo przejścia cząstki ( ) za czas z x - do x. To założenie jest wiadomo dziś jako określenie procesu Markowa (prof. A. A. Markov - Kazań – 1906) , a równanie (1) - podstawowe równanie ruchu dla wszystkich dynamicznych procesów Markowa, nazywa się obecnie równaniem Chapmana - Kolmogorowa (1931).

Wyprowadzenie równania dyfuzji Dla małych i możemy zapisać (2) (3) Obecnie rozwinięcia (2) i (3) stosowane w fizyce procesów Markowa noszą nazwę rozwinięć Kramersa (1940) – Moyal’ego (1949). Po podstawieniu (2) i (3) do równania (1) otrzymujemy

Wyprowadzenie równania dyfuzji Korzystając z założenia dyfuzji ( ) = (- ) otrzymujemy równanie (4) gdzie Równanie (4) jest szczególnym przypadkiem równania procesów losowych, które obecnie nosi nazwę równania Fokkera (1915) – Plancka (1917).

Rozkład Gaussa Rozwiązanie równania (4) ma postać (5) gdzie wariancja Ze wzoru (5) wynika, że średnie przemieszczenie cząstki Browna (pierwiastek z wariancji rozkładu Gaussa) wynosi (6)

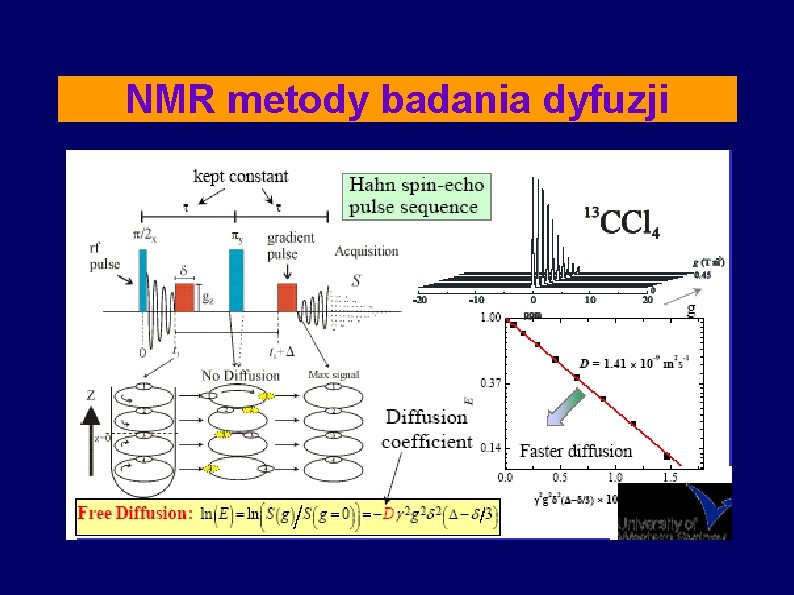
NMR metody badania dyfuzji

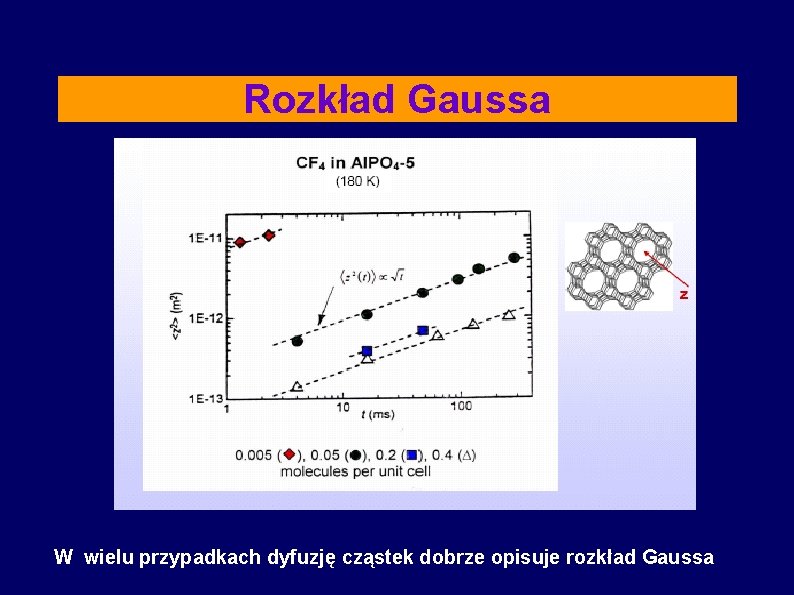
Rozkład Gaussa W wielu przypadkach dyfuzję cząstek dobrze opisuje rozkład Gaussa

Rozkłady Lévy’ego Rozkład Gaussa jest wyjątkowym rozkładem w statystyce – każdy rozkład o skończonej wariancji <x 2> (np. dwumianowy, Poissona i inne) dąży do rozkładu Gaussa ( centralne twierdzenie graniczne ). A zatem rozkład Gaussa jest atraktorem dla wielu innych rozkładów o skończonej wariancji. W 1926 roku francuski matematyk Paul Lévy udowodnił, że oprócz rozkładu Gaussa atraktorami mogą być inne rozkłady dla których jednak wariancja <x 2> = . Przykładem rozkładu Lévy’ego jest rozkład Cauchy’ego – Lorentza dla którego

Rozkłady Lévy’ego Rozkład Gaussa ma skończoną wariancję, a zatem gdy x rozkład Gaussa zanika jako Rozkłady Lévy’ego (Pareto) zanikają jako gdzie

Rozkłady Lévy’ego a Natura Pytanie: Czy istnieją w przyrodzie zjawiska które opisują rozkłady Lévy’ego ? Być może rozkład Lévy’ego jest tylko abstrakcją matematyczną ? Zaczynając od prac Benoita Mandelbrota (1963), udowodniono, że na co dzień spotykamy się dość często ze zjawiskami które opisują rozkłady Lévy’ego. Przykładami takich zjawisk są: fluktuacje cen akcji na gildie, fluktuacji rytmu serca, sposoby poszukiwania czegoś ( pożywienia, pracy, rozwiązania zagadnienia itd. ). Okazało się też, że istnieje dyfuzja którą opisuje nie rozkład Gaussa a rozkład Lévy’ego – anomalna albo fraktalna dyfuzja.

Rozkłady Lévy’ego (poszukiwanie pożywienia. . )

Swinney i inne (1993) Grupa Swinneya badała ciecz w wirującym pierścieniu. Wskutek turbulencji w różnych miejscach cieczy powstawały wiry. Śledzono za ruchem wrzuconej w ciecz makroskopowej cząstki. Obserwowana cząstka przez jakiś czas pozostawała w wirze a potem wykonywała „przelot” do drugiego wiru. Okazało się, że odstępy czasu między kolejnymi przelotami podlegają rozkładowi Lévy’ego o = 1. 3

Oliwiera i Penna (1995) Paulo Murilo i Thadeu Penna badali doświadczalno cieknący kran. Okazało się, że odstęp czasu między tworzeniem się kropli mają rozkład Lévy’ego, przy czym znajduje się w granicach 1. 66 – 1. 85. Interesującym jest to, że odstępy czasu między uderzeniami serca człowieka też opisuje rozkład Lévy’ego, przy czym u zdrowych osobników = 1. 7, podczas gdy u chorych pacjentów z ciężką niewydolnością serca 2 (rozkład Gaussa).

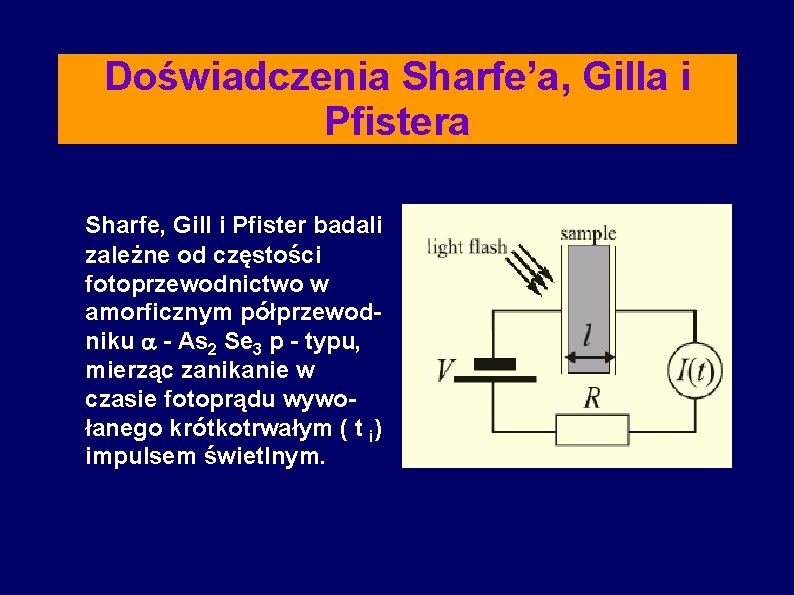
Doświadczenia Sharfe’a, Gilla i Pfistera Sharfe, Gill i Pfister badali zależne od częstości fotoprzewodnictwo w amorficznym półprzewodniku - As 2 Se 3 p - typu, mierząc zanikanie w czasie fotoprądu wywołanego krótkotrwałym ( t i) impulsem świetlnym.

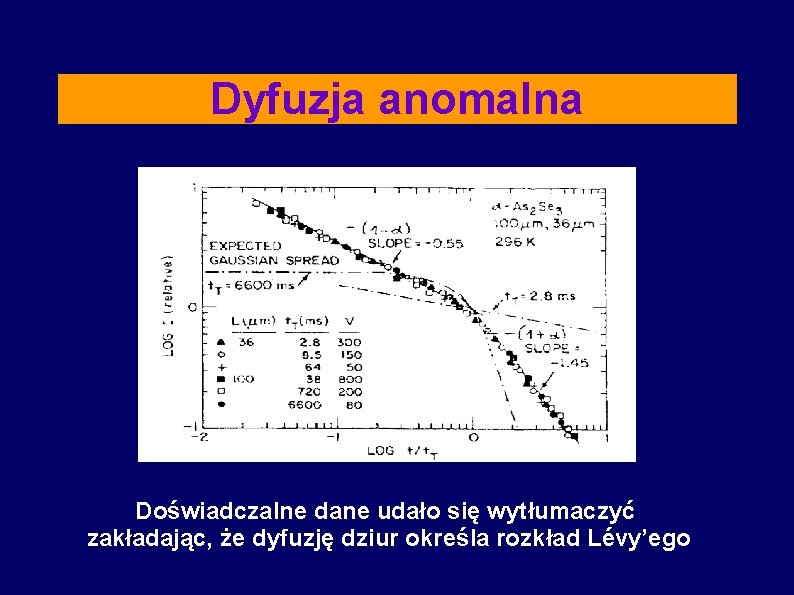
Dyfuzja anomalna Doświadczalne dane udało się wytłumaczyć zakładając, że dyfuzję dziur określa rozkład Lévy’ego

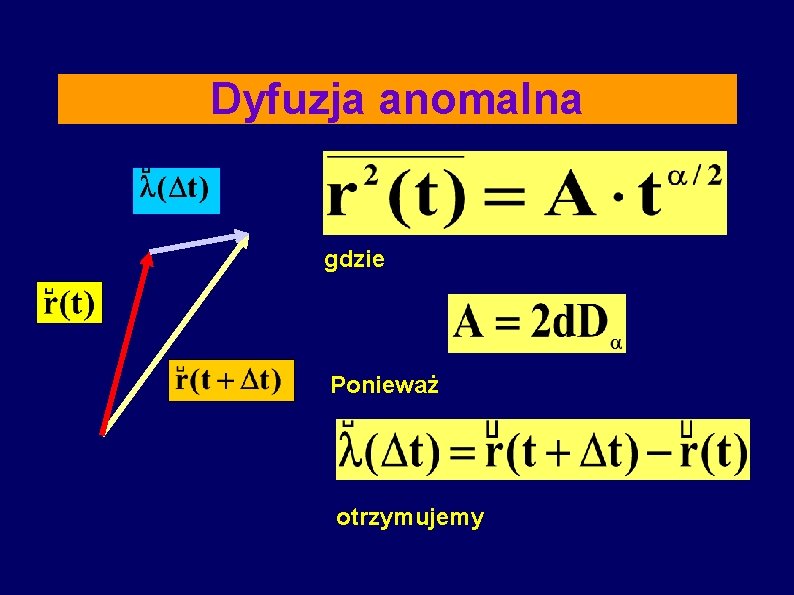
Dyfuzja anomalna gdzie Ponieważ otrzymujemy

Dyfuzja anomalna dla dyfuzji normalnej = 2 dla dyfuzji anomalnej < 1 A wiec w chwili t istnieje korelacja między wektorem określającym położenie cząstki r (t) i wektorem przemieszczenia cząstki ( t )

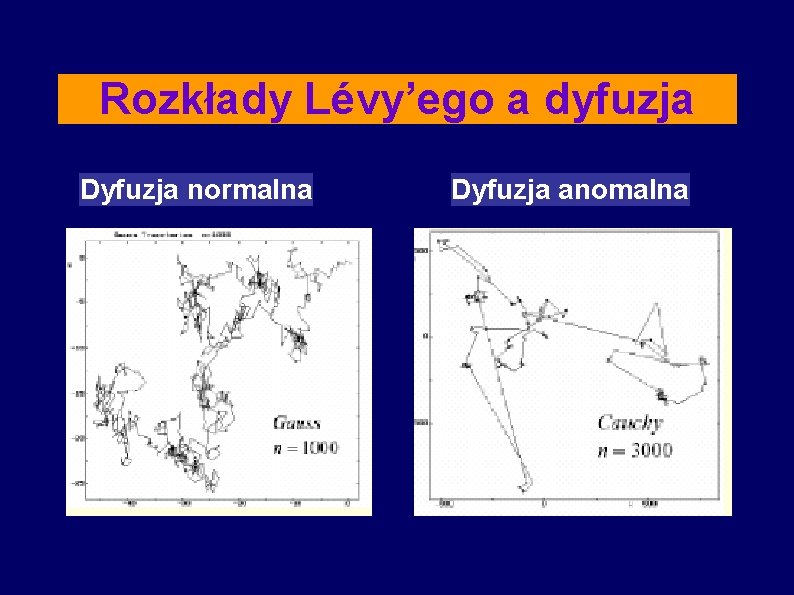
Rozkłady Lévy’ego a dyfuzja Dyfuzja normalna Dyfuzja anomalna

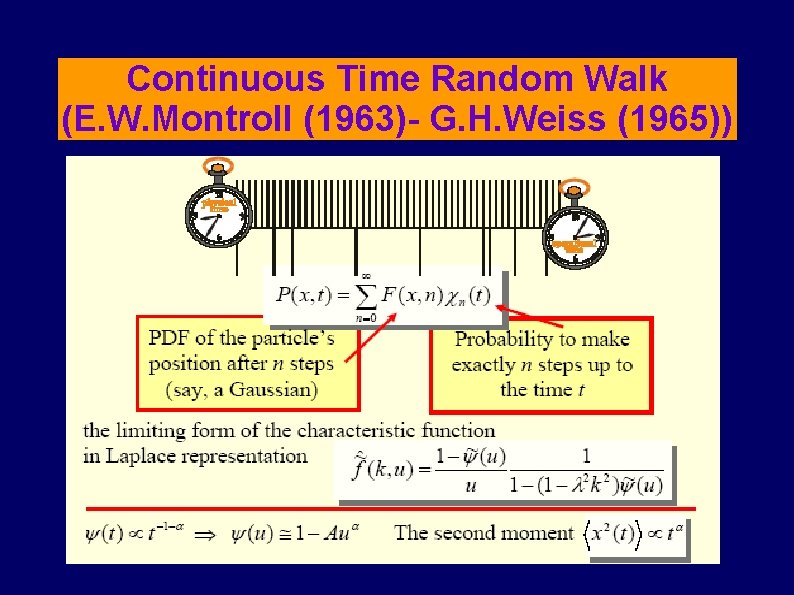
Continuous Time Random Walk (E. W. Montroll (1963)- G. H. Weiss (1965))

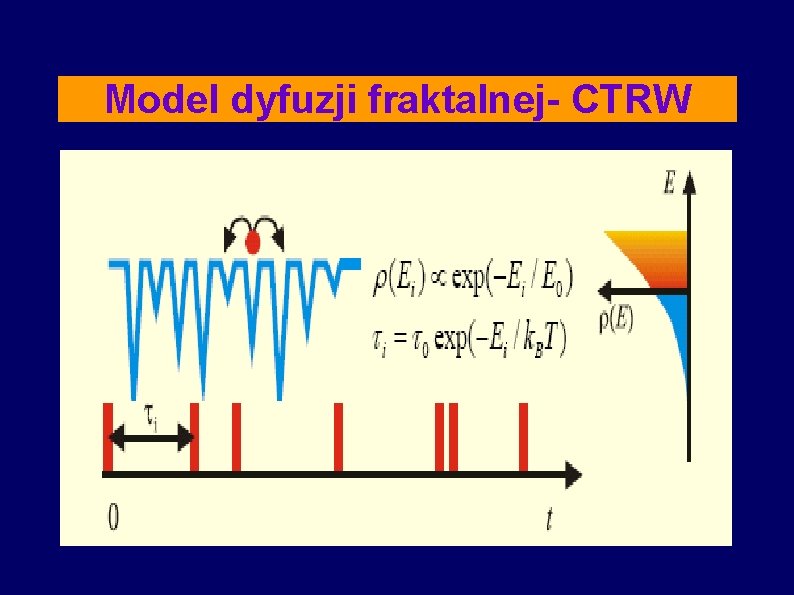
Model dyfuzji fraktalnej- CTRW

Dyfuzja normalna i anomalna Dyfuzja normalna Dyfuzja anomalna Równanie ruchu Średnie przemieszczenie Przemieszczenie cząstki przy dyfuzji anomalnej jest mniejsze niż przemieszczenie cząstki przy dyfuzji normalnej

Pochodna fraktalna - przykład

Pochodna fraktalna - definicja

Różniczkowanie fraktalne

Dyfuzja fraktalna Rozwiązanie równania dyfuzji anomalnej można wyrazić za pomocą tak zwanej funkcji specjalnej Foxa

Dyfuzja anomalna ● ● Transport elektronów, dziur, jonów, spinów itd. w nieuporządkowanych ciałach stałych (półprzewodniki, dielektryki, szkła spinowe, układy perkolujące, polimery, szkliste substancję itd. ) Dyfuzja cieczy, zawiesin w strukturach fraktalnych – substancje granulowane, górne oraz lodowcowe osady z kanałami o złożonej konfiuracji; kapilary w roślinach, krew, brzegowa strefa morza, nanostruktury, zeolity itd.

Dyfuzja fraktalna a ZFCS IF US ?

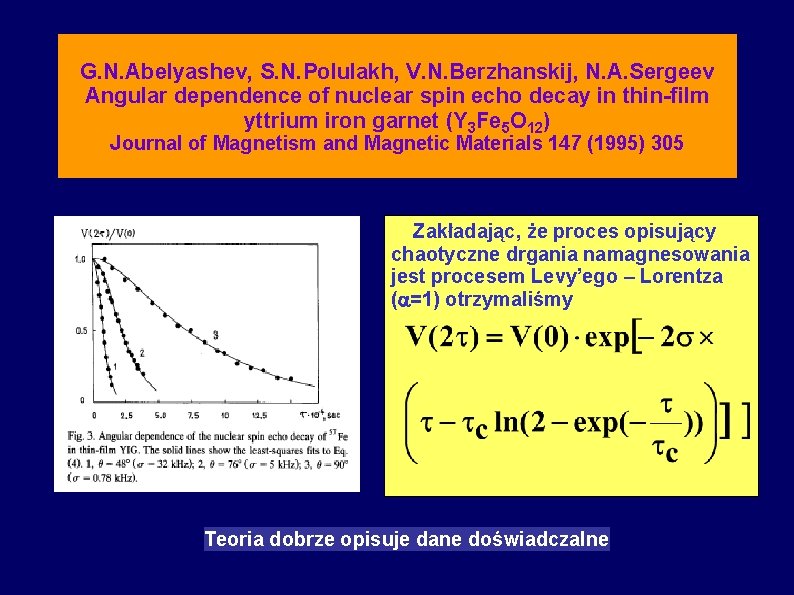
G. N. Abelyashev, S. N. Polulakh, V. N. Berzhanskij, N. A. Sergeev Angular dependence of nuclear spin echo decay in thin-film yttrium iron garnet (Y 3 Fe 5 O 12) Journal of Magnetism and Magnetic Materials 147 (1995) 305 Zakładając, że proces opisujący chaotyczne drgania namagnesowania jest procesem Levy’ego – Lorentza ( =1) otrzymaliśmy Teoria dobrze opisuje dane doświadczalne
![Natrolite Na 16Al 16 Si 24 О 80 16 H 2 O Mineralny Natrolite (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) Mineralny](https://slidetodoc.com/presentation_image_h2/a0d04246a1ef1c05c6ae994ae382f181/image-33.jpg)
Natrolite (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) Mineralny natrolit zawiera nanokanały w których znajdują się przestrzennie uporządkowane molekuły wody

Dyfuzja anomalna – proces niemarkowski (z „pamięcią”)
![Natrolit Na 16Al 16 Si 24 О 80 16 H 2 O M Natrolit (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) M.](https://slidetodoc.com/presentation_image_h2/a0d04246a1ef1c05c6ae994ae382f181/image-35.jpg)
Natrolit (Na 16[Al 16 Si 24 О 80] • 16 H 2 O) M. Olszewski, N. A. Sergeev, A. V. Sapiga. Non-Markovian dynamic and NMR spectra in solids. Z. Naturf. , v. 59 a, (2004) pp. 501 -504.

Zanik echa spinowego Dyfuzja normalna Dyfuzja anomalna

Relaksacja spin-sieć Dyfuzja normalna Dyfuzja fraktalna

„Migające” echa

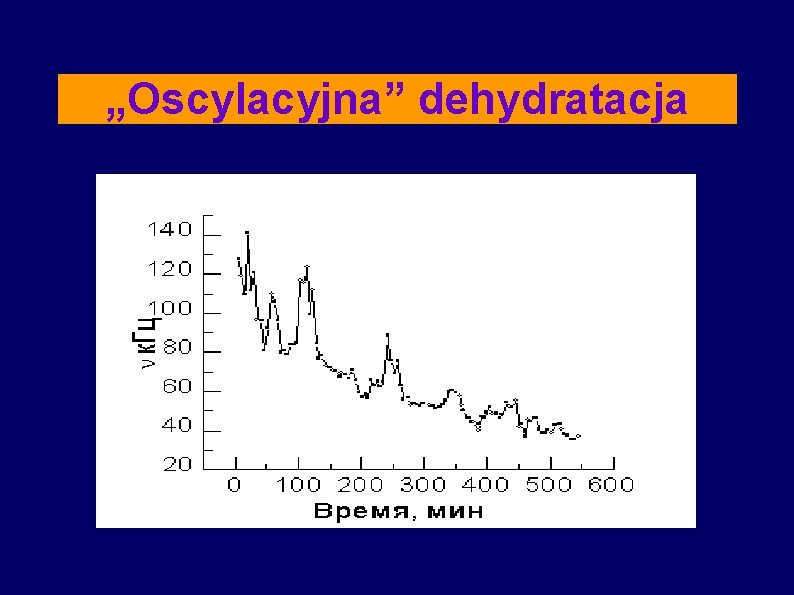
„Oscylacyjna” dehydratacja

Host-Guest Interactions in Natrolite under Pressure Yongjae Lee, Zhenxian Liu, Joseph A. Hriljac, Thomas Vogt We present here a nascent field of high pressure chemistry: the pressure and simultaneous temperature dependent interactions of guest molecules in zeolitic nanochannels. In natrolite channels (Na 16 Al 16 Si 24 O 80· 16 H 2 O), two distinctively overhydrated states (“pressureinduced hydration”) are observed under hydrostatic pressure (24 H 2 O near 1 GPa and 32 H 2 O above 1. 2 GPa), accompanied by anomalous volume swelling of the host zeolitic scaffolding (“pressure-induced expansion”). 1 -3 The resulting water nanostructures evolve with pressure and temperature. 4 Synchrotron X-ray powder diffraction study also suggest possible “pressureinduced absorption” of Ar from the pressure medium into the zeolitic channels. These observations are supported by high pressure IR spectroscopic measurements, which point to the resulting changes in the water vibrational frequencies upon the modification of the hostguest interactions. The high-pressure chemistry of zeolite host-guest systems thus opens a novel way to a possible tuning of the sorption capacity and ion exchange selectivity. 1. Lee, Y. , Vogt, T. , Hriljac, J. A. , Parise, J. B. , and Artioli, G. (2002) Pressure-Induced Volume Expansion of Zeolites in the Natrolite family. J. Am. Chem. Soc. , 124, 54665475. 2. Lee, Y. , Hriljac, J. A. , Parise, J. B. , and Vogt, T. (2005) Pressure-induced stabilization of ordered paranatrolite: a possible solution to the paranatrolite controversy. Letter to Am. Mineral. , 90, 252 -257. 3. Lee, Y. , Vogt, T. , Hriljac, J. A. , Parise, J. B. , Hanson, J. C. , and Kim, S. J. (2002) Nonframework cation migration and irreversible pressure-induced hydration in a zeolite. Nature, 420, 485 -4893. 4. Lee, Y. , Martin, C. D. , Parise, J. B. , Hriljac, J. A. , and Vogt, T. (2004) Formation and manipulation of confined water wires. Nano Lett. 4, 619 -621

The International Association for the Promotion of Co-operation with Scientists from the New Independent States (NIS) of the Former Soviet Union is an independent International Association formed by the European Community, European Union Member States and like-minded countries to promote East-West scientific co-operation between INTAS members and INTAS-NIS partner countries. INTAS supports both fundamental and applied research in all fields of science, such as: Physics; Chemistry; Life Sciences; Earth Sciences & Environment; Economics, Social & Human Sciences; Mathematics & IT; Space, Aeronautics & Engineering.

TITLE: Nuclear Magnetic Resonance and Molecular Dynamic study in porous media: water and ions dynamics in nanostructures (microporous media, zeolite, natrolite). Project Consortium: I. Team - Prof. Giuseppe B. Suffritti - Universita degli studi di Sassari, Dipartimento di Chimica, Italy II. Team – Prof. N. A. Sergeev - University of Szczecin, Institute of Physics, Poland III. Team – Dr. A. V. Sapiga - Tavrida National University, Simferopol, Ukraine ZAPRASZAMY DO WSPÓŁPRACY !!!

Przeglądy dotyczące dyfuzji fraktalnej 1. R. Kutner, „Niegaussowskie Procesy Stochastyczne w Świecie Realnym”- Wykład na UW - 2005 http: //primus. okwf. fuw. edu. pl/erka/Wyklad_monograficzny. html 2. J. Haus and K. W. Kehr, “Diffusion in Regular and Disordered Lattices”, Physics Reports 150 (1987) 263. 3. J. -P. Bouchaud and A. Georges, “Anomalous Diffusion in Disordered Media: Statistical Mechanisms, Models and Physical Applications”, Physics Reports 195 (1990) 127. 4. R. Metzler, J. Klafter, „The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach”, Physics Reports 339 (2000) 1.
 100 100 100 100 100
100 100 100 100 100 What's 100 + 100
What's 100 + 100 Box plot gcse
Box plot gcse Big data on bare metal
Big data on bare metal 200+200+300
200+200+300 Malloc lab 100/100
Malloc lab 100/100 100 + 100 200
100 + 100 200 38 sayısının 24 fazlasının 18 eksiği kaçtır
38 sayısının 24 fazlasının 18 eksiği kaçtır Números romanos del 200 al 500
Números romanos del 200 al 500 Héroïne dans la guerre de 100 ans (100 years war).
Héroïne dans la guerre de 100 ans (100 years war). C/100=f-32/180=k-273/100
C/100=f-32/180=k-273/100 200+200+100+100
200+200+100+100 200 + 200 + 300
200 + 200 + 300 100+100=200
100+100=200 Medo-lat epistemology
Medo-lat epistemology Bìa tiểu luận trường đại học đà lạt
Bìa tiểu luận trường đại học đà lạt Local guide program
Local guide program Scalene fissure
Scalene fissure Pierwsza koparka wykonala polowe wykopu w ciagu 6 h
Pierwsza koparka wykonala polowe wykopu w ciagu 6 h định mức hao hụt gạch ốp lát
định mức hao hụt gạch ốp lát Lat
Lat Auscultatory triangle of the back
Auscultatory triangle of the back Lat assurance
Lat assurance N cut fem lat
N cut fem lat Den uniforma gruppen
Den uniforma gruppen Ania i bogdan ważą razem 70 kg
Ania i bogdan ważą razem 70 kg Greater sciatic foramen
Greater sciatic foramen Ge lat
Ge lat Lat yegan joyni davolash
Lat yegan joyni davolash Lat prayer
Lat prayer Lat status
Lat status Pelvik grafi
Pelvik grafi Zanjirga ulangan katta po'lat ilgak
Zanjirga ulangan katta po'lat ilgak Cho'yan va po'lat
Cho'yan va po'lat Zakaz pokazywania dziewczyn do lat 14 w towarzystwie
Zakaz pokazywania dziewczyn do lat 14 w towarzystwie Thêu giáp tỉa
Thêu giáp tỉa Tà áo năm xưa xanh màu thông đà lạt
Tà áo năm xưa xanh màu thông đà lạt Urnordiska ord
Urnordiska ord Zuzia i kuba zbieraja znaczki
Zuzia i kuba zbieraja znaczki Inwentaryzacja biblioteki szkolnej
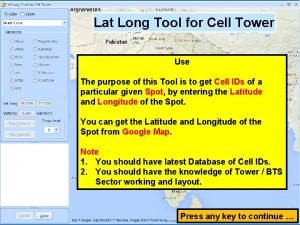
Inwentaryzacja biblioteki szkolnej Eiffel tower lat long
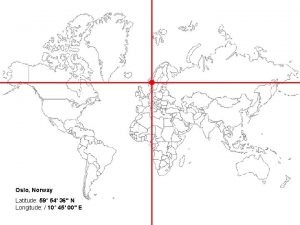
Eiffel tower lat long Oslo norway latitude and longitude
Oslo norway latitude and longitude Man lat
Man lat Qdx=200-2px qsx=-100+4px
Qdx=200-2px qsx=-100+4px