New Castep Functionality Linear response and nonlocal exchangecorrelation

New Castep Functionality Linear response and non-local exchange-correlation functionals Stewart Clark University of Durham, UK

The Authors of Castep l l l l Stewart Clark, Durham Matt Probert, York Chris Pickard, Cambridge Matt Segal, Cambridge Phil Hasnip, Cambridge Keith Refson, RAL Mike Payne, Cambridge

New Functionality l Linear response 1. 2. 3. 4. l Density functional perturbation theory Atomic perturbations (phonons) E-field perturbations (polarisabilities) k-point perturbations (Born charges) Non-local exchange-correlation 1. 2. 3. Summary of XC functionals Why use non-local functionals? Some examples

Density Functional Perturbation Theory l l Based on compute how the total energy responds to a perturbation, usually of the DFT external potential v Expand quantities (E, n, y, v) • Properties given by the derivatives

The Perturbations l Perturb the external potential (from the ionic cores and any external field): • • l Ionic positions Cell vectors Electric fields Magnetic fields phonons elastic constants dielectric response NMR But not only the potential, any perturbation to the Hamiltonian: • • d/dk d/d(PSP) Born effective charges alchemical perturbation

Phonon Perturbations l l l For each atom i at a time, in direction a=x, y or z This becomes perturbation denoted by l The potential becomes a function of perturbation l Take derivatives of the potential with respect to l Hartree, xc: derivatives of potentials done by chain rule with respect to n and l So we need this E(2)

The expression for phonon-E(2) • Superscripts denote the order of the perturbation • E(2) given by 0 th and 1 st order wave functions and densities • This is a variational quantity – use conjugate gradients minimiser • Constraint: 1 st order wave functions orthogonal to 0 th order wave functions • This expression gives the electronic contribution

The Variational Calculation l E(2) is variational with respect to |y(1)> The plane-wave coefficients are varied to find the minimum E(2) under a perturbation • • • l l l of a given ion i in a given direction a and for a given q Analogous to standard total energy calculation Based on a ground state (E(0)) calculation Can be used for any q value

Sequence of calculation Find electronic force constant matrix l Add in Ewald part l Repeat for a mesh of q And with Fourier interpolation: l Fourier transform to get F(R) l Fit and interpolate l Fourier transform and mass weight to get D at any q l

Phonon LR: For and against l For • Fast, each wavevector component about the • • • l same as a single point energy calculation No supercells requires Arbitrary q General formalism Against • Details of implementation considerable

Symmetry Considerations l l When perturbing the system the symmetry is broken No time reversal symmetry Implication is: k-point number increases For example, Phonon-Si 2 (Diamond): 6 x 6 x 6 MP set, 48 symmetry operations leads to SCF 28 k-points q=(0, 0, 0), 48 symmetry elements q=(1/2, 0, 0), 12 symmetry elements x-displacement leaves 12 elements y-displacement leaves 4 elements 72 k-points for E(2) 108 k-points for E(2) q=arbitrary, leaves only identity element and needs 216 k-points

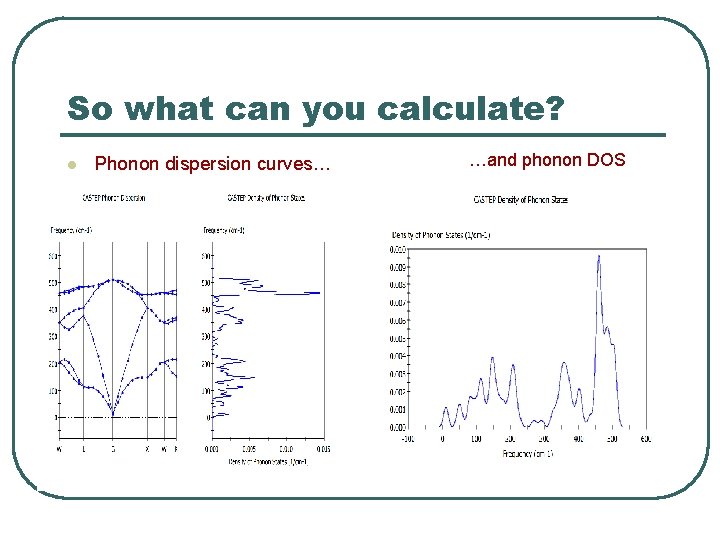
So what can you calculate? l Phonon dispersion curves… …and phonon DOS

Thermodynamics l Phonon density of states Debye temperature l Phase stability via l Entropic terms – derivatives of free energy Vibrational specific heats l l

Electric Field Response l l l Bulk polarisability Born effective charges Phonon G-point LO/TO splitting Dielectric permittivities IR spectra Raman Spectra

Why Electric Fields l l Need Born effective charges to get LO-TO splitting: originates from finite dipole per unit cell Example given later… Found from d/dk calculation and similar cross-derivative expressions Technical note: this means that all expressions for perturbed potentials different at zone centre than elsewhere

Examples of E-field Linear Response • Response of silicon to an electric field perturbation • Plot shows first order charge density Blue: where electrons are removed Yellow: where electrons go Acknowledgement: E-field work by my Ph. D student Paul Tulip

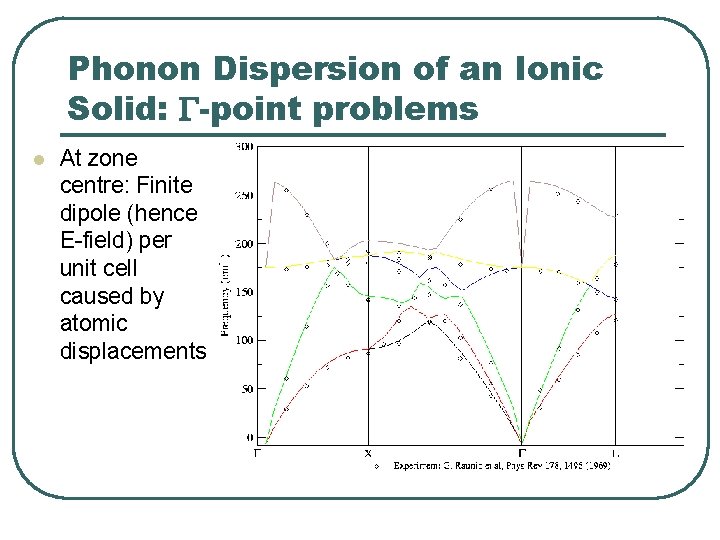
Phonon Dispersion of an Ionic Solid: G-point problems l At zone centre: Finite dipole (hence E-field) per unit cell caused by atomic displacements

E-field on a polar system: Na. Cl l l Without E-field: LO/TO Frequencies: 175 cm-1 Born charge: Na Cl Ionic character as expected: Na+ and Cl- ions LO/TO splitting is 90 cm-1: Smooth dispersion curve at the G-point • Polarisability Tensor • Electronic Permittivity Tensor Quantities given in atomic units

Summary of Density Functional Perturbation Theory l l l Phonon frequencies Phonon DOS Debye Temperate PVT phase diagrams Vibrational specific heats Born effective charges LO/TO Splitting Bulk polarisabilities Electric permittivities First order charge densities (where electrons move from and to) Etc… Lots of new physics…and more planned in later releases

Non-local XC functionals l l l Basic background of XC interaction Description within LDA and GGAs Some non-local XC functional Implementation within Castep Model test cases

The exchange-correlation interaction Many body Hamiltonian – many body wavefunction Kohn-Sham Hamiltonian – single particle wavefunction Single particle KE – not many body Hartree requires self-interaction correction All goes in here

Approximations to XC l l l Local density approximation – only one Generalised gradient approximations – lots GGA’s + Laplacians – no real improvements Meta-GGA’s (GGA + Laplacian + KE) – many recent papers – but nothing exciting yet. Hybrid functionals (GGA/meta-GGA + some exact exchange from HF calculations) – currently favoured by the chemistry community. Exc[n(r, r’)] – has been generally ignored recently by DFT community (although QMC and GW show it to have several interesting properties!).

New Functionals: The CPU cost l l l We aim to go beyond the local (LDA) or semilocal (GGA) approximations Why? Cannot get any higher accuracy with these class of functionals The computational cost is high: scaling will be O(N 2) or O(N 3) This is because all pairs (or more) of electrons must be considered That is, beyond the single particle model most DFT users are familiar with

First Class of New XC Functional: Exact and Screened Exchange l Exact Exchange (Hartree-Fock): l Screened Exchange: l And in terms of plane waves:

Why Exact/Screened Exchange? l l Exact exchange gives us access to the common empirical “chemistry” GGA functionals such as B 3 LYP Screened exchange can lead to accurate band gaps in semiconductors and insulators, so improved excitation energies and optical properties The cost: scales O(N 3), N=number of pl. waves LDA/GGA is 0. 1% of calculation, EXX is 99. 9%

Silicon Band Structure Extra cost can be worthwhile Some recent results (by my Ph. D student, Michael Gibson) • • LDA band gap: 0. 54 e. V Exact Exchange band gap: 2. 15 e. V Screened Exchange band gap: 1. 11 e. V Experimental band gap: 1. 12 e. V

Another approach: Some theory on exchange-correlation holes… l The exact(!) XC energy within DFT can be written as • Relationship defined as the Coulomb energy between an electron and the XC hole nxc(r, r’) • XC hole is described in terms of the electron pair-correlation function Determines probability of finding an electron at position r’ given one exists at position r

Properties of the XC hole l Pauli exclusion principle: gxc obeys the sum rule • The size of the XC hole is exactly one electron – mathematically, this is the Pauli exclusion principle • The LDA and some GGAs obey this rule • For a universal XC function (applicable without bias), it must obey as many (all!) exact conditions as possible

The Weighted Density Method l In the WDA the pair-correlation function is approximated by • The weighted density is fixed at each point by enforcing the sum rule • This retains the non-locality of the function along with the Coulomb-like integral for Exc[n]

The XC potential l l XC potential is determined in the usual manner (density derivative of XC energy) We get 3 terms where

Example of WDA in action: An inhomogeneous electron gas l Investigate inhomogeneous systems by applying an external potential of the form • Very accurate quantum Monte Carlo results which to compare • Will have no pseudopotential effects • It’s inhomogeneous! • Given a converged plane wave basis set, we are testing the XC functional only – nothing else to consider

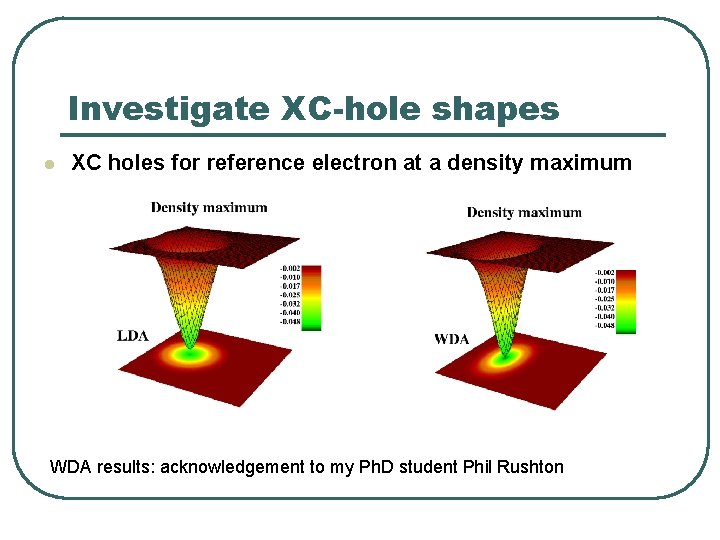
Investigate XC-hole shapes l XC holes for reference electron at a density maximum WDA results: acknowledgement to my Ph. D student Phil Rushton

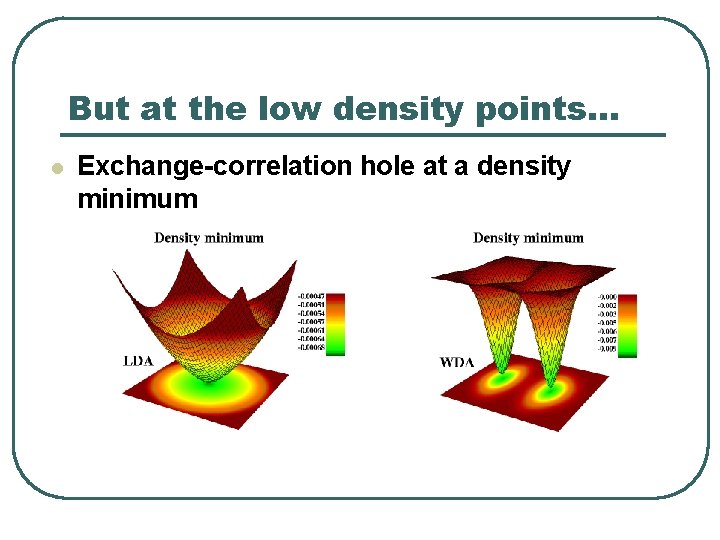
But at the low density points… l Exchange-correlation hole at a density minimum

How accurate are the XC holes? l Compare to VMC data – M. Nekovee, W. M. C. Foulkes and R. J. Needs PRL 87, 036401 (2001)

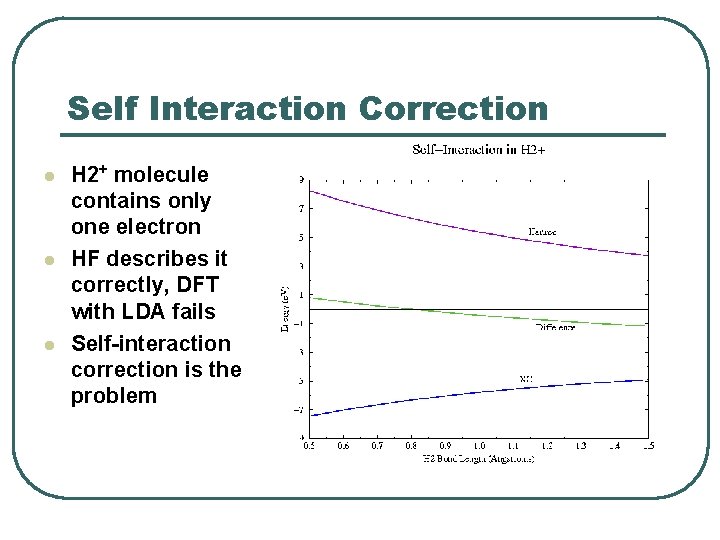
Self Interaction Correction l l l H 2+ molecule contains only one electron HF describes it correctly, DFT with LDA fails Self-interaction correction is the problem

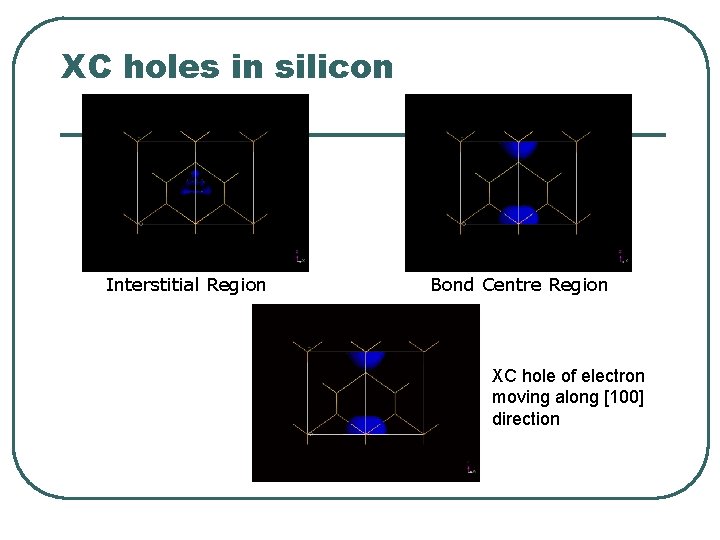
Realistic Systems - Silicon l l Generate self-consistent silicon charge density Examine XC holes at various points Si [110] plane

XC holes in silicon Interstitial Region Bond Centre Region XC hole of electron moving along [100] direction

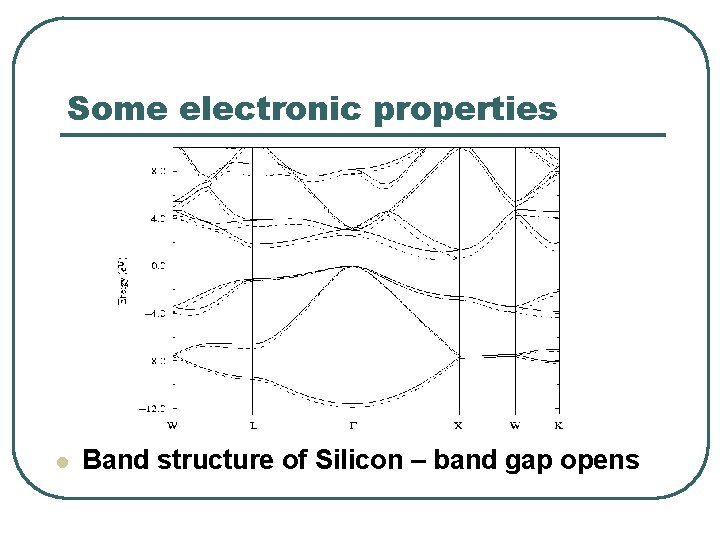
Some electronic properties l Band structure of Silicon – band gap opens

III-V semiconductor band gaps Band gaps in e. V l The non-local potential opens up the band gap of some simple semiconductors

Timescales The following is my list of developments - other CGD members have other new physics and new improvements l l l l First implementation of phonon linear response already in Castep v 2. 2 Much faster (3 -4 times faster) phonon linear response due to algorithmic improvements in Castep v 3. 0 Phonon linear response calculations for metals under development. Aimed to be in v 3. 0 or v 3. 1 Electric field response (Born charges, bulk polarisabilities, permittivity, LO/TO splitting) in Castep v 3. 0 Exact and screened exchange: currently being tested and developed aimed at the v 3. 0 release Weighted density method: currently working and tested – release schedule under discussion Raman and IR intensities currently being implemented. Scientific evaluation still be performed before a possible release can be discussed