Nattee Niparnan GRAPH ALGORITHM Graph A pair G

Nattee Niparnan GRAPH ALGORITHM

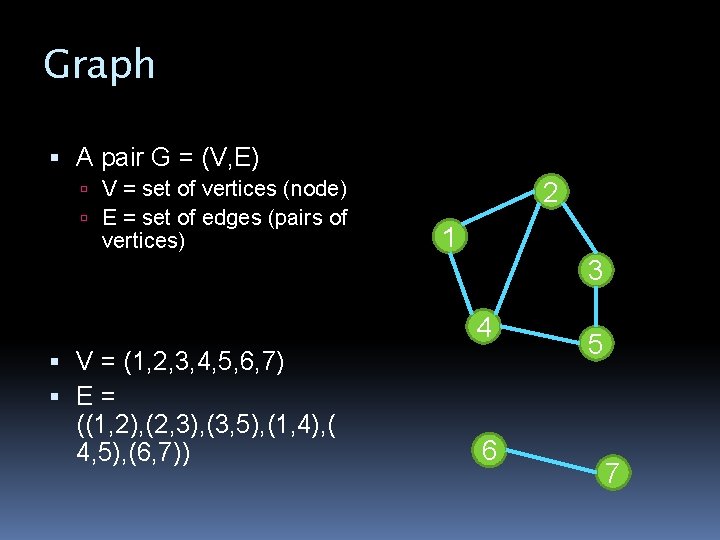
Graph A pair G = (V, E) V = set of vertices (node) E = set of edges (pairs of vertices) 2 1 3 4 V = (1, 2, 3, 4, 5, 6, 7) E= ((1, 2), (2, 3), (3, 5), (1, 4), ( 4, 5), (6, 7)) 6 5 7

Term you should already know directed, undirected graph Weighted graph Bipartite graph Tree Spanning tree Path, simple path Circuit, simple circuit Degree

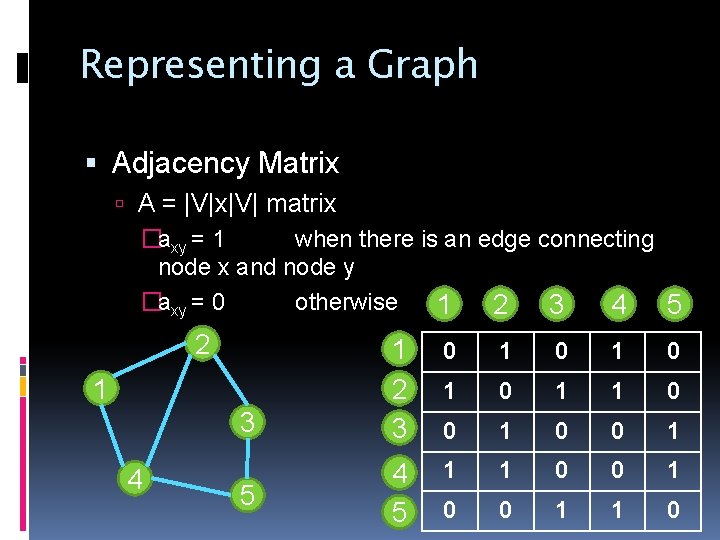
Representing a Graph Adjacency Matrix A = |V|x|V| matrix �axy = 1 when there is an edge connecting node x and node y �axy = 0 otherwise 1 2 3 4 5 2 1 3 4 5 1 2 3 0 1 0 1 1 0 0 1 4 5 1 1 0 0 1 1 0

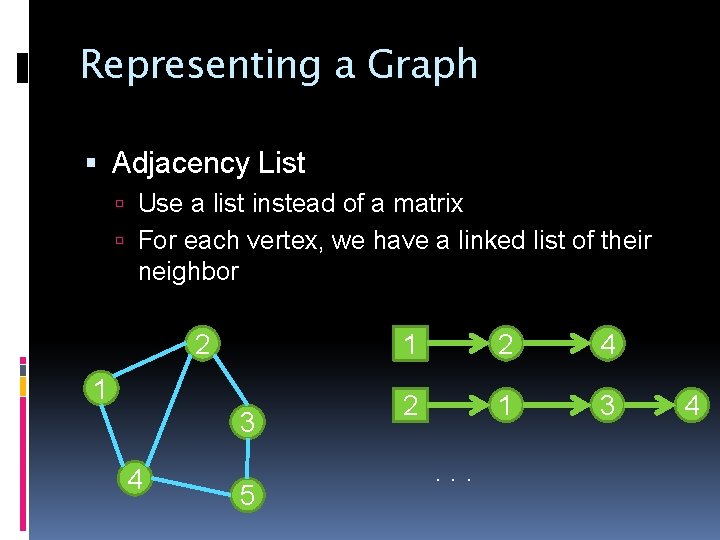
Representing a Graph Adjacency List Use a list instead of a matrix For each vertex, we have a linked list of their neighbor 2 1 3 4 5 1 2 4 2 1 3 . . . 4

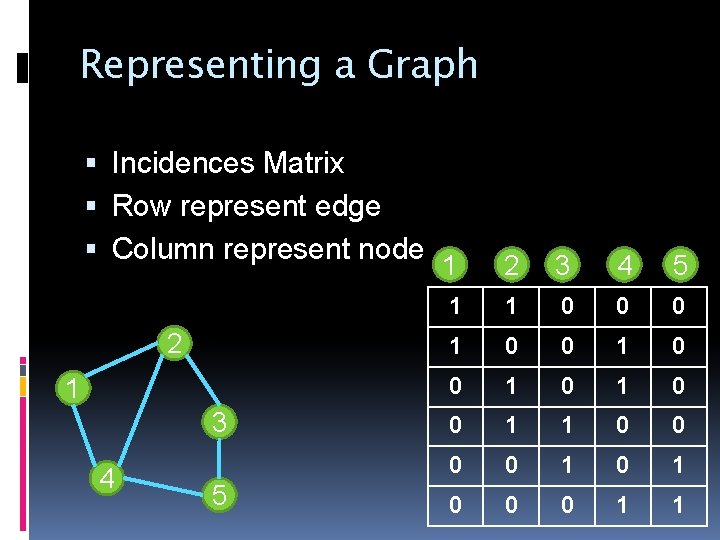
Representing a Graph Incidences Matrix Row represent edge Column represent node 2 1 3 4 5 1 2 3 4 5 1 1 0 0 0 1 0 0 1 1 0 0 0 1 1

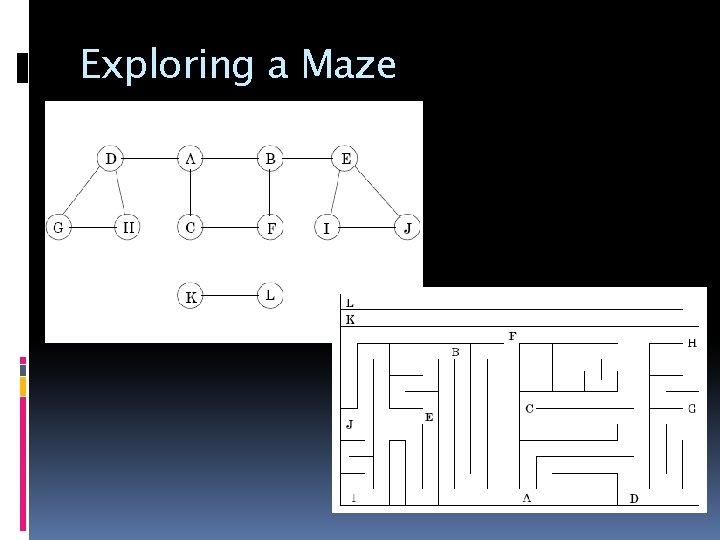
Exploring a Maze

Exploring Problem Input: A Graph �Maybe as an adjacency matrix A Starting node Output: List of node reachable from v �Maybe as an array indexed by a node

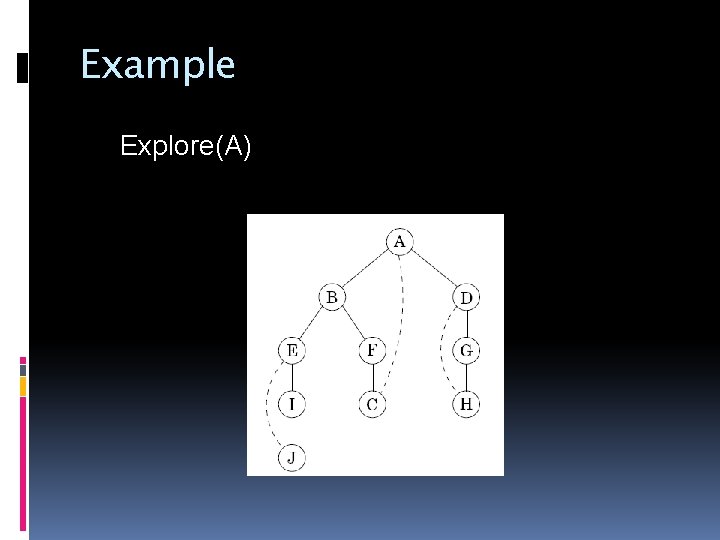
Depth-First-Search procedure explore(G; v) // Input: G = (V; E) is a graph; v V // Output: visited(u) is set to true for all nodes u reachable from v { visited(v) = true previsit(v) for each edge (v, u) E if not visited(u) explore(u) postvisit(v) }

Example Explore(A)

Extend to Graph Traversal is walking in the graph We might need to visit each component in the graph Can be done using explore Do “explore” on all non-visited node The result is that we will visit every node What is the difference between just looking into V (the set of vertices? )

Graph Traversal using DFS procedure dfs(G) { for all v V visited(v) = false for all v V if not visited(v) explore(v) }

Complexity Analysis Each node is visited once Each edge is visited twice Why? O( |V| + |E|)

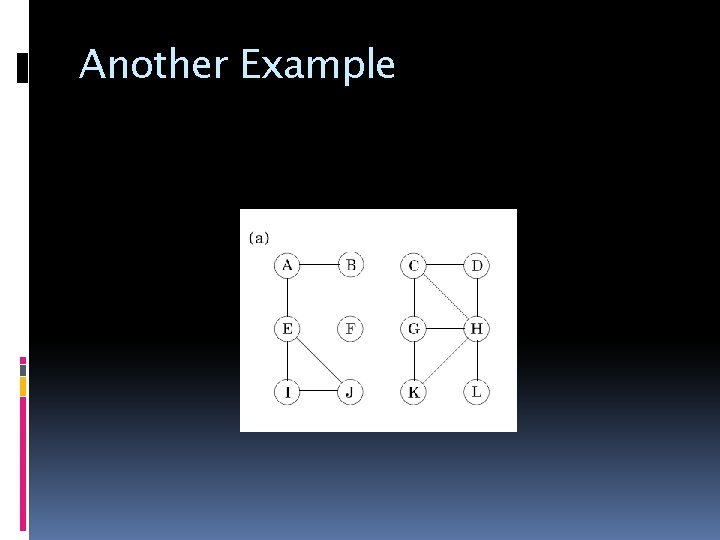
Another Example

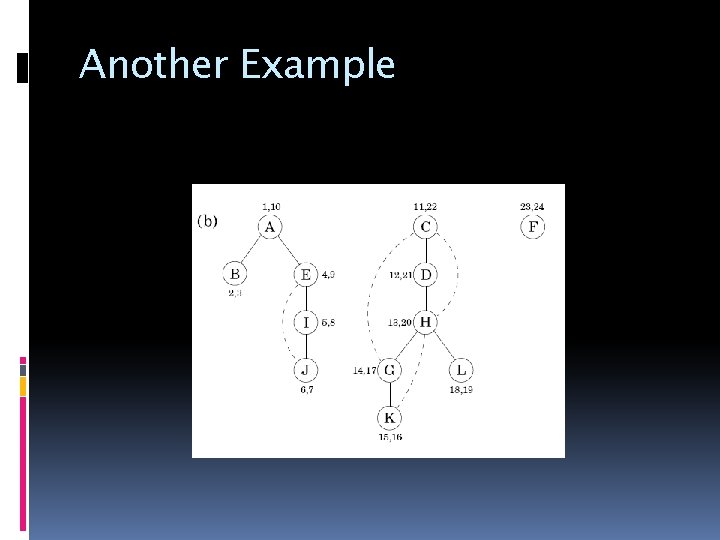
Another Example

Connectivity in Undirected Graph If can reach Then �Also && can reach Divide into smaller subset of vertices that can reach other

Connected Component Problem Input: A graph Output: Marking in every vertices identify the connected component �Let it be an array ccnum, indexed by vertices

Solution Define global variable cc In previsit() ccnum[v] = cc Before calling each explore cc++

Ordering in Visit procedure previsit(v) pre[v] = clock + 1 procedure postvisit(v) post[v] = clock + 1

Ordering in Visit • The interval for node u is [pre(u), post(u)] • The inverval for u, v is either • Contained • disjointed • Never intersect

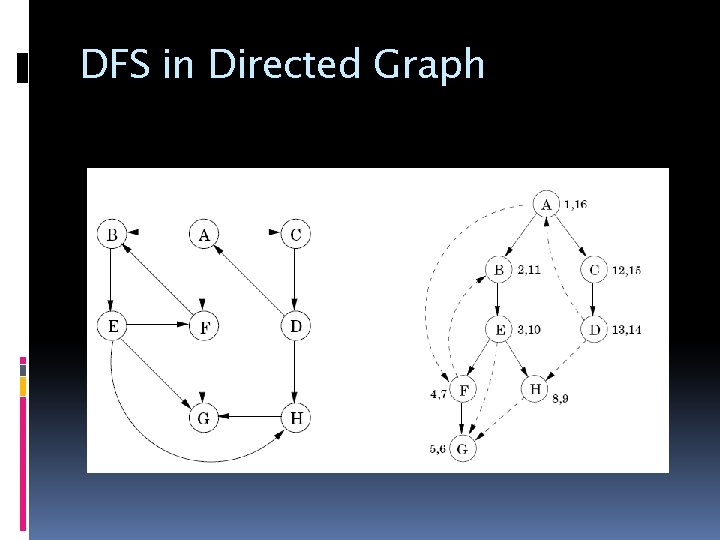
DFS in Directed Graph

Type of Edge in Directed Graph

Directed Acyclic Graph (DAG) A directed Graph without a cycle Has “source” �A node having only “out” edge Has “sink” �A node having only “in” edge How can we detect that a graph is a DAG What should be the property of “source” and “sink” ?

Solution A directed graph is acyclic if and only if it has no back edge Sink Having lowest post number Source Having highest post number

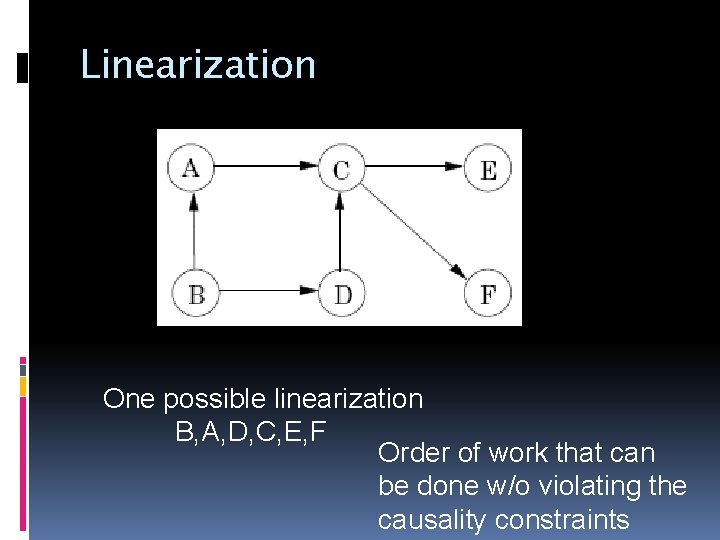
Linearization of Graph for DAG, we can have an ordering of node Think of an edge as Causality Time-dependency � means has to be done before Linearization ordering of node by causality

Linearization One possible linearization B, A, D, C, E, F Order of work that can be done w/o violating the causality constraints

Topological Sorting Problem Input: A DAG (non-dag cannot be linearized) Output: A sequence of vertices �If we have a path from to � must come before in the sequence

Topological Sorting Do DFS List node by post number (descending) 3, 8 4, 5 2, 9 6, 7 1, 12 10, 1