Proximity Closest pair divideandconquer Closest pair CLOSEST PAIR

Proximity Closest pair, divide-and-conquer Closest pair CLOSEST PAIR INSTANCE: Set S = {p 1, p 2, . . . , p. N} of N points in the plane. QUESTION: Determine the two points of S whose mutual distance is smallest. We’ve seen a proof that CLOSEST PAIR has a lower bound for time (N log N). We seek an algorithm with upper bound O(N log N). If found, these together imply that CLOSEST PAIR (N log N). Two algorithm paradigms come to mind for O(N log N): 1. Sorting 2. Divide-and-conquer To use sorting, a total ordering of the points is needed, but none seem useful. For example, projecting the points of S onto the y axis give a total ordering on y coordinate but destroys useful information: points p 1 and p 2 are closest in Euclidean distance but farthest in y distance.

Proximity Closest pair, divide-and-conquer Divide-and-conquer, concept Using the divide-and-conquer paradigm, time in O(N log N) can be achieved by: 1. Dividing the problem into two equal-sized subproblems 2. Solving those subproblems recursively 3. Merging the subproblem solutions into an overall solution in linear O(N) time. Unfortunately, it is not immediately obvious how to perform the merge in linear time. Suppose the problem has been solved for subproblem sets S 1 and S 2, where S 1 S 2 = S, S 1 S 2 = , |S 1| |S 2| N/2; giving a closest pair of points for S 1 and another for S 2. How can the closest pair for S be found? It may consist of one point from S 1 and one from S 2. Testing all possible pairs of points from S 1 and S 2 requires time in O(N/2) · O(N/2) O(N 2), which is unsatisfactory. S 1 S 2

Proximity Closest pair, divide-and-conquer Divide-and-conquer for d = 1, 1 We consider a divide-and-conquer algorithm for CLOSEST PAIR in 1 dimension (d = 1). Partition S, a set of points on a line, into two sets S 1 and S 2 at some point m such that for every point p S 1 and q S 2, p < q. Solving CLOSEST PAIR recursively on S 1 and S 2 separately produces {p 1, p 2}, the closest pair in S 1, and {q 1, q 2}, the closest pair in S 2. Let be the smallest distance found so far: = min(|p 2 - p 1|, |q 2 - q 1|) The closest pair in S is either {p 1, p 2} or {q 1, q 2} or some {p 3, q 3} with p 3 S 1 and q 3 S 2. S 1 p 2 S 2 p 3 q 3 m q 1 q 2

Proximity Closest pair, divide-and-conquer Divide-and-conquer for d = 1, 2 To check for such a point {p 3, q 3}, is it necessary to test every possible pair of points in S 1 and S 2? Note that if {p 3, q 3} is to be closer than (i. e. , |q 3 - p 3| < ), then both p 3 and q 3 must be within of m. How many points of S 1 can lie within of m, i. e. , within the interval (m - , m]? Because is the distance between the closest pair in either S 1 or S 2, a semi-closed interval of length can contain at most 1 point. For the same reason, there can be at most 1 point of S 2 within of m, i. e. , in the interval [m, m + ). So, the number of distance computations needed to check for a closest pair {p 3, q 3} with p 3 S 1 and q 3 S 2 is 1, not O(N 2). Finding any points in the intervals (m - , m] and [m, m + ) to do the computation can take at most O(N) time, giving a linear merge step. Thus a divide-and-conquer algorithm can solve 1 -dimensional CLOSEST PAIR in O(N log N) time. S 1 S 2 p 1 p 2 p 3 q 3 m q 1 q 2

Proximity Closest pair, divide-and-conquer Divide-and-conquer for d = 1, 3 procedure CPAIR 1(S) Input: X[1: N], N points of S in one dimension. Output: , the distance between the two closest points. 1 begin 2 if (|S| = 2) then 3 = |X[2] - X[1]| 4 else if (|S| = 1) then 5 = 6 else 7 begin 8 Construct(S 1, S 2) /* S 1 = {p: p m}, S 2 = {p: p > m} */ 9 1 = CPAIR 1(S 1) 10 2 = CPAIR 1(S 2) 11 p = max(S 1) 12 q = min(S 2) 13 = min( 1, 2, q - p) 14 end 15 endif 16 return 17 end Caveat Note that p (= p 3) and q (= q 3) are found not by looking within intervals (m - , m] and [m, m + ), but by identifying the two points closest to m. This works for d = 1 but not for d 2. For that reason the idea of p 3 and q 3 within of m was introduced.

Proximity Closest pair, divide-and-conquer Generalizing to d = 2 Partition two dimensional set S into subsets S 1 and S 2 such that every point of S 1 lies to the left of every point of S 2. To do so, cut S by vertical line l at the median x coordinate of S. Solve the problem recursively on S 1 and S 2. Let {p 1, p 2} be the closest pair in S 1 and {q 1, q 2} in S 2. 1 = distance(p 1, p 2) and 2 = distance(q 1, q 2) are the minimum separations in S 1 and S 2 respectively. = min( 1, 2) S 1 l S 2 p 1 1 p 2 q 1 q 2 2

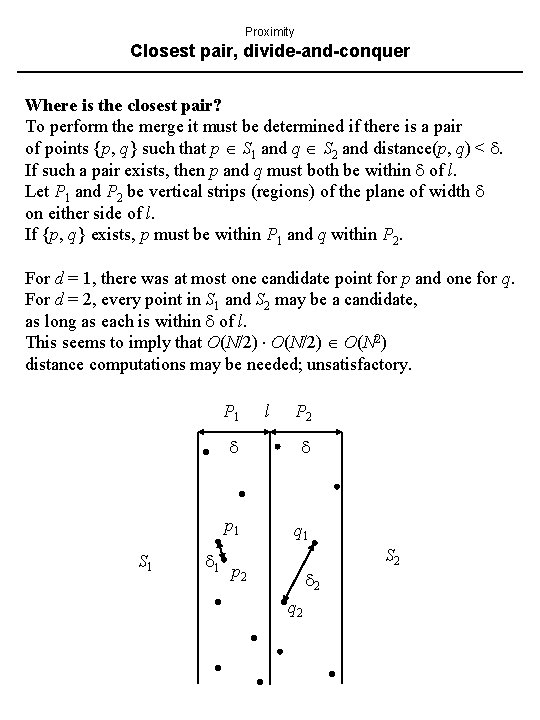
Proximity Closest pair, divide-and-conquer Where is the closest pair? To perform the merge it must be determined if there is a pair of points {p, q} such that p S 1 and q S 2 and distance(p, q) < . If such a pair exists, then p and q must both be within of l. Let P 1 and P 2 be vertical strips (regions) of the plane of width on either side of l. If {p, q} exists, p must be within P 1 and q within P 2. For d = 1, there was at most one candidate point for p and one for q. For d = 2, every point in S 1 and S 2 may be a candidate, as long as each is within of l. This seems to imply that O(N/2) O(N 2) distance computations may be needed; unsatisfactory. P 1 S 1 1 l P 2 p 1 q 1 p 2 2 q 2 S 2

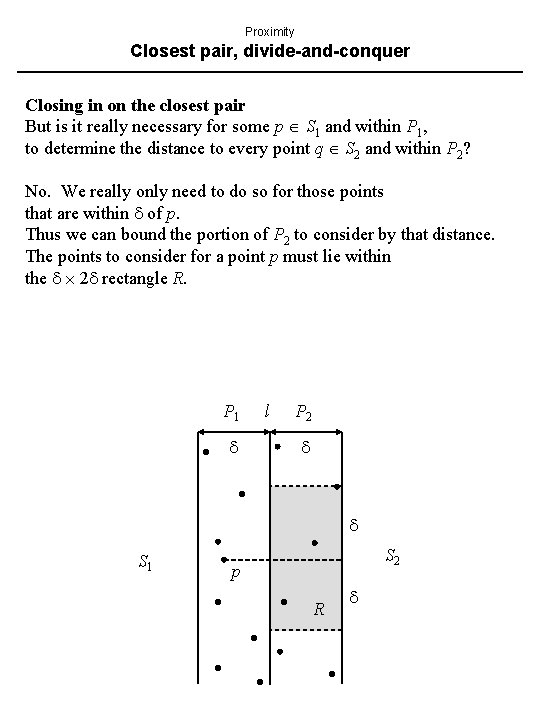
Proximity Closest pair, divide-and-conquer Closing in on the closest pair But is it really necessary for some p S 1 and within P 1, to determine the distance to every point q S 2 and within P 2? No. We really only need to do so for those points that are within of p. Thus we can bound the portion of P 2 to consider by that distance. The points to consider for a point p must lie within the 2 rectangle R. P 1 l P 2 S 1 S 2 p R

Proximity Closest pair, divide-and-conquer Distance computations required How many points can there be in rectangle R? Recall that no two points in P 2 are closer than . Because rectangle R has size 2 , there can be at most 6 points within it; any more and they would be closer than , a contradiction. This means that for each of the O(N/2) points p S 1 within P 1, only 6 points must be checked, not O(N/2) for each, so 6 O(N/2) = O(3 N) O(N) distance comparisons are needed in the merge step, not O(N 2). An O(N log N) algorithm for CLOSEST PAIR is possible. P 1 l P 2 S 1 S 2 p R

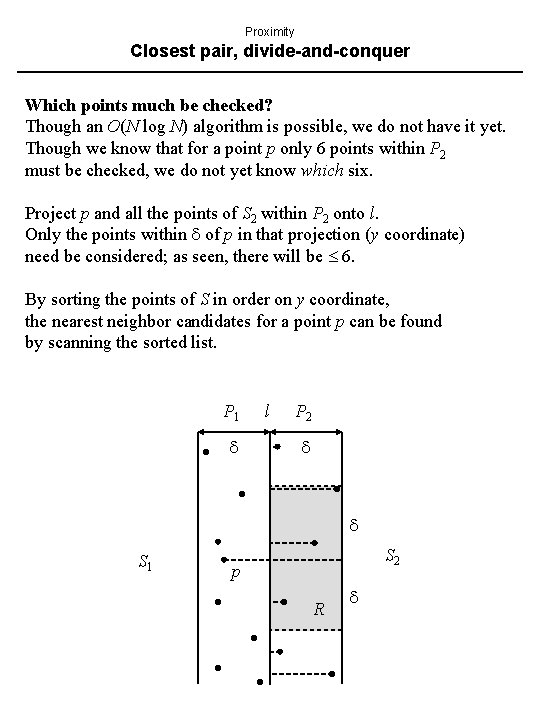
Proximity Closest pair, divide-and-conquer Which points much be checked? Though an O(N log N) algorithm is possible, we do not have it yet. Though we know that for a point p only 6 points within P 2 must be checked, we do not yet know which six. Project p and all the points of S 2 within P 2 onto l. Only the points within of p in that projection (y coordinate) need be considered; as seen, there will be 6. By sorting the points of S in order on y coordinate, the nearest neighbor candidates for a point p can be found by scanning the sorted list. P 1 l P 2 S 1 S 2 p R

Proximity Closest pair, divide-and-conquer Closest pair algorithm Algorithm from Preparata, p. 198: 1. Partition S into two subsets, S 1 and S 2, about the vertical median line l. 2. Find the closest pair separations 1 and 2 recursively. 3. = min( 1, 2) 4. Let P 1 be the set of points of S 1 that are within of the dividing line l and let P 2 be the corresponding subset of S 2. Project P 1 and P 2 onto l and sort by y coordinate. Let P 1* and P 2* be the two sorted sequences, respectively. 5. The “merge” may be carried out by scanning P 1* and for each point in P 1* inspecting the points of P 2* within distance . While a pointer advances on P 1*, the pointer of P 2* may oscillate within an interval of width 2. Let 1 be the smallest distance of any pair thus examined. 6. S = min( , 1) Step 4 appears to put an O(N log N) sort into each merge. It seems to have been written that way for clarity only. To achieve an O(N) merge, all the points of S are sorted at the start of the algorithm (“presorting”). The sorted sequences P 1* and P 2* are obtained in O(N) time from the presorted list.

Proximity Closest pair, divide-and-conquer Merge process algorithm Preparata p. 199 says: “… when executing Step 4, extract the points from the list in sorted order in only O(N) time. ” One way to assemble P 1*, for example, follows. Let Y be the presorted points of S, i. e. , an array of size N storing the points of S in order by ascending y coordinate; each entry has three fields: x, y, and active. Let P 1* be an array of size N with two fields: index and y. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 for i = 1 to N /* Initialize P 1*. */ P 1*[i]. index = 0 P 1*[i]. y = 0 endfor every point pi S Y[i]. active = FALSE endfor every point pi S 1 /* Mark the points of P 1* in Y. */ Y[i]. active = TRUE endfor j=1 for i = 1 to N /* Retrieve the points in sorted order. */ if Y[i]. active = TRUE P 1*[j]. index = i /* Points to Y for coordinate retrieval. */ j=j+1 endif endfor

Proximity Closest pair, divide-and-conquer Analysis Let T(N) be the running time of the algorithm on N points. The steps of CPAIR 2 require: 1. O(N) 2. 2 T(N/2) 3. O(1) 4. O(N) 5. O(N) 6. O(1) Thus, T(N) = 2 T(N/2) + O(N) O(N log N). The presort of S on y coordinate also requires O(N log N) time. Overall time for the CPAIR 2 algorithm to solve the CLOSEST PAIR problem for d = 2 is O(N log N). Because CLOSEST PAIR problem for d = 2 has a lower bound in (N log N) for any algorithm, this complexity is optimal, i. e. , (N log N).

Proximity Closest pair, divide-and-conquer Closest pair for d > 2 Preparata p. 199 -204 discusses solving CLOSEST PAIR using a divide-and-conquer algorithm for d > 3. The approach depends on the notion of sparsity, a measure of how many points can be in a d-dimensional hypercube with sides that measure 2. We made use of sparsity in the d = 1 and d = 2 case. The result is that the closest pair of points in a set of N points in Ed can be found in (N log N) time.