GENERATE AND TEST FRAMEWORK Nattee Niparnan OPTIMIZATION EXAMPLE



























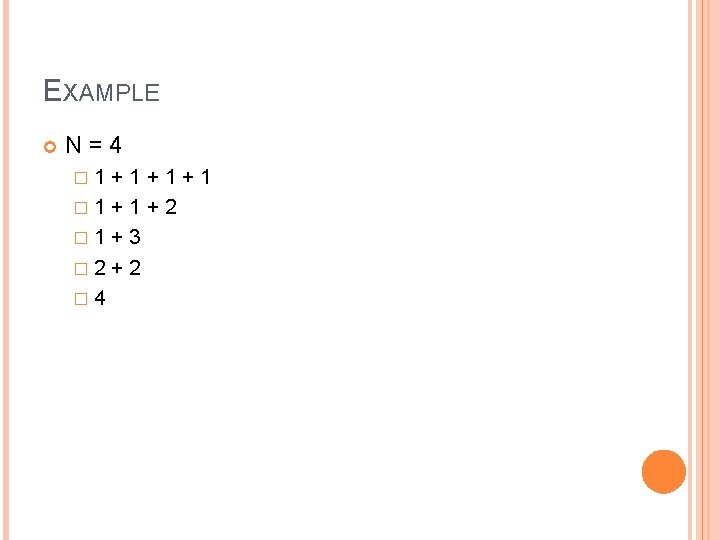















- Slides: 56

GENERATE AND TEST FRAMEWORK Nattee Niparnan

OPTIMIZATION EXAMPLE: FINDING MAX VALUE IN AN ARRAY 25 2 34 43 4 There 9 -5 87 0 are N possible answers � The first element � The second element � 3 rd, 4 th … Try 0 all of them � Remember the best one 5 6 1

GENERATE AND TEST FRAMEWORK Define the set of admissible solution Generate all of them ( For each generated solution whether it is the one we want � By the “evaluation” function ( ) � Test � for ) optimization: remember the best one so far � For decision: report when we found the “correct” one

COMBINATION AND PERMUTATION In many case, the set of the admissible solutions is a set of “combination” or “permutation” of something We need to knows how to generate all permutations and combinations

GENERATING ALL POSSIBLE ANSWER

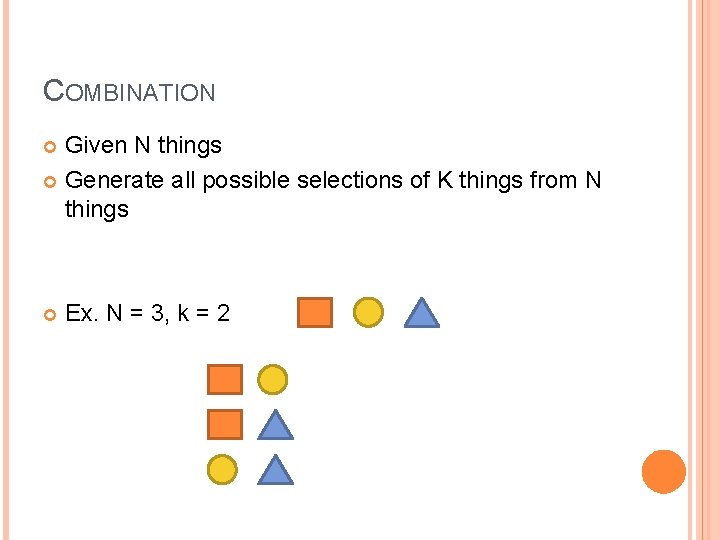
COMBINATION Given N things Generate all possible selections of K things from N things Ex. N = 3, k = 2

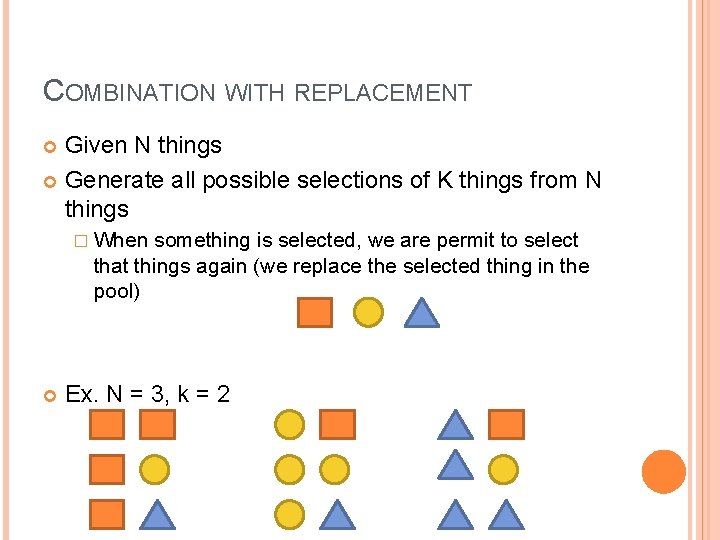
COMBINATION WITH REPLACEMENT Given N things Generate all possible selections of K things from N things � When something is selected, we are permit to select that things again (we replace the selected thing in the pool) Ex. N = 3, k = 2

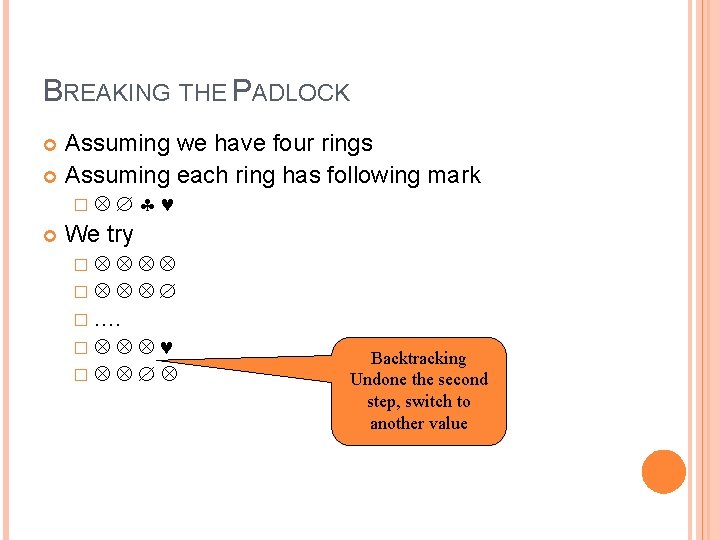
BREAKING THE PADLOCK

BREAKING THE PADLOCK Assuming we have four rings Assuming each ring has following mark � We try � � � …. � � Backtracking Undone the second step, switch to another value

KEY IDEA A problem consists of several similar steps � Choosing a things from the pool We need to remember the things we done so far

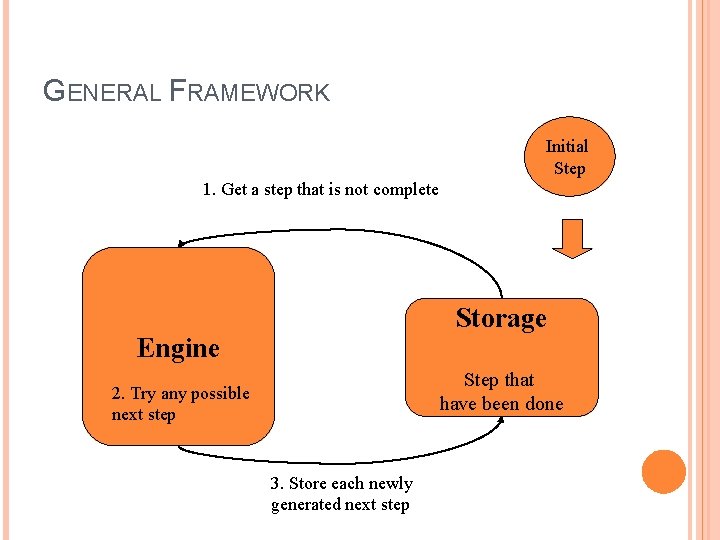
GENERAL FRAMEWORK Initial Step 1. Get a step that is not complete Storage Engine Step that have been done 2. Try any possible next step 3. Store each newly generated next step

COMBINATION Generate all combinations of lock key Represent key by int � =0 � =1 � =2 � =3 Step = sequence of selected symbols � E. g. , ’ 01’ ‘ 0003’

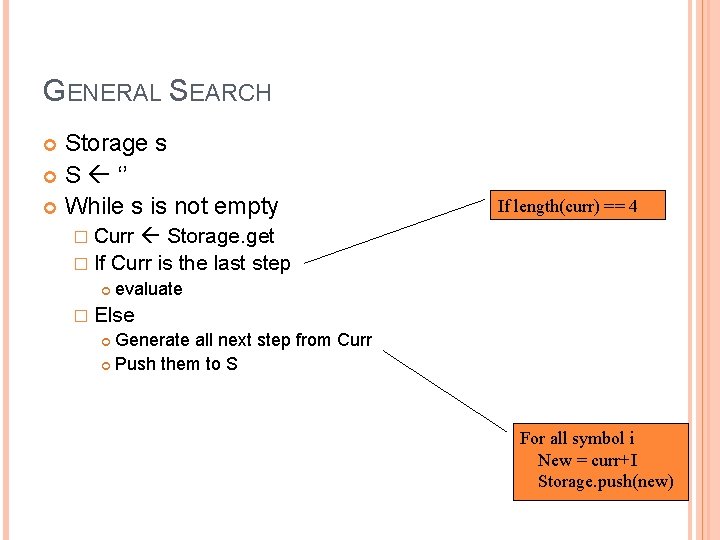
GENERAL SEARCH Storage s S ‘’ While s is not empty If length(curr) == 4 � Curr Storage. get � If Curr is the last step evaluate � Else Generate all next step from Curr Push them to S For all symbol i New = curr+I Storage. push(new)

SEARCH SPACE Set of all admissible solutions E. g. , Combination Padlock � Search space = 0000 4444 For a task with distinct steps it is easy to enumerate the search space with “backtracking” for most of the case, we can do “backtracking”

BACKTRACKING A tool to enumerate the search space Usually using the “stack” to implement the storage � Employ the processor stack � i. e. , using the “recursive” paradigm

COMBINATION EXAMPLE BY BACKTRACKING void backtracking)int step, int *sol ( { if )step < num_step ({ for )int i =0; i < num_symbol; i (++{ sol]step = [i; backtracking)step + 1, sol(; } } else { check)sol(; } } The process automatically remember the step

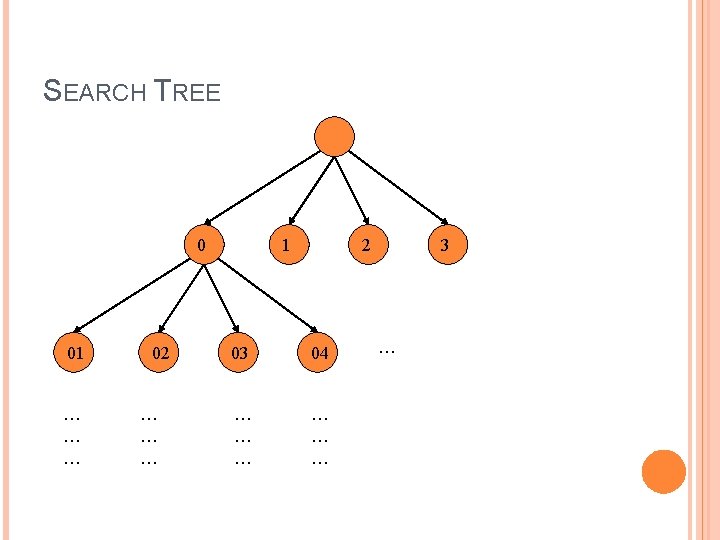
SEARCH TREE Sols in each step � � � � 0 00 0000 check 0001 check 0002 check 0003 check 000 00 0010 check


8 -QUEEN Given a chess board 8 queens X X X X

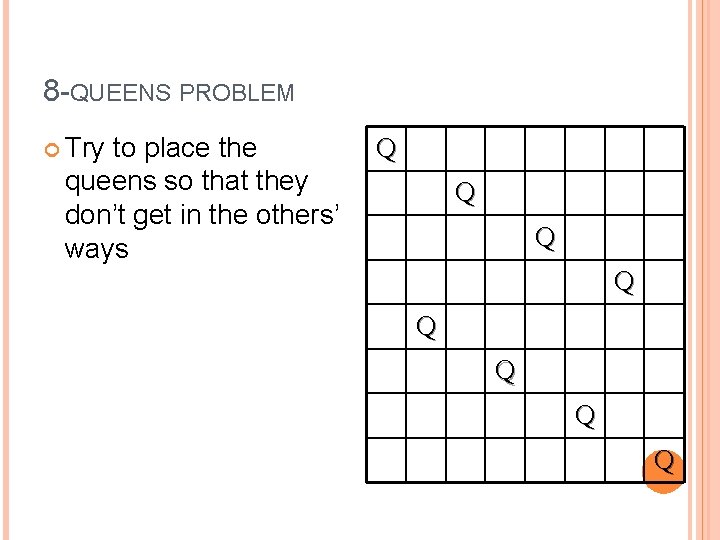
8 -QUEENS PROBLEM Try to place the queens so that they don’t get in the others’ ways Q Q Q Q

SOLVING THE PROBLEM Define the search space � What is the search space of this problem? � How large it is? � Choose an appropriate representation

EXAMPLE Every possible placement of queens � Size: 648 � Representation: a set of queens position E. g. , (1, 1) (1, 2) (2, 5) (4, 1) (1, 2) (3, 4) (8, 8) (7, 6) This includes overlapping placement!!!

EXAMPLE Another representation � Try to exclude overlapping Use combination without replacement � This is a combination Selecting 8 positions out of 64 positions Size: (64)! / (64 – 8)! * 8! � Implementation: overlapping in the “generating next step”, check for

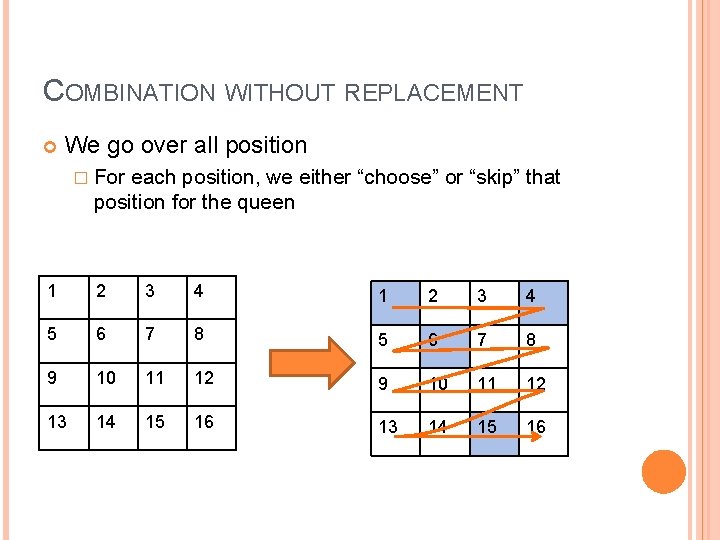
COMBINATION WITHOUT REPLACEMENT We go over all position � For each position, we either “choose” or “skip” that position for the queen 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

COMBINATION WITHOUT REPLACEMENT Mark_on_board is a binary string indicate that whether the position is selected void e_queen(int step, int *mark_on_board) { if (step < 64) { mark_on_board[step] = 0; e_queen(step + 1, mark_on_board); mark_on_board[step] = 1; e_queen(step + 1, mark_on_board); } else { check(mark_on_board); } } Also has to check whether we mark exactly 8 spots

COMBINATION WITHOUT REPLACEMENT The generated mark_on_board includes � 000000 select no position (obviously not the answer) � 111111000000 select 6 positions (obviously not the answer) We must limit our selection to be exactly 4

COMBINATION WITHOUT REPLACEMENT Number of possible 0 void e_queen(int step, int *mark_on_board, int chosen) { if (step < 64) { if ((64 – 8) – (step – chosen) > 0) { mark_on_board[step] = 0; e_queen(step + 1, mark_on_board, chosen); } if (8 - chosen > 0) { mark_on_board[step] = 1; e_queen(step + 1, mark_on_board, chosen+1); } } else { Number of check(mark_on_board); possible 1 } }

EXAMPLE Any better way? For each row, there should be only one queen � Size: 88 � Representation: sequence of columns E. g. , (1, 2, 3, 4, 5, 6, 7, 8)

USING BACKTRACKING? The problem consists of 8 step � Placing each queen We never sure whether the queen we place would lead to a solution Backtracking is an appropriate way

SOLVING THE PROBLEM: ENUMERATING SEARCH SPACE There are eight possible ways in each step There are eight steps Very similar to the combination problem void e_queen(int step, int *queen_pos) { if (step < 8) { for (int i = 0; i < 8; i++) { queen_pos[step] = i; e_queen(step + 1, queen_pos); } } else { check(queen_pos); } }

8 -QUEEN BY PERMUTATION Queen should not be in the same column � The solution should never have any column repeated E. g. , (1, 2, 3, 4, 5, 6, 7, 1) is bad (column collision (1, 1, 3, 4, 5, 6, 7, 5) is bad as well…. (1, 2, 3, 4, 5, 6, 7, 8) is good � There should be no duplicate column index!!!

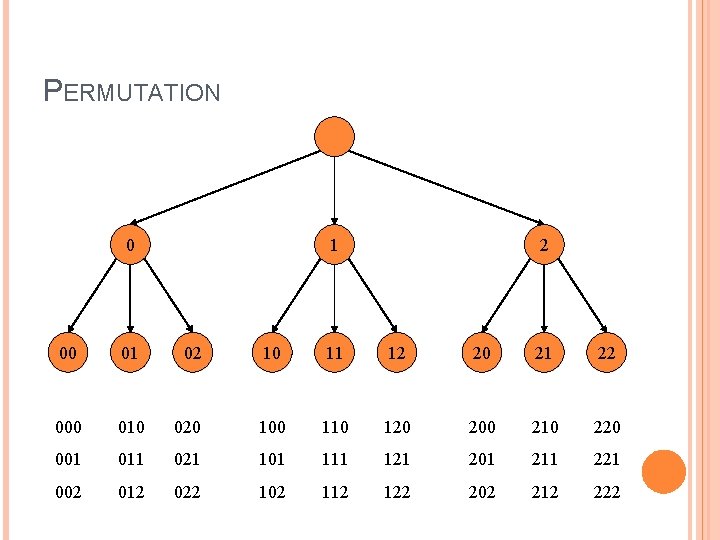
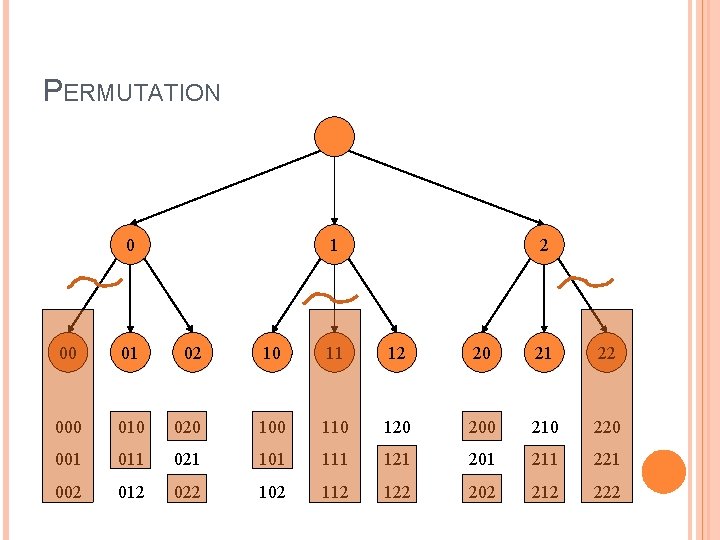
PERMUTATION Given N symbols A permutation is the element arrange in any order � E. g. , 1 2 � Shows 1 2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 … 4 3 2 1 34 For each step, we have to known which one is used

PERMUTATION BY BACKTRACKING The problem consists of several similar steps Special condition � Symbols never repeat How to do? � Easy way: Generate all combination (as done before) Check for ones that symbols do not repeat � Better way: Remember what symbols are used

PERMUTATION void backtracking(int step, int *sol) { if (step < ) { for (int i = 0; i < ; i++) { if not_used(sol, i, step) { sol[step] = i; backtracking(step, sol); } } } else { check(sol); } } Bool not_used(int *sol, int value, int step) { for (int i = 0; i < step; i++) { if (sol[i] == value) return false; } return true; }

PERMUTATION More proper ways void backtracking)int step, int *sol, bool *used ( { if )step < num_step ({ for )int i =0; i < num_symbol; i (++{ if (!used[i]) { used[i] = true; sol[step] = i; backtracking(step, sol, used); used[i] = false; } } } else { check(sol); } }

BACKTRACKING PROBLEMS Given N � Find any sequence of (a 1, a 2, a 3, …) such that a 1 +a 2 + a 3 +… + ak = N ai > 0 ai <= aj for all i < j ai is an integer
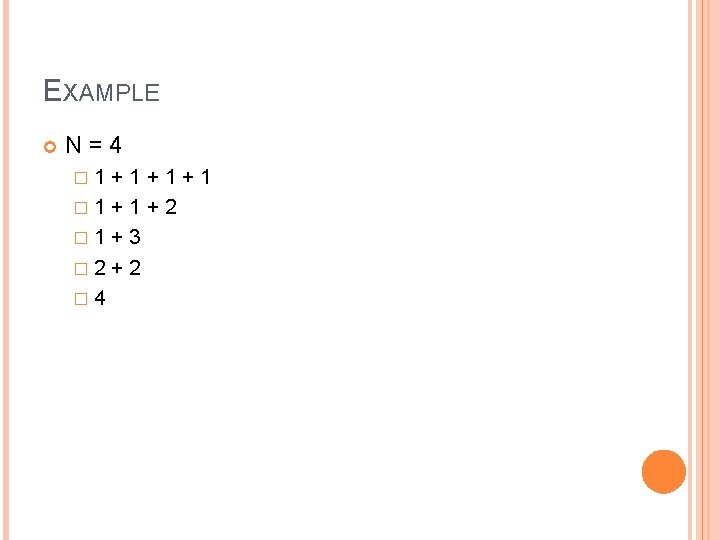
EXAMPLE N=4 � 1 +1+1+1 � 1 + 2 � 1 + 3 � 2 + 2 � 4

SOLVING WITH BACKTRACKING Representation � Array of ai Step � Choosing the next value for ai

BRANCH &BOUND Technique to reduce enumeration

MAIN IDEA We should not enumerate solution that will never produce a solution We have done that!!! � 8 -queens � By naïve combination, we will have to do all 648 But, by each improvement, we further reduce what we have to do

PERMUTATION 0 1 2 00 01 02 10 11 12 20 21 22 000 010 020 100 110 120 200 210 220 001 011 021 101 111 121 201 211 221 002 012 022 102 112 122 202 212 222

PERMUTATION 0 1 2 00 01 02 10 11 12 20 21 22 000 010 020 100 110 120 200 210 220 001 011 021 101 111 121 201 211 221 002 012 022 102 112 122 202 212 222

KEY If we know, at any step, that the solution is not feasible � Then, it is futile to further search along that path

OPTIMIZATION PROBLEM All previous examples are decision problems � Asking whether the solution satisfy the criteria Now, we consider broader set of problem, the optimization problem Example � For all students, find one with maximum height

EVALUATION Representation: x = id of student “goodness evaluation” evaluate(x) For all x in the search space, we have to find one with maximum evaluate(x)

SOLVING OPTIMIZATION PROBLEM Enumerate all possible solution Calculate its value � Remember the max void backtracking)int step, int *sol ( { if )step < num_step ({ for )int i =0; i < num_symbol; i (++{ sol]step = [i; backtracking)step, sol(; } } else { value = evaluate)sol(; if (value > max) remember(value, sol); } }

BRANCH & BOUND IN OPTIMIZATION PROBLEM For many problems, it is possible to assert its goodness even the solution is not complete If we can predict the best value for the remaining step, then we can use that value to “bound” our search

EXAMPLE Assuming that we have 10 steps At step 7, the goodness of the partial solution is X Assuming that we know that the remaining step could not produce a solution better than Y � If we have found a solution better than X+Y We can simply “bound” the search

KEYS We must know the so-called “upper bound” of the remaining step � It should be compute easily

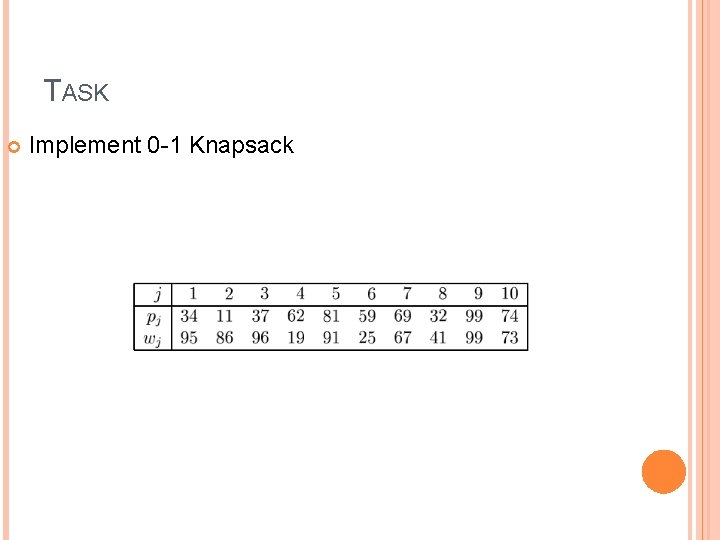
EXAMPLE If we know that this path never bet higher than 13 (which make 10 + 13 < 35) We can neglect it 23 35 2 Let value at this point be 10

KNAPSACK PROBLEM

KNAPSACK PROBLEM Given a sack, able to hold K kg Given a list of objects � Each has a weight and a value Try to pack the object in the sack so that the total value is maximized

VARIATION Rational Knapsack � Object is like a gold bar, we can cut it in to piece with the same value/weight 0 -1 Knapsack � Object cannot be broken, we have to choose to take (1) or leave (0) the object � E. g. K = 50 Objects = (60, 10) (100, 20) (120, 30) Best solution = choose second and third

RATIONAL KNAPSACK Can be solved by greedy Sort object according to value/weight ratio Pick objects by that ratio � If it object is larger than the remaining capacity, just divide

0 -1 KNAPSACK WITH B&B 0 -1 knapsack is very suitable for B&B � We can calculate the goodness of the partial solution Just sum the value of the selected objects � We have fast, good upper bounds (several one) The sum of remaining unselected objects The sum of remaining unselected object that don’t exceed the capacity The solution of the “rational knapsack” of the remaining objects with the remaining capacity

TASK Implement 0 -1 Knapsack