System of Linear Equations Nattee Niparnan LINEAR EQUATIONS







































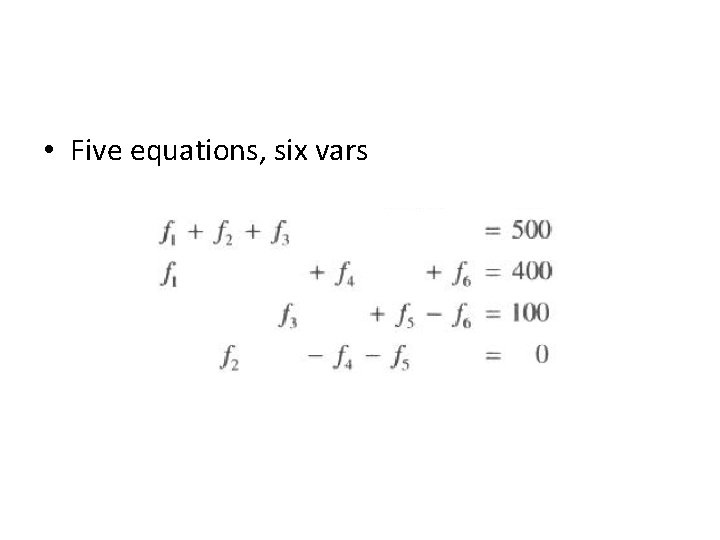
- Slides: 57

System of Linear Equations Nattee Niparnan

LINEAR EQUATIONS

Linear Equation • An Equation – Represent a straight line – Is a “linear equation” in the variable x and y. • General form – ai a real number that is a coefficient of xi – b another number called a constant term

System of a Linear Equation • A collection of several linear equations – In the same variables • What about – A linear equation • in the variables x 1, x 2 and x 3 – Another equation • in the variables x 1, x 2, x 3 and x 4 – Do they form a system of linear equation?

Solution • A linear equation • Has a solution • When • It is called a solution to the system if it is a solution to all equations in the system

Number of Solution • Solution can have – No solution – One solution – Infinite solutions

Example 1 • Show that – For any value of s and t – xi is the solution to the system

Example 1 Solution

Parametric Form • Solution of the system in Equation 1 is described in a – It is given as a function in – It is called a s and t of the system • Every linear equation system having solutions – Can be written in parametric form

Try another one • Solve it using parametric form • In term of x and z • In term of y and z There are several general solutions

Geometrical Point of View • In the case of 2 variables – Each equation is represent a line in 2 D – Every point in the line satisfies the equation • If we have 2 equations – 3 possibilities • Intersect in a point • Intersect as a line • Parallel but not intersect

As a point No intersection As a line

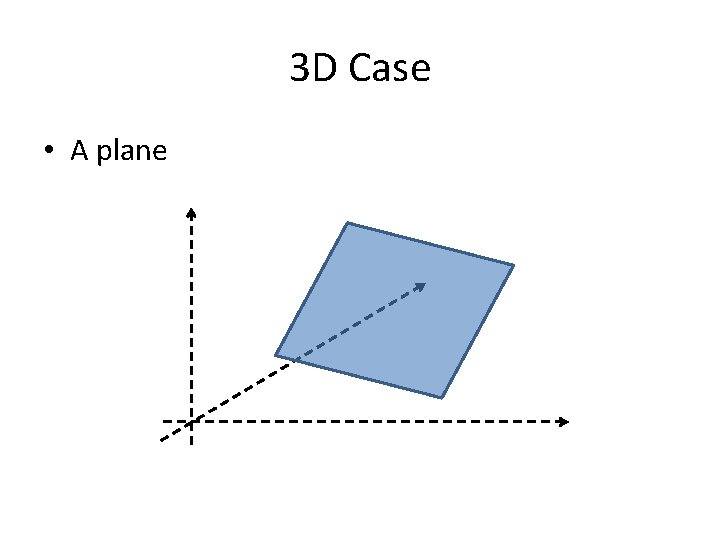
3 D Case • What does represent?

3 D Case • A plane

Higher Space? • Somewhat difficult to imagine – But Linear Algebra will, at least, provides some characteristic for us Cogito, ergo sum I also speak Calculus

MANIPULATING THE SYSTEM

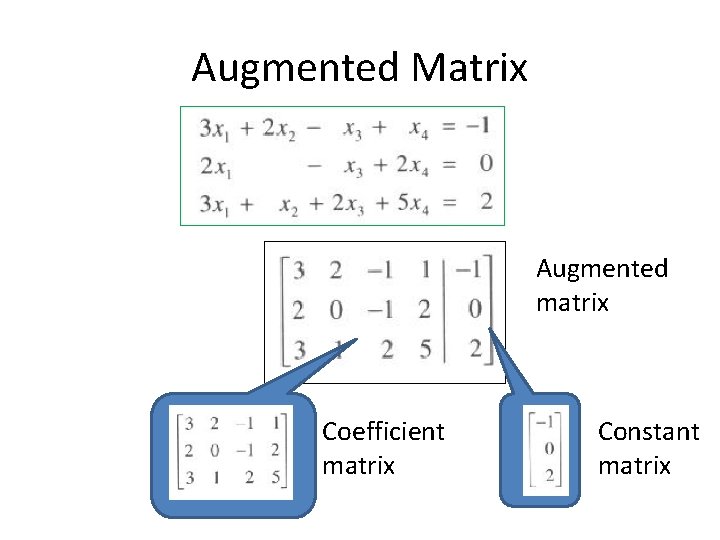
Augmented Matrix Augmented matrix Coefficient matrix Constant matrix

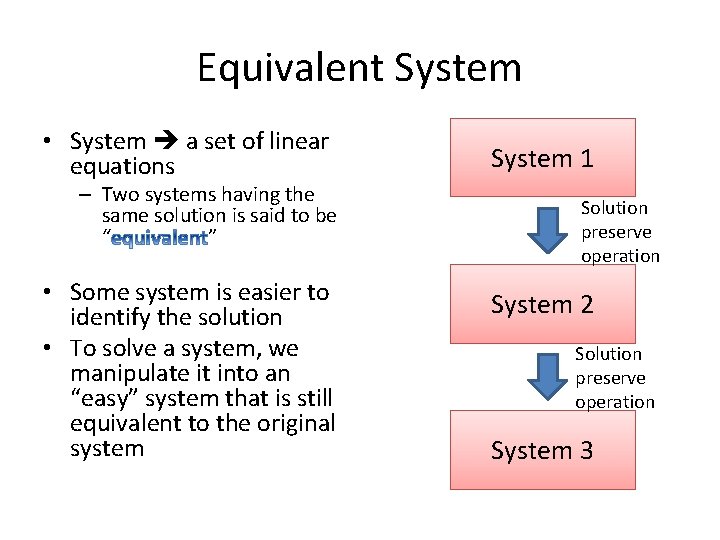
Equivalent System • System a set of linear equations – Two systems having the same solution is said to be “ ” • Some system is easier to identify the solution • To solve a system, we manipulate it into an “easy” system that is still equivalent to the original system System 1 Solution preserve operation System 2 Solution preserve operation System 3

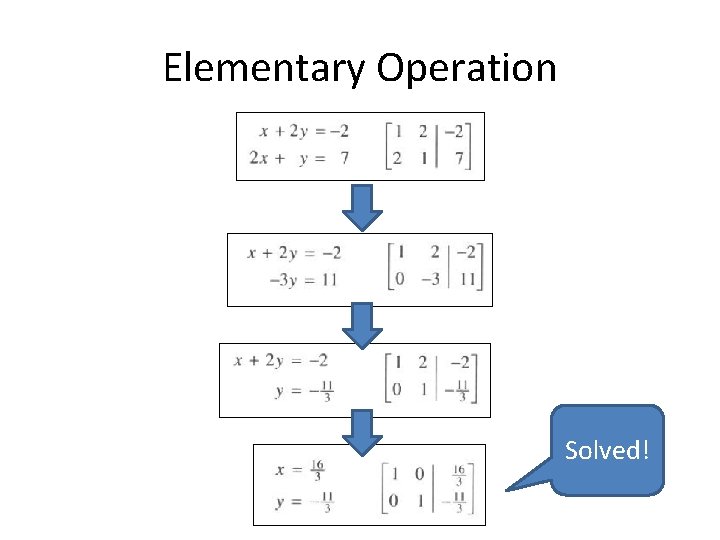
Elementary Operation Solved!

Elementary Operation • Interchange two equations • Multiply one equation with a • Add a multiple of one equation to a equation number

Theorem 1 • Suppose that an elementary operation is performed on a linear equation system – Then, there solution are still the same

Proof

Elementary Row Operation • We don’t really do the elementary operation • We write the system as an augmented matrix and then perform “ ” on that matrix

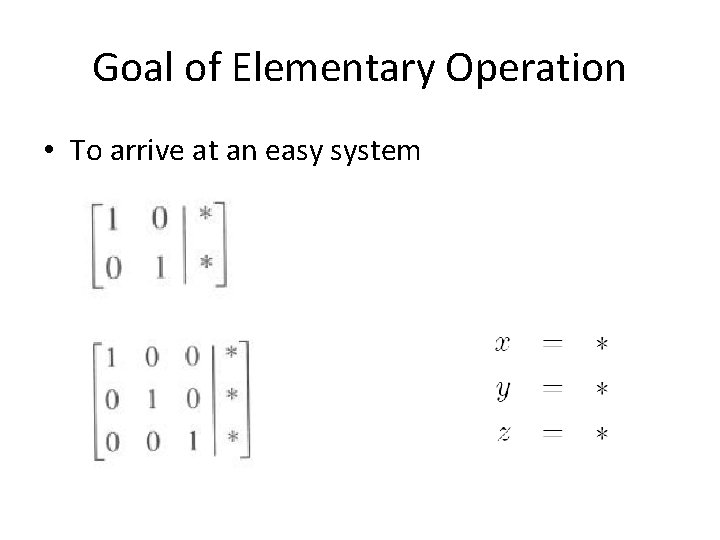
Goal of Elementary Operation • To arrive at an easy system

GAUSSIAN ELIMINATION

Gaussian Elimination • An algorithm that manipulate an augmented matrix into a “nice” augmented matrix

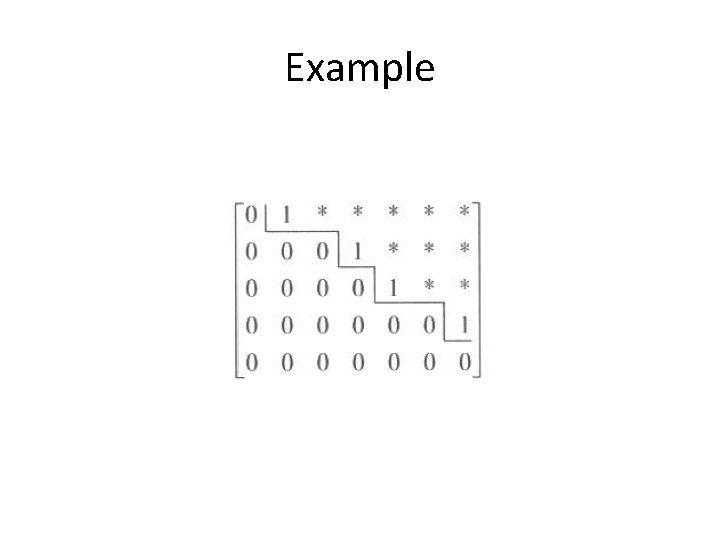
Row Echelon Form • A matrix is in “Row Echelon Form” (called row echelon matrix) if – All zero rows are at the bottom – The first nonzero entry from the left in each nonzero row is 1 • (that 1 is called a leading 1 of that row) – Each leading 1 is to the right of all leading 1’s in the row above it

Example

Echelon? • Diagonal Formation

Reduced Row Echelon • The leading 1 is the only nonzero element in that column row echelon Reduced row echelon

Theorem 2 • Every matrix can be manipulated into a (reduced) row echelon form by a series of elementary row operations

Using (Reduced) Row Echelon Form

Using (Reduced) Row Echelon Form No solution

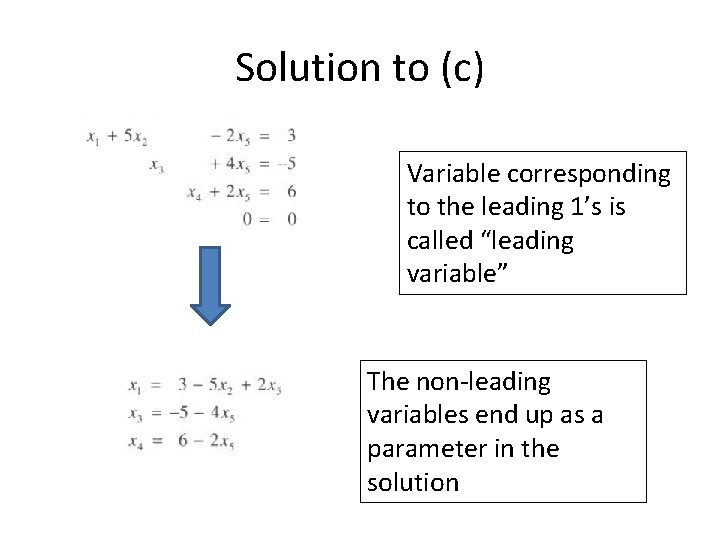
Solution to (c) Variable corresponding to the leading 1’s is called “leading variable” The non-leading variables end up as a parameter in the solution

Gaussian Elimination • If the matrix is all zeroes stop • Find the first column from the left containing a non zero entry (called it A) and move the row having that entry to the top row • Multiply that row by 1/A to create a leading 1 • Subtract multiples of that row from rows below it, making entry in that column to become zero • Repeat the same step from the matrix consists of remaining row

Gauss?

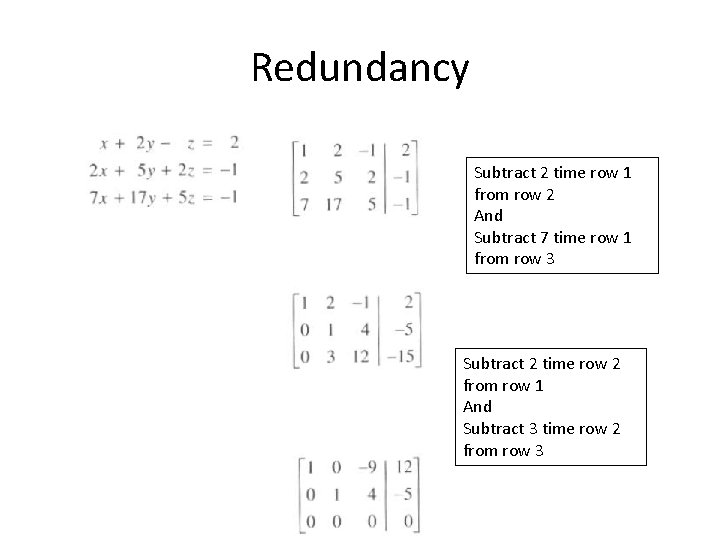
Redundancy Subtract 2 time row 1 from row 2 And Subtract 7 time row 1 from row 3 Subtract 2 time row 2 from row 1 And Subtract 3 time row 2 from row 3

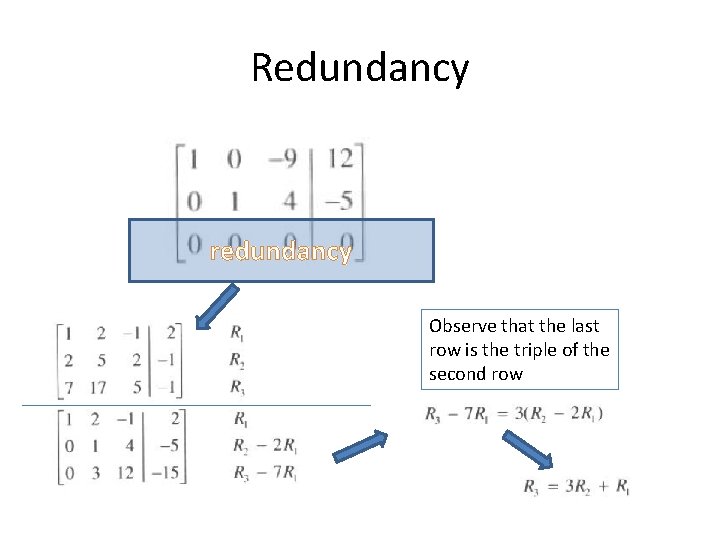
Redundancy redundancy Observe that the last row is the triple of the second row

Back Substitution • Gaussian Elimination brings the matrix into a row echelon form – To create a reduced row echelon form • We need to change step 4 such that it also create zero on the “above” row as well • Usually, that is less efficient • It is better to start from the row echelon form and then use the leading 1 of the bottommost row to create zero

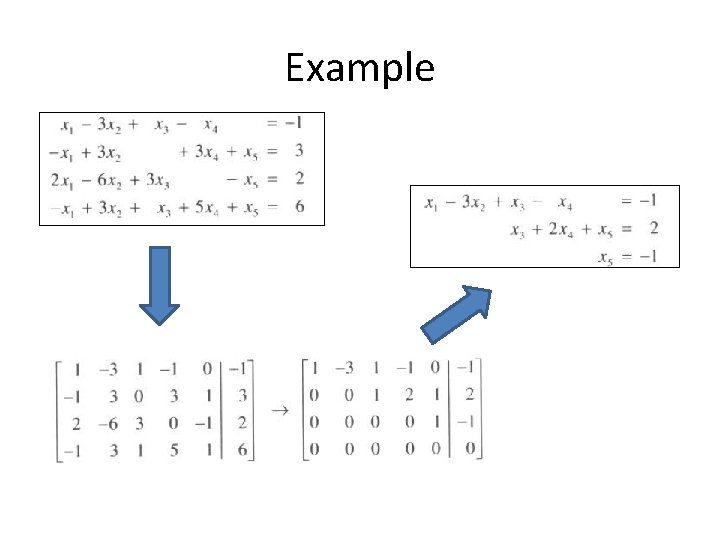
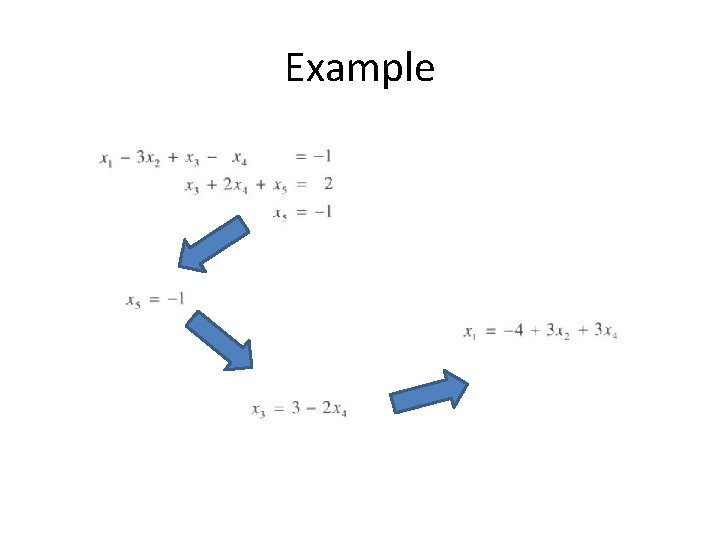
Example

Example

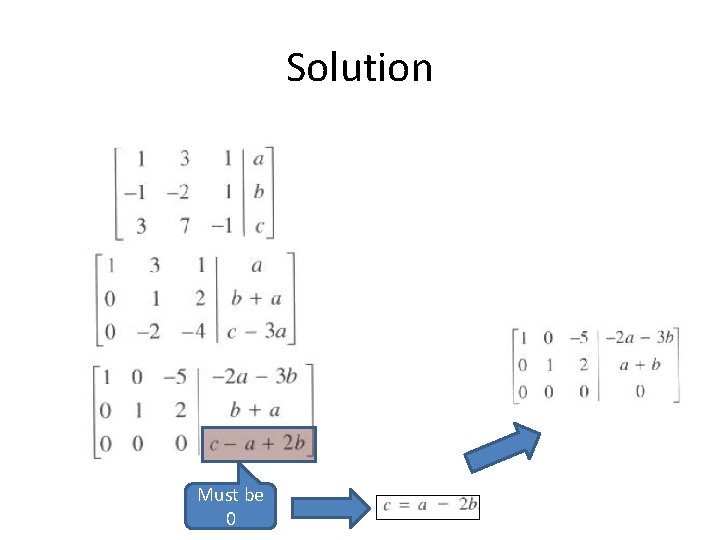
Another Example Try it

Solution Must be 0

Rank • It is (later) shown that, for any matrix A, it has the same “Reduced row echelon form” – Regardless of the elementary row operation performed • But it s not true for “row echelon form” – Different sequence of operations leads to different row echelon matrix • However, the number of leading 1’s is always the same – Will be proved later • Hence, the number of leading 1’s depends on A

Theorem 3 • Suppose a system of equation on variables has a solution, if the rank of the augmented matrix is – the set of the solution involve exactly parameters

Homogeneous Equation When b = 0 What is the solution?

Homogeneous Linear System • Xi = 0 is always a solution to the homogeneous system – It is called “trivial” solution • Any solution having nonzero term is called “nontrivial” solution

Existence of Nontrivial Solution to the homogeneous system • If it has non-leading entry in the row echelon form – The solution can be described as a parameter • Then it has nonzero solution!!! – Nontrivial • When will we have non-leading entry? – When we have more variable than equation

GEOMETRICAL VIEW OF LINEAR EQUATION

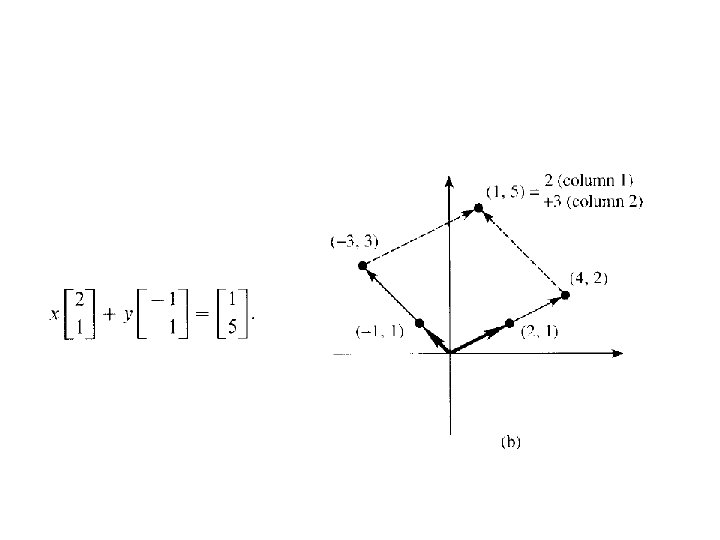
Geometrical Point of View • A system of Linear Equation A line in 2 D

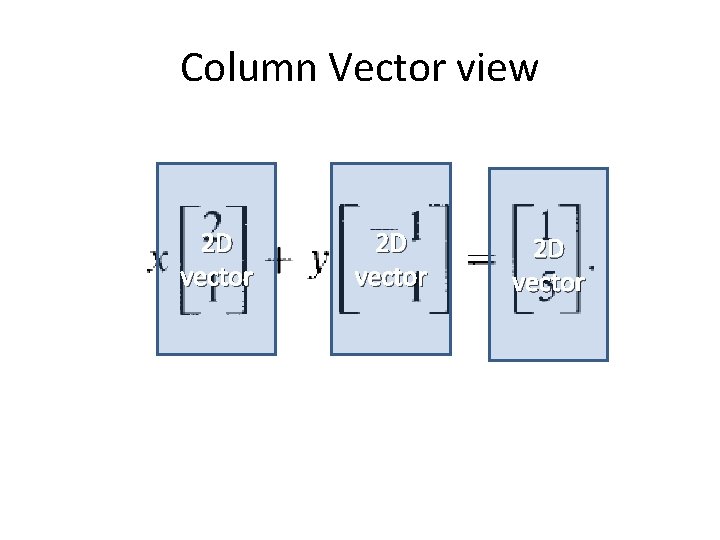
Column Vector view 2 D vector


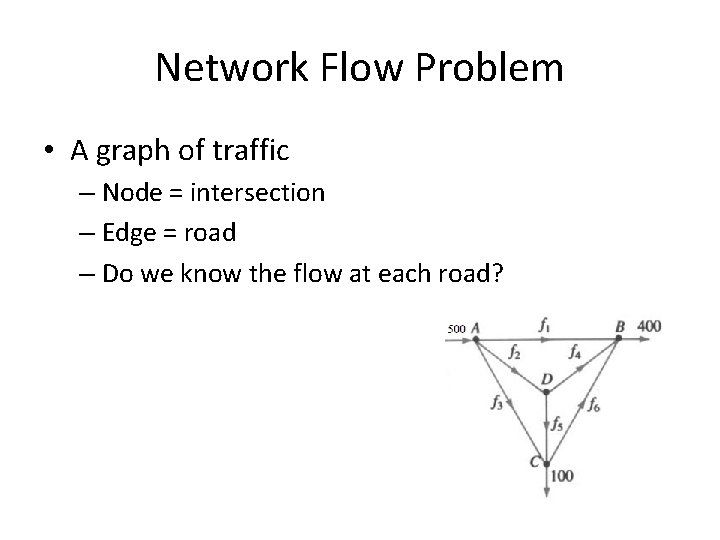
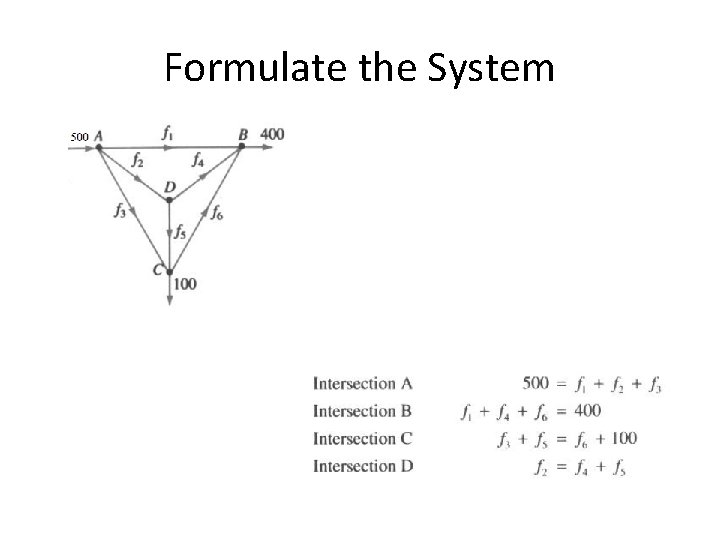
Network Flow Problem • A graph of traffic – Node = intersection – Edge = road – Do we know the flow at each road?

Network Flow Problem • Rules – For each node, traffic in equals traffic out

Formulate the System
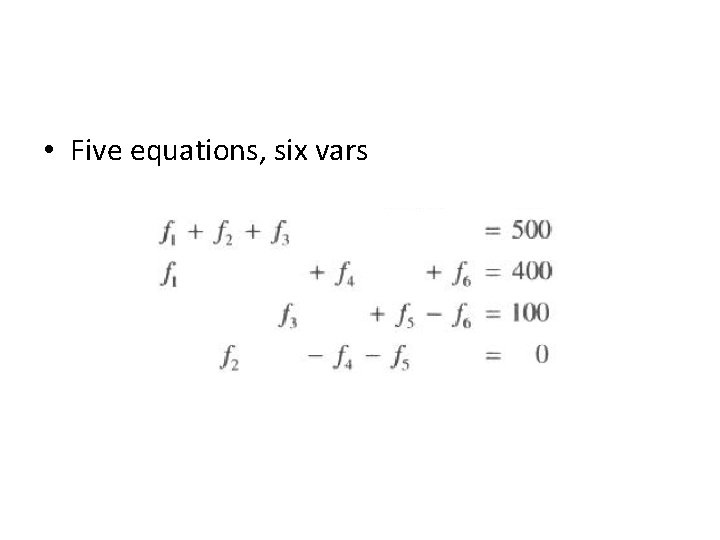
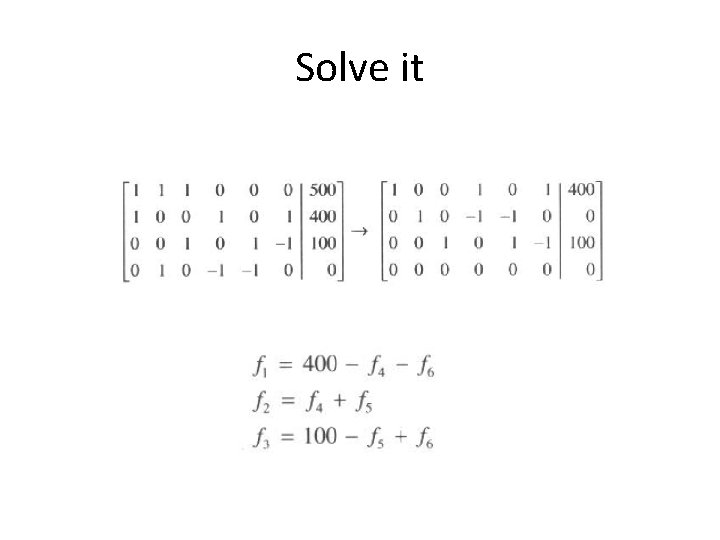
• Five equations, six vars

Solve it
 Armure sergé 2/2
Armure sergé 2/2 Persamaan linier simultan
Persamaan linier simultan Difference between linear and nonlinear analysis
Difference between linear and nonlinear analysis Metode numerik sistem persamaan linear
Metode numerik sistem persamaan linear System of linear equations word problems
System of linear equations word problems System of linear equations with two variables
System of linear equations with two variables Solve systems of equations calculator
Solve systems of equations calculator Equivalent equations examples
Equivalent equations examples System of linear equations
System of linear equations Graph inconsistent
Graph inconsistent Chapter 1 systems of linear equations and matrices
Chapter 1 systems of linear equations and matrices The triangular system of linear equations can be solved by
The triangular system of linear equations can be solved by System of linear and quadratic equations
System of linear and quadratic equations X2+(y-3√×2) 2=1
X2+(y-3√×2) 2=1 Rectangular equations to polar equations
Rectangular equations to polar equations Translate word equations to chemical equations
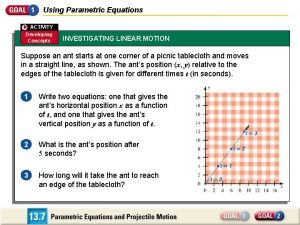
Translate word equations to chemical equations Linear motion equations
Linear motion equations Unit 4 writing linear equations
Unit 4 writing linear equations Reasoning with linear equations
Reasoning with linear equations Vector form
Vector form Standard form
Standard form Gauss jordan method
Gauss jordan method Solving systems of equations
Solving systems of equations Simultaneous linear equations worksheet
Simultaneous linear equations worksheet Linear simultaneous equations
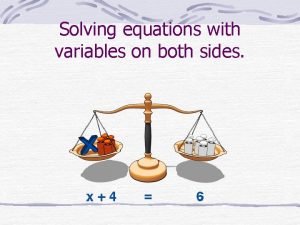
Linear simultaneous equations Solving linear equations with variables on both sides
Solving linear equations with variables on both sides Steps to solving equations with variables on both sides
Steps to solving equations with variables on both sides Solving linear equations with fractions
Solving linear equations with fractions Rotational motion equations
Rotational motion equations Write linear and exponential functions from tables
Write linear and exponential functions from tables Systems of linear equations real world applications
Systems of linear equations real world applications Different forms of linear equations
Different forms of linear equations Solving linear equations: variable on one side
Solving linear equations: variable on one side Constructing equations worksheet
Constructing equations worksheet Learning outcomes of linear equations in one variable
Learning outcomes of linear equations in one variable Table is linear or nonlinear
Table is linear or nonlinear Core focus on linear equations
Core focus on linear equations Characteristics of linear equations
Characteristics of linear equations Y x^2 graph
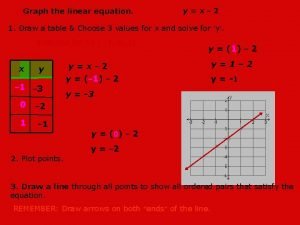
Y x^2 graph Linear equations solving
Linear equations solving First order pde
First order pde Linear equations
Linear equations Euler equation differential equation
Euler equation differential equation Linear motion equations
Linear motion equations Fundamental solutions of linear homogeneous equations
Fundamental solutions of linear homogeneous equations How to get rid of a fraction in a linear equation
How to get rid of a fraction in a linear equation Free fall motion
Free fall motion Writing linear equations from word problems
Writing linear equations from word problems Identifying linear equations
Identifying linear equations Lesson 3 linear equations in x
Lesson 3 linear equations in x Equation with variable on both sides
Equation with variable on both sides Equations with variables on both sides
Equations with variables on both sides Rotational motion equations
Rotational motion equations Converting equations to slope intercept form
Converting equations to slope intercept form Is quadratic equation nonlinear
Is quadratic equation nonlinear Solving equations and inequalities jeopardy
Solving equations and inequalities jeopardy Solving equations with brackets worksheet
Solving equations with brackets worksheet Core focus on linear equations
Core focus on linear equations