Hashing Vishnu Kotrajaras Ph D Nattee Niparnan Ph

Hashing Vishnu Kotrajaras, Ph. D Nattee Niparnan, Ph. D

Flashback Still recall something before midterm?

Recall the previous ADT List, Stack, Queue n BST n AVL n n We wish to do Insert, Delete and Find

Do we happy with AVL tree? n We want something FASTER!!! n Possible with “hashing”

Overview What is hash?

Hashing property Insert O(1( n Delete O(1( n Find O(1( n n Lacks order, traversal

Hashing Idea n What happen if all possible data is the date of the month? n Post Office analogy n Addressing!!!

Hash Table (storage( n Key (address( n And possibly the Value (things to store( n

Realization of Hash Table Put it into a practical use

What is the problem? n What if the data is not only 1 – 31? n What if the data is not a number?

Hash function n Mash key into something else

Hash function n We use it to try to distribute values evenly throughout our table. We may use: n Key number % table. Size n But if table. Size is 10, 20, 30, …we cannot use this function. n n What if keys are Strings? Let’s see some example.

Hash function (1 st example) n Sum the ASCII values of all alphabets public static int hash(String key, int table. Size){ int hash. Val = 0; for(int i =0; i<key. length(); i++) hash. Val += key. char. At(i); return hash. Val%table. Size; }

n The method in the last page is not good if the table is large: n n Whet if each key is short (e. g. 8 alphabets? ) An ASCII normally has a maximum value of 127. n n Therefore the sum of all 8 alphabets will not exceed 127*8. If the table is big, data will not be distributed evenly. The 10, 000 th member Indices will concentrate at the front.

Hash function (2 nd example) Assume we have a big table, and each key is made from at least 3 random alphabets. n We look at the first 3 alphabets only. n public static int hash(String key, int table. Size){ return (key. char. At(0) +27*key. char. At(1) +729* key. char. AT(2))%table. Size; } All alphabets, including space 27*27 This distributes well in a table of size 10000. (10007 is the first prime after 10000, we will use this number. You will see why).

n Wait, any actual key will never be random like this: n There will be a lot of repetition.

Hash function (3 rd example( We calculate a polynomial function of 37, using Horner’s Rule. n We can calculate k 0 + 37 k 1+ 37*37 k 2 by using [(k 2*37)+k 1]*37 +k 0 Horner rule is to repeat this -> n times. In fact, it is a calculation of: n

public static int hash(String key, int table. Size){ int hash. Val = 0; for(int i =0; i<key. length(); i++) hash. Val= 37*hash. Val+key. char. At(i); hash. Val %= table. Size; if(hash. Val<0) hash. Val += table. Size; Possible overflow return hash. Val; }

What is “GOOD” hash function? Low cost n Determinism n Uniformity n Variable Range n Injective n n Perfect hash function?

Side Note e. Mule, Bit. Torrent, all P 2 P MD 5

Still More Problem Collision

Collision Resolution n Separate Chaining n n Toolbox analogy Open addressing n Library shelf analogy

Separate Chaining n Try to put it into the same position n Use another “Data Structure”

Fixing collision: separate chaining n n n Store repeated elements in a linked list. If you want to search for an element, use hash function, then search in the list given by that hash function. If you want to insert an element, n use hash function to find a list to put that element in. n After that, check the list to see whether it already contains the element. If the list does not have that element then insert the element at the front. n Statistically, a newly inserted element is often accessed again soon after the insertion.

Code for an object that has a hash function. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. public interface Hashable { /** * Compute a hash function for this object. * @param table. Size the hash table size. * @return (deterministically) a number between * 0 and table. Size-1, distributed equitably. */ int hash( int table. Size ); }

How we use a Hashable object. Public class Student implements Hashable{ private String name; private double number; private int year; public int hash(int table. Size){ return Separate. Chaining. Hash. Table. hash(name, table. Size); } static method from our Hash. Table class. public boolean equals(Object rhs){ return name. equals(((Student)rhs). name); } }

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. public class Separate. Chaining. Hash. Table { /** * Construct the hash table. */ public Separate. Chaining. Hash. Table( ) { this( DEFAULT_TABLE_SIZE ); } /** * Construct the hash table. * @param size approximate table size. */ public Separate. Chaining. Hash. Table( int size ) { the. Lists = new Linked. List[ next. Prime( size ) ]; for( int i = 0; i < the. Lists. length; i++ ) the. Lists[ i ] = new Linked. List( ); }

20. 21. 22. 23. 24. 25. 26. 27. 28. /** * Insert into the hash table. If the item is * already present, then do nothing. * @param x the item to insert. */ We use Student public void insert( Hashable x ) { Linked. List which. List = the. Lists[ x. hash( the. Lists. length ) ]; Linked. List. Itr itr = which. List. find( x ); if( itr. is. Past. End( ) ) which. List. insert( x, which. List. zeroth( ) ); 29. 30. 31. } 32. /** * Remove from the hash table. * @param x the item to remove. */ public void remove( Hashable x ) { the. Lists[ x. hash( the. Lists. length ) ]. remove( x ); } 33. 34. 35. 36. 37. 38. 39. here

40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. /** * Find an item in the hash table. * @param x the item to search for. * @return the matching item, or null if not found. */ public Hashable find( Hashable x ) { return (Hashable)the. Lists[ x. hash( the. Lists. length ) ]. find( x ). retrieve( ); } /** * Make the hash table logically empty. */ public void make. Empty( ) { for( int i = 0; i < the. Lists. length; i++ ) the. Lists[ i ]. make. Empty( ); }

57. 58. 59. 60. 61. 62. 63. 64. 65. /** * A hash routine for String objects. * @param key the String to hash. * @param table. Size the size of the hash table. * @return the hash value. */ public static int hash( String key, int table. Size ) { int hash. Val = 0; for( int i = 0; i < key. length( ); i++ ) hash. Val = 37 * hash. Val + key. char. At( i ); 66. 67. 70. hash. Val %= table. Size; if( hash. Val < 0 ) hash. Val += table. Size; 71. return hash. Val; 68. 69. 72. }

73. private static final int DEFAULT_TABLE_SIZE = 101; 74. /** The array of Lists. */ private Linked. List [ ] the. Lists; 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. /** * Internal method to find a prime number at least as large as n. * @param n the starting number (must be positive). * @return a prime number larger than or equal to n. */ private static int next. Prime( int n ) { if( n % 2 == 0 ) n++; 86. for( ; !is. Prime( n ); n += 2 ) ; 87. return n; 85. 88. }

89. 90. 91. 92. 93. 94. 95. 96. 97. 98. /** * Internal method to test if a number is prime. * Not an efficient algorithm. * @param n the number to test. * @return the result of the test. */ private static boolean is. Prime( int n ) { if( n == 2 || n == 3 ) return true; if( n == 1 || n % 2 == 0 ) return false; 99. 100. 103. for( int i = 3; i * i <= n; i += 2 ) if( n % i == 0 ) return false; 104. return true; 101. 102. 105. }

// Simple main public static void main( String [ ] args ) { Separate. Chaining. Hash. Table H = new Separate. Chaining. Hash. Table( ); 106. 107. 108. 109. 111. final int NUMS = 4000; final int GAP = 37; 112. System. out. println( "Checking. . . (no more output means success)" ); 113. for( int i = GAP; i != 0; i = ( i + GAP ) % NUMS ) H. insert( new My. Integer( i ) ); for( int i = 1; i < NUMS; i+= 2 ) H. remove( new My. Integer( i ) ); 110. 114. 115. 116. for( int i = 2; i < NUMS; i+=2 ) if( ((My. Integer)(H. find( new My. Integer( i ) ))). int. Value( ) != i ) System. out. println( "Find fails " + i ); 117. 118. 119. for( int i = 1; i < NUMS; i+=2 ) { if( H. find( new My. Integer( i ) ) != null ) System. out. println( "OOPS!!! " + i ); } 120. 121. 122. 123. 124. } 125. 126. }

Separate Chaining : More variation n Can we use BST instead? AVL? n B-Tree? n

Some Analysis n Load factor n It is an average length of linked list. Search time = time to do hashing + time to search list = constant + time to search list n Unsuccessful search Search time == average list length == load factor

n Successful search n n In a list that we will search, there is one node that contains an object that we want to find. There are other nodes too (0 or more). in a table, if we have N members, distributed into M lists. n n n n There are N-1 nodes that do not have what we want. If we distribute these nodes evenly among the lists. Each list will have (N-1)/M nodes. = lambda- (1/M) = lambda, because M is large. On average, half the list will be searched before we find what we want. That is, lambda/2 steps will be executed. Therefore the average time to find the required element is 1 + (lambda/2) steps. The table. Size is not important. What really matters is the load factor.

Open Addressing n Try to use another slot n n “Probing” Try h 0(x), h 1(x), … hi(x)=[hash(x)+f(i)]%table. Size, f(0)=0 n “i” is the collision count n n Use no extra space n Load factor is very important

Open Addressing Technique Linear probing n Quadratic probing n Double hashing n

Fixing collision by using Open addressing No list. n If there is a collision, then keep calculating a new index until an empty slot is found. n The new index is at h 0(x), h 1(x), … n hi(x)=[hash(x)+f(i)]%table. Size, f(0)=0 n n Every data must be put into our table. Therefore the table must be large enough to distribute data. n Load factor <=0. 5

Open addressing: linear probing F is a linear function of i. n Normally we have -> f(i)=i n It is “looking ahead one slot at a time. ” n n This may take time. There will be consecutive filled slots, called primary clustering. If a new collision takes place, it will take some time before we can find another empty slot.

Open addressing: quadratic probing n There is no primary clustering by this method. n We usually have -> f(i)=i 2 n hi(x)=[hash(x)+f(i)]%table. Size a if b collides with a, we add 12 to find a new empty slot. If c also collides with a, we add 12 to find b. We need to go further by adding 22 instead.

However, if our table is more than half full or the table. Size is not prime, this method does not guarantee an empty slot. n But if the table is not yet half full and the table. Size is prime, it is proven that we can always find an empty slot for a new value. n

Proof Let the table. Size be a prime number greater Be 2 empty slot positions. than 3. n Let (h(x)+i 2) mod table. Size n (h(x)+j 2) mod table. Size n Prove by contradiction n n Assume both positions are the same and i !=j.

n n n i-j =0 is impossible because we assumed they are not equal. i+j=0 is also impossible, Therefore our assumption that the two positions are the same is wrong. Thus the two positions are always different. So there is always a slot for a new value, if the table is not yet half full and the table. Size is prime.

Why prime? If not, the number of available slots will greatly reduce. n Example: table. Size == 16. Assume a normal hashing gives index ==0. (quadratic probing( n 12 42 72 22 62 32 52 You can see that they fall in the same positions.

Deleting in open addressing

Open addressing implementation class Hash. Entry { Hashable element; // the element boolean is. Active; // false means -> deleted public Hash. Entry( Hashable e ){ this( e, true ); } public Hash. Entry( Hashable e, boolean i ){ element = e; is. Active = i; } }

1. 2. 3. 4. 5. public class Quadratic. Probing. Hash. Table{ private static final int DEFAULT_TABLE_SIZE = 11; /** The array of elements. */ private Hash. Entry [ ] array; // The array of elements private int current. Size; // The number of occupied cells 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. public Quadratic. Probing. Hash. Table( ){ this( DEFAULT_TABLE_SIZE ); } null active nonactive /** * Construct the hash table. * @param size the approximate initial size. */ public Quadratic. Probing. Hash. Table( int size ){ allocate. Array( size ); make. Empty( ); }

18. /** 19. * Internal method to allocate array. * @param array. Size the size of the array. */ private void allocate. Array( int array. Size ){ array = new Hash. Entry[ array. Size ]; } 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. /** * Make the hash table logically empty. */ public void make. Empty( ){ current. Size = 0; for( int i = 0; i < array. length; i++ ) array[ i ] = null; }

33. 34. 35. 36. 37. 38. 39. 40. /** * Return true if current. Pos exists and is active. * @param current. Pos the result of a call to find. Pos. * @return true if current. Pos is active. */ private boolean is. Active( int current. Pos ){ return array[ current. Pos ] != null && array[ current. Pos ]. is. Active; }

48. /** * Method that performs quadratic probing resolution. * @param x the item to search for. * @return the position where the search terminates. */ private int find. Pos( Hashable x ) { f(i)=i 2=f(i-1)+2 i-1 /* 1*/ int collision. Num = 0; /* 2*/ int current. Pos = x. hash( array. length ); 49. /* 3*/ 41. 42. 43. 44. 45. 46. 47. while( array[ current. Pos ] != null && !array[ current. Pos ]. element. equals( x ) ){ current. Pos += 2 * ++collision. Num - 1; // Compute ith probe if( current. Pos >= array. length ) // Implement the mod current. Pos -= array. length; 50. 51. 52. 53. /* 4*/ /* 5*/ /* 6*/ } 54. 55. 56. /* 7*/ } return current. Pos;

57. 58. 59. 60. 61. 62. 63. 64. 65. /** * Find an item in the hash table. * @param x the item to search for. * @return the matching item. */ public Hashable find( Hashable x ){ int current. Pos = find. Pos( x ); return is. Active( current. Pos ) ? array[ current. Pos ]. element : null; }

76. /** * Insert into the hash table. If the item is * already present, do nothing. * @param x the item to insert. */ public void insert( Hashable x ) { // Insert x as active int current. Pos = find. Pos( x ); if( is. Active( current. Pos ) ) return; //x is already inside, so do nothing 77. array[ current. Pos ] = new Hash. Entry( x, true ); 78. // Rehash; see Section 5. 5 if( ++current. Size > array. length / 2 ) rehash( ); 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 79. 80. 81. }

97. 98. 99. 100. 101. 102. 103. 104. 105. 106. /** * Remove from the hash table. * @param x the item to remove. */ public void remove( Hashable x ) { int current. Pos = find. Pos( x ); if( is. Active( current. Pos ) ) array[ current. Pos ]. is. Active = false; } hash, next. Prime, is. Prime are the same as before.

rehashing n Rehash can be done due to 3 situations. Do it immediately when the table is half full. n Do it when our insert starts to fail. n Do it when a load factor is up to some value (Does not have to be 0. 5) n n Do not forget that the more the load factor value, the more difficult it is to insert.

82. 83. 84. 85. 86. 87. /** * Expand the hash table. */ private void rehash( ) { Hash. Entry [ ] old. Array = array; O(N) because there are N members to be rehashed. This is not done often because the table has to be half filled first. // Create a new double-sized, empty table allocate. Array( next. Prime( 2 * old. Array. length ) ); current. Size = 0; 88. 89. 90. 94. // Copy table over for( int i = 0; i < old. Array. length; i++ ) if( old. Array[ i ] != null && old. Array[ i ]. is. Active ) insert( old. Array[ i ]. element ); 95. return; 91. 92. 93. 96. } recalculate index because this is a new array.

Downside of quadratic probing Secondary clustering n Fixed by double hashing: n f(i) = i*hash 2(x) n We find hash 2(x), 2 *hash 2(x), …and so on. n n Must be careful when choosing a function. If our array has 9 slots and hash 2(x) = x%9 -> if we insert 99, we will always get 0. n hash 2(x) must not give 0. n

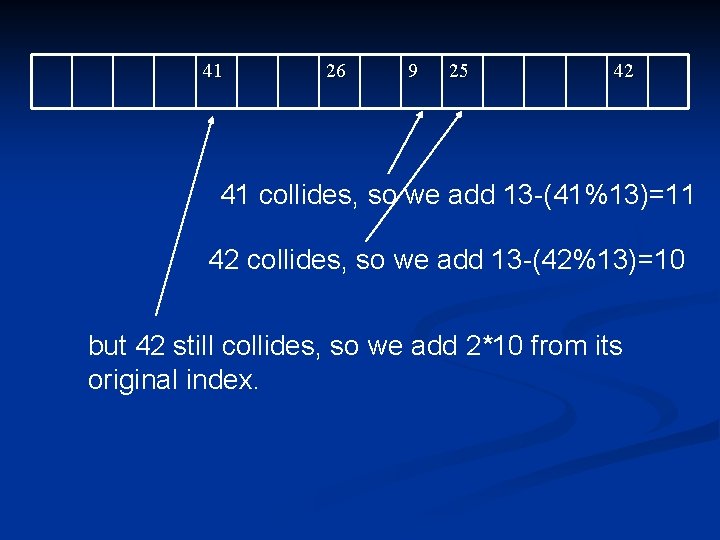
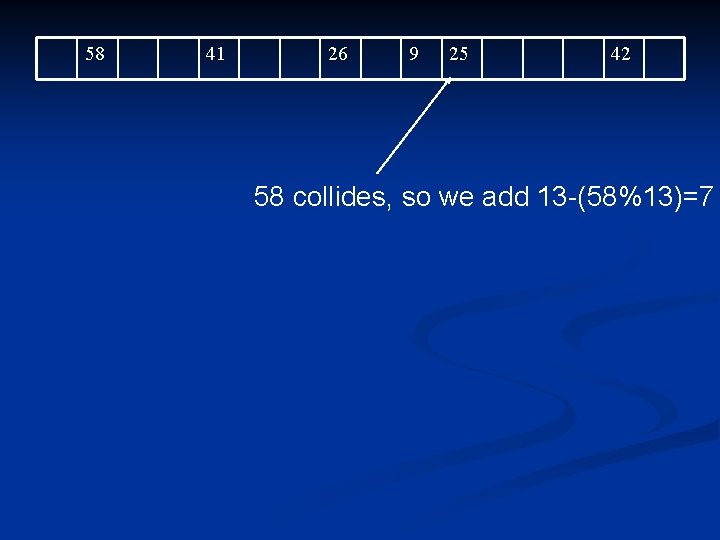
Example of hash 2 Assume hash(x) = x%table. Size n hash 2(x)=R-(x%R) , R is prime and R< table. Size n Let our table. Size be 16. We insert 9, 25, 26, 41, 42, 58 respectively. n 26 9 25 25 collides, so we add 13 -(25%13)=1 26 collides, so we add 13 -(26%13)=13

41 26 9 25 42 41 collides, so we add 13 -(41%13)=11 42 collides, so we add 13 -(42%13)=10 but 42 still collides, so we add 2*10 from its original index.

58 41 26 9 25 42 58 collides, so we add 13 -(58%13)=7