Lecture 5 Strongly Connected Components 2004 SDU 1

Lecture 5 -Strongly Connected Components 2004 SDU 1

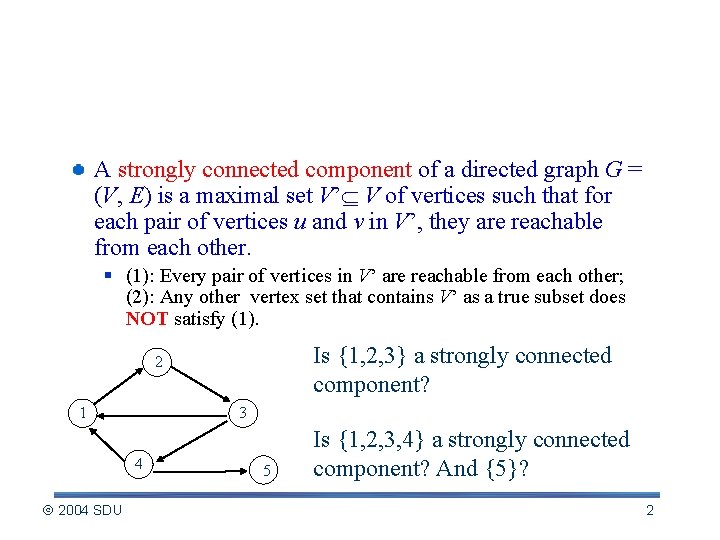
Strongly Connected Components A strongly connected component of a directed graph G = (V, E) is a maximal set V’ V of vertices such that for each pair of vertices u and v in V’, they are reachable from each other. § (1): Every pair of vertices in V’ are reachable from each other; (2): Any other vertex set that contains V’ as a true subset does NOT satisfy (1). Is {1, 2, 3} a strongly connected component? 2 1 3 4 2004 SDU 5 Is {1, 2, 3, 4} a strongly connected component? And {5}? 2

The Strongly Connected Components Decomposition Problem The problem: § Input: A directed graph G = (V, E). § Output: All the strongly connected components of G. In practice, many algorithms that work with directed graphs begin with a strongly connected components decomposition. 2004 SDU 3

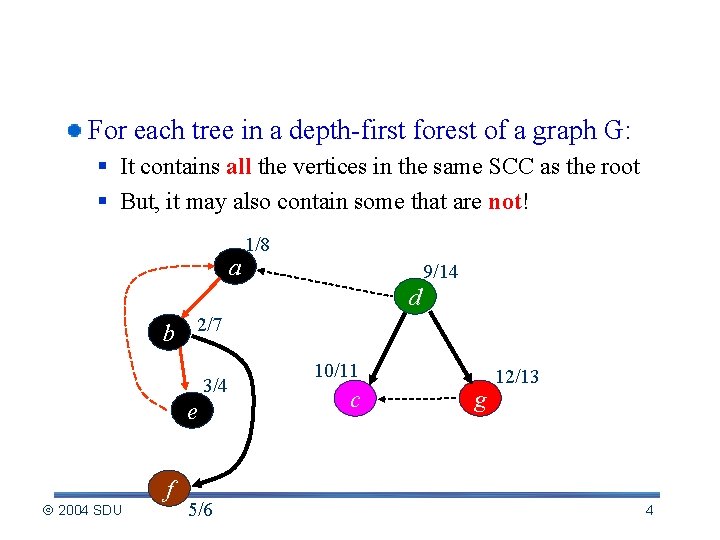
Observation For each tree in a depth-first forest of a graph G: § It contains all the vertices in the same SCC as the root § But, it may also contain some that are not! a 1/8 9/14 d b 2/7 3/4 e 2004 SDU f 5/6 10/11 c g 12/13 4

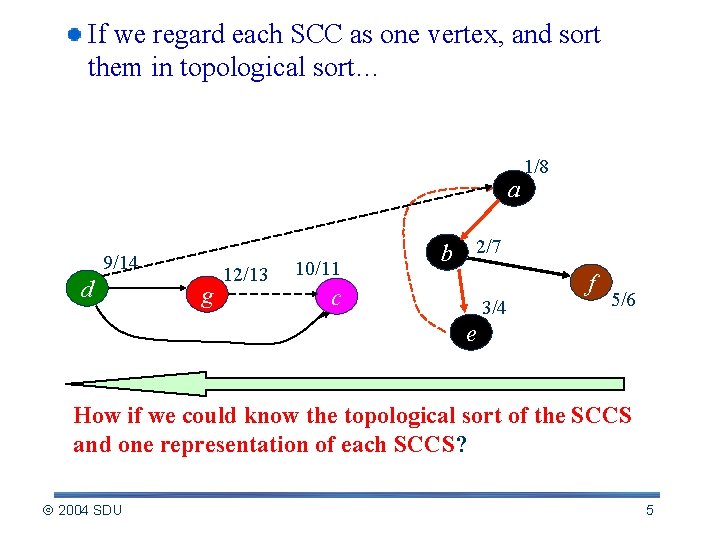
If we regard each SCC as one vertex, and sort them in topological sort… a 9/14 d g 12/13 10/11 1/8 b 2/7 f c 3/4 5/6 e How if we could know the topological sort of the SCCS and one representation of each SCCS? 2004 SDU 5

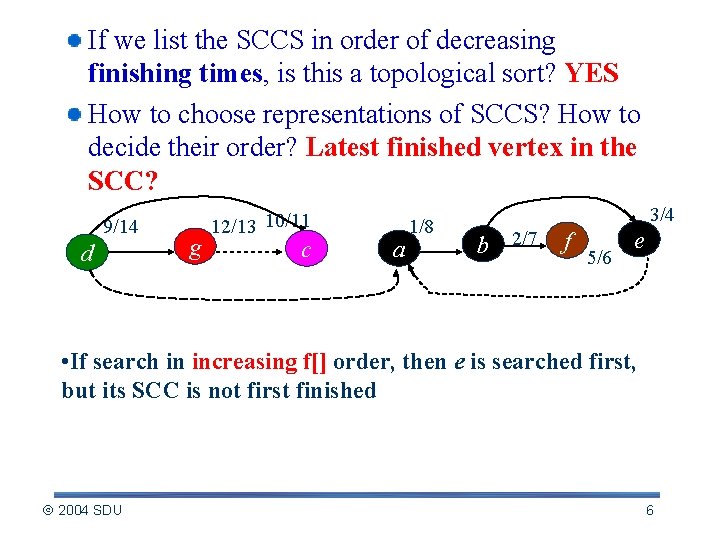
If we list the SCCS in order of decreasing finishing times, is this a topological sort? YES How to choose representations of SCCS? How to decide their order? Latest finished vertex in the SCC? 9/14 d g 12/13 10/11 c a 1/8 3/4 b 2/7 f 5/6 e • If search in increasing f[] order, then e is searched first, but its SCC is not first finished 2004 SDU 6

How if reorder the edges and search in decreasing f[] order? 9/14 d g 12/13 10/11 c a 1/8 b 2/7 f 5/6 3/4 e 2004 SDU 7

Observations Given a directed graph G = (V, E) § G and GT have exactly the same strongly connected components, that is, § u and v are reachable from each other in G if and only if they are reachable from each other in GT. § Note: GT is the transpose of G, i. e. , GT=(V, ET), where ET={(v, u)| (u, v) E}. Given an adjacency-list representation of G, the time to create GT is (V + E). 2004 SDU 8

The Component Graph of G The component graph GSCC = (VSCC, ESCC) of a directed graph G = (V, E) is defined as follows: § Suppose that G has strongly connected components C 1, C 2, …, Ck: – The vertex set VSCC = {vi | vi corresponds to component Ci of G} – The edge set ESCC = {(vi, vj) | G contains a directed edge (x, y) for some x Ci and some y Cj} If we know all the SCCs of G, how can we construct the component graph GSCC? 2004 SDU 9

A Key Property of GSCC The component graph GSCC = (VSCC, ESCC) is a directed acyclic graph. (Lemma 22. 13) § Proof. Suppose for the contrary that GSCC is cyclic, that is, there exist two vertices u, v VSCC such that u and v are reachable from each other. Suppose u and v represent the two strongly connected components Cu and Cv of G, then vertices in Cu and Cv are reachable from each other, which contradicts with the definition of strongly connected component. 2004 SDU 10

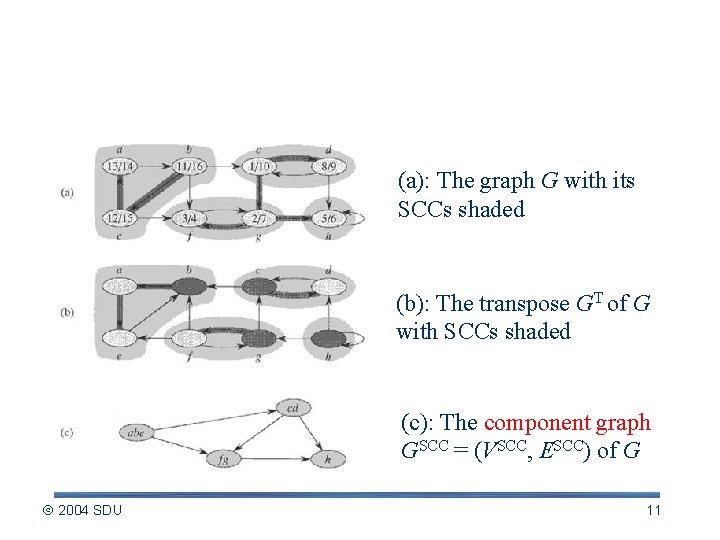
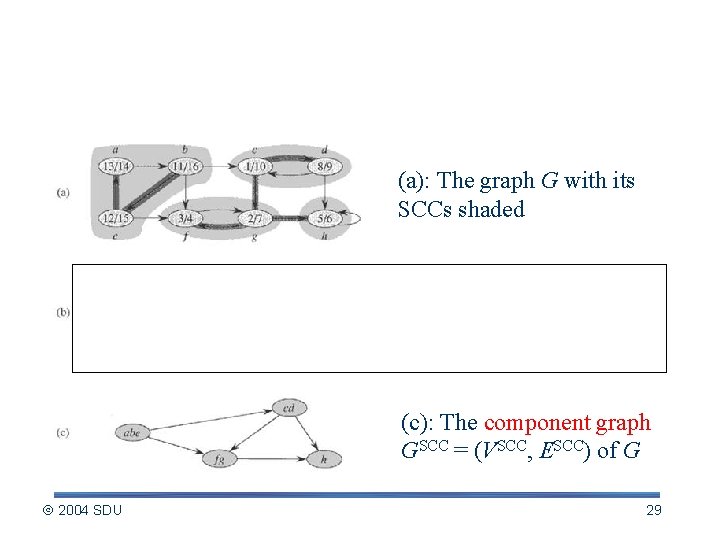
An Example (a): The graph G with its SCCs shaded (b): The transpose GT of G with SCCs shaded (c): The component graph GSCC = (VSCC, ESCC) of G 2004 SDU 11

The Algorithm Time Complexity: line 1, line 2, line 3: (V + E) line 4: O(V) 2004 SDU How? 12

Notations If U V, define § d[U] = minu U{d[u]}, the discovery time of vertex set U, that is, the earliest discovery time of any vertex in U; § f[U] = maxu U{f[u]}, the finishing time of vertex set U, that is, the latest finishing time of any vertex in U. 2004 SDU 13

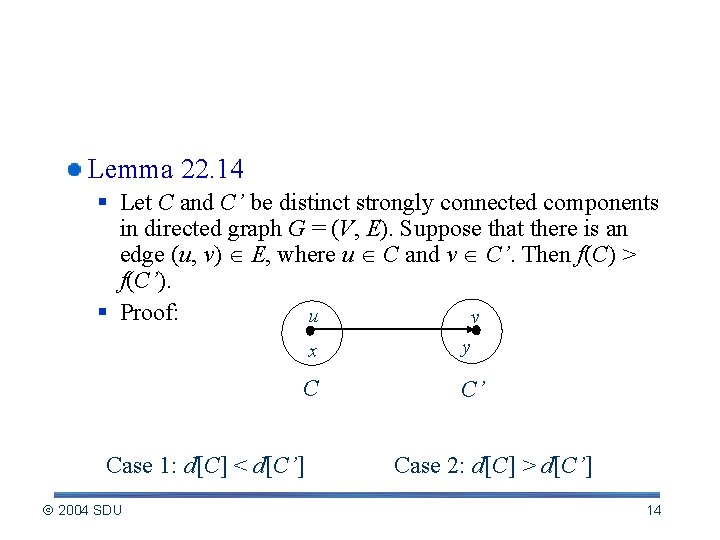
A Key Property Related to SCCs and finishing times Lemma 22. 14 § Let C and C’ be distinct strongly connected components in directed graph G = (V, E). Suppose that there is an edge (u, v) E, where u C and v C’. Then f(C) > f(C’). § Proof: u v x y C C’ Case 1: d[C] < d[C’] 2004 SDU Case 2: d[C] > d[C’] 14

Can we order the f[u] for all vertices and search from the smallest f[u]? C 1 C 2 C 3 C 4 C 5 f(C 1)>f(C 2)>f(C 3)… 2004 SDU 15

A Corollary 22. 15 § Let C and C’ be distinct strongly connected components in directed graph G = (V, E). Suppose that there is an edge (u, v) ET, where u C and v C’. Then f(C) < f(C’). § Here, the finishing time is got from the first depth-search § Proof: – (u, v) ET (v, u) E, G and G’ have the same strongly connected components, Lemma 22. 14 implies f(C) < f(C’). 2004 SDU 16

Can we search from the largest f[u] in GT? C 1 C 2 C 3 C 4 C 5 f(C 1)>f(C 2)>f(C 3)… 2004 SDU 17

Correctness of the Algorithm Theorem 22. 16 § § STRONGLY-CONNECTED-COMPONENTS(G) correctly computes the strongly connected components of a directed graph G. Proof: By induction on the number k of depth-first trees found in line 3, prove that the vertices of each tree form a strongly connected component, that is 1. The vertex set V(T) of each depth-first tree contains all the vertices of a strongly connected component C 2. V(T) dose not contain any more vertices other than those of C – Basic step: k = 0, it is trivially true. 2004 SDU 18

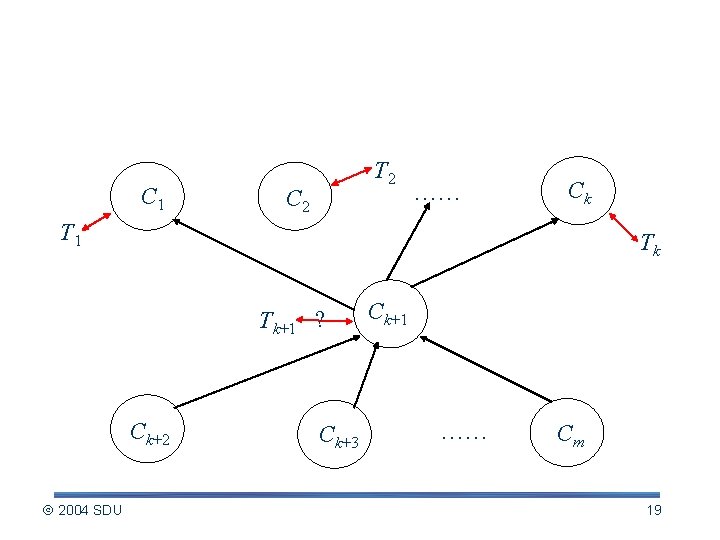
Proof (Continued) C 1 T 2 C 2 …… Ck T 1 Tk Tk+1 ? Ck+2 2004 SDU Ck+3 Ck+1 …… Cm 19

Proof (continued) Inductive step: Assume that each of the first k depth-first trees produced in line 3 is a strongly connected component. Consider the (k+1)st tree produced. § Let the root of the tree be vertex u, and let u be in strongly connected component C. By induction hypothesis, no vertices in C had been searched before, and since u has the biggest f[] among all the remaining vertices, f[u] = f[C] > f[C’] for any strongly connected component C’ other than C that has yet not been visited. 2004 SDU 20

Proof (continued ) 1. At time d[u], all other vertices of C are white. By the white-path theorem, all other vertices of C are descendants of u in its depth-first tree. 2. Moreover, by induction hypothesis and Corollary 22. 15, any edge in GT that leaves C must point to SCC that have already been visited. Thus, no vertex in any SCC other than C will be a descendant of u during the depthfirst search of GT. Thus, the vertices of the depth-first tree in GT that is rooted at u form exactly one strongly connected component. 2004 SDU 21

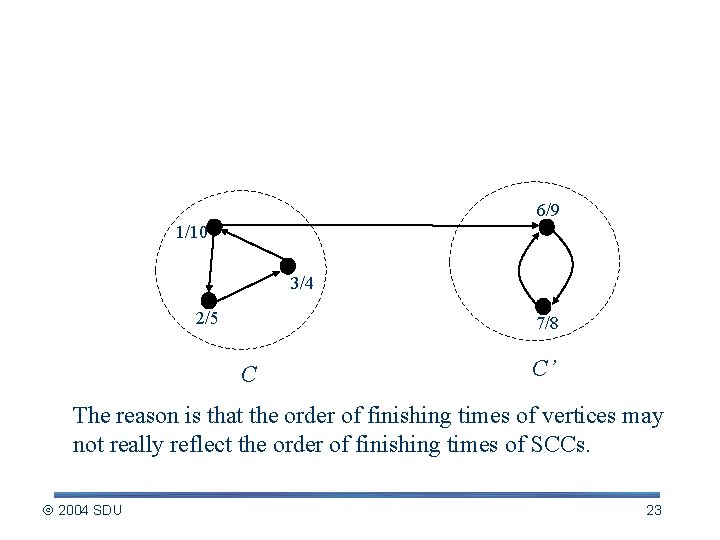
A Conjecture Prof Deaver: The algorithm for strongly connected components can be simplified by using the original (instead of the transpose) graph in the second depthfirst search and scanning the vertices in order of increasing finishing times. Is the conjecture correct? 2004 SDU 22

The Answer 6/9 1/10 3/4 2/5 7/8 C C’ The reason is that the order of finishing times of vertices may not really reflect the order of finishing times of SCCs. 2004 SDU 23

Semi-connected Graph A directed graph G = (V, E) is semi-connected if for all pairs of vertices u, v V, we have u v (v is reachable from u) or v u (u is reachable from v) or both. How to determine whether or not a directed graph is semi-connected? (Exercise 22. 5 -7) 2004 SDU 24

An Observation Given a directed graph G = (V, E), its strongly connected component graph is denoted as GSSC = (VSCC, ESCC). Then G is semi-connected if and only if for any pair of vertices u, v VSSC, either u is reachable from v or v is reachable from u ( notice that there can not be paths in both directions). 2004 SDU 25

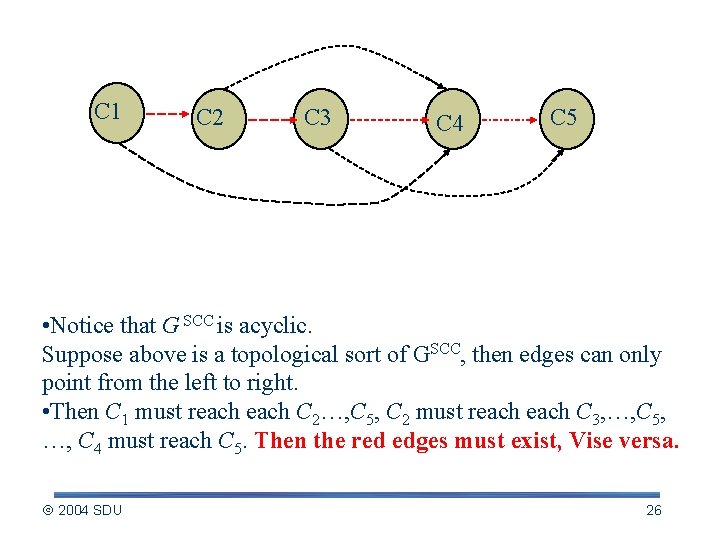
C 1 C 2 C 3 C 4 C 5 • Notice that G SCC is acyclic. Suppose above is a topological sort of GSCC, then edges can only point from the left to right. • Then C 1 must reach C 2…, C 5, C 2 must reach C 3, …, C 5, …, C 4 must reach C 5. Then the red edges must exist, Vise versa. 2004 SDU 26

The Algorithm Outline 1. 2. 3. 4. Compute the strongly connected components of G. Construct the component graph GSCC of G. Topological Sort GSCC. Judge whethere is an edge from Ci to Ci+1, for 0<i<m, if no, return “no”, where Ci is indexed by topological sort, and m is the number of SCCs. 5. Return “yes”. Ø Time complexity: (V + E) 2004 SDU 27

Another method In step 3, generate topological sort by using the method that each time finding a vertex of zero indegree. Then G is semi-connected if and only if in each run, exactly one vertex of in-degree zero exists. Proof? simple by induction on # of SCCs. 2004 SDU 28

An Example (a): The graph G with its SCCs shaded (b): The transpose GT of G with SCCs shaded (c): The component graph GSCC = (VSCC, ESCC) of G 2004 SDU 29

Remarks Until now, we have introduced § § Directed graph Singly connected graph Semi-connected graph Strongly connected graph 2004 SDU 30

Exercises Page 175: 22. 4 -3 Page 172: 22. 3 -12 Page 180: 22. 5 -5(22. 1 -4) 2004 SDU 31

2004 SDU 32