MultiWay search Trees 1 2 3 Trees a

Multi-Way search Trees 1. 2 -3 Trees: a. Nodes may contain 1 or 2 items. b. A node with k items has k + 1 children c. All leaves are on same level.

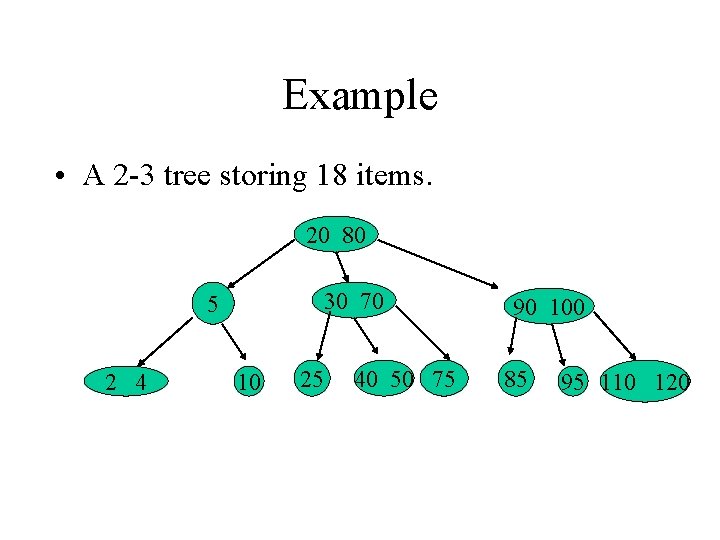
Example • A 2 -3 tree storing 18 items. 20 80 30 70 5 2 4 10 25 40 50 75 90 100 85 95 110 120

Updating • Insertion: • Find the appropriate leaf. If there is only one item, just add to leaf. • Insert(23); Insert(15) • If no room, move middle item to parent and split remaining two item among two children. • Insert(3);

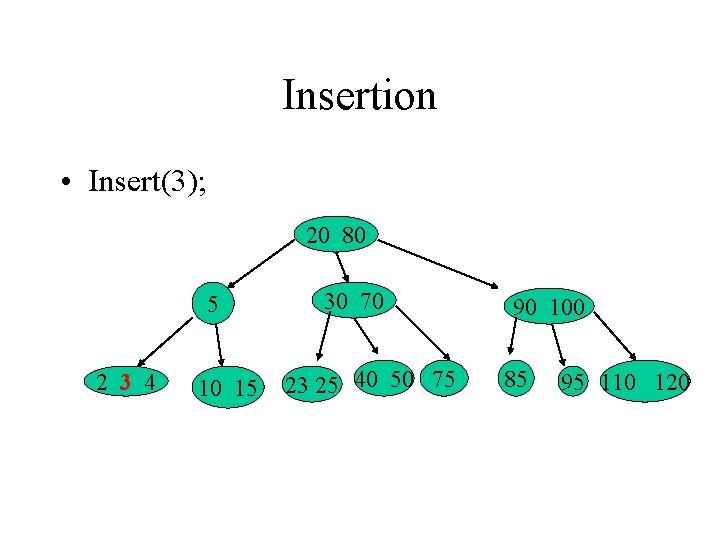
Insertion • Insert(3); 20 80 5 2 3 4 10 15 30 70 23 25 40 50 75 90 100 85 95 110 120

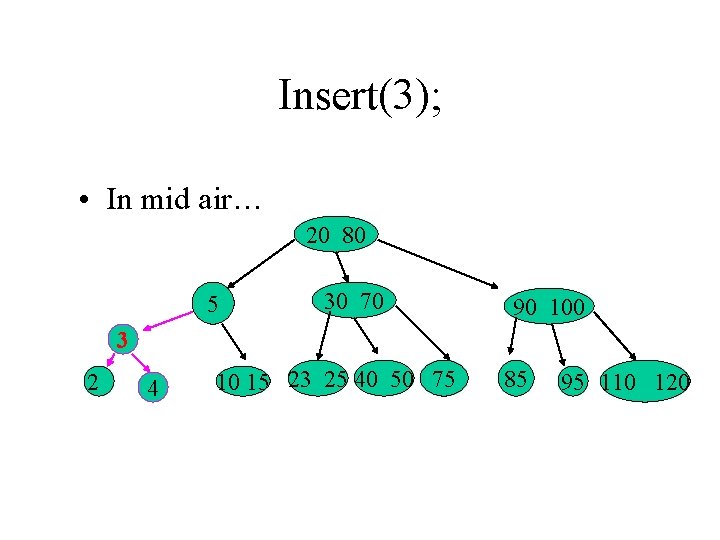
Insert(3); • In mid air… 20 80 5 30 70 90 100 3 2 4 10 15 23 25 40 50 75 85 95 110 120

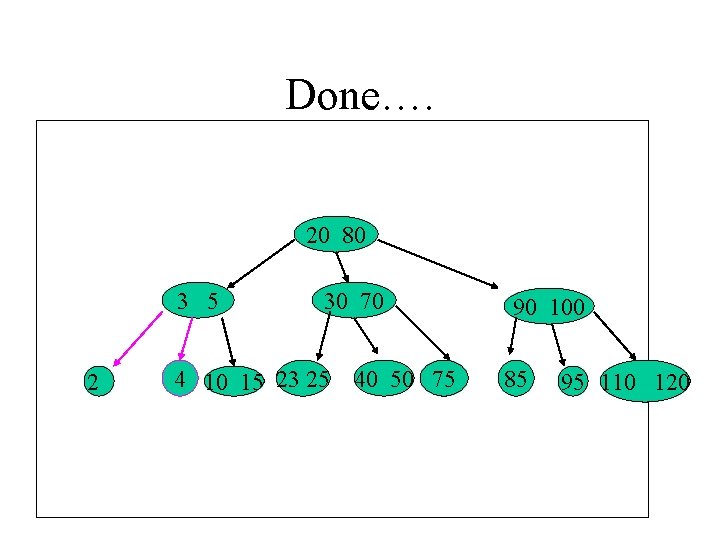
Done…. 20 80 3 5 2 30 70 4 10 15 23 25 40 50 75 90 100 85 95 110 120

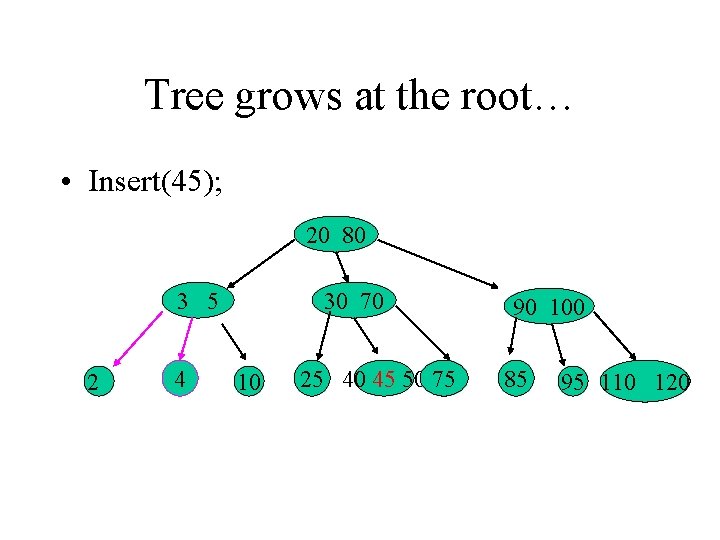
Tree grows at the root… • Insert(45); 20 80 3 5 2 4 30 70 10 25 40 45 50 75 90 100 85 95 110 120

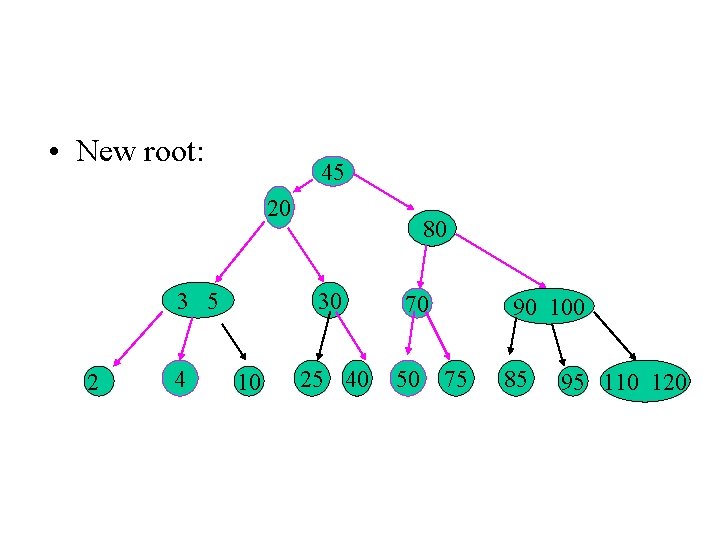
• New root: 45 20 3 5 2 4 80 30 10 25 40 70 50 90 100 75 85 95 110 120

Delete • If item is not in a leaf exchange with inorder successor. • If leaf has another item, remove item. • Examples: Remove(110); • (Insert(110); Remove(100); ) • If leaf has only one item but sibling has two items: redistribute items. Remove(80);

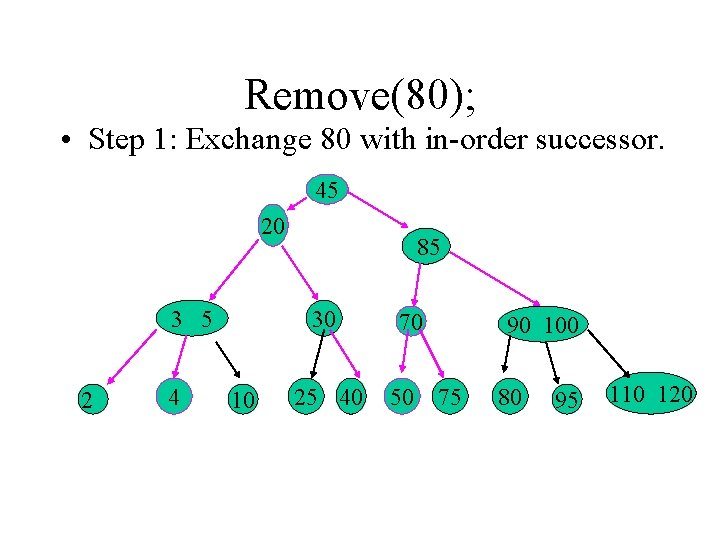
Remove(80); • Step 1: Exchange 80 with in-order successor. 45 20 3 5 2 4 85 30 10 25 40 70 50 90 100 75 80 95 110 120

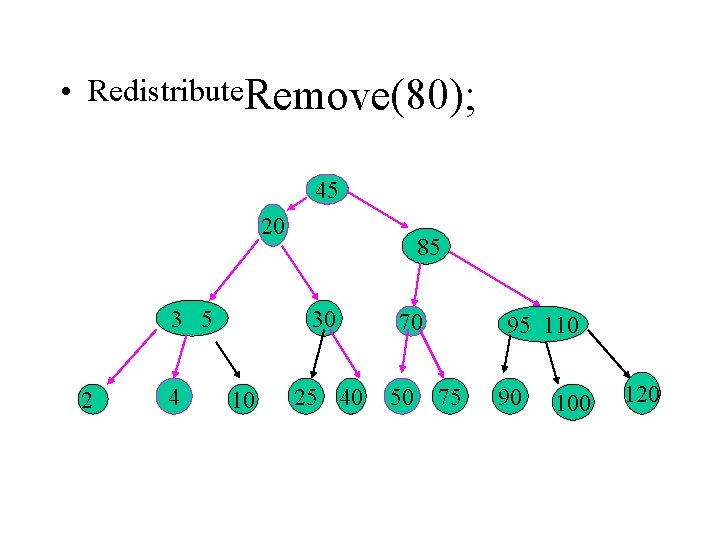
• Redistribute. Remove(80); 45 20 3 5 2 4 85 30 10 25 40 70 50 95 110 75 90 100 120

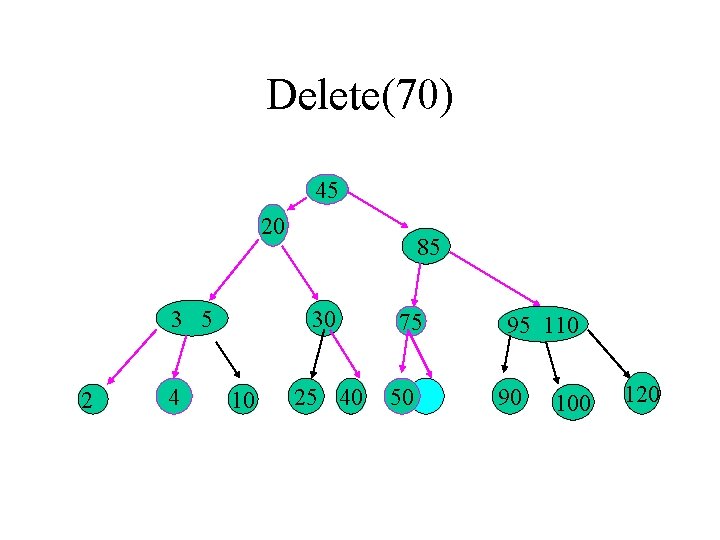
Some more removals… • Remove(70); Swap(70, 75); Remove(70); “Merge” Empty node with sibling; Join parent with node; Now every node has k+1 children except that one node has 0 items and one child. Sibling 1 110 can spare an item: redistribute.

Delete(70) 45 20 3 5 2 4 85 30 10 25 40 75 50 95 110 90 100 120

New tree: • Delete(75) will “shrink” the tree. 45 20 3 5 2 4 95 30 10 75 25 40 50 110 90 100 120

Details • • • 1. Swap(75, 90) //inorder successor 2. Remove(75) //empty node created 3. Merge with sibling 4. Drop item from parent// (50, 90) empty Parent 5. Merge empty node with sibling, drop item from parent (95) • 6. Parent empty, merge with sibling drop item. Parent (root) empty, remove root.

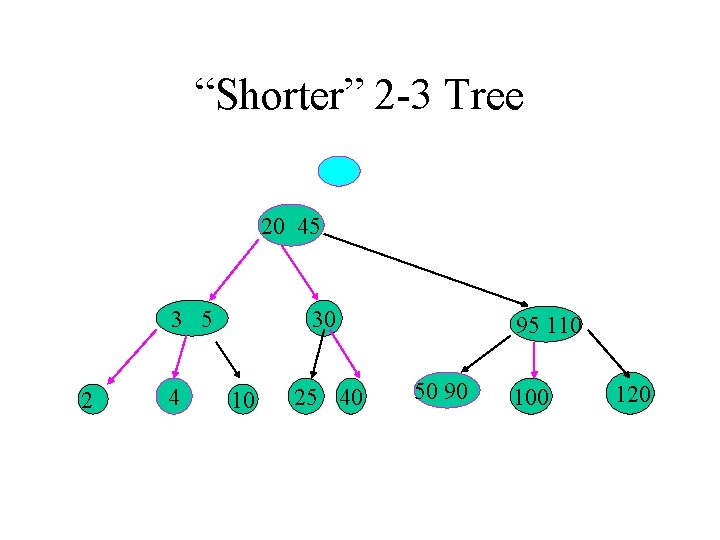
“Shorter” 2 -3 Tree 20 45 3 5 2 4 30 10 25 40 95 110 50 90 100 120

Deletion Summary • If item k is present but not in a leaf, swap with inorder successor; • Delete item k from leaf L. • If L has no items: Fix(L); • Fix(Node N); • //All nodes have k items and k+1 children • // A node with 0 items and 1 child is possible, it will have to be fixed.

Deletion (continued) • If N is the root, delete it and return its child as the new root. • Example: Delete(8); 5 5 1 3 2 8 3 3 Return 35 35

Deletion (Continued) • If a sibling S of N has 2 items distribute items among N, S and the parent P; if N is internal, move the appropriate child from S to N. • Else bring an item from P into S; • If N is internal, make its (single) child the child of S; remove N. • If P has no items Fix(P) (recursive call)

(2, 4) Trees • Size Property: nodes may have 1, 2, 3 items. • Every node, except leaves has size+1 children. • Depth property: all leaves have the same depth. • Insertion: If during the search for the leaf you encounter a “full” node, split it.

(2, 4) Tree 10 3 8 45 25 60 50 55 70 90 100

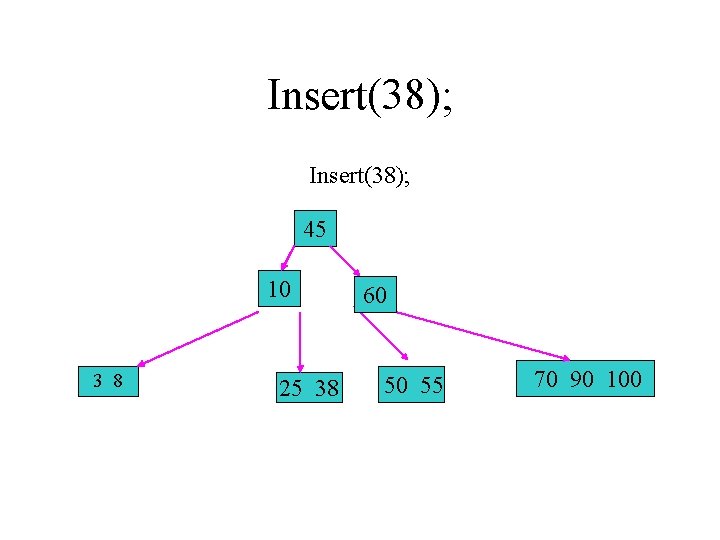
Insert(38); 45 10 3 8 25 38 60 50 55 70 90 100

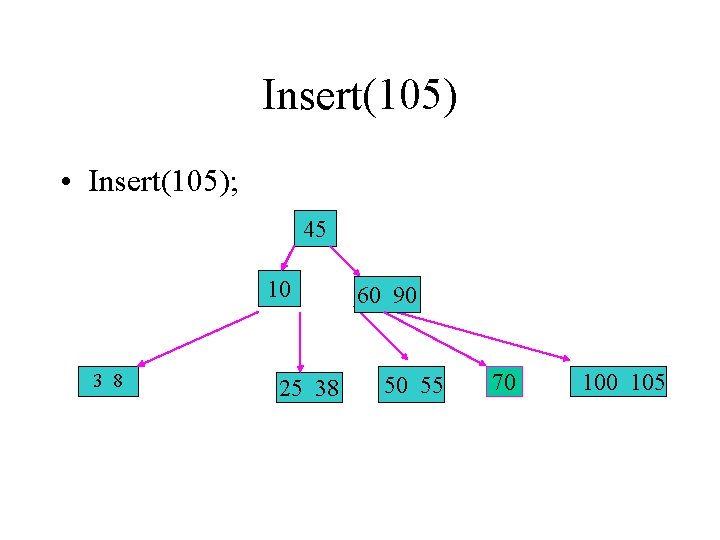
Insert(105) • Insert(105); 45 10 3 8 25 38 60 90 50 55 70 105

Removal • As with BS trees, we may place the node to be removed in a leaf. • If the leaf v has another item, done. • If not, we have an UNDERFLOW. • If a sibling of v has 2 or 3 items, transfer an item. • If v has 2 or 3 siblings we perform a transfer

Removal • If v has only one sibling with a single item we drop an item from the parent to the sibling, remove v. This may create an underflow at the parent. We “percolate” up the underflow. It may reach the root in which case the root will be discarded and the tree will “shrink”.

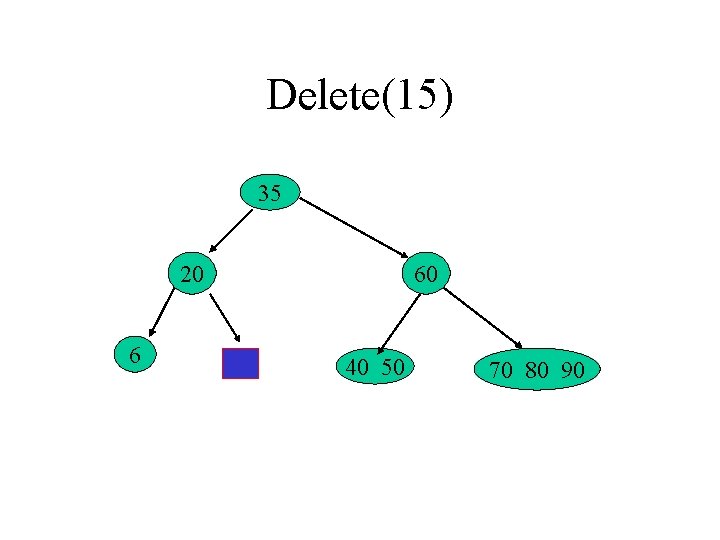
Delete(15) 35 20 6 60 15 40 50 70 80 90

Delete(15) 35 20 6 60 40 50 70 80 90

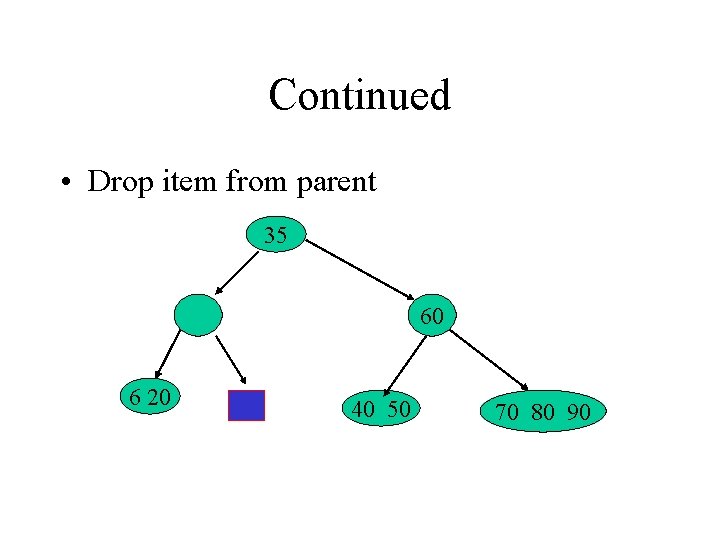
Continued • Drop item from parent 35 60 6 20 40 50 70 80 90

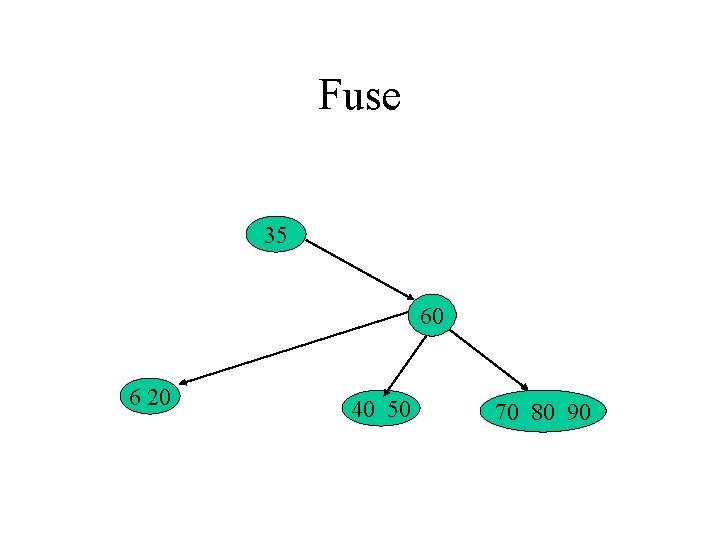
Fuse 35 60 6 20 40 50 70 80 90

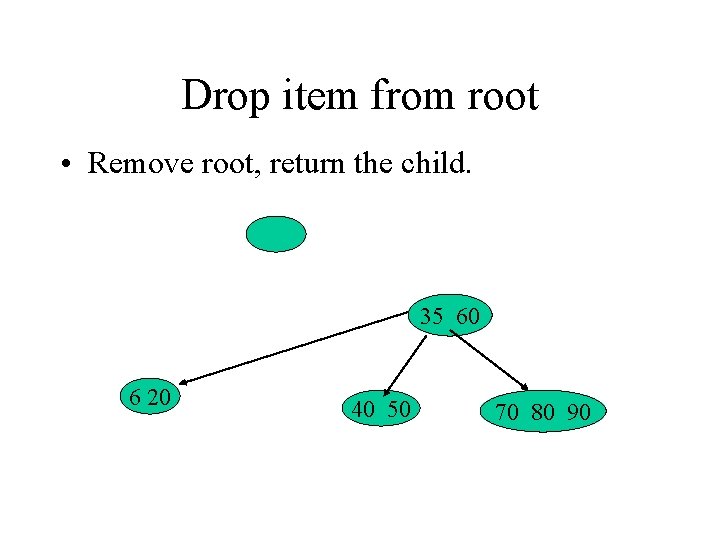
Drop item from root • Remove root, return the child. 35 60 6 20 40 50 70 80 90

Summary • Both 2 -3 tress and 2 -4 trees make it very easy to maintain balance. • Insertion and deletion easier for 2 -4 tree. • Cost is waste of space in each node. Also extra comparison inside each node. • Does not “extend” binary trees.

Red-Black Trees • Root property: Root is BLACK. • External Property: Every external node is BLACK • Internal property: Children of a RED node are BLACK. • Depth property: All external nodes have the same BLACK depth.

Red. Black Insertion

Red Black Trees, Insertion 1. Find proper external node. 2. Insert and color node red. 3. No black depth violation but may violate the red-black parent-child relationship. 4. Let: z be the inserted node, v its parent and u its grandparent. If v is red then u must be black.

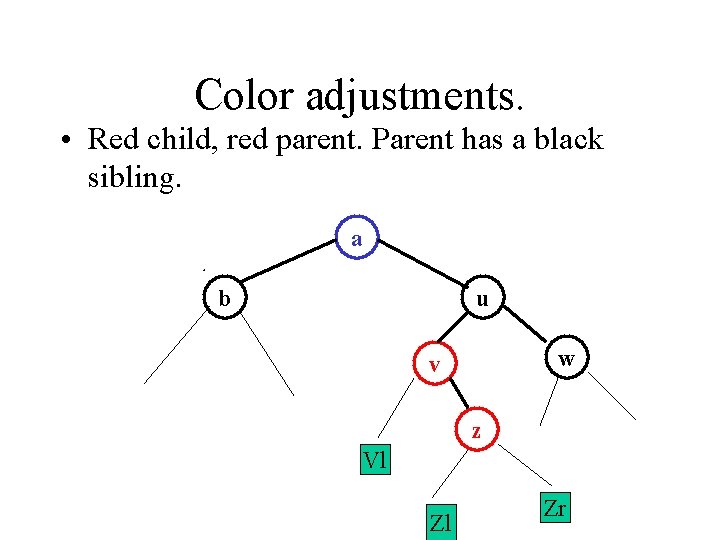
Color adjustments. • Red child, red parent. Parent has a black sibling. a b u w v z Vl Zl Zr

Rotation • Z-middle key. Black height does not change! No more red-red. a b z u v Vl Zl Zr w

Color adjustment II a b u w v Vr z Zl Zr

Rotation II a b v u z Zl Zr Vr w

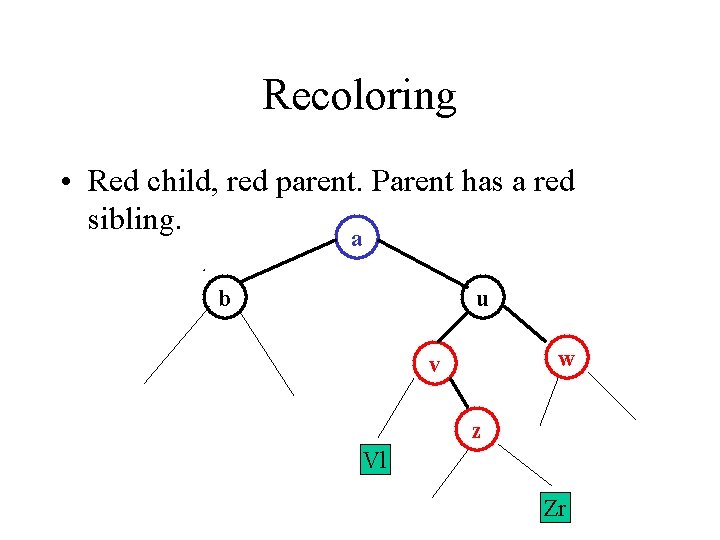
Recoloring • Red child, red parent. Parent has a red sibling. a b u w v z Vl Zr

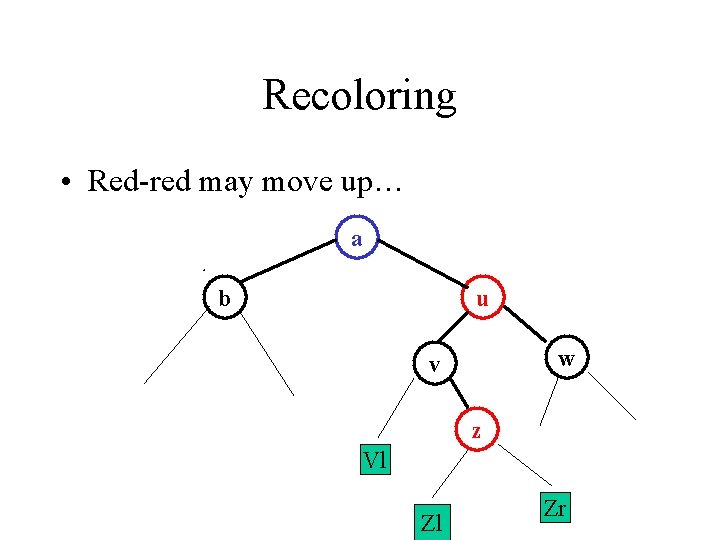
Recoloring • Red-red may move up… a b u w v z Vl Zl Zr

Red Black Tree • Insert 10 – root 10

Red Black Tree • Insert 10 – root 10

Red Black Tree • Insert 85 10 85

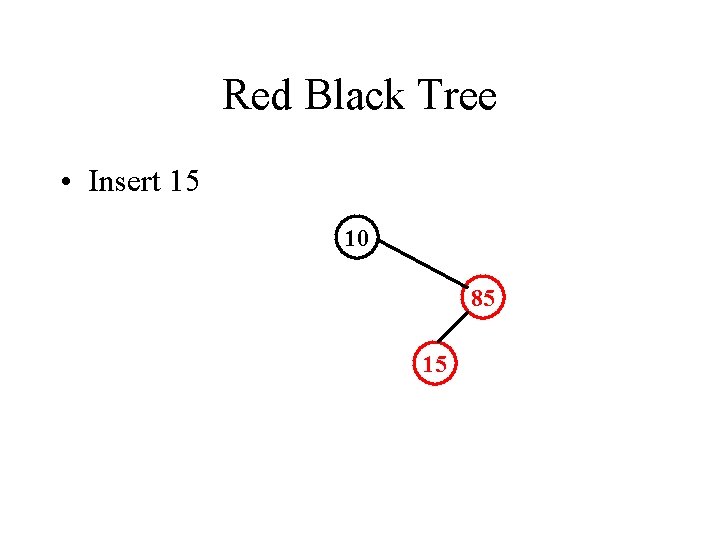
Red Black Tree • Insert 15 10 85 15

Red Black Tree • Rotate – Change colors 15 10 85

Red Black Tree • Insert 70 15 10 85 70

Red Black Tree • Change Color 15 10 85 70

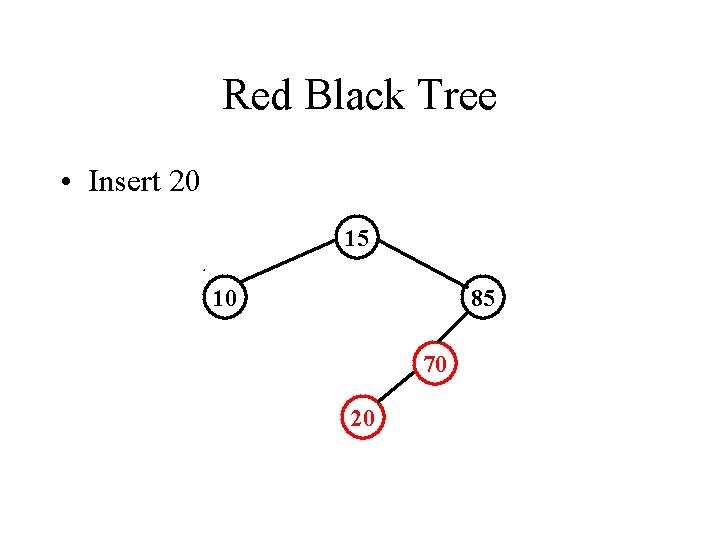
Red Black Tree • Insert 20 15 10 85 70 20

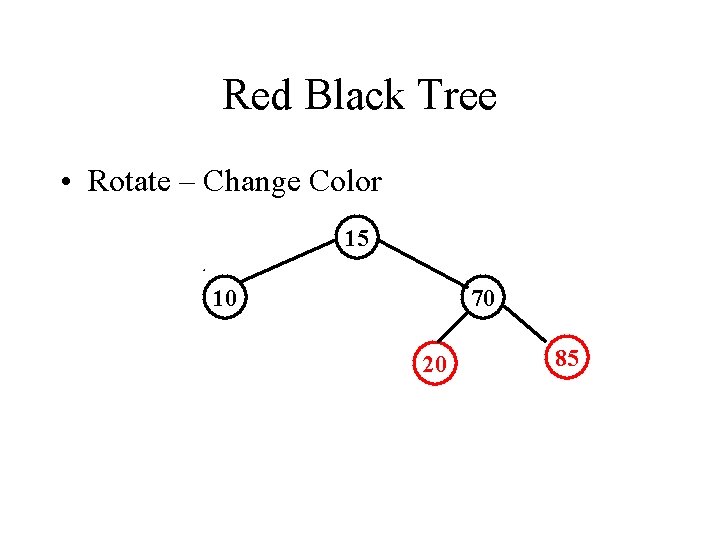
Red Black Tree • Rotate – Change Color 15 10 70 20 85

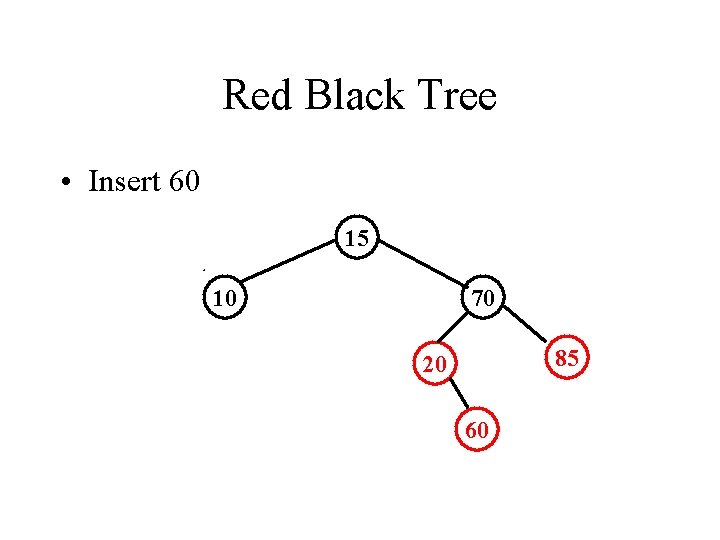
Red Black Tree • Insert 60 15 10 70 85 20 60

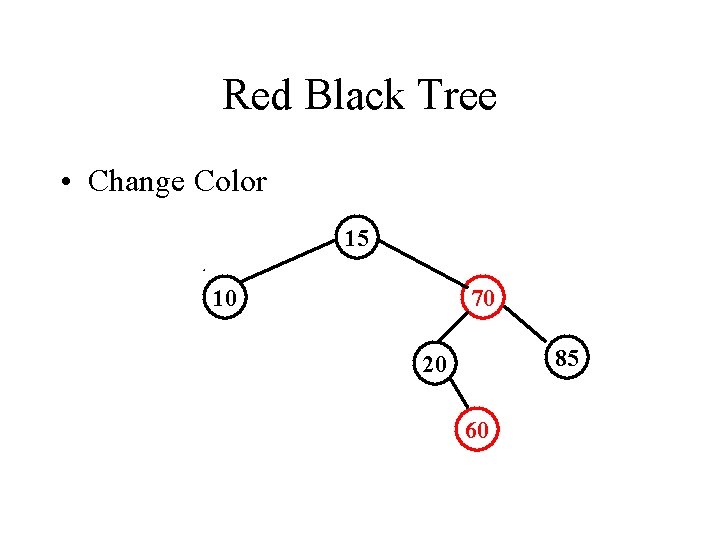
Red Black Tree • Change Color 15 10 70 85 20 60

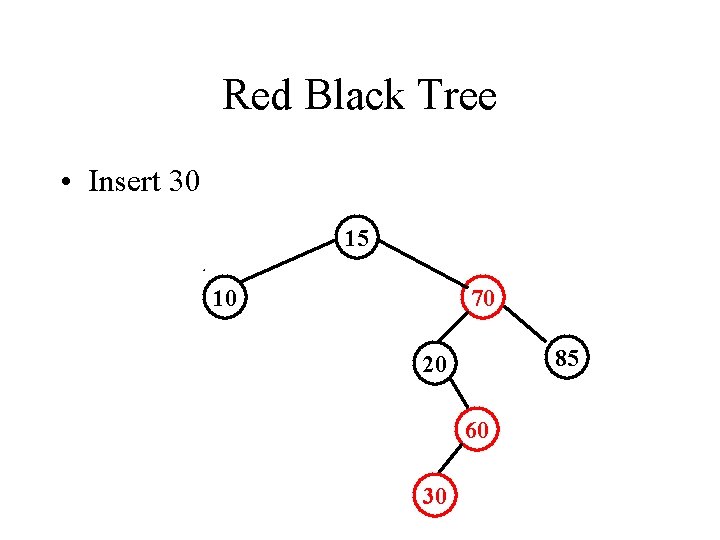
Red Black Tree • Insert 30 15 10 70 85 20 60 30

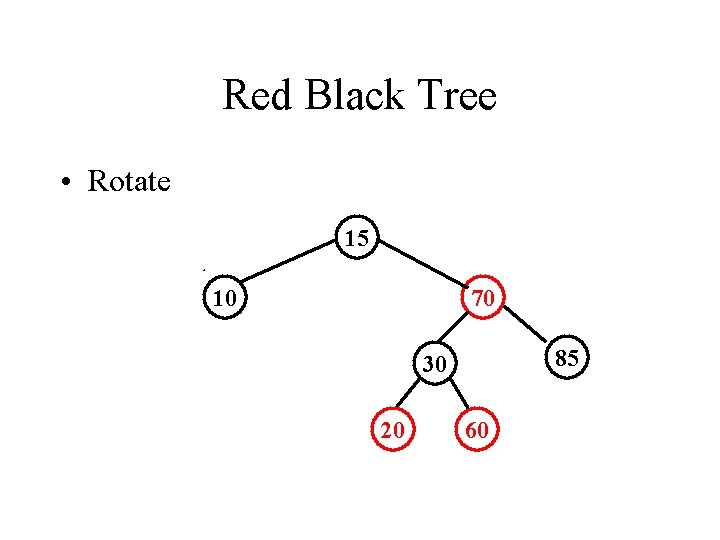
Red Black Tree • Rotate 15 10 70 85 30 20 60

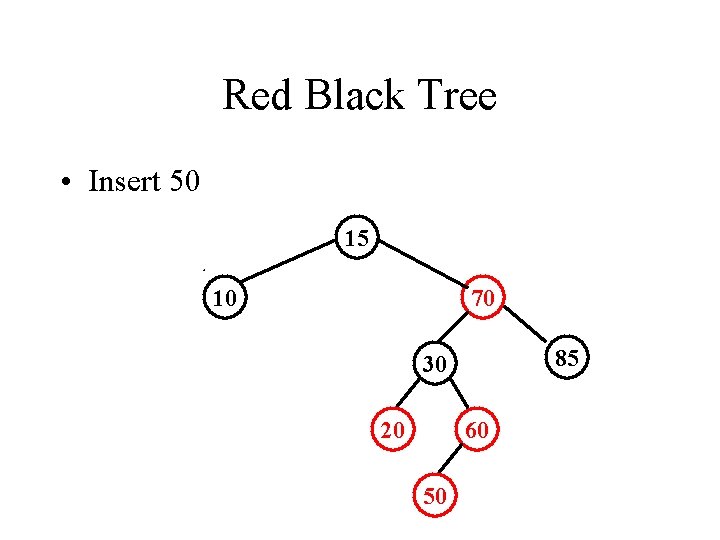
Red Black Tree • Insert 50 15 10 70 85 30 20 60 50

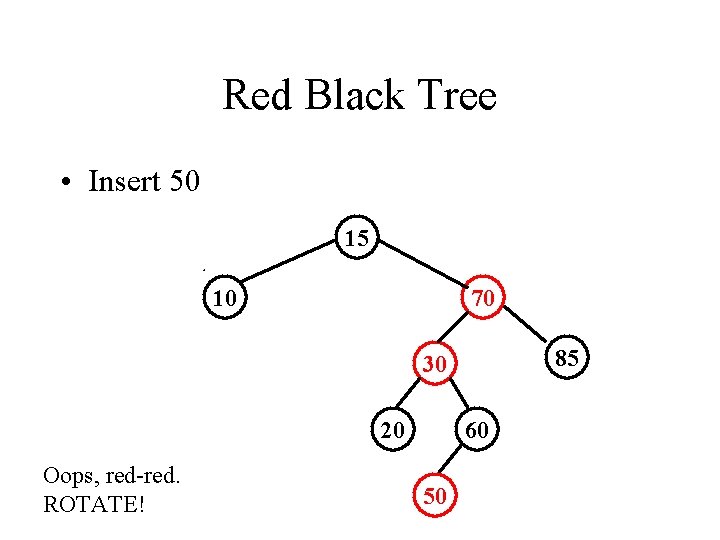
Red Black Tree • Insert 50 15 10 70 85 30 20 Oops, red-red. ROTATE! 60 50

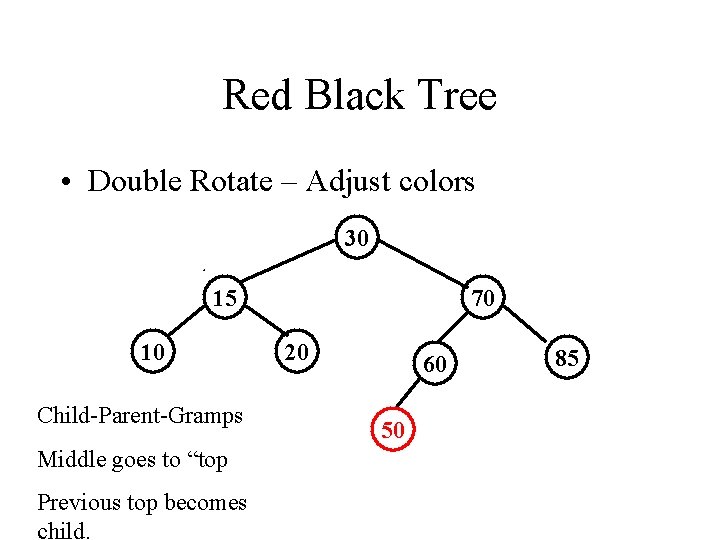
Red Black Tree • Double Rotate – Adjust colors 30 15 10 Child-Parent-Gramps Middle goes to “top Previous top becomes child. 70 20 60 50 85

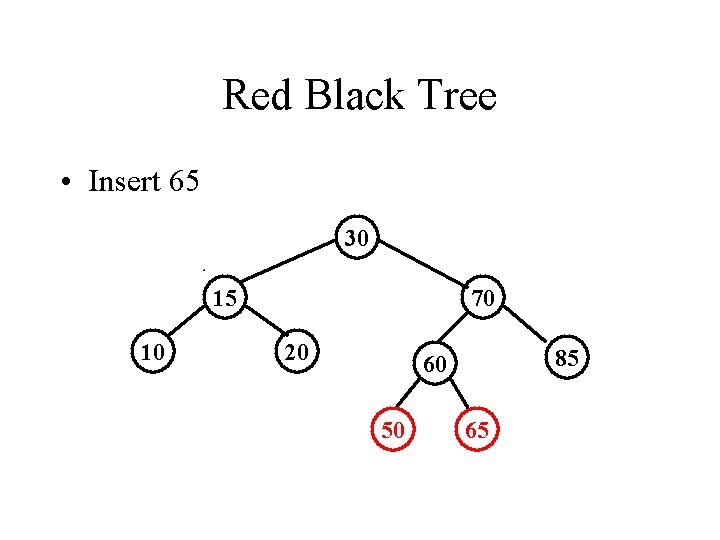
Red Black Tree • Insert 65 30 15 10 70 20 85 60 50 65

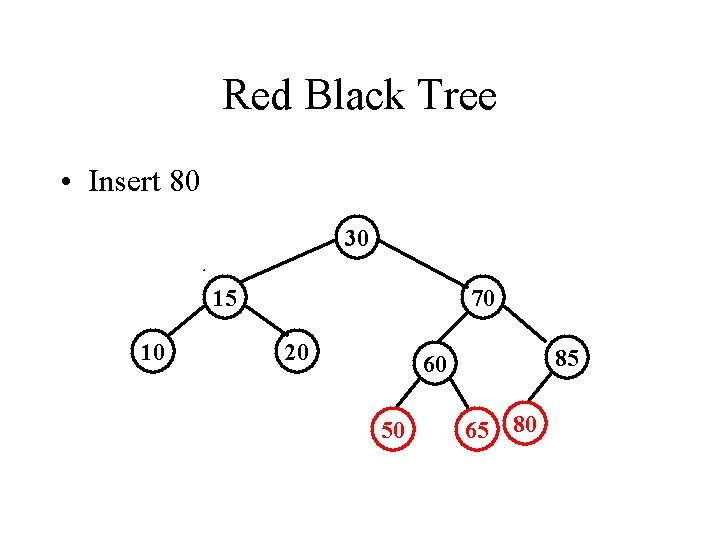
Red Black Tree • Insert 80 30 15 10 70 20 85 60 50 65 80

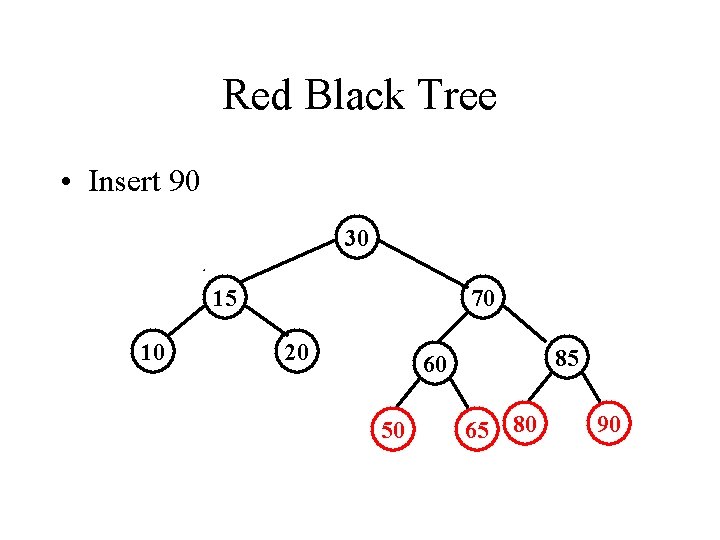
Red Black Tree • Insert 90 30 15 10 70 20 85 60 50 65 80 90

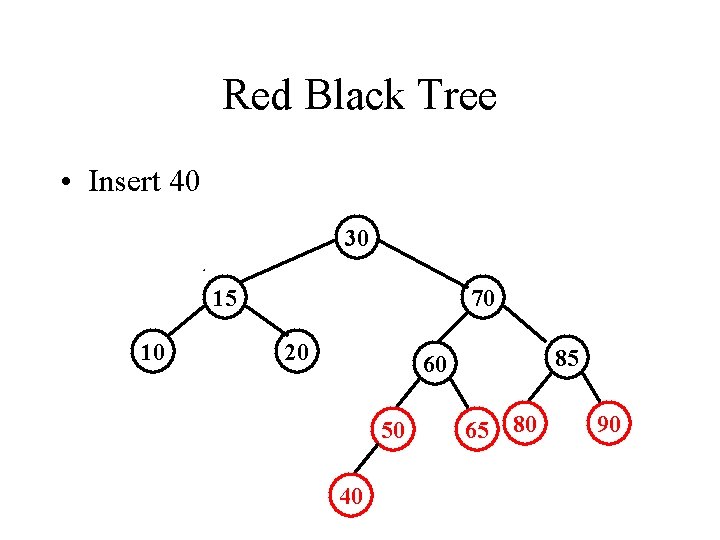
Red Black Tree • Insert 40 30 15 10 70 20 85 60 50 40 65 80 90

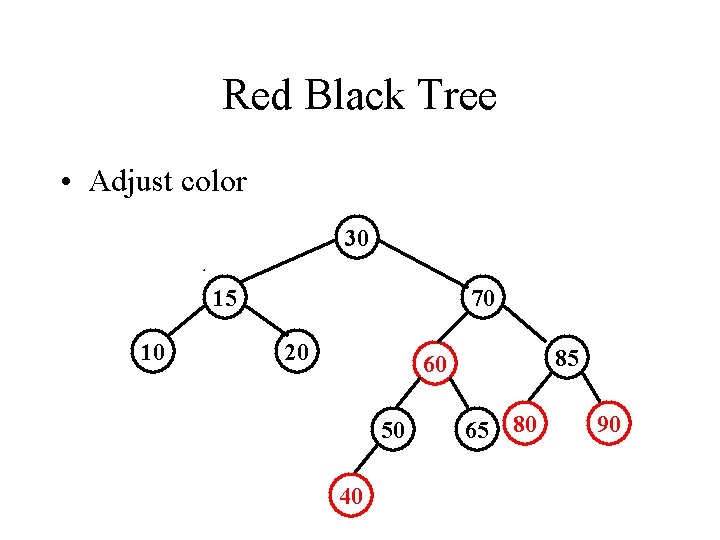
Red Black Tree • Adjust color 30 15 10 70 20 85 60 50 40 65 80 90

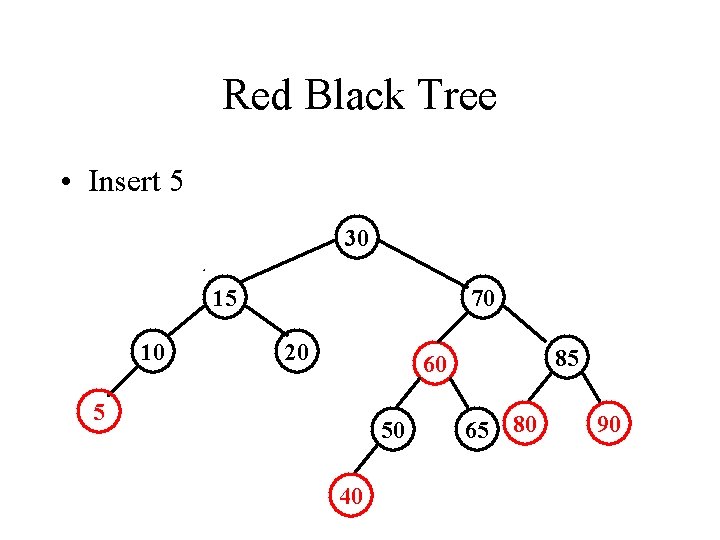
Red Black Tree • Insert 5 30 15 10 70 20 85 60 5 50 40 65 80 90

Red Black Tree • Insert 55 30 15 10 70 20 85 60 5 50 40 65 55 80 90