Binary Trees and Binary Search Trees Binary Trees

Binary Trees and Binary Search Trees

Binary Trees • A binary tree is a tree. • Each node has one or two children. • Examples are – Arithmetic expression (7 -8)* (3+9) – Logical expressions (T and T) or (F and not T)

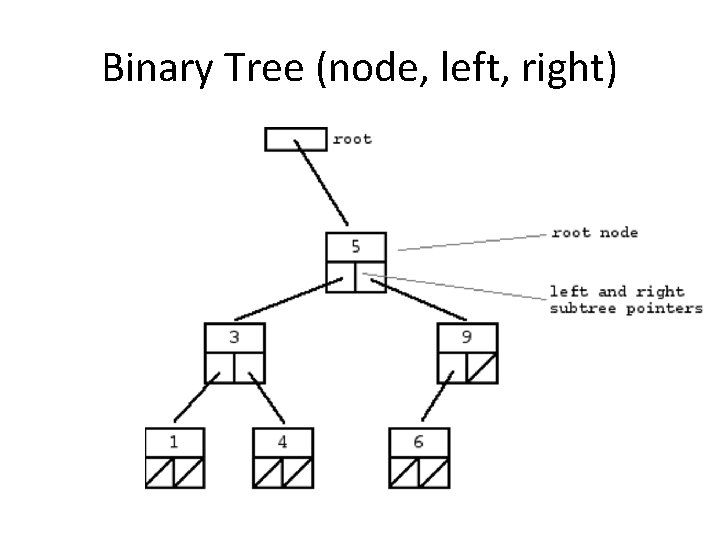
Binary Tree (node, left, right)

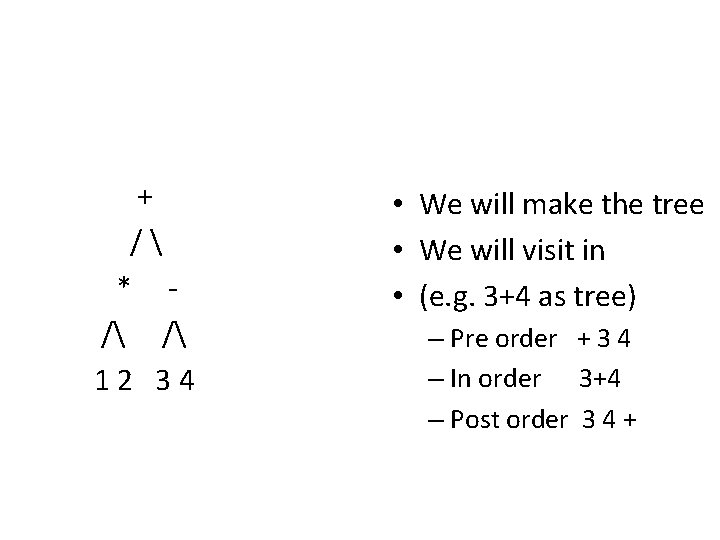
+ / * / / 12 34 • We will make the tree • We will visit in • (e. g. 3+4 as tree) – Pre order + 3 4 – In order 3+4 – Post order 3 4 +

A node class • We will have a node class (for binary trees) • It will store some data • It will have all the associated get/set methods

data attributes private String data; // the data we are storing at the node private Node left; // object reference to node at left. private Node right; // object reference to node at right.

methods public Node(String data) { // constructor public String get. Node() { // getter methods public void set. Node(String data) { // setter method public Node get. Left() { // get the left child public void set. Left(Node left) { // set the left child public Node get. Right() { // get the right child public void set. Right(Node right) { // set the right child public boolean has. Left() { // does the node have a left child public boolean has. Right() { // does the node have a right child public String to. String() { // returns String containing data in node.

to. String • The purpose of a to. String method is to represent the object as a string • E. g. in a person class with name and age • public String to. String() { • return “name ”+name+” age ”+ age • } • //this will give the “class attributes” as a single string

constructor • public Tree. Binary. Node(T data) { • this. data = data; • }

Get/set node public String get. Node() { // getter methods return this. data; } public void set. Node(String data) { // setter method this. data = data; }

Get/set left • public Node get. Left() { • return this. left; • } • public void set. Left(Node left) { • this. left = left; • }

Get/set right • public Node get. Right() { • return this. right; • } • public void set. Right(Node right) { • this. right = right; • }

Has left/right • public boolean has. Left() { • return left != null; • } • public boolean has. Right() { • return right != null; • }

to. String() • //returns a String containing the data in the node. • public String to. String() { • return this. get. Node(). to. String(); • }

preorder • • When displaying, 1/ display node first 2/ then the left tree 3/ then the right tree • E. g. + 2 3

Pre-order • public static void preorder(Node node) { • if (node != null) { • System. out. print(node. get. Node() + " "); • preorder(node. get. Left()); • preorder(node. get. Right()); • }

In order • • When displaying, 1/ then the left tree 2/ display node first 3/ then the right tree • E. g. 2 + 3

In-order • public static void inorder(Node node) { • if (node != null) { • inorder(node. get. Left()); • System. out. print(node. get. Node() + " "); • inorder(node. get. Right()); • }

Post order • • When displaying, 1/ then the left tree 2/ then the right tree 3/ display node first • E. g. 2 3 +

Post-order • public static void postorder(Node node) { • if (node != null) { • postorder(node. get. Left()); • postorder(node. get. Right()); • System. out. print(node. get. Node() + " "); • }

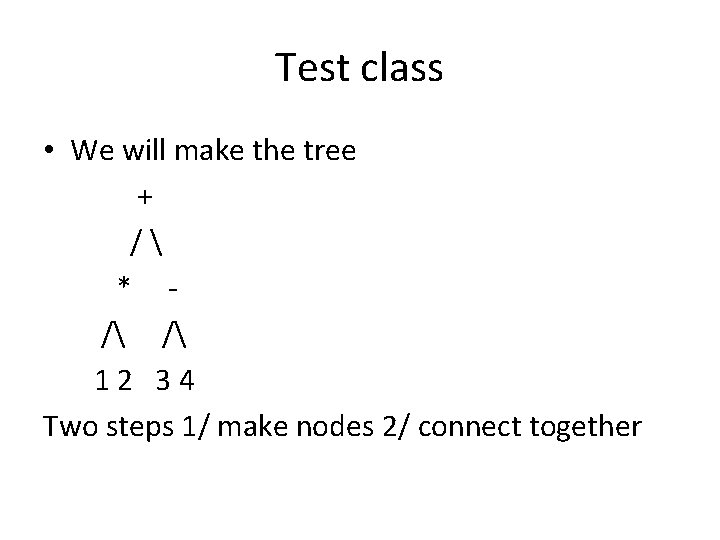
Test class • We will make the tree + / * / / 12 34 Two steps 1/ make nodes 2/ connect together

make nodes • // set up some numbers - as STRINGS • Tree. Binary. Node<String> one = new Tree. Binary. Node<String>("1"); • Tree. Binary. Node<String> two = new Tree. Binary. Node<String>("2"); • Tree. Binary. Node<String> three = new Tree. Binary. Node<String>("3"); • Tree. Binary. Node<String> four = new Tree. Binary. Node<String>("4");

make some more nodes // set up some arithmetic operators - as STRINGS • Tree. Binary. Node<String> add = new Tree. Binary. Node<String>("+"); • Tree. Binary. Node<String> mul = new Tree. Binary. Node<String>("*"); • Tree. Binary. Node<String> sub = new Tree. Binary. Node<String>("-");

Connect together We use setleft/right to connect add. set. Left(mul); add. set. Right(sub); mul. set. Left(one); mul. set. Right(two); sub. set. Left(three); sub. set. Right(four);

printing • • • We will now display the trees Pre order In order Post order Level order

Mul pre/in/post order • • *12 1*2 12* *12

Add pre/in/post order • • +*12 -34 1*2+3 -4 12*34 -+ +*-1234

Sub pre/in/post order • • -34 3 -4 34 -34

Summary • A binary tree has nodes with 0 1 or 2 children. • We can print in at least 3 ways – there are more. • Use to model arithmetic and logic expressions. • where a hierarchy exists • We will now look at binary search trees.

Concept of Binary Search Tree

Compare. To method • • A compare to method public int compare. To(Node node) Returns int Negative if before in ordering Zero – if equal order Positive if after in ordering Therefore using this we can order a set of item.

Additional method in Node class • //THIS IS A NEW METHOD • public int compare. To(Node node) { • return this. data. to. String(). compare. To(nod e. get. Node(). to. String()); • }

attributes private Node root; // The root Node of the tree private int size = 0; // A count of the Nodes in the tree

Size/clear/is. Empty // Returns the number of Nodes in the tree. public int size() { return size; } // Empties the tree public void clear() { this. root = null; size = 0; } // Determines if the tree is empty or not. public boolean is. Empty() { return (root == null); }

add a node public void add. Node(Node node. To. Insert) { // If tree is empty, make our new Node the root if (root == null) { root = node. To. Insert; size = 1; } else { // recursive calls to add the descendants of Node add. Node(node. To. Insert, root); // PRIVATE METHOD size = size + 1; } }

private void add. Node(Node // private adds a node private void add. Node(Node node. To. Insert, Node current. Node) { if (node. To. Insert. compare. To(current. Node) < 0) { if (current. Node. has. Left()) add. Node(node. To. Insert, current. Node. get. Left()); else { current. Node. set. Left(node. To. Insert); return; } } else { if (current. Node. has. Right()) add. Node(node. To. Insert, current. Node. get. Right()); else { current. Node. set. Right(node. To. Insert); return; }}}

// pre. Order public String pre. Order() { String. Buffer string. Buffer = new String. Buffer(); if (root == null) return "Empty Tree!"; else pre. Order(root, string. Buffer); return string. Buffer. to. String(); }

// private pre. Order private void pre. Order(Node, String. Buffer string. Buffer) { //visit the Nodes and add contents to our String string. Buffer. append(node. get. Node(). to. String() + ", "); // 1 Visit Node if (node. has. Left()) pre. Order(node. get. Left(), string. Buffer); // 2 Visit left if (node. has. Right()) pre. Order(node. get. Right(), string. Buffer); // 3 Visit right }

find public String find(String name) { return find(name, root); } //find(name, root) is a private method – and looks for name from the current node.

3 choices The node we are looking for is either 1/ at the current node in the tree we are looking at • OR It is to the left OR it is to the right. • We can decide which branch to go down using compare. To

private String find(String name, Node node) { if (node == null) return null; int order = name. compare. To(node. get. Node(). to. String()); if (order == 0) return node. get. Node(); if (node. has. Left() && order < 0) return find(name, node. get. Left()); if (node. has. Right() && order > 0) return find(name, node. get. Right()); return null; }

Example • We will Make some nodes (containing letters) Add the nodes to the tree. Print out the tree as we add the node to see where it adds them (i. e. does it maintain order)

make a tree to store some Nodes Tree. Search. Binary letters = new Tree. Search. Binary(); // make some Node a = new Node b = new Node c = new Node x = new Node y = new Node z = new nodes Node("a"); Node("b"); Node("c"); Node("x"); Node("y"); Node("z");

connect nodes and print trees • • letters. add. Node(b); letters. add. Node(c); letters. add. Node(a); letters. add. Node(z); letters. add. Node(x); letters. add. Node(y); //try this now

• // connect nodes and print the trees • letters. add. Node(b); • letters. print. Tree(); • b

• letters. add. Node(c); • letters. print. Tree(); • c • b

• letters. add. Node(a); • letters. print. Tree(); • c • b • a

• letters. add. Node(z); • letters. print. Tree(); • z • c • b • a

• letters. add. Node(x); • letters. print. Tree(); • z • • c • b • a x

• letters. add. Node(y); • letters. print. Tree(); • z • • • c • b • a y x

Summary • Binary trees – one or two branches. – E. g. logical or arithmetic expression. Get/set methods data/left/right. Binary Search tree is a special case of a binary tree. Given the current node (according to compare. To) - all the left nodes are less than current node – all the right nodes are greater than current node

Concept of Binary Search Tree