Lecture 16 Multiway Search Trees Slides modified from






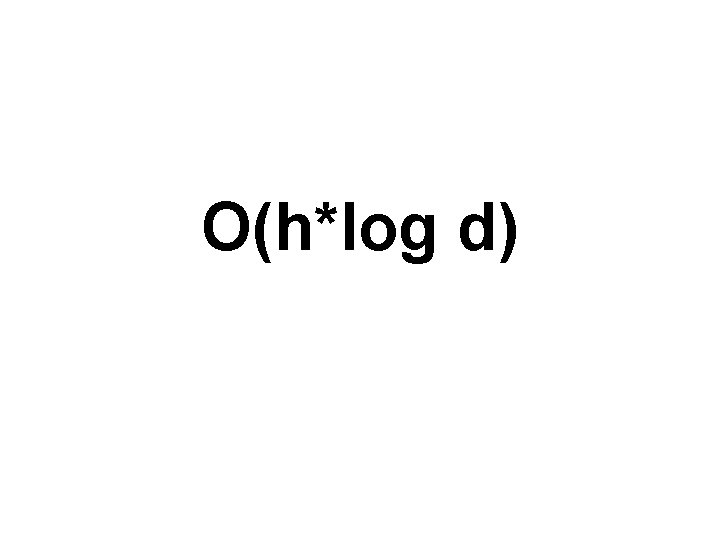








- Slides: 33

Lecture 16 Multiway Search Trees Slides modified from © 2010 Goodrich, Tamassia & by Prof. Naveen Garg’s Lectures

Ordered Maps So far • List/Array • BST • AVL Tree

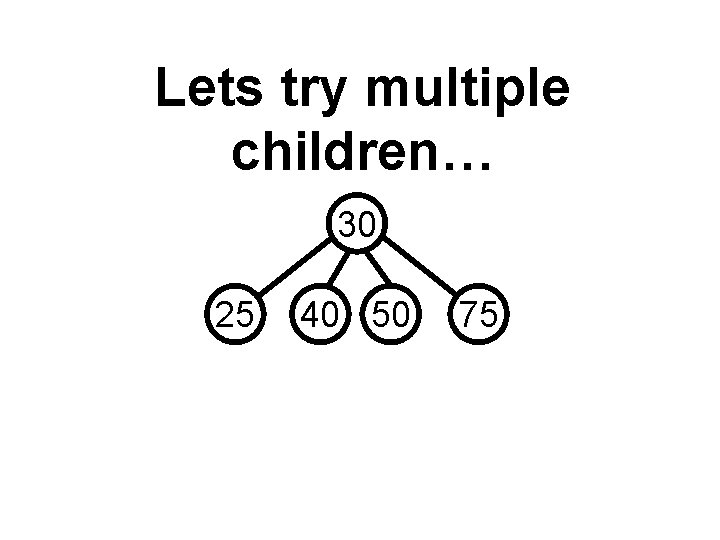
Lets try multiple children… 30 25 40 50 75

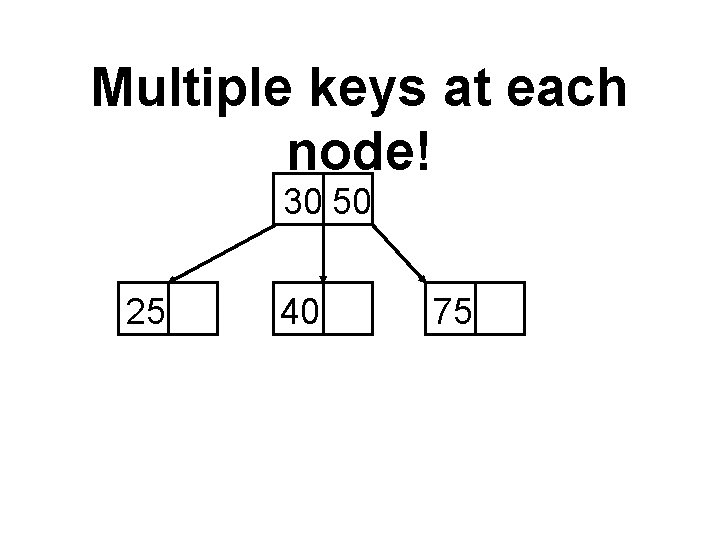
Multiple keys at each node! 30 50 25 40 75

How many keys do we need at a node to have d-way search tree? d-1

Confusion Points 1. nodes 2. keys 3. children

Multiway search tree with degree d! • internal nodes have at least 2 children and at max d children • each node stores upto d-1 items

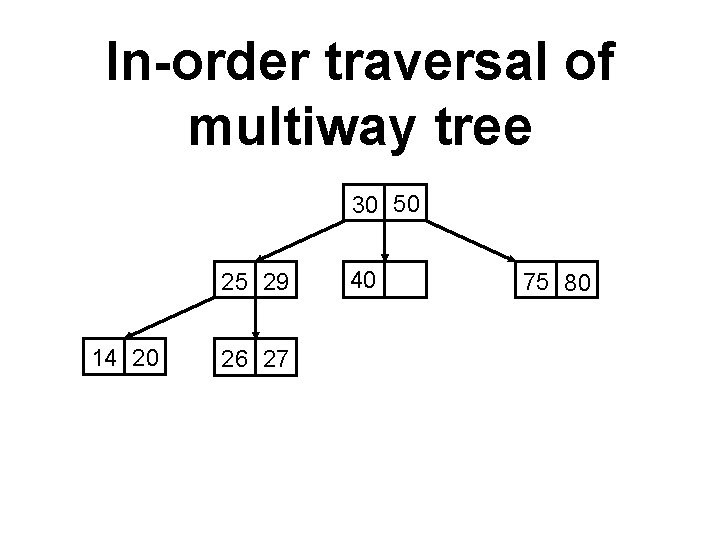
In-order traversal of multiway tree 30 50 25 29 14 20 26 27 40 75 80

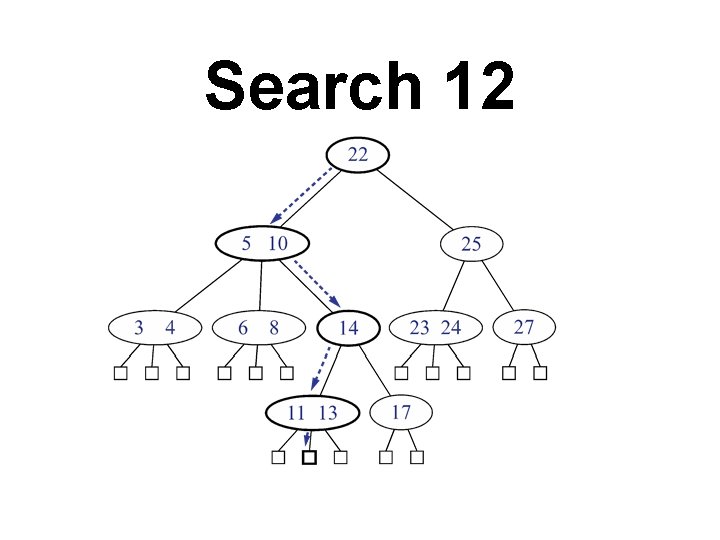
Search 12

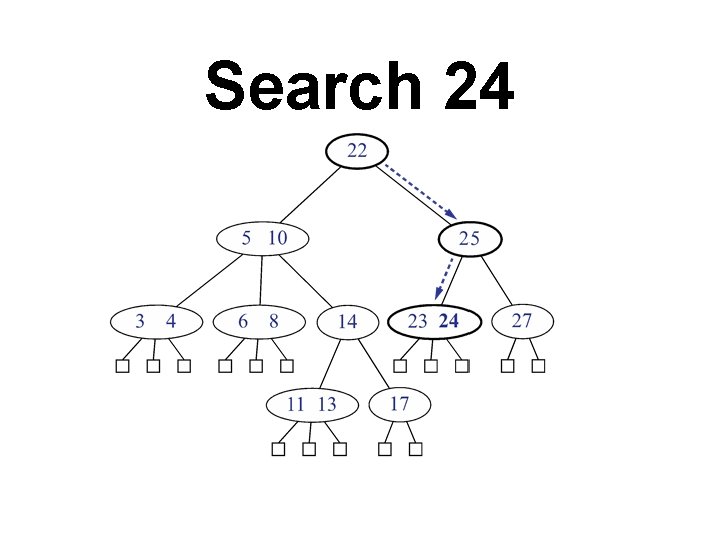
Search 24

What is the time complexity of search in a d-way search tree?
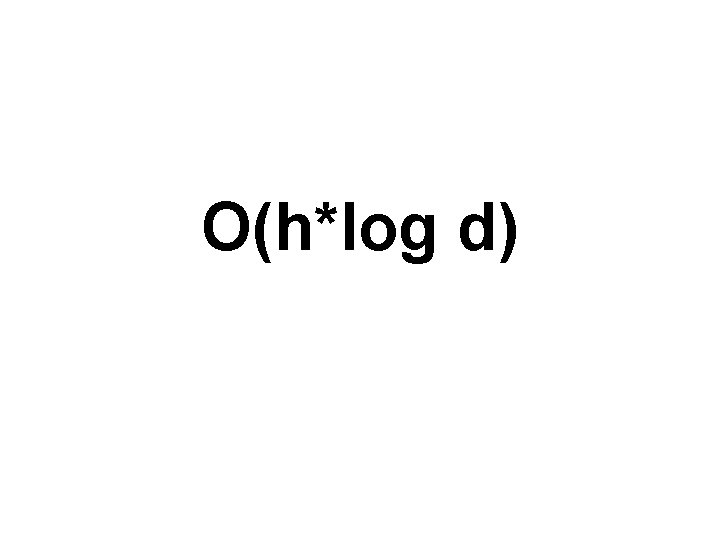
O(h*log d)

2 -4 Tree • a node can have 2 to 4 children • all leaf nodes are at the same level

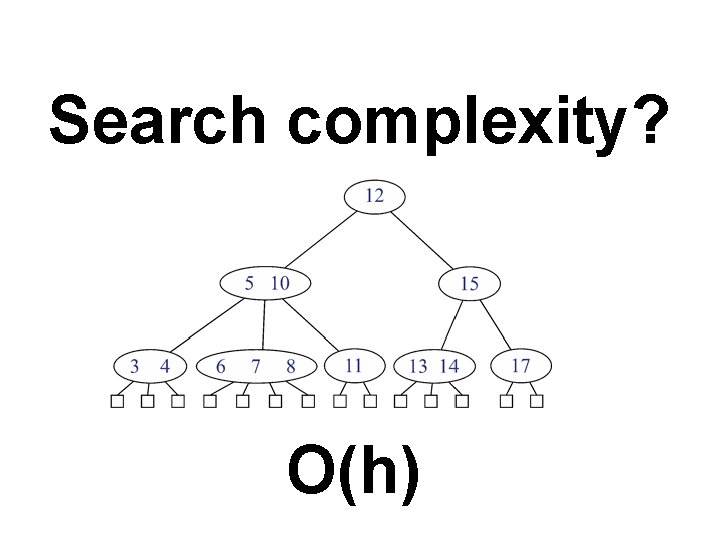
Search complexity? O(h)

Min & Max height (h)?

Minimum number of entries? h+1 n≥ 2 -1 h≤log 2(n+1)-1

Maximum number of entries? h+1 n≤ 4 -1 h≥log 4(n+1)-1

2 -4 Tree Height log 4(n+1)-1 ≤ h ≤ log 2(n+1)-1 1/2 log 2(n+1) ≤ h+1 ≤ log 2(n+1) O(log n)

Insert

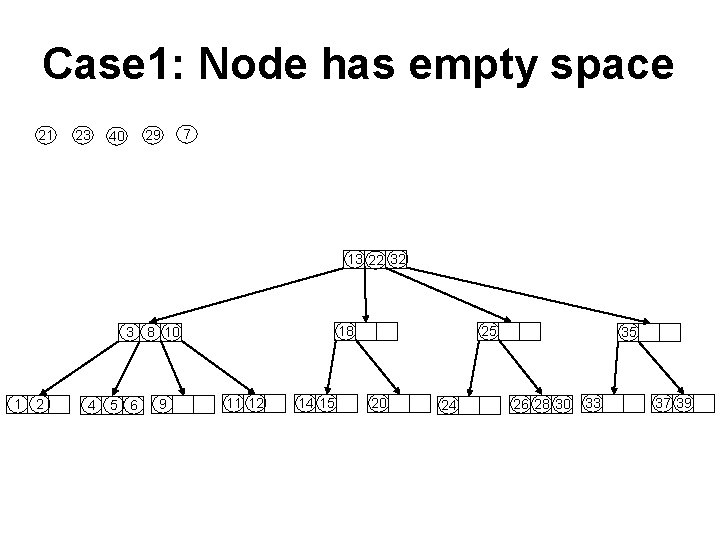
Case 1: Node has empty space 21 23 29 40 7 13 22 32 18 3 8 10 1 2 4 5 6 9 11 12 14 15 25 20 24 35 26 28 30 33 37 39

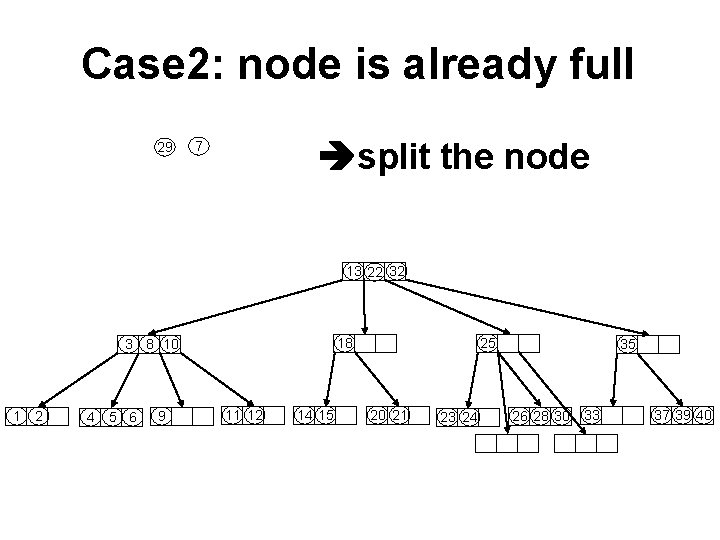
Case 2: node is already full 29 split the node 7 13 22 32 18 3 8 10 1 2 4 5 6 9 11 12 14 15 25 20 21 23 24 35 26 28 30 33 37 39 40

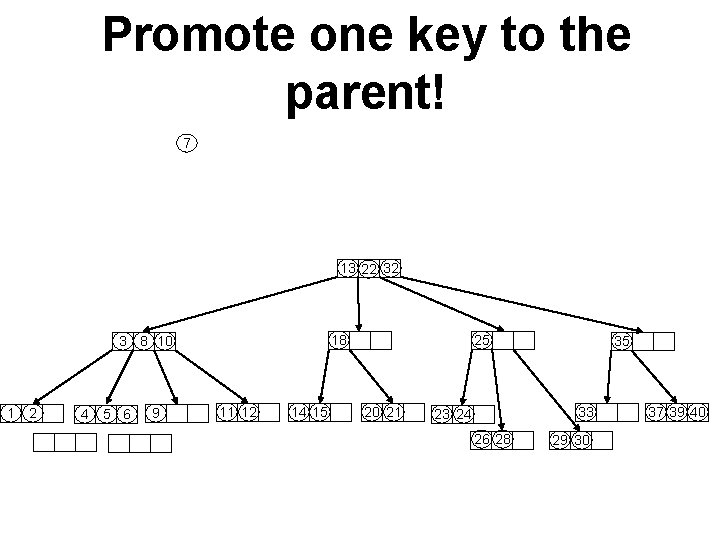
Promote one key to the parent! 7 13 22 32 18 3 8 10 1 2 4 5 6 9 11 12 14 15 25 20 21 35 33 23 24 26 28 29 30 37 39 40

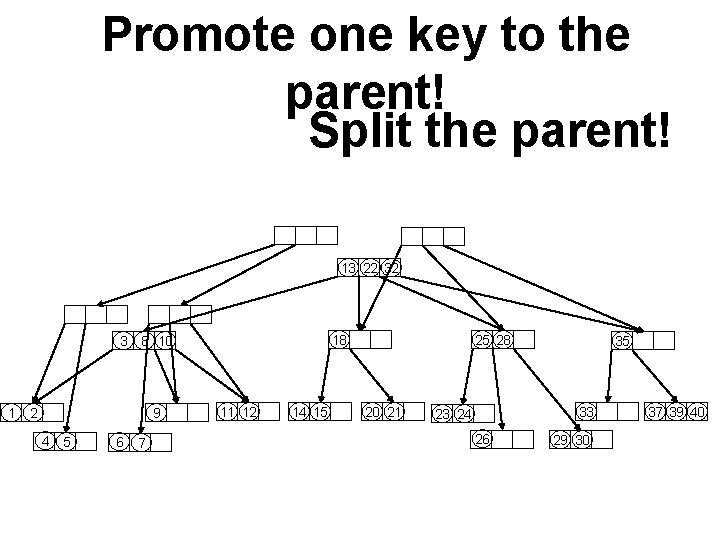
Promote one key to the parent! Split the parent! 13 22 32 18 3 8 10 1 2 9 4 5 6 7 11 12 14 15 25 28 20 21 35 33 23 24 26 29 30 37 39 40

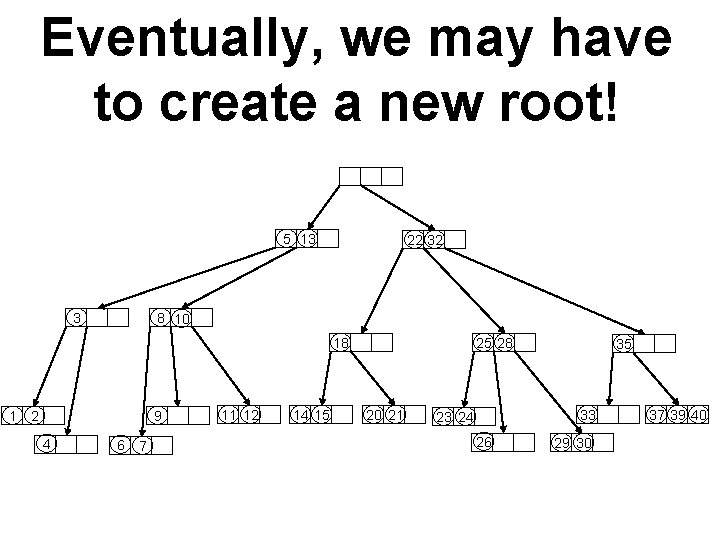
Eventually, we may have to create a new root! 5 13 3 22 32 8 10 18 1 2 9 4 6 7 11 12 14 15 25 28 20 21 35 33 23 24 26 29 30 37 39 40

Complexity of insert? • O(log n) to find the node • O(log n) node splits in the worst • Node split takes constant time o(log n)

Delete

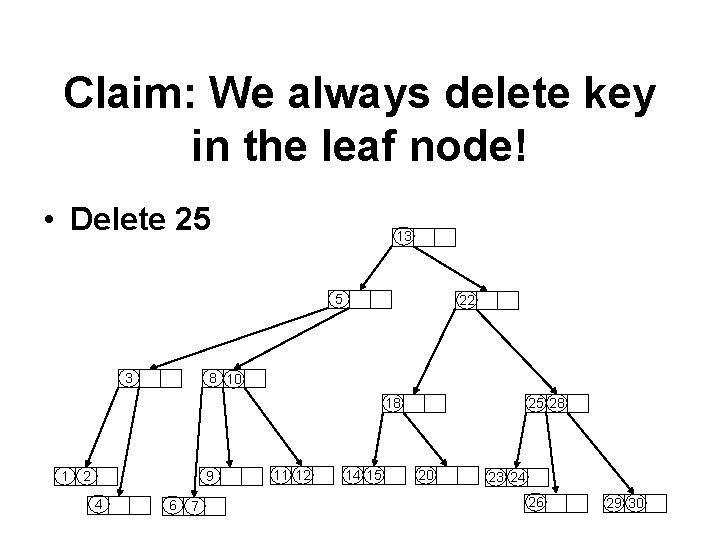
Claim: We always delete key in the leaf node! • Delete 25 13 5 3 22 8 10 18 1 2 9 4 6 7 11 12 14 15 25 28 20 23 24 26 29 30

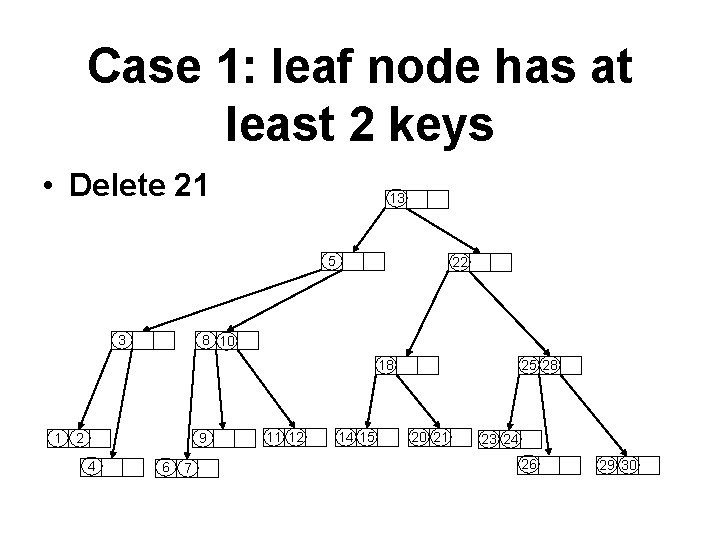
Case 1: leaf node has at least 2 keys • Delete 21 13 5 3 22 8 10 18 1 2 9 4 6 7 11 12 14 15 25 28 20 21 23 24 26 29 30

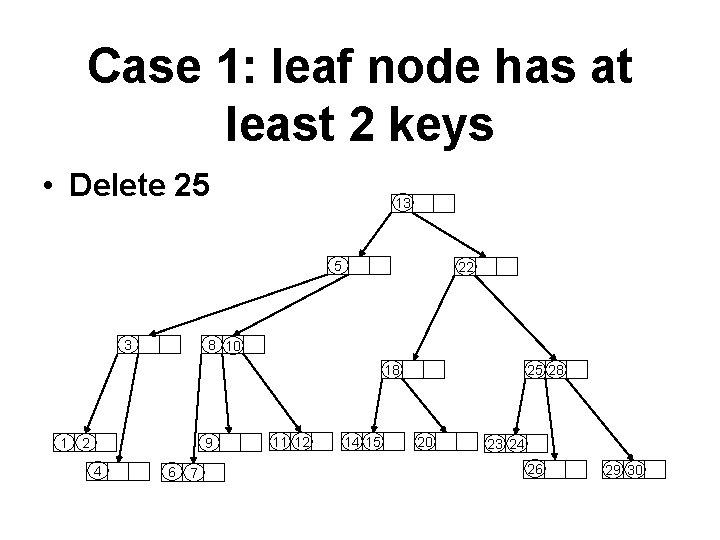
Case 1: leaf node has at least 2 keys • Delete 25 13 5 3 22 8 10 18 1 2 9 4 6 7 11 12 14 15 25 28 20 23 24 26 29 30

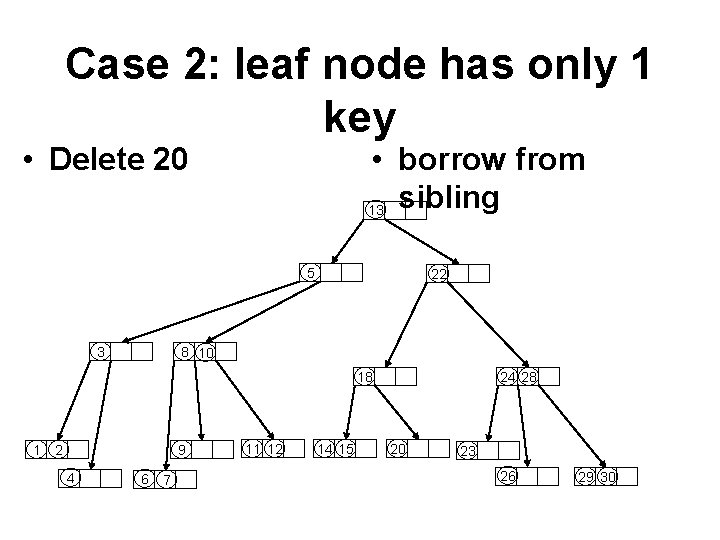
Case 2: leaf node has only 1 key • Delete 20 • borrow from 13 sibling 5 3 22 8 10 18 1 2 9 4 6 7 11 12 14 15 24 28 20 23 26 29 30

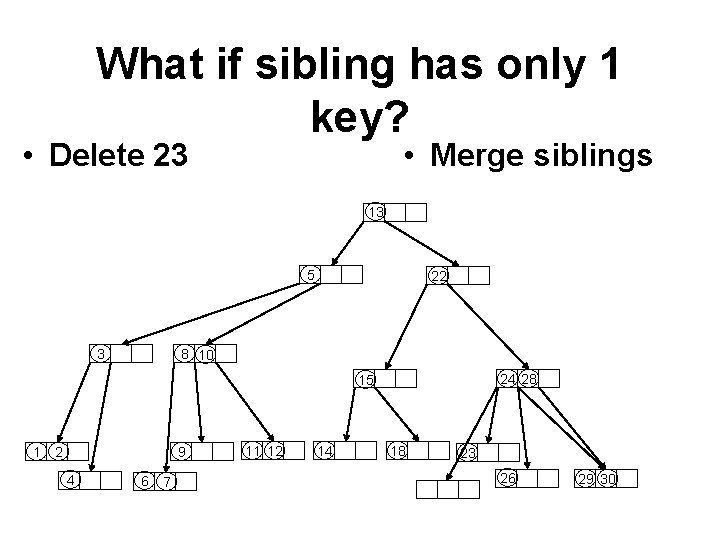
What if sibling has only 1 key? • Delete 23 • Merge siblings 13 5 3 22 8 10 24 28 15 1 2 9 4 6 7 11 12 14 18 23 26 29 30

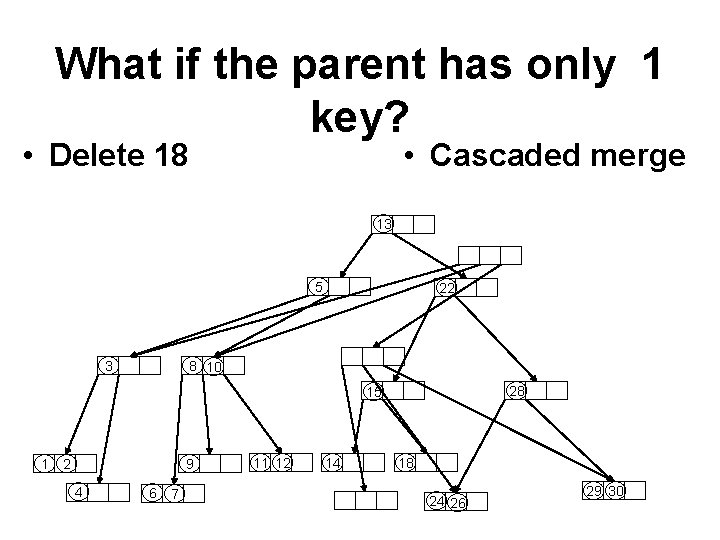
What if the parent has only 1 key? • Delete 18 • Cascaded merge 13 5 3 22 8 10 28 15 1 2 9 4 6 7 11 12 14 18 24 26 29 30

2 -4 Trees • The height of a (2, 4) tree is O(log n). • Search, insertion and deletion each take O(log n). • Pretty fundamental to the ideas of advanced trees such as Red-Black trees.