More Trees Multiway Trees and 2 4 Trees











- Slides: 25

More Trees Multiway Trees and 2 -4 Trees

Motivation of Multi-way Trees � Main memory vs. disk ◦ Assumptions so far: ◦ We have assumed that we can store an entire data structure in the main memory of a computer. ◦ What if we have more data than can fit in main memory? ◦ Meaning that we must have the data structure reside on disk. ◦ The rules of the game change, because the Big. Oh model doesn’t apply if all operations are not equal.

Motivation of Multi-way Trees �Main memory vs. disk ◦ Disk Accesses are incredibly expensive. ◦ 1 disk access is worth about 4, 000 instructions. ◦ (See the book for derivation) ◦ So we’re willing to do lots of calculations just to save disk accesses.

Motivation of Multi-way Trees For example: ◦ Suppose we want to access the driving records of the citizens of Florida. 10 million items. The Unbalanced Binary tree would be a disaster. Assume doesn’t fit in main memory. In the worst case, it has linear depth and could Assume in 1 sec, can require 10 mil disk execute 25 million accesses. instructions or perform 6 disk accesses. An AVL Tree In the typical case, it has a depth close to log N, log 10 mil ≈ 24 disk accesses,

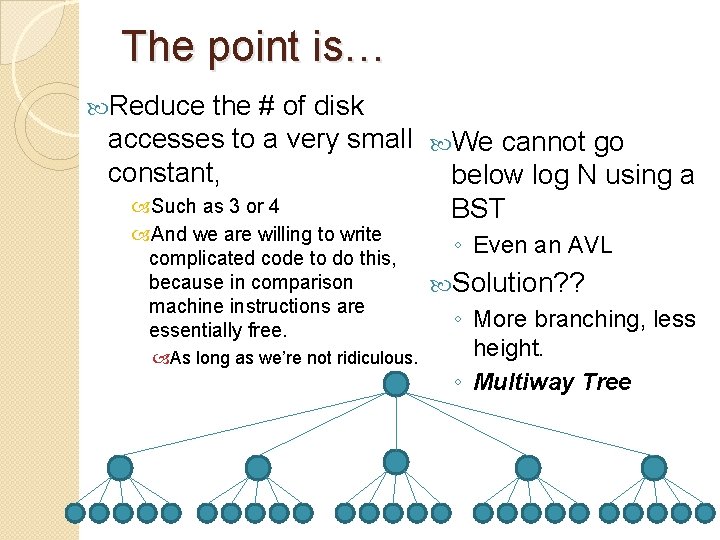
The point is… Reduce the # of disk accesses to a very small We cannot go constant, below log N using a Such as 3 or 4 BST And we are willing to write complicated code to do this, because in comparison machine instructions are essentially free. As long as we’re not ridiculous. ◦ Even an AVL Solution? ? ◦ More branching, less height. ◦ Multiway Tree

Multiway Tree (or B-tree in book) Multiway tree is similar to BST ◦ In a BST We need 1 key to decide which of 2 branches to take. ◦ In an Multiway tree We need M-1 keys to decide which branch to take, where M is the order of the Multiway tree. Also need to balance, Otherwise like a BST it could degenerate into a linked list. ◦ Here is a Multiway tree of Order 5:

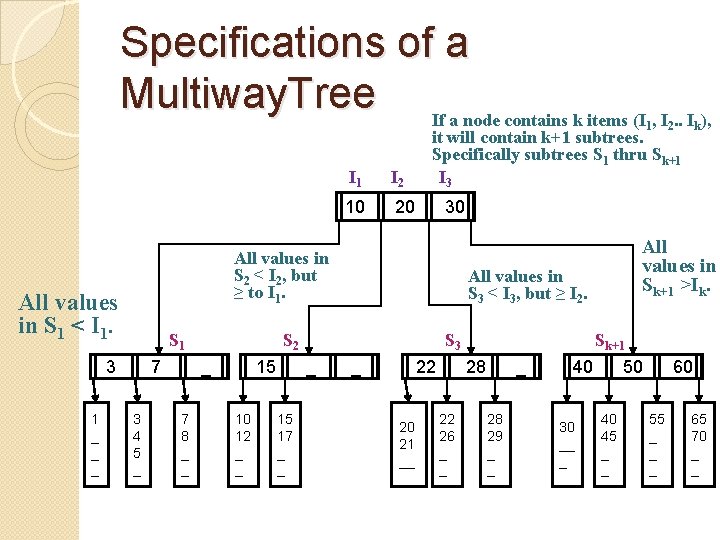
Specifications of a Multiway. Tree If a node contains k items (I , I. . I ), 1 I 2 10 20 S 1 3 7 3 4 5 _ 7 8 _ _ 15 10 12 _ _ S 3 _ 15 17 _ _ All values in Sk+1 >Ik. All values in S 3 < I 3, but ≥ I 2. S 2 _ _ 22 20 21 __ k 30 All values in S 2 < I 2, but ≥ to I 1. All values in S 1 < I 1. 1 _ _ _ I 1 2 it will contain k+1 subtrees. Specifically subtrees S 1 thru Sk+1 I 3 28 22 26 _ _ _ 28 29 _ _ Sk+1 40 50 30 __ _ 40 45 _ _ 60 55 _ _ _ 65 70 _ _

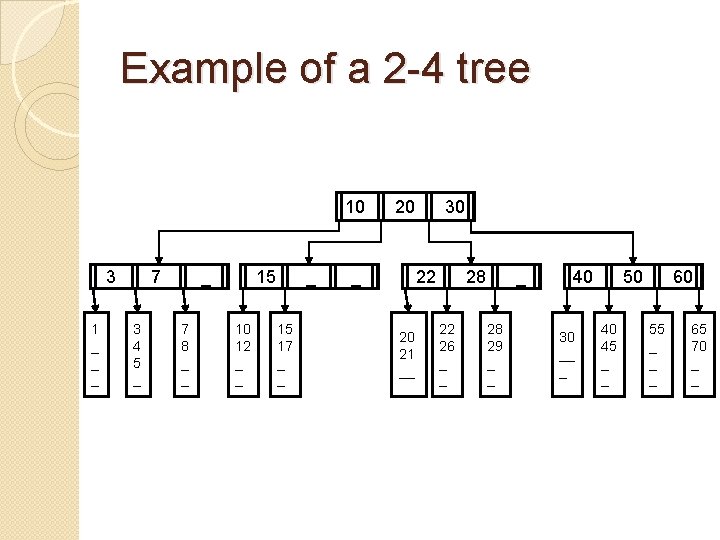
2 -4 Trees ◦ Specific type of multitree. 1) Every node must have in between 2 and 4 children. (Thus each internal node must store in between 1 and 3 keys) 2) All external nodes (the null children of leaf nodes) and leaf nodes have the same depth.

Example of a 2 -4 tree 10 3 1 _ _ _ 7 3 4 5 _ _ 7 8 _ _ 15 10 12 _ _ _ 15 17 _ _ 20 _ 30 22 20 21 __ 28 22 26 _ _ _ 28 29 _ _ 40 30 __ _ 50 40 45 _ _ 60 55 _ _ _ 65 70 _ _

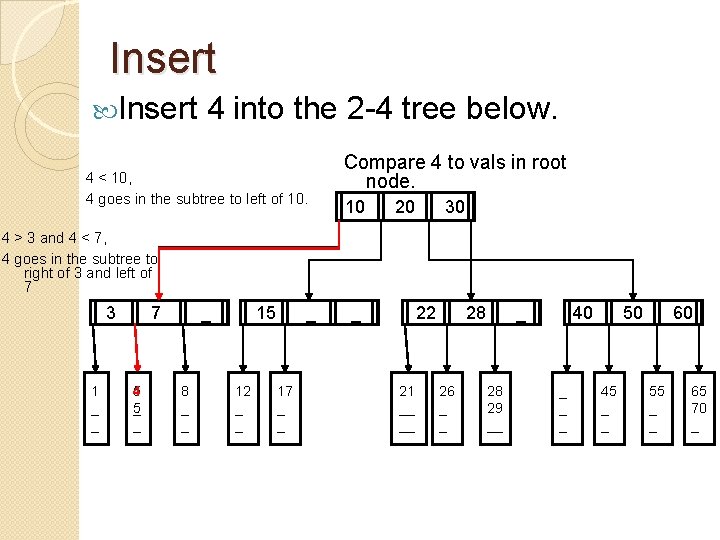
Insert 4 into the 2 -4 tree below. 4 < 10, 4 goes in the subtree to left of 10. Compare 4 to vals in root node. 10 20 30 4 > 3 and 4 < 7, 4 goes in the subtree to right of 3 and left of 7 3 1 _ _ 7 4 5 _ _ 8 _ _ 15 12 _ _ _ 17 _ _ _ 22 21 __ __ 28 26 _ _ _ 28 29 __ 40 _ _ _ 50 45 _ _ 60 55 _ _ 65 70 _

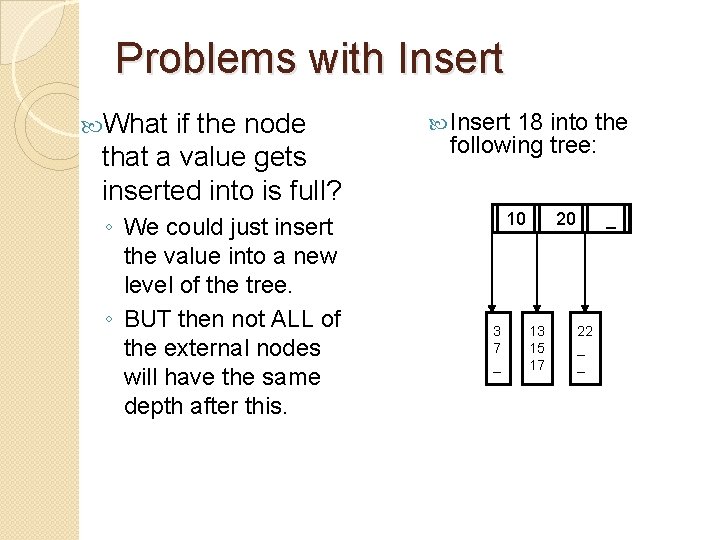
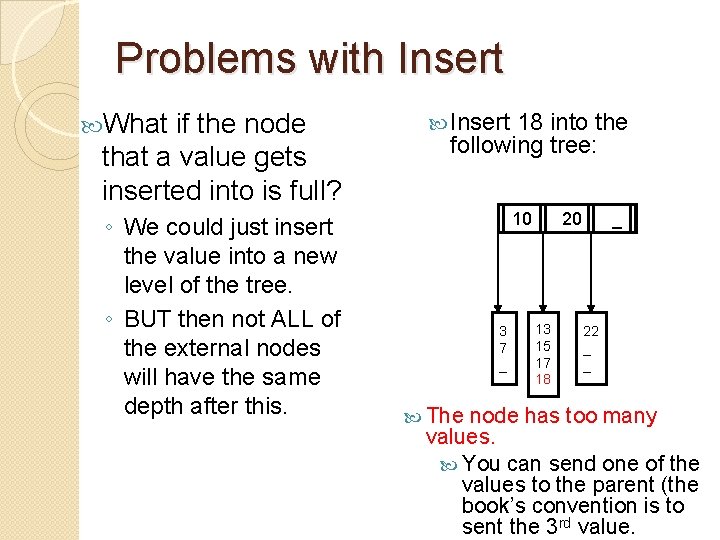
Problems with Insert What if the node that a value gets inserted into is full? ◦ We could just insert the value into a new level of the tree. ◦ BUT then not ALL of the external nodes will have the same depth after this. Insert 18 into the following tree: 10 3 7 _ 20 13 15 17 _ 22 _ _

Problems with Insert What if the node that a value gets inserted into is full? ◦ We could just insert the value into a new level of the tree. ◦ BUT then not ALL of the external nodes will have the same depth after this. Insert 18 into the following tree: 10 3 7 _ The 20 13 15 17 18 _ 22 _ _ node has too many values. You can send one of the values to the parent (the book’s convention is to sent the 3 rd value.

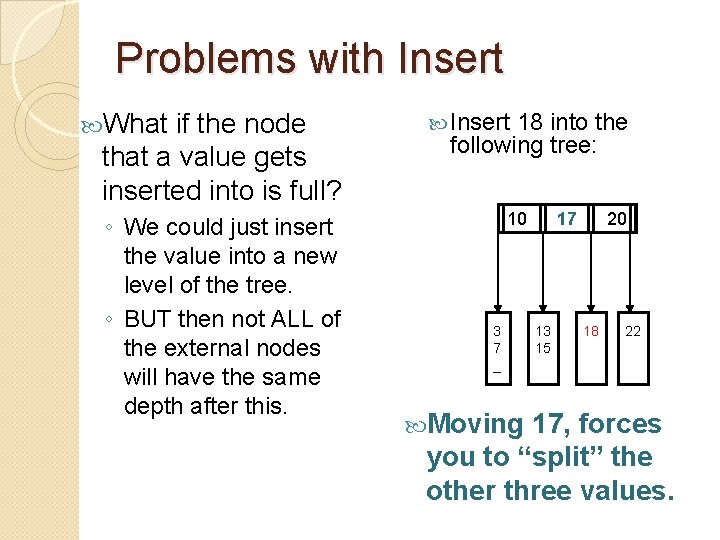
Problems with Insert What if the node that a value gets inserted into is full? ◦ We could just insert the value into a new level of the tree. ◦ BUT then not ALL of the external nodes will have the same depth after this. Insert 18 into the following tree: 10 3 7 _ Moving 17 13 15 _ 20 18 __ __ 22 _ _ 17, forces you to “split” the other three values.

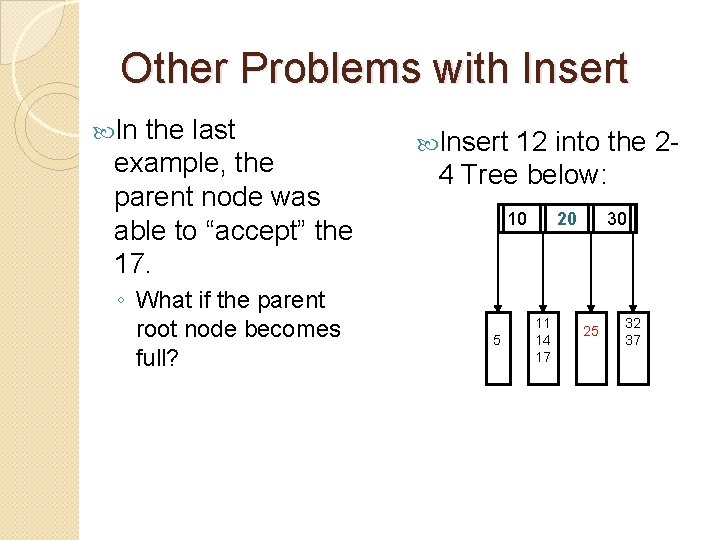
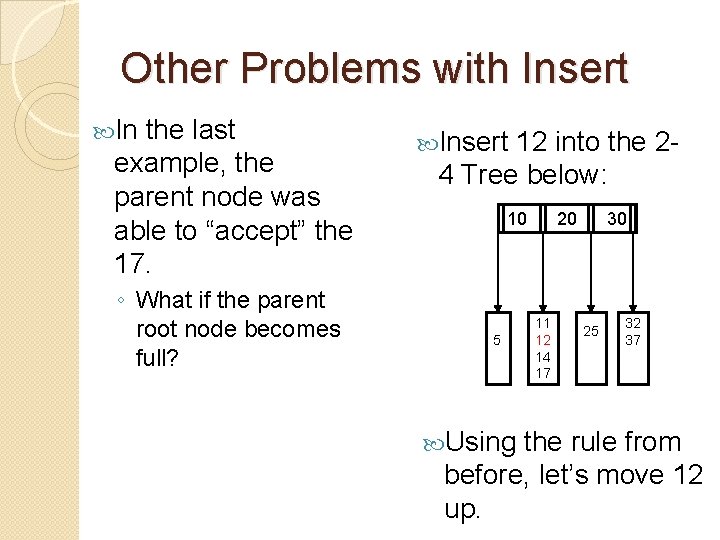
Other Problems with Insert In the last example, the parent node was able to “accept” the 17. ◦ What if the parent root node becomes full? Insert 12 into the 24 Tree below: 10 5 _ 20 11 14 17 _ 30 25 __ __ 32 37 _ _

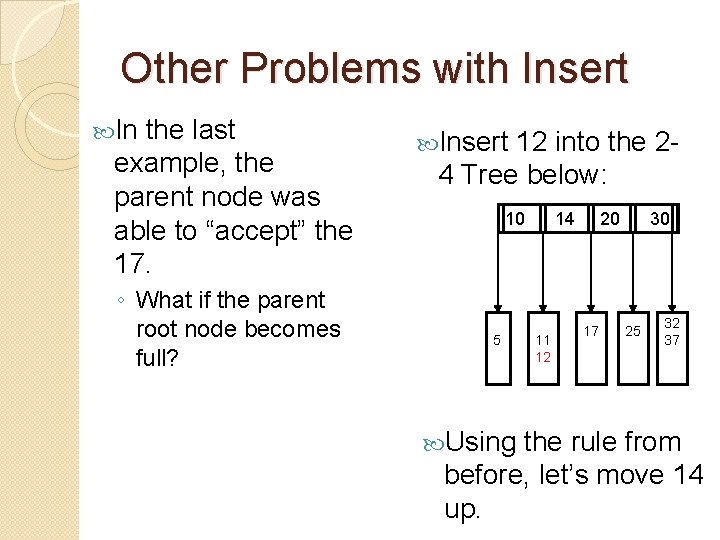
Other Problems with Insert In the last example, the parent node was able to “accept” the 17. ◦ What if the parent root node becomes full? Insert 12 into the 24 Tree below: 10 5 _ Using 20 11 12 14 17 30 25 __ __ 32 37 _ _ the rule from before, let’s move 12 up.

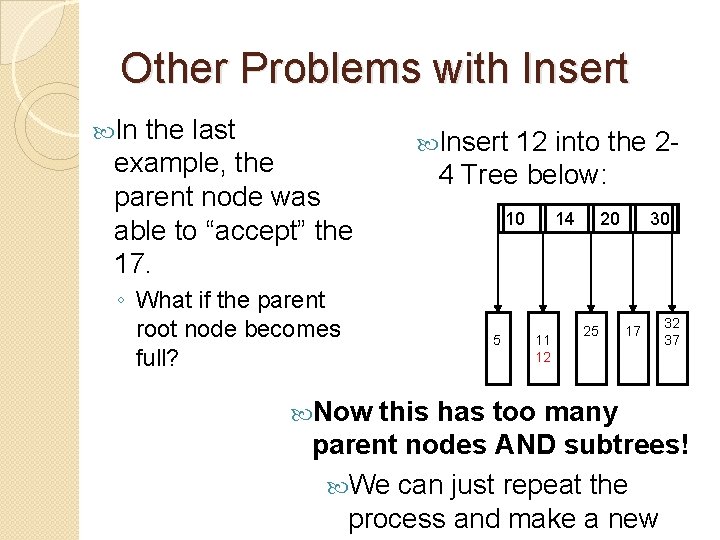
Other Problems with Insert In the last example, the parent node was able to “accept” the 17. ◦ What if the parent root node becomes full? Insert 12 into the 24 Tree below: 10 5 _ Using 14 11 12 20 17 __ __ 30 25 __ __ 32 37 _ _ the rule from before, let’s move 14 up.

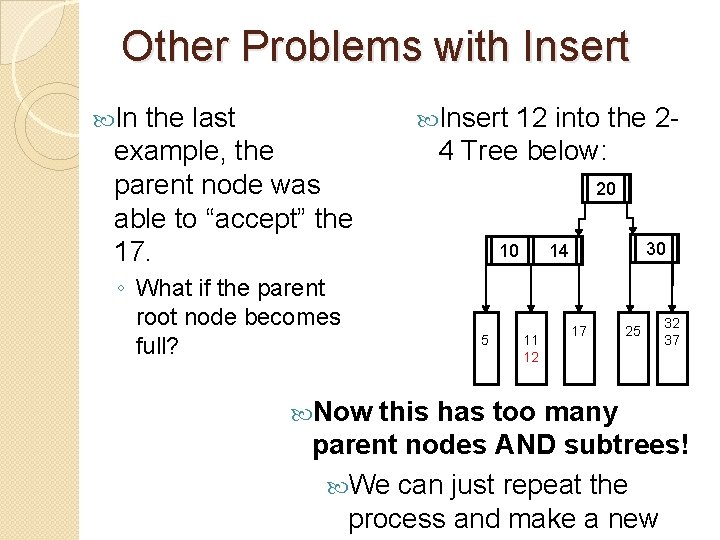
Other Problems with Insert In the last example, the parent node was able to “accept” the 17. ◦ What if the parent root node becomes full? Now Insert 12 into the 24 Tree below: 10 5 _ 14 11 12 20 25 __ __ 30 17 __ __ 32 37 _ _ this has too many parent nodes AND subtrees! We can just repeat the process and make a new

Other Problems with Insert In the last example, the parent node was able to “accept” the 17. ◦ What if the parent root node becomes full? Now Insert 12 into the 24 Tree below: 20 10 5 _ 30 14 11 12 17 __ __ 25 __ __ 32 37 _ _ this has too many parent nodes AND subtrees! We can just repeat the process and make a new

Deletion from a 2 -4 Tree Delete a non-leaf value ◦ Replace that value with the largest value in its left subtree Or smallest value in its right subtree.

Deletion from a 2 -4 Tree Delete a leaf node ◦ In the standard case: a value can simply be removed from a leaf node that stores more than one value. Requires no structural change. 10 20 30 Delete 5 5 7 _ 12 17 __ 23 27 35 35 _ _

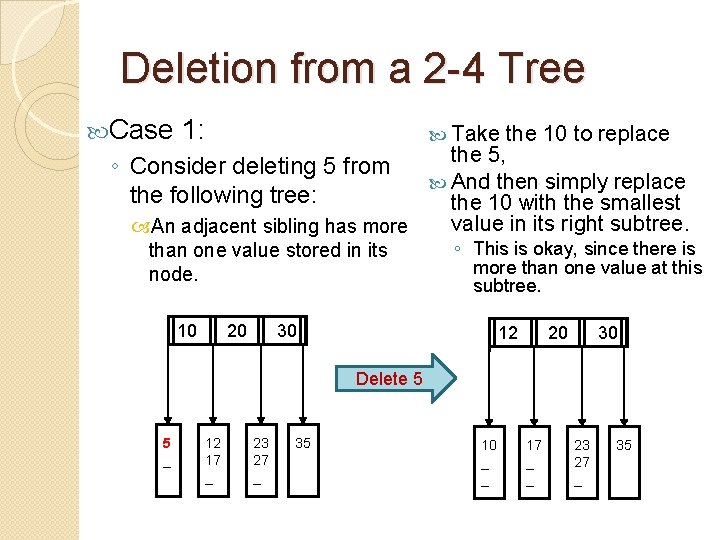
Deletion from a 2 -4 Tree BUT what if the leaf ◦ If you get rid of it, node has ONLY one value? then it would violate the 2 -4 property that all leaf nodes MUST be on the same height of the tree. Break up into 2 cases: 1) An adjacent sibling has more than one value stored in its node. 2) An adjacent sibling does NOT have more than one value stored in its node, and a fusion operation MUST be performed.

Deletion from a 2 -4 Tree Case 1: Take the 10 to replace the 5, And then simply replace the 10 with the smallest value in its right subtree. An adjacent sibling has more ◦ Consider deleting 5 from the following tree: than one value stored in its node. 10 20 ◦ This is okay, since there is more than one value at this subtree. 30 12 20 30 Delete 5 5 _ _ 12 17 __ 23 27 _ 35 _ _ 10 _ __ 17 _ __ 23 27 _ 35 _ _

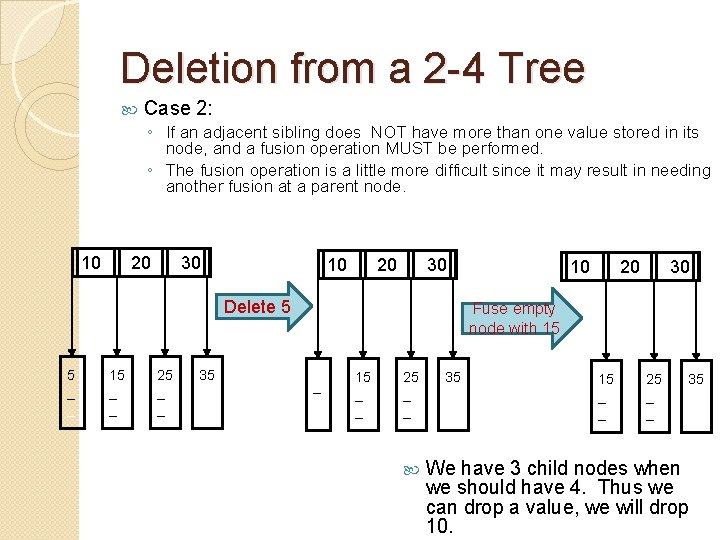
Deletion from a 2 -4 Tree Case 2: ◦ If an adjacent sibling does NOT have more than one value stored in its node, and a fusion operation MUST be performed. ◦ The fusion operation is a little more difficult since it may result in needing another fusion at a parent node. 10 20 30 Delete 5 5 _ _ 15 _ __ 25 _ _ 35 _ _ 10 20 30 Fuse empty node with 15 _ __ 25 _ _ 35 _ _ We have 3 child nodes when we should have 4. Thus we can drop a value, we will drop 10.

Deletion from a 2 -4 Tree Case 2: ◦ If an adjacent sibling does NOT have more than one value stored in its node, and a fusion operation MUST be performed. ◦ The fusion operation is a little more difficult since it may result in needing another fusion at a parent node. 10 20 30 Drop one parent into fused node 15 _ __ 25 _ _ 35 _ _ 10 15 __ 25 _ _ 35 _ _ We have 3 child nodes when we should have 4. Thus we can drop a value, we will drop 10.

Examples on the Board