Multiloop scattering amplitudes in maximally supersymmetric gauge and

Multi-loop scattering amplitudes in maximally supersymmetric gauge and gravity theories. Twistors, Strings and Scattering Amplitudes Durham August 24, 2007 Zvi Bern, UCLA C. Anastasiou, ZB, L. Dixon, and D. Kosower, hep-th/0309040 ZB, L. Dixon and V. Smirnov, hep-th/0505205 ZB, M. Czakon, L. Dixon, D. Kosower and V. Smirnov, hep-th/0610248 ZB, N. E. J. Bjerrum-Bohr, D. Dunbar, hep-th/0501137 ZB, L. Dixon , R. Roiban, hep-th/0611086 ZB, J. J. Carrasco, L. Dixon, H. Johansson, D. Kosower, R. Roiban, hep-th/0702112 ZB, J. J. Carrasco, H. Johansson , D. Kosower ar. Xiv: 0705. 1864 [hep-th] ZB, J. J. Carrasco, D. Forde, H. Ita and H. Johansson, ar. Xiv: 0707. 1035 [hep-th] 1

Outline Since the “twistor revolution” of a few years ago we have seen a very significant advance in our ability to compute scattering amplitudes. • QCD: multi-parton scattering for LHC – not discussed here. • Supersymmetric gauge theory: resummation of planar N = 4 super-Yang-Mills scattering amplitudes to all loop orders. • Quantum gravity: reexamination of standard wisdom on ultraviolet properties of quantum gravity. 2

Maximal Supersymmetry In this talk we will discuss high loop orders of scattering amplitudes in maximally supersymmetric gauge and gravity theories. • N = 4 super-Yang-Mills theory is most promising D = 4 gauge theory that we will likely be able to solve completely. • Maximally supersymmetric gravity theory is the most promising theory which may be UV finite. • Scattering amplitudes provide a powerful way to explore and confirm the Ad. S/CFT correspondence. 3

Twistors Expose Amazing Simplicity Penrose twistor transform: Early work from Nair Witten conjectured that in twistor–space gauge theory amplitudes have delta-function support on curves of degree: Leads to MHV rules Connected picture Disconnected picture Structures imply an amazing simplicity in the scattering amplitudes. Witten Roiban, Spradlin and Volovich Cachazo, Svrcek and Witten Gukov, Motl and Neitzke Bena Bern and Kosower This simplicity gives us good reason to believe that there is much more structure to uncover at higher loops. 4

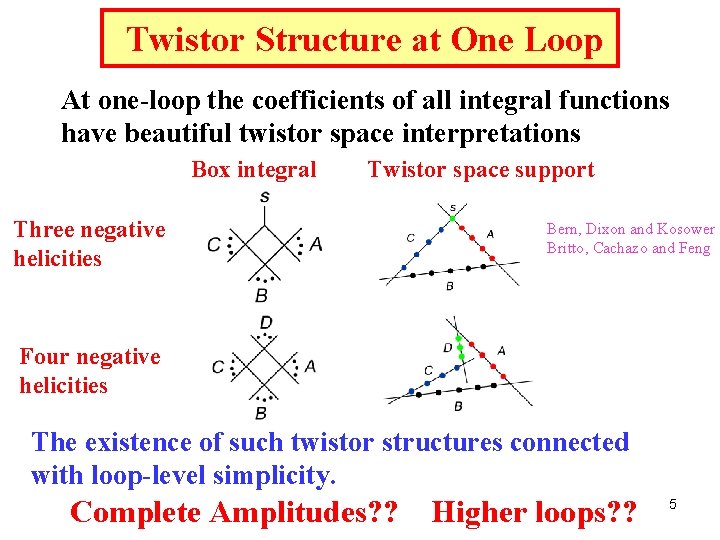
Twistor Structure at One Loop At one-loop the coefficients of all integral functions have beautiful twistor space interpretations Box integral Twistor space support Three negative helicities Bern, Dixon and Kosower Britto, Cachazo and Feng Four negative helicities The existence of such twistor structures connected with loop-level simplicity. Complete Amplitudes? ? Higher loops? ? 5

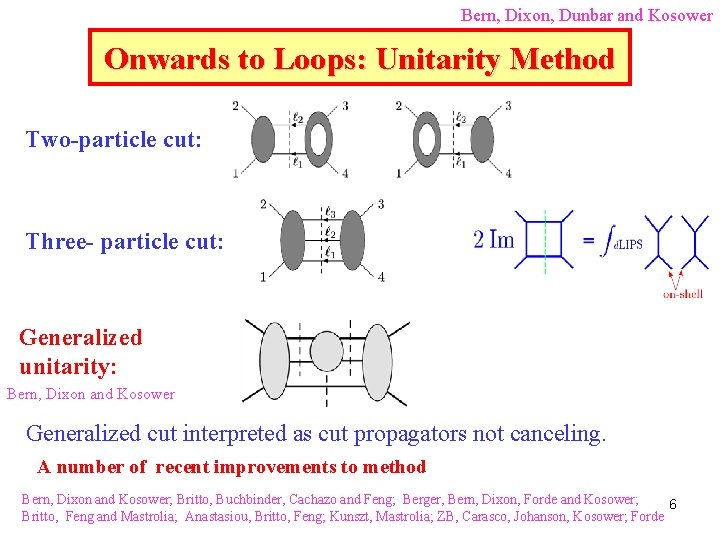
Bern, Dixon, Dunbar and Kosower Onwards to Loops: Unitarity Method Two-particle cut: Three- particle cut: Generalized unitarity: Bern, Dixon and Kosower Generalized cut interpreted as cut propagators not canceling. A number of recent improvements to method Bern, Dixon and Kosower; Britto, Buchbinder, Cachazo and Feng; Berger, Bern, Dixon, Forde and Kosower; 6 Britto, Feng and Mastrolia; Anastasiou, Britto, Feng; Kunszt, Mastrolia; ZB, Carasco, Johanson, Kosower; Forde

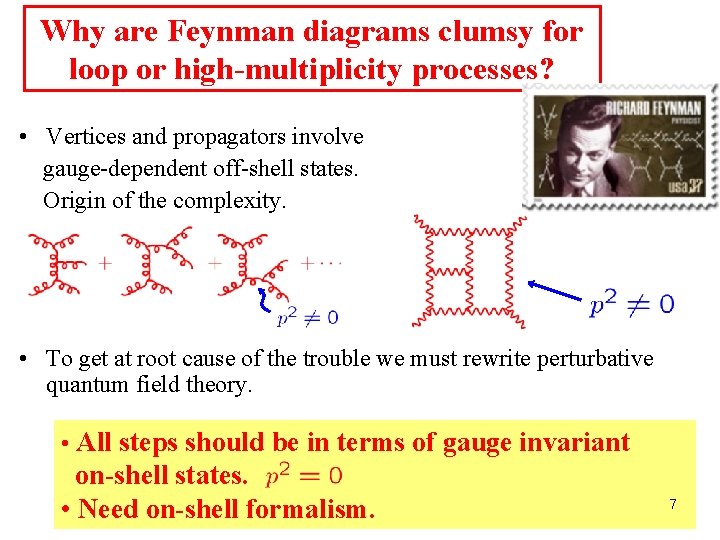
Why are Feynman diagrams clumsy for loop or high-multiplicity processes? • Vertices and propagators involve gauge-dependent off-shell states. Origin of the complexity. • To get at root cause of the trouble we must rewrite perturbative quantum field theory. • All steps should be in terms of gauge invariant on-shell states. • Need on-shell formalism. 7

N = 4 Super-Yang-Mills to All Loops Since ‘t Hooft’s paper thirty years ago on the planar limit of QCD we have dreamed of solving QCD in this limit. This is too hard. N = 4 s. YM is much more promising. • Heuristically, we expect magical simplicity in the scattering amplitude especially in planar limit with large ‘t Hooft coupling – dual to weakly coupled gravity in Ad. S space. Can we solve planar N = 4 super-Yang-Mills theory? Initial Goal: Resum amplitudes to all loop orders. As we heard at this conference we are well on our way to achieving this goal. 8 Talks from Alday, Volovich and Travaglini

N = 4 Multi-loop Amplitude Bern, Rozowsky and Yan Consider one-loop in N = 4: The basic D-dimensional two-particle sewing equation Applying this at one-loop gives Agrees with known result of Green, Schwarz and Brink. The two-particle cuts algebra recycles to all loop orders! 9

Loop Iteration of the Amplitude Four-point one-loop , N = 4 amplitude: To check for iteration use evaluation of two-loop integrals. Planar contributions. Obtained via unitarity method. Bern, Rozowsky, Yan Integrals known and involve 4 th order polylogarithms. V. Smirnov 10

Loop Iteration of the Amplitude The planar four-point two-loop amplitude undergoes Anastasiou, Bern, Dixon, Kosower fantastic simplification. is universal function related to IR singularities Thus we have succeeded to express two-loop four–point planar amplitude as iteration of one-loop amplitude. Confirmation directly on integrands. Cachazo, Spradlin and Volovich 11

Generalization to n Points Anastasiou, Bern, Dixon, Kosower Can we guess the n-point result? Expect simple structure. Trick: use collinear behavior for guess Bern, Dixon, Kosower Have calculated two-loop splitting amplitudes. Following ansatz satisfies all collinear constraints Valid for planar MHV amplitudes Confirmed by direct computation at five points! D=4– 2 Cachazo, Spradlin and Volovich 12 Bern, Czakon, Kosower, Roiban, Smirnov

Three-loop Generalization From unitarity method we get three-loop planar integrand: Bern, Rozowsky, Yan Use Mellin-Barnes integration technology and apply V. Smirnov Vermaseren and Remiddi hundreds of harmonic polylog identities: Bern, Dixon, Smirnov Answer actually does not actually depend on c 1 and c 2. Five-point calculation would determine these. 13

All-Leg All-Loop Generalization Why not be bold and guess scattering amplitudes for all loop and all legs (at least for MHV amplitudes)? • Remarkable formula from Magnea and Sterman tells us IR singularities to all loop orders. Checks construction. • Collinear limits gives us the key analytic information, at least for MHV amplitudes. One-loop All loops constant • Soft anomalous dimension • Or leading twist high spin anomalous dimension • Or cusp anomalous dimension 14

All-loop Resummation in N = 4 Super-YM Theory ZB, Dixon, Smirnov For MHV amplitudes: constant independent of kinematics. all-loop resummed amplitude IR divergences cusp anomalous dimension finite part of one-loop amplitude Wilson loop Gives a definite prediction for all values of coupling given the Beisert, Eden, Staudacher integral equation for the cusp anomalous dimension. See Roiban’s talk In a beautiful paper Alday and Maldacena confirmed this conjecture at strong coupling from an Ad. S string computation. See Alday’s and Volovoch’s talks Very suggestive link to Wilson loops even at weak coupling Drummond, Korchemsky, Sokatchev ; Brandhuber, Heslop, and Travaglini 15

Some Open Problems • What is the multi-loop structure of non-MHV amplitudes? Very likely there is an iteration and exponentiation. Input from strong coupling would be very helpful. • What is precice multi-loop twistor-space structure? Knowing this would be extremely helpful. • What is the twistor-space structure at strong coupling? • Is there an iteration and exponentiation for subleading color? • What happens for CFT cases with less susy? • Can we extract the spectrum of physical states from the exponentiated scattering amplitudes? 16

Quantum Gravity at High Loop Orders A key unsolved question is whether a finite point-like quantum gravity theory is possible. • Gravity is non-renormalizable by power counting. Dimensionful coupling • Every loop gains mass dimension - 2. At each loop order potential counterterm gains extra • As loop order increases potential counterterms must have either more R’s or more derivatives 17

Divergences in Gravity One loop: Vanish on shell vanishes by Gauss-Bonnet theorem Pure gravity 1 -loop finite (but not with matter) ‘t Hooft, Veltman (1974) Two loop: Pure gravity counterterm has non-zero coefficient: Goroff, Sagnotti (1986); van de Ven (1992) Any supergravity: is not a valid supersymmetric counterterm. Produces a helicity amplitude forbidden by susy. Grisaru (1977); Tomboulis (1977) The first divergence in any supergravity theory can be no earlier than three loops. 18

Why N = 8 Supergravity? • UV finiteness of N = 8 supergravity would imply a new symmetry or non-trivial dynamical mechanism. • The discovery of either would have a fundamental impact on our understanding of gravity. • High degree of supersymmetry makes this the most promising theory to investigate. • By N = 8 we mean ungauged Cremmer-Julia supergravity. No known superspace or supersymmetry argument prevents divergences from appearing at some loop order. Potential counterterm predicted by susy power counting Deser, Kay, Stelle (1977); Kaku, Townsend, van Nieuwenhuizen (1977); Deser and Lindtrom(1980); Kallosh (1981); Howe, Stelle, Townsend (1981). A three loop divergence was the widely accepted wisdom coming 19 from the 1980’s.

Where are the N = 8 Divergences? Depends on who you ask and when you ask. 3 loops: Conventional superspace power counting. Howe and Lindstrom (1981) Green, Schwarz and Brink (1982) Howe and Stelle (1989) Marcus and Sagnotti (1985) Dixon, Dunbar, Perelstein, 5 loops: Partial analysis of unitarity cuts. ZB, and Rozowsky (1998) If harmonic superspace with N = 6 susy manifest exists Howe and Stelle (2003) 6 loops: If harmonic superspace with N = 7 susy manifest exists Howe and Stelle (2003) 7 loops: If a superspace with N = 8 susy manifest were to exist. Grisaru and Siegel (1982) 8 loops: Explicit identification of potential susy invariant counterterm Kallosh; Howe and Lindstrom (1981) with full non-linear susy. 9 loops: Assume Berkovits’ superstring non-renormalization theorems can be naively carried over to N = 8 supergravity. Naïve extrapolation from 6 loops needed. Green, Vanhove, Russo (2006) Note: none of these are based on demonstrating a divergence. They are based on arguing susy protection runs out after some point. 20

Reasons to Reexamine This 1) The number of established counterterms in any supergravity 2) theory is zero. 2) Discovery of remarkable cancellations at 1 loop – the “no-triangle hypothesis”. ZB, Dixon, Perelstein, Rozowsky ZB, Bjerrum-Bohr and Dunbar; Bjerrum-Bohr, Dunbar, Ita, Perkins and Risager 3) Every explicit loop calculation to date finds N = 8 supergravity has identical power counting as in N = 4 super-Yang-Mills theory, which is UV finite. Green, Schwarz and Brink; ZB, Dixon, Dunbar, Perelstein, Rozowsky; Bjerrum-Bohr, Dunbar, Ita, Perkins. Risager; ZB, Carrasco, Dixon, Johanson, Kosower, Roiban. 4) Very interesting hint from string dualities. Chalmers; Green, Vanhove, Russo – Dualities restrict form of effective action. May prevent divergences from appearing in D = 4 supergravity. – Difficulties with decoupling of towers of massive states. See Green’s talk 5) Gravity twistor-space structure similar to gravity. Derivative of delta function support Witten; ZB, Bjerrum-Bohr, Dunbar 21

Gravity Feynman Rules Propagator in de Donder gauge: Three vertex has about 100 terms: An infinite number of other messy vertices Gravity looks to be a hopeless mess 22

Feynman Diagrams for Gravity Suppose we want to put an end to the speculations by explicitly calculating to see what is true and what is false: Suppose we wanted to check superspace claims with Feynman diagrams: If we attack this directly get terms in diagram. There is a reason why this hasn’t been evaluated previously. In 1998 we suggested that five loops is where the divergence is: This single diagram has terms prior to evaluating any integrals. More terms than atoms in your brain. 23

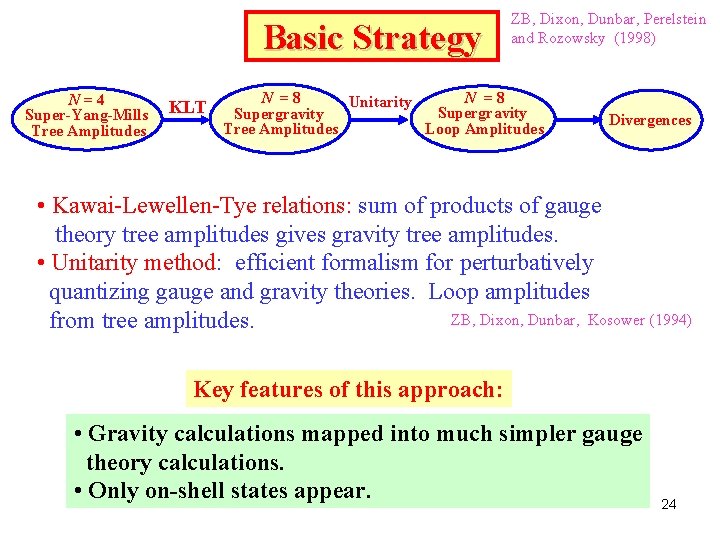
Basic Strategy N=4 Super-Yang-Mills Tree Amplitudes KLT ZB, Dixon, Dunbar, Perelstein and Rozowsky (1998) N =8 Unitarity Supergravity Loop Amplitudes Tree Amplitudes Divergences • Kawai-Lewellen-Tye relations: sum of products of gauge theory tree amplitudes gives gravity tree amplitudes. • Unitarity method: efficient formalism for perturbatively quantizing gauge and gravity theories. Loop amplitudes ZB, Dixon, Dunbar, Kosower (1994) from tree amplitudes. Key features of this approach: • Gravity calculations mapped into much simpler gauge theory calculations. • Only on-shell states appear. 24

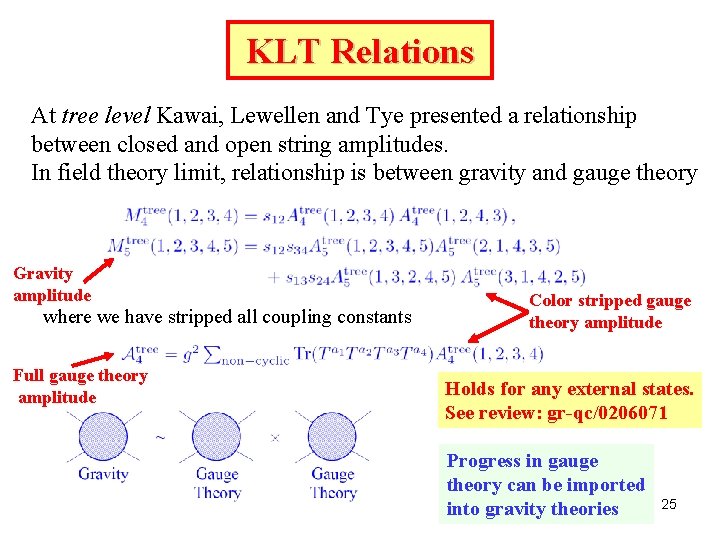
KLT Relations At tree level Kawai, Lewellen and Tye presented a relationship between closed and open string amplitudes. In field theory limit, relationship is between gravity and gauge theory Gravity amplitude where we have stripped all coupling constants Full gauge theory amplitude Color stripped gauge theory amplitude Holds for any external states. See review: gr-qc/0206071 Progress in gauge theory can be imported into gravity theories 25

N = 8 Power Counting To All Loop Orders From ’ 98 paper: • Assumed iterated 2 particle cuts give the generic UV behavior. • Assumed no cancellations with other uncalculated terms. No evidence was found that more than 12 powers of loop momenta come out of the integrals. Result from ’ 98 paper Elementary power counting gave finiteness condition: In D = 4 diverges for L L is number of loops. counterterm was expected in D = 4, for 5. 26

Additional Cancellations at One Loop Crucial hint of additional cancellation comes from one loop. Surprising cancellations not explained by any known susy mechanism are found beyond four points One derivative coupling Two derivative coupling One loop Two derivative coupling means N = 8 should have a worse power counting relative to N = 4 super-Yang-Mills theory. • Cancellations observed in MHV amplitudes. ZB, Dixon, Perelstein Rozowsky (1999) • “No-triangle hypothesis” — cancellations in all other amplitudes. ZB, Bjerrum-Bohr and Dunbar (2006) • Confirmed by explicit calculations at 6, 7 points. Bjerrum-Bohr, Dunbar, Ita, Perkins, Risager (2006) 27

No-Triangle Hypothesis One-loop D = 4 theorem: Any one loop massless amplitude is a linear combination of scalar box, triangle and bubble integrals with rational coefficients: • In N = 4 Yang-Mills only box integrals appear. No triangle integrals and no bubble integrals. • The “no-triangle hypothesis” is the statement that same holds in N = 8 supergravity. 28

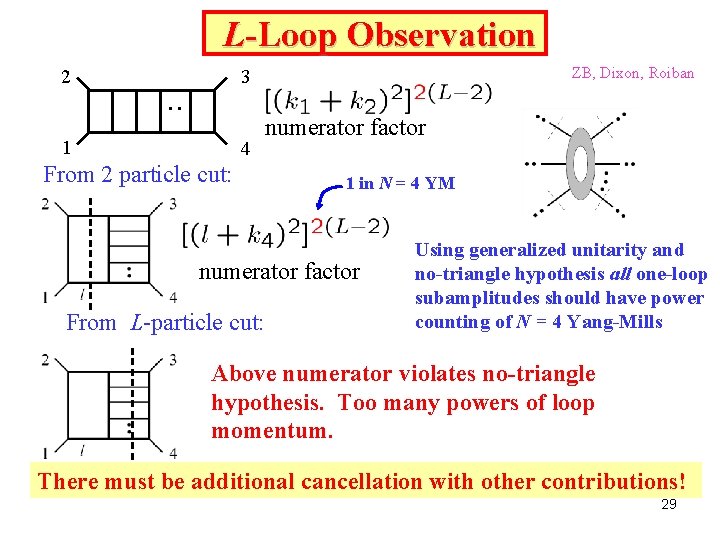
L-Loop Observation 2 ZB, Dixon, Roiban 3 . . 1 4 From 2 particle cut: numerator factor 1 in N = 4 YM numerator factor From L-particle cut: Using generalized unitarity and no-triangle hypothesis all one-loop subamplitudes should have power counting of N = 4 Yang-Mills Above numerator violates no-triangle hypothesis. Too many powers of loop momentum. There must be additional cancellation with other contributions! 29

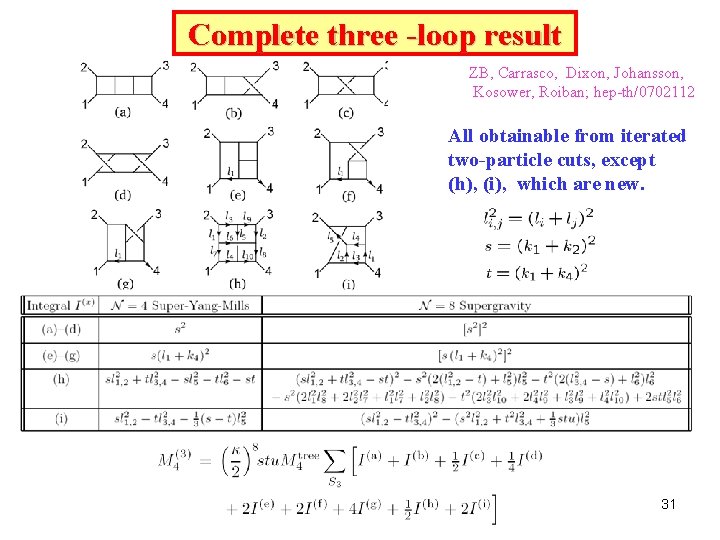
Complete Three-Loop Calculation ZB, Carrasco, Dixon, Johansson, Kosower, Roiban Besides iterated two-particle cuts need following cuts: For first cut have: reduces everything to product of tree amplitudes Use KLT supergravity super-Yang-Mills N = 8 supergravity cuts are sums of products of N = 4 super-Yang-Mills cuts 30

Complete three -loop result ZB, Carrasco, Dixon, Johansson, Kosower, Roiban; hep-th/0702112 All obtainable from iterated two-particle cuts, except (h), (i), which are new. 31

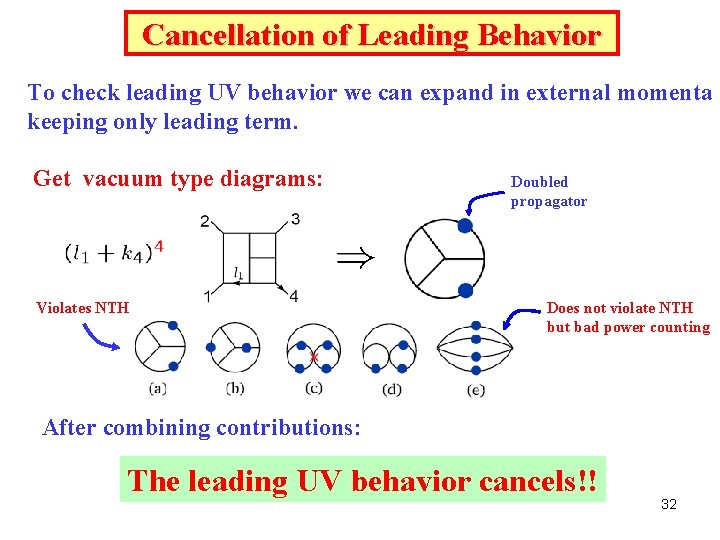
Cancellation of Leading Behavior To check leading UV behavior we can expand in external momenta keeping only leading term. Get vacuum type diagrams: Violates NTH Doubled propagator Does not violate NTH but bad power counting After combining contributions: The leading UV behavior cancels!! 32

Finiteness Conditions Through L = 3 loops the correct finiteness condition is (L > 1): “superfinite” in D = 4 • same as N = 4 super-Yang-Mills • bound saturated at L = 3 not the weaker result from iterated two-particle cuts: finite in D = 4 for L = 3, 4 (’ 98 prediction) Beyond L = 3, as already explained, from special cuts we have good reason to believe that the cancellations continue. All one-loop subamplitudes should have same UV power-counting as N = 4 super-Yang-Mills theory. 33

Origin of Cancellations? There does not appear to be a supersymmetry explanation for observed cancellations, especially if they hold to all loop orders, as we have argued. If it is not supersymmetry what might it be? 34

Tree Cancellations in Pure Gravity Unitarity method implies all loop cancellations come from tree amplitudes. Can we find tree cancellations? You don’t need to look far: proof of BCFW tree-level on-shell recursion relations in gravity relies on the existence such Britto, Cachazo, Feng and Witten; cancellations! Susy not required Bedford, Brandhuber, Spence and Travaglini Cachazo and Svrcek; Benincasa, Boucher-Veronneau and Cachazo Consider the shifted tree amplitude: How does ? behave as Proof of BCFW recursion requires 35

Loop Cancellations in Pure Gravity ZB, Carrasco, Forde, Ita, Johansson Powerful new one-loop integration method due to Forde makes it much easier to track the cancellations. Allows us to link one-loop cancellations to tree-level cancellations. Observation: Most of the one-loop cancellations observed in N = 8 supergravity leading to “no-triangle hypothesis” are already present in non-supersymmetric gravity. Susy cancellations are on top of these. n legs Maximum powers of Loop momenta Cancellation generic to Einstein gravity Cancellation from N = 8 susy Proposal: This continues to higher loops, so that most of the observed N = 8 multi-loop cancellations are not due to susy but in fact are generic to gravity theories! 36

What needs to be done? • N = 8 four-loop computation. Can we demonstrate that fourloop N = 8 amplitude has the same UV power counting as N = 4 super-Yang-Mills? Certainly feasible. • Can we construct a proof of perturbative UV finiteness of N = 8? Perhaps possible using unitarity method – formalism is recursive. • Investigate higher-loop pure gravity power counting to study cancellations. (It does diverge. ) Goroff and Sagnotti; van de Ven • Twistor structure of gravity loop amplitudes? • Link to a twistor string description of N = 8? Bern, Bjerrum-Bohr, Dunbar Abou-Zeid, Hull, Mason • Can we find other examples with less susy that may be finite? Guess: N = 6 supergravity theories will be perturbatively finite. 37

Summary • Twistor-space structures tell us gauge theory and gravity amplitudes are much simpler than previously anticipated. • Unitarity method gives us a powerful means for constructing multi-loop amplitudes. • Resummation of N = 4 MHV s. YM amplitudes – match to strong coupling! • At four points through three loops, established N = 8 supergravity has same power counting as N = 4 Yang-Mills. • Proposed that most of the observed N = 8 cancellations are present in generic gravity theories, with susy cancellations on top of these. • N = 8 supergravity may be the first example of a unitary point-like perturbatively UV finite theory of quantum gravity in D = 4. Proof is an open challenge. 38

Extra Transparencies 39

Non-trivial confirmation Method is designed to give same results as Feynman diagrams. Examples: 1. Two-loop-four gluon QCD amplitudes ZB, De Frietas, Dixon – matches results of Glover, Oleari and Tejeda-Yeomans 2. Four-loop cusp anomalous dimension in N = 4 s. YM – Beisert, Eden and Staudacher equation matches result. ZB, Czakon, Dixon, Kosower, Smirnov see Beisert’s talk 3. Resummation of 1, 2, 3 loop calculations to all loop order in N = 4 super-Yang-Mills theory Anastasiou, ZB, Dixon, Kosower; ZB, Dixon, Smirnov – matches the recent beautiful strong coupling construction of Alday and Maldacena. see Alday’s talk 40

Opinions from the 80’s We have not shown that a three-loop counterterm is not present in N > 4, although it is tempting to conjecture that this may be the case. Howe and Lindstrom (1981) If certain patterns that emerge should persist in the higher orders of perturbation theory, then … N = 8 supergravity in four dimensions would have ultraviolet divergences Green, Schwarz, Brink (1982) starting at three loops. Unfortunately, in the absence of further mechanisms for cancellation, the analogous N = 8 D = 4 supergravity theory would seem set to diverge at the three-loop order. Howe, Stelle (1984) There are no miracles… It is therefore very likely that all supergravity theories will diverge at three loops in four dimensions. … The final word on these issues may have to await further explicit calculations. Marcus, Sagnotti (1985) Widespread agreement that N = 8 supergravity should diverge at 3 loops 41

Comments on Higher Loops Rule of thumb: If we can compute N = 4 Yang-Mills to a given order we can do the same for N = 8 supergravity. We obtained the planar N = 4 YM amplitude at 5 loops: ZB, Carrasco, Johansson, Kosower Origin of claim that even 5 loop N = 8 supergravity is feasible. 42

What’s New? • In the 1960’s unitarity and analyticity widely used. • However, not understood how to use unitarity to reconstruct complete amplitudes with more than 2 kinematic variables. A(s, t ) Mandelstam representation Double dispersion relation Only 2 to 2 processes. With unitarity method we can build arbitrary amplitudes at any loop order from tree amplitude. Bern, Dixon, Dunbar and Kosower A(s 1 , s 2 , s 3 , . . . ) Unitarity method builds loops from tree ampitudes. 43

Other technical difficulties in the 60’s: • Non-convergence of dispersion relations. • Ambiguities or subtractions in the dispersion relations. • Confusion when massless particles present. • Inability to reconstruct rational functions with no branch cuts. The unitarity method overcomes these difficulties by (a) Using dimension regularization to make everything well defined. (b) Bypassing dispersion relations by writing down Feynman representations giving both real and 44 imaginary parts.