Scattering amplitudes for measuring the momentum and position



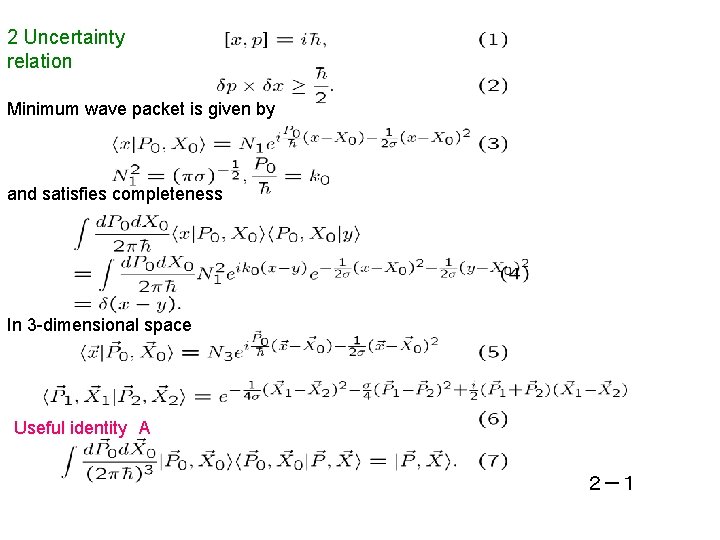






















- Slides: 26

Generalized S-Matrix in Mixed Representation Scattering amplitudes for measuring the momentum and position of particles K. Ishikawa (Hokkaido ) T. Shimomura (Saitama)

Scattering of Wave packets 1 Scattering of Initial and final states of definite values of position and momentum. 2 time development of wave packets 2 -1: one wave packet travels in space and spreads. : matrix elements of wave packets 3 generalized many–body scattering : field theory 3 -1: field expansion 3 -2: scattering amplitude 4 implications 4 -1: neutrino reactions 0 5 summary

1 introduction • In certain experiments, particle’ s momentum and position are measured. • We define and study momentum and position dependent scattering amplitude. • In order to define a position of a state, we should not use the eigenstate of momentum. • Wave packet is an approximate eigenstate of position and momentum. So we use the wave packet. • Wave packet spreading is important. 1
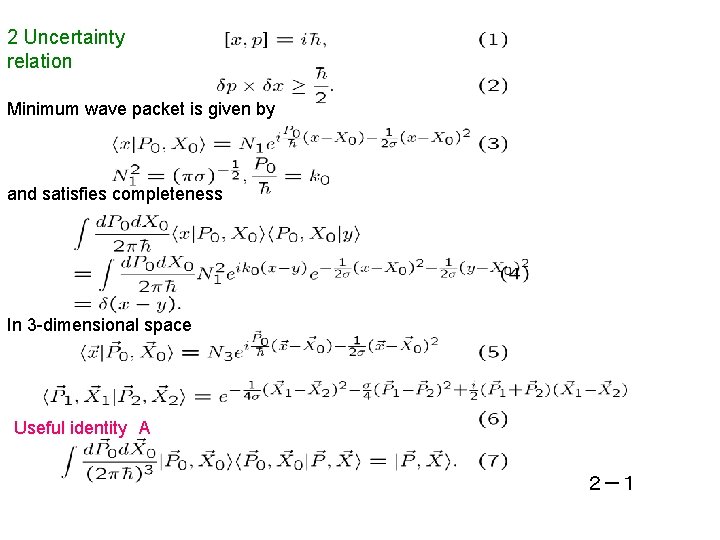
2 Uncertainty relation Minimum wave packet is given by and satisfies completeness In 3 -dimensional space Useful identity A 2-1

Evolution of wave packet : energy E(p) Momentum representation Coordinate representation is obtained by Fourier tr. Is small, then it travels with group velocity 2-2

Is large, then wave packet spreads Stationary phase approximaton is applied, Solution is Integral over p around px, then wave function is obtained as x x Widths in longitudinal and transverse directions are 2-3

Wave function’s phase Normalization’s maxima( use X 1, P 1 for X 0, P 0) Position x in term of P 0 is Neighbors of 2-4

Wave function depends on the position , x Spreading of wave packet is, Velocity of spreading New uncertainty of spreading velocities 2-5

3 Field theory momentum and Field expansion in mixed representation 3-1

Operator ‘s commutation relation and the completeness of generalized states satisfy commutation relation Multiply I’ to we have, using commutation relations and identity A, Hence I’ is unity 3-2

Generalized scattering amplitude depend, generally, on momentum, position, and wave packet’s size Differential probability depends on momentum, position, and wave packet’s size : Total probability does not depend on wave packet’s size 3-3

S-matrix Theorem 1: Integrated probability is independent of wave packet size Theorem 2: Total probability is unity 3-4

Few-body scattering Interaction regions in amplitude is found from, Gaussian function of x and t Center position 3-5 Time and space areas

Measurement dependence of interaction areas One σ Different σ Example 1: particle 1 is measured Example 2: particle 1 and 2 are measured > velocity dependent extension 3-6

short distance scattering amplitude Probability Classical trajectory 3-7

probability Position integration Momentum dependence 3-8

Long distance scattering Stationary phase 3-9

Integrate over x, then the propagator is replaced by 3-10

4 Solar neutrino and moon Effective interaction. 4-1

Solving wave equation (plain wave) for an uniform spherical potential V (x) : weak potential with large scale ( moon ) 解 Parameters for the moon 4-2

is neutrino wave packet ? Size of wave packet Sun-earth assumption Moon-earth Moon radius Interference may be expected 4-3

Wave functions Phase is written as 4-4

Magnitude of phase Overlap of in- and out- going waves 4-5

Interference of incoming wave with the moon potential and outgoing wave 4-6

• Reference , (1)K. Ishikawa and T. Shimomura, “ generalized S-Matrix in mixed representation” , Prog. of Theor. Phys. , 114, n 6(2005) (2)K. I and T. Shimomura, ” Coherent lunar effect of solar neutrino, HEP preprint 5-1

Summary 1. Wave packet is a useful state to study the scattering phenomena in which the momentum and position are measured. 2. Spreading of wave packets is important in some experiments. 3. Measurement of the momentum and position could supply new information on physical systems. 4. The present formalism will be useful in precision experiments and others. 5-2