Morphological Simplification Jason Williams and Jarek Rossignac GVU

Morphological Simplification Jason Williams and Jarek Rossignac GVU Center, IRIS Cluster, and College of Computing Georgia Institute of Technology www. cc. gatech. edu/~jarek NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 1

Overarching objective SIMPLIFICATION Understand what it means to simplify a shape or behavior Develop explicit mathematical formalisms independently of any particular domain or representation not stated as the result of some algorithmic process Propose practical implementations MULTI-SCALE ANALYSIS Explore the possibility of analyzing the evolution of a shape or behavior, as it is increasingly simplified, so as to understand its morphological structure and identify/measure its features identify features of interior, boundary, exterior assess their resilience to simplification NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 2

Complexity measures for 2 D shapes Many measures of complexity are useful in different contexts: • Visibility: Convex, star… number of guards needed • Stabbing: Number of intersections with “random” ray • Wiggles: energy in high frequency Fourier coefficients • Algebraic: Polynomial degree of bounding curves • Fidelity: accuracy required (Hausdorff, area preservation) • Processing: Number of bounding elements • Transmission: compressed file size • Fractal: Fractal dimension • Kolmogorov: Length of data and program We focus primarily on morphological ones: • Sharpness: curvature statistics • Smallest feature size: distance between non adjacent parts of boundary • Topological: Number of components and holes • Non-roundness: perimeter 2 /Area NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 3

What do we simplify and how much? Simplification replaces a shape by a simpler one • What do we mean by “simpler”? • Informally, we want to – Remove details • Reduce sharpness and wiggles • Eliminate small components and holes • Hence increase the smallest feature size – Shorten (tighten) the perimeter • While minimizing local changes in density – Ratio of interior points per square unit • How much do we want to simplify – We want to be able to use a geometric measure, r, to specify which of the details should be simplified and how – What does the measure mean? What is the size of a detail? NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 4

Restricting simplification to a tolerance zone • We want to restrict all changes to the envelop: tight zone around the boundary b. S of the shape S – the yellow fat curve, is the offset (b. S) r f b. S by r • We further restrict all changes to the Mortar – the green region, is the mortar Mr(b. S)=(b. S r) r of S • We explain why in the next few slides Mortar Envelop NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 5

We need a vocabulary To discuss and to measure simplicity, we need precise terms • We will use three different measures – Smothness (value defined using Differential Geometry) – Regularity (value defined using Morphology) – Mortar (area near the details defined using Morphology) • We want to be able to: – – – Measure smoothness at every point of the boundary of the shape Measure regularity at every point in space Measure the global regularity and smoothness of the whole shape Define and compute the Mortar for the desired tolerance Simplify the shape in the Mortar: increasing its regularity & smoothness • A boundary point may be r-smooth or not, r-regular or not NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 6

r-smoothness • A shape S is r-smooth if the curvature of every point B in its boundary b. S exceeds r not r-smooth r: • How to check for r-smoothness at B? B – For C 2 curves: compare radius of curvature to r – For polygons: estimate radius of curvature A • R=v 2/(a v) z, where v=AC/2 and a=BC–AB C • A point may be r-smooth, but not r-regular NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 7

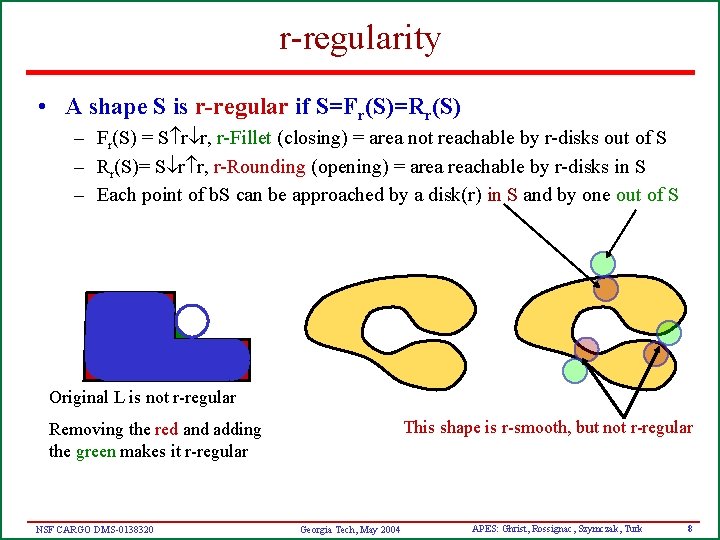
r-regularity • A shape S is r-regular if S=Fr(S)=Rr(S) – Fr(S) = S r r, r-Fillet (closing) = area not reachable by r-disks out of S – Rr(S)= S r r, r-Rounding (opening) = area reachable by r-disks in S – Each point of b. S can be approached by a disk(r) in S and by one out of S Original L is not r-regular This shape is r-smooth, but not r-regular Removing the red and adding the green makes it r-regular NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 8

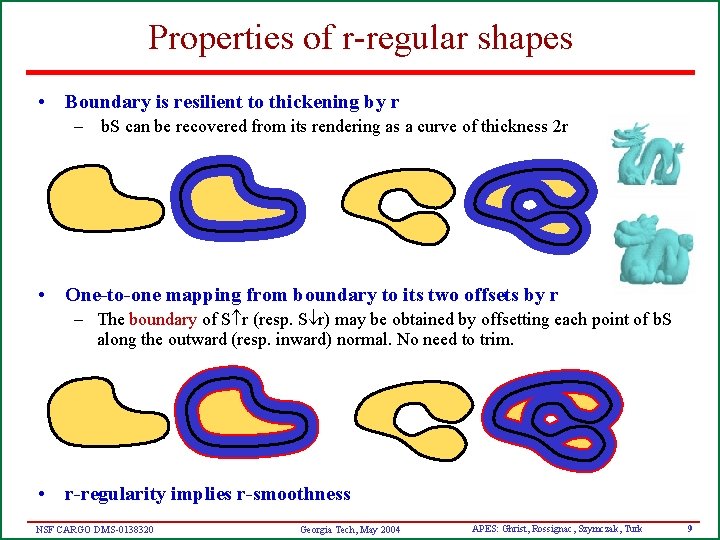
Properties of r-regular shapes • Boundary is resilient to thickening by r – b. S can be recovered from its rendering as a curve of thickness 2 r • One-to-one mapping from boundary to its two offsets by r – The boundary of S r (resp. S r) may be obtained by offsetting each point of b. S along the outward (resp. inward) normal. No need to trim. • r-regularity implies r-smoothness NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 9

When is a point of b. S smooth, regular? • How to check for r-regularity at B? – Check whether offset points is at distance r from b. S • Dist(B±r. N, b. S)<r ? – Want a set-theoretic definition? • B is r-regular if it does not lie in the mortar Mr(S) • The mortar is the set of all points that are not r-regular • It is defined in the next slide NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 10

Mortar (definition) Original set S Fillet: Fr(S) Adds the green Rounding: Rr(S) Removes the red Mortar: Mr(S) = Fr(S) – Rr(S) Core = Rr(S) Anticore = Fr(S) The plane is divided into core, mortar, and aniticore NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 11

Example of Mortar Core Original shape Mortar NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 12

Properties of the mortar • All points of the mortar are closer than r to the boundary b. S – Restricting the effect of simplification to the mortar will ensure that we do not modify the shape in places far from its boundary • The mortar excludes r-regular regions – Restricting the effect of simplification to the mortar will ensure that regular portions of the boundary are not affected by simplification S NSF CARGO DMS-0138320 Mr(S) Georgia Tech, May 2004 M 2 r(S) APES: Ghrist, Rossignac, Szymczak, Turk 13

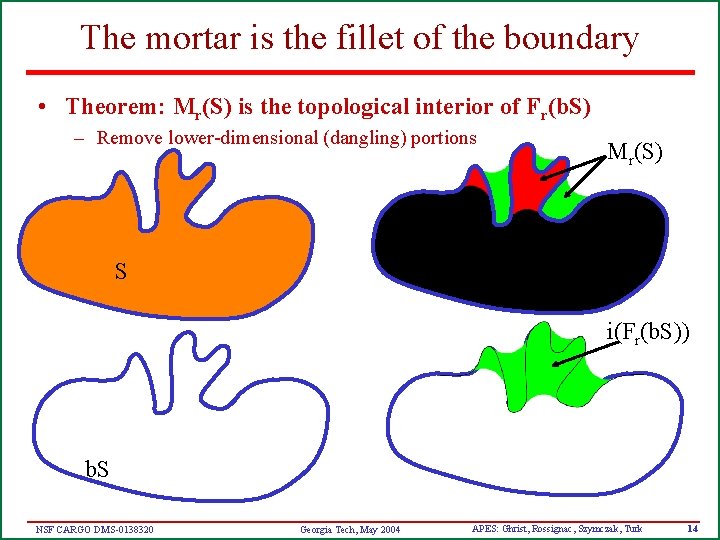
The mortar is the fillet of the boundary • Theorem: Mr(S) is the topological interior of Fr(b. S) – Remove lower-dimensional (dangling) portions Mr(S) S i(Fr(b. S)) b. S NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 14

Using the Mortar to decompose b. S Given r, the regular segments of S are defined as the connected components of r-regular points of b. S. • Th 1: Regular segment = connected component of b. S–Mr(S) • Places where the core and anticore touch • Th 2: Irregular segment = connected component of b. S Mr(S) • Note that irregular points may still be r-smooth Regular segments Mr(S) = Fr(S) – Rr(S) Core = Rr(S) NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 15

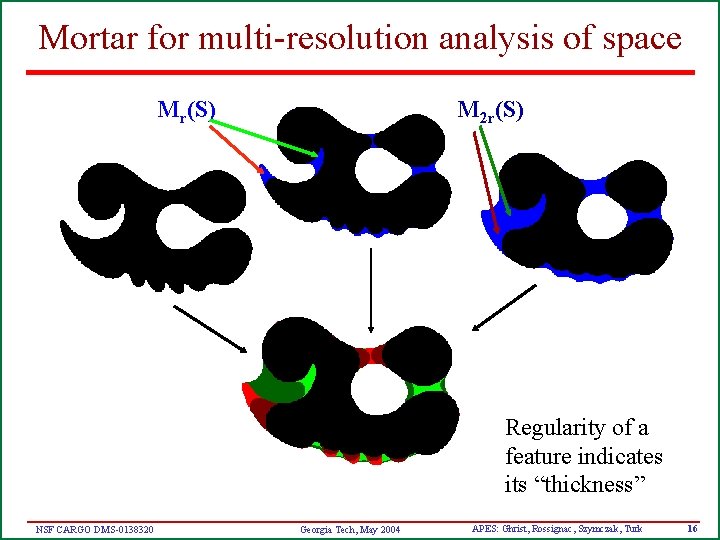
Mortar for multi-resolution analysis of space Mr(S) M 2 r(S) Regularity of a feature indicates its “thickness” NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 16

Analyzing the regularity of space • The regularity of a point B with respect to a set S is defined as the minimum r for which B Mr(S) – Points close to sharp features or constrictions are less regular – Different from signed distance field NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 17

Morphological Simplifications • Fillet (closing) fills in creases and concave corners • Rounding (opening) removes convex corners and branches • Fillet and rounding operations may be combined to produce more symmetric filters that tend to smoothen both concave and convex features • Fr(Rr(S)) and Rr(Fr(S)) combinations tend to: – – Simplify topology: Eliminate small holes and components Smoothen the shape almost everywhere Regularize almost everywhere Increase roundness (by reducing perimeter) • However they – Do not guarantee r-regularity or r-smoothness – Tend to increase or to decrease the density NSF CARGO DMS-0138320 Georgia Tech, May 2004 Neither Fr(Rr(S)) nor Rr(Fr(S)) will make this set r-regular APES: Ghrist, Rossignac, Szymczak, Turk 18

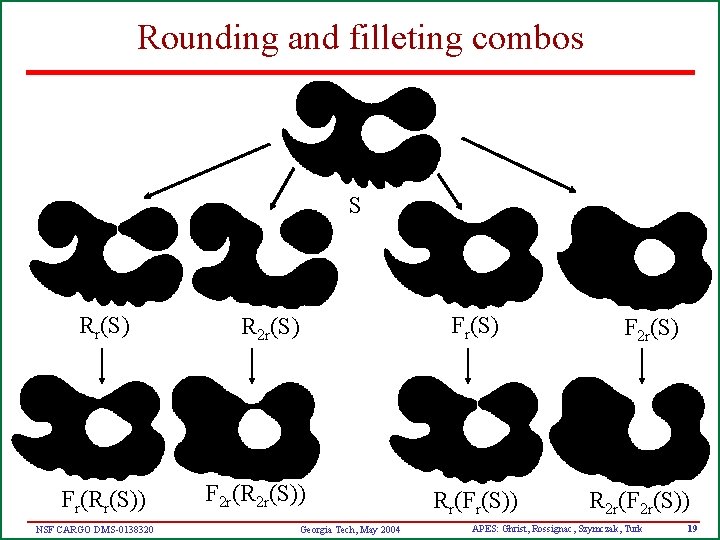
Rounding and filleting combos S Rr(S) Fr(Rr(S)) NSF CARGO DMS-0138320 Fr(S) R 2 r(S) F 2 r(R 2 r(S)) Georgia Tech, May 2004 Rr(Fr(S)) F 2 r(S) R 2 r(F 2 r(S)) APES: Ghrist, Rossignac, Szymczak, Turk 19

Which is better: FR or RF? Removed by rounding S Rr(S) Which option is better? Fr(S) The one that best preserves average density Fr(Rr(S)) NSF CARGO DMS-0138320 Rr(Fr(S)) Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 20

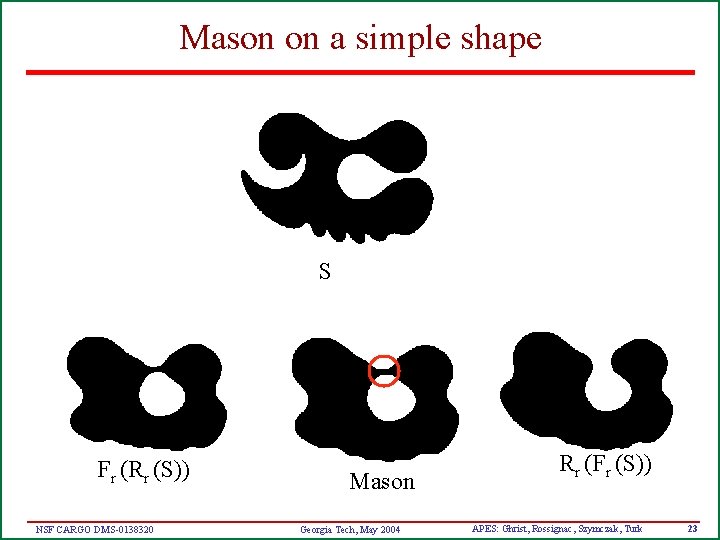
The Mason filter • We don’t have to make a global choice of FR versus RF • Do it independently for each component of the mortar • The Mason algorithm For each connected segment M of Mr(S) replace M S by M Fr(Rr(S)) or by M Rr(Fr(S)), whichever best preserves the shape i. e. , minimizes area of the symmetric difference between original and result “Mason: Morphological Simplification", J Williams, A Powell, and J Rossignac. GVU Tech. Report GIT-GVU-04 -05. http: //www. gvu. gatech. edu/~jarek/papers. html • Mason preserves density (average area) better than a global Fr(Rr(S)) or Rr(Fr(S)), but does not guarantee smoothness nor minimality of perimeter NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 21

Mason in Granada S Fr(Rr(S)) NSF CARGO DMS-0138320 Mortar Mr(S): removed&added Mason Georgia Tech, May 2004 Rr(Fr(S)) APES: Ghrist, Rossignac, Szymczak, Turk 22

Mason on a simple shape S Fr (Rr (S)) NSF CARGO DMS-0138320 Mason Georgia Tech, May 2004 Rr (Fr (S)) APES: Ghrist, Rossignac, Szymczak, Turk 23

3 D Mason in China NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 24

Can we improve on Mason? • Want to ensure r-smoothness • Want to minimize perimeter • Willing to give up some r-regularity • Willing to give up some density preservation • Formulate the solution using a Tight Hull… next slide NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 25

Tight Hulls • The tight hull, TH(R, F), of a set R inside a set F is the set H that has the smallest perimeter and satisfies R H F – Extends the idea of a convex hull, CH(R), which may be defined in 2 D as the simply connected set that contains R and has smallest perimeter. Hence, CH(R)=TH(R, F) where F is the whole plane. F R • b. H is the shortest path around R in F NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 26

Related prior art • O(n) algorithm exists based on the Visibility graph – “Euclidean shortest path in the presence of rectilinear barriers”, D. T. Lee and. P. Preparata, Netwirks, 14: 393 -410, 1984 – “Shortest paths and networks” Joe Mitchell, in Handbook of Discrete and Computational Geometry, Page 610, 2004. – “Shortest Paths in the Plane with Polygonal Obstacles" J Storer and J Reif • Relative convex hull – Jack Sklansky and Dennis F. Kibler. A theory of nonuniformly digitized binary pictures. IEEE Transactions on Systems, Man, and Cybernetics, SMC-6(9): 637647, 1976. – http: //www. cs. mcgill. ca/~stever/pattern/MPP/node 7. html#SECTION 0004100000000 • Minimal Perimeter Polygon – Steven M. Robbin, April 97 – http: //www. cs. mcgill. ca/~stever/pattern/MPP/talk. html NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 27

Properties of tight hulls • Let H= TH(R, F) • b. H contains the portions of b. R that are on the convex hull of R – b. R b. CH(R) b. H • b. H is made of some convex portions of b. R and of some concave portions of b. F joined by short-cuts (straight edges) • Edge (A, B) is a short-cut if A is a silhouette point for B and vice versa. F R NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 28

Computing tight hulls for polygons • Start with CH(R), the convex hull of R • Identify each edge (A, B) of CH(R) that is not on b. R and that crosses b. F • Compute shortest path from A to B in F–R NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 29

Computing tight hulls for smooth shapes • Shortest path – Reasonably easy for shapes bounded by lines and circular arcs. • Track minimum distance field backwards – Propagate constrained distance field from A – Walk back from B along the gradient until you reach A • Constrained curvature flow – Iterative smoothing (contraction) of boundary of Fr(S) while preventing penetration in Rr(S) and in the complement of Fr(S) • Morphological shaving (for discrete representations) – Grow core by adding to it straight line segments of contiguous mortar pixels that start and end at a core pixel NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 30

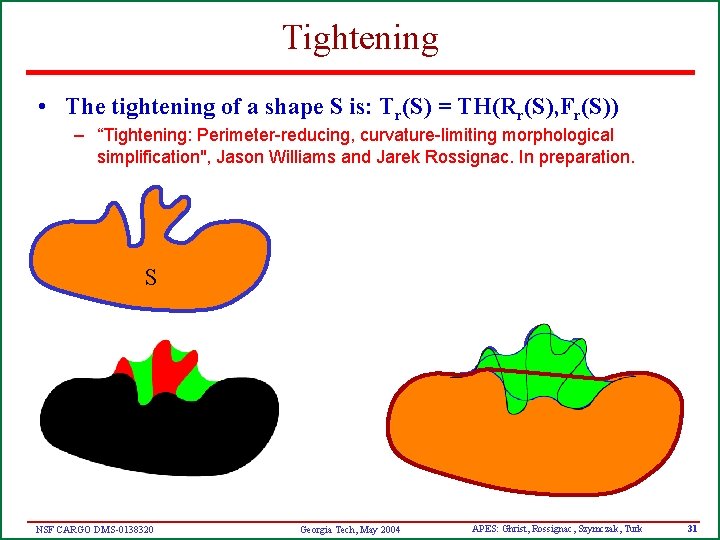
Tightening • The tightening of a shape S is: Tr(S) = TH(Rr(S), Fr(S)) – “Tightening: Perimeter-reducing, curvature-limiting morphological simplification", Jason Williams and Jarek Rossignac. In preparation. S NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 31

Example of tightening NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 32

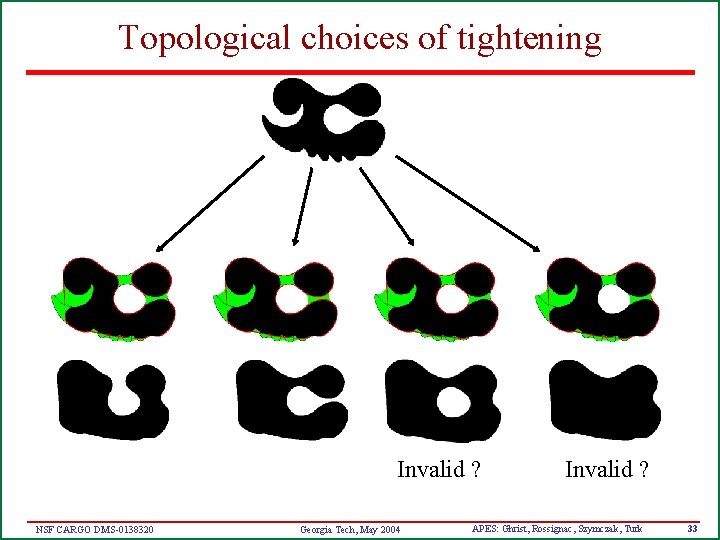
Topological choices of tightening Invalid ? NSF CARGO DMS-0138320 Georgia Tech, May 2004 Invalid ? APES: Ghrist, Rossignac, Szymczak, Turk 33

Properties of tightenings • b. Tr(S) is r-smooth • Tr(S) may have irregular parts NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 34

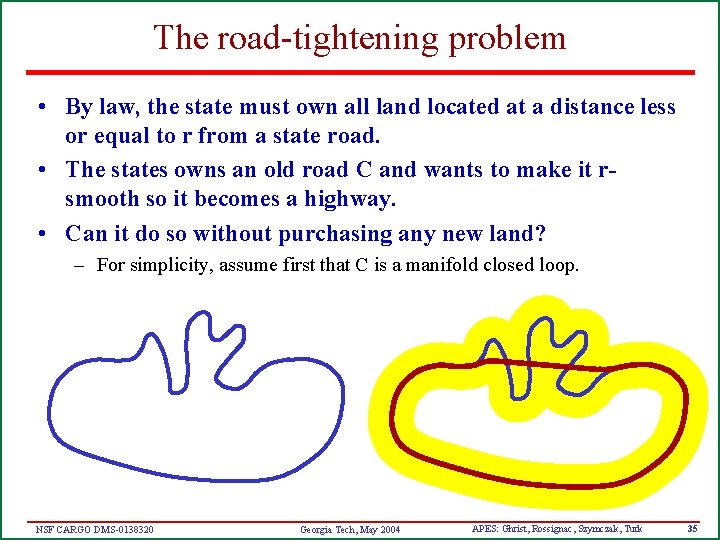
The road-tightening problem • By law, the state must own all land located at a distance less or equal to r from a state road. • The states owns an old road C and wants to make it rsmooth so it becomes a highway. • Can it do so without purchasing any new land? – For simplicity, assume first that C is a manifold closed loop. NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 35

3 D tightening NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 36

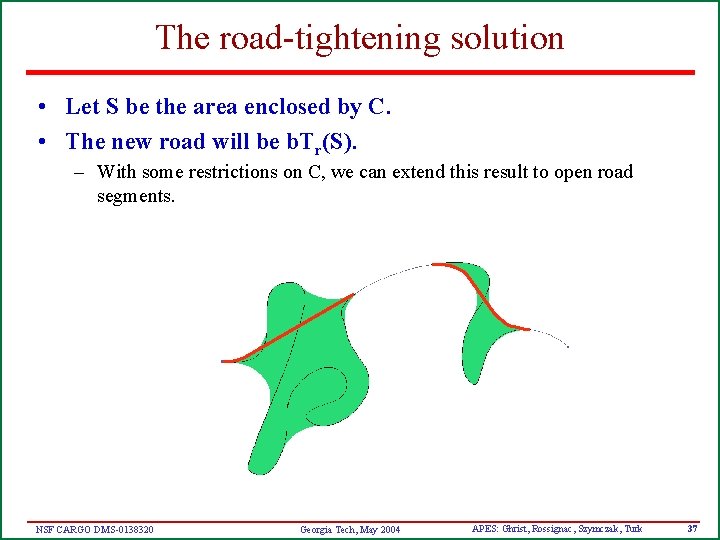
The road-tightening solution • Let S be the area enclosed by C. • The new road will be b. Tr(S). – With some restrictions on C, we can extend this result to open road segments. NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 37

Comparisons simplified shapes R(F(S)) tightening NSF CARGO DMS-0138320 F(R(S )) m as on Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 38

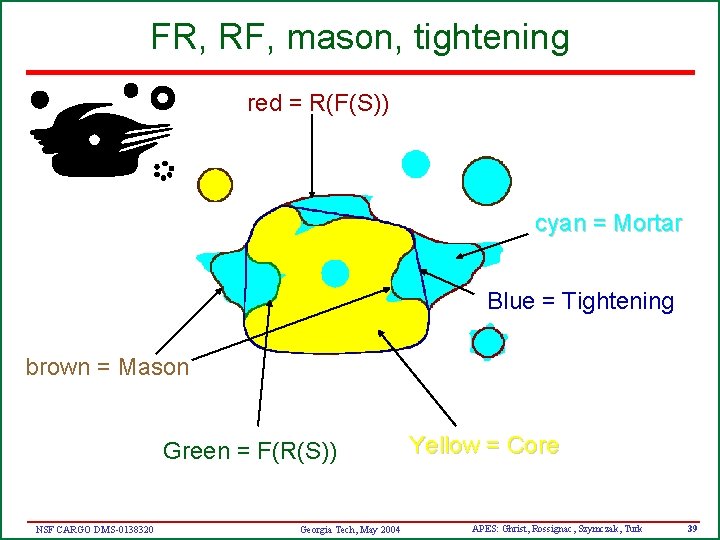
FR, RF, mason, tightening red = R(F(S)) cyan = Mortar Blue = Tightening brown = Mason Green = F(R(S)) NSF CARGO DMS-0138320 Georgia Tech, May 2004 Yellow = Core APES: Ghrist, Rossignac, Szymczak, Turk 39

Summary and future work • We propose to measure simplicity by regularity and smoothness – Defining regularity for all points of space will support a multi-resolution analysis of shape (interior, boundary, exterior) • We restrict simplifications to the mortar, ensuring that regular areas are preserved – Mason improves on FR and RF combos by better preserving density – Tightening improves on Mason by minimizing perimeter and guaranteeing r-smoothness – We have applied it to the tightening of curves • Future plans – Multi-resolution shape analysis and segmentation using regularity – Higher dimensions: surfaces, volumes, animations NSF CARGO DMS-0138320 Georgia Tech, May 2004 APES: Ghrist, Rossignac, Szymczak, Turk 40