The Solution of a Difference Equation for a

The Solution of a Difference Equation for a Compound Interest Account

Basic Compound Interest Formula Recall that the new balance of an account that earns compound interest can be found by using the formula Bnew = (1 + i) Bprevious. Recall the following: • Bnew represents the new balance (which can also be thought of as the next balance) • Bprevious represents the previous balance • i represents the interest rate per compound period (i. e. i = r/m)

Formula for a Future Balance of a Compound Interest Account A future balance of a compound interest account can be found by using the formula F = (1 + i)n. P. Recall the following: • F represents the future balance • n represents the number of compound periods • i represents the interest rate per compound period (i. e. i = r/m) • P represents the principal deposited into the account • The above formula allows us to find a future balance without having to find any of the previous balances.

The formula, F = (1 + i)n. P , is a solution of the difference equation Bnew = (1 + i) Bprevious. The following slides are a proof of the above statement.

Recall the General Form of a Difference Equation In chapter 11, a generalized difference equation (with an initial value) is written as: yn = a∙yn-1 + b , y 0 where • yn represents the next value in the list • yn-1 represents the previous value in the list • a is some value that is the coefficient of yn-1 • b is some constant value • y 0 is the initial value

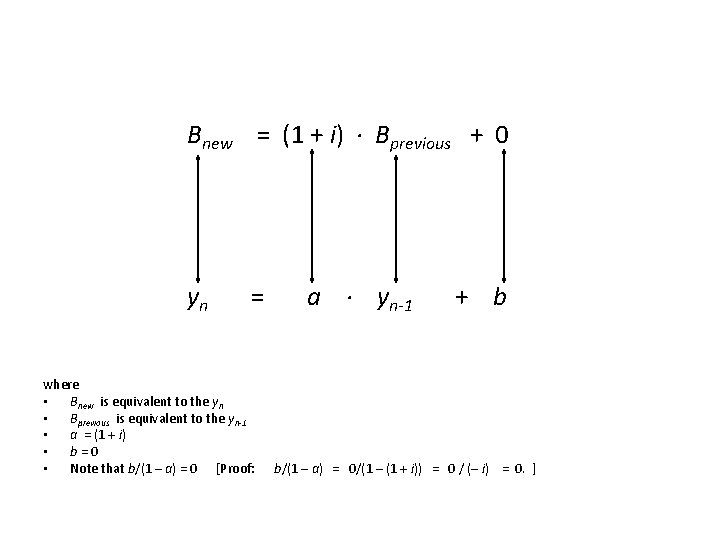
The formula Bnew = (1 + i)Bprevious is a difference equation since it is in the form of yn = a∙yn-1 + b. The next slide will show this, but first we will rewrite Bnew = (1 + i)Bprevious as Bnew = (1 + i)∙Bprevious + 0.

Bnew = (1 + i) ∙ Bprevious + 0 yn = where • Bnew is equivalent to the yn • Bprevious is equivalent to the yn-1 • a = (1 + i) • b=0 • Note that b/(1 – a) = 0 [Proof: a ∙ yn-1 + b b/(1 – a) = 0/(1 – (1 + i)) = 0 / (– i) = 0. ]

The Initial Value The initial value, y 0 , for a account that earns compound interest is the principal, P (which is the initial deposit). Thus y 0 = P.

Recall When Solving a Difference Equation Since a ≠ 1 (the reason will be, or was, discussed in the lecture), then the solution of the difference equation can be found using yn = b/(1 – a) + ( y 0 – b/(1 – a) ) an. Now substituting the chapter 10 notations into the above formula.

The Substitutions Substituting 0 for b/(1 – a), P for y 0 , and (1+i) for a, the solution of yn = b/(1 – a) + ( y 0 – b/(1 – a) ) an becomes yn = 0 + ( P – 0) (1+i)n. Note that we did not change the notation of yn ; we will address this later.

Simplification Using Algebra The formula yn = 0 + ( P – 0) (1+i)n can be simplified to yn= P (1 + i)n ; which is equivalent to yn= (1 + i)n P . We used the additive property of 0 and the commutative property of multiplication.

The yn Notation Change Now since yn , in yn= (1 + i)n P , represents a specified value in the list (mainly the nth value in the list after the initial value) without using any of the previous values (with the exception of the initial value P), the yn can be changed to an F to represent the future value. So yn= (1 + i)n P is changed to F = (1 + i)n P.

Therefore F = (1 + i)n P is the solution of the difference equation Bnew = (1 + i)Bprevious. Q. E. D.