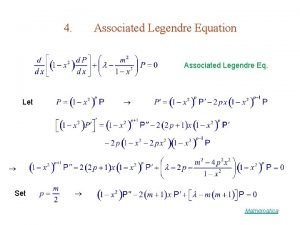1 3 Solution of Dynamical Equation 1 Solution





















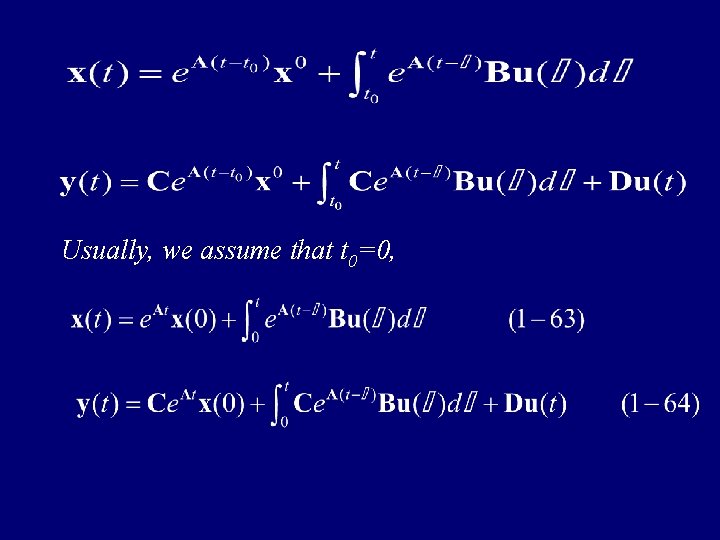




- Slides: 26

§ 1 -3 Solution of Dynamical Equation 1. Solution of homogeneous differential equation We first introduce a preliminary theorem for Preliminary Theorem Let every element of A and f be continuous over ( , + ). Then for any t 0 ( , + ) and any constant vector x 0, (A 1) has a solution x(t) defined over ( , + ), such that

Furthermore, the solution satisfying (A 2) is unique.

Corollary: If equation is a solution to the differential and for some t 0 , , then Proof It is clear that is one of the solutions of the above equation. And we also know that Since the solution with the initial condition is unique, we have Q. E. D

Theorem 1 -2 All solutions of dx/dt=A(t)x form an ndimensional vector space over the field of real numbers. We should prove that a) All the solutions form a linear space; b) The dimension of the space is n. More specifically, the proof includes 1) dx/dt=A(t)x has n linearly independent solutions; 2) Any solution can be expressed as the linear combination of the n solutions.

Proof a) All the solutions form a linear space Let 1 and 2 be two arbitrary solutions of dx/dt=A(t)x. Then for any real numbers 1 and 2, we have

b) The dimension of the space is n. 1) Let be n linearly independent vectors. is the solution of under the condition that (i=1,2,…,n) We then prove that independent over ( , + ). are linearly The proof is by contradiction. If there exists a t ( , + ), such that is linearly dependent then, there exists a n× 1

Nonzero vector , such that Note that (t) 0 t is a solution of dx/dt=A(t)x and is also a solution of dx/dt=A(t)x under the initial condition that The uniqueness of the solution implies that

In particular, for t=t 0 which means that the vectors are linearly dependent, which contradicts the hypothesis. Hence are linearly independent over .

2) To prove that any solution can be expressed as the linear combination of the n solutions. That is, all the solutions of dx/dt=A(t)x form an ndimensional vector space. Let be an arbitrary solution of dx/dt=A(t)x under the initial condition It is clear that e can be uniquely expressed as

It is easy to verify that is the solution of dx/dt=A(t)x under the initial condition The uniqueness of the solution implies that Q. E. D

2. Fundamental matrix and state transition matrix 1) Fundamental matrix Definition 1 -8: The matrix which is formed by the n linearly independent solutions of is said to be a fundamental matrix of. From Theorem 1 -2, the fundamental matrix has the following properties: where E is a nonsingular constant matrix.

Theorem 1 -3 The fundamental matrix of equation is nonsingular for every t over. Corollary Let be a solution of differential equation for some t 0, then we have . If

Theorem 1 -3 The fundamental matrix of equation is nonsingular for every t over. Proof The proof is by contradiction. Suppose the fundamental matrix is singular for some t 0. It follows that there exists a nonzero vector , such that which, together with the fact that is a solution of , implies that This contradicts the assumption. Q. E. D

Theorem 1 -4 Let and be the fundamental matrixes of dx/dt=A(t)x. Then there exists a n×n nonsingular constant matrix C, such that

2) State transition matrix Definition 1 -9 Let be any fundamental matrix. Then is said to be the state transition matrix of (1 -50). where 3) From the definition we immediately have the following important properties of the state transition matrix:

4). Properties of fundamental matrix It is easy to prove that is the unique solution of the following differential matrix equation 5). Under the condition dx/dt=A(t)x is , the solution of (1-53) Hence, can be considered as a linear transformation which maps the state at t 0 to the

state x(t) at time t. In fact, x(t) can always be expressed as In particular, from which we can obtain the conclusion. Example: Prove that the state transition matrix is unique, i. e. the state transition matrix is regardless of the choice of fundamental matrix.

3. Non-homogeneous equation 1) Solutions of linear time-variant dynamical equations Let

Theorem 1 -5 The solution of the state equation is given by where is called zero-input response, and is called zero-state response.

2) Relationship between I/O and state space descriptions Corollary 1 -5 The output of the dynamical equation (134) is If x(t 0)=0, the impulse response matrix is

3) Solutions of linear time-invariant dynamical equations Consider the following linear time-invariant dynamical equation where A, B, C and D are n×n, n×p, q×n and q×p real constant matrices. From the corresponding homogeneous equation, we have Fundamental matrix: State transition matrix:
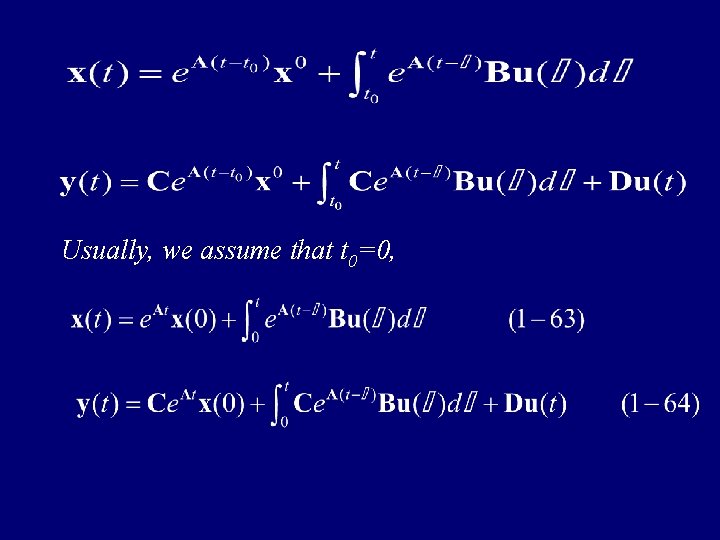
Usually, we assume that t 0=0,

The corresponding impulse response matrix is Usually we write it as The corresponding transfer function matrix of the above equation is which is a rational function matrix.

4. Equivalent transformation and equivalent dynamical equations 1. Equivalent dynamical of time-invariant system Definition 1 -10 Linear time-invariant equation is said to be a equivalent equations of (A, B, C, D) if and only if there exists a nonsingular matrix P, such that (1 — 68)

Definition (zero-state equivalence) Two timeinvariant dynamical systems are said to be zero-state equivalent if and only if they have the same impulse response matrix or the same transfer function matrix.

Example: Consider the two systems which are not equivalent dynamical equations, but are zero-state equivalent.
 Dynamical systems neuroscience
Dynamical systems neuroscience Dynamical systems theory motor development
Dynamical systems theory motor development Tdb urban dictionary
Tdb urban dictionary Accelarationist
Accelarationist Dynamical mean-field theory
Dynamical mean-field theory Dynamical
Dynamical Automata
Automata Siam conference on applications of dynamical systems
Siam conference on applications of dynamical systems Immiscible
Immiscible Spherical wave equation
Spherical wave equation Solution set of linear equation
Solution set of linear equation Factor quadratic equations
Factor quadratic equations Equation
Equation General solution of partial differential equation
General solution of partial differential equation An example of a quadratic function
An example of a quadratic function Integrating factor method
Integrating factor method Find the general solution of the differential equation
Find the general solution of the differential equation Which is the quadratic term
Which is the quadratic term Find the solution
Find the solution What is a first order equation
What is a first order equation Which ordered pair is a solution of the equation
Which ordered pair is a solution of the equation General solutions of differential equations
General solutions of differential equations Analytical solution of first order differential equation
Analytical solution of first order differential equation Solution of bessel differential equation
Solution of bessel differential equation How do you balance a chemical equation
How do you balance a chemical equation Logistic differential equation solution
Logistic differential equation solution Associated legendre polynomials mathematica
Associated legendre polynomials mathematica