low LOD 70000 triangles Simplification Jarek Rossignac GVU










- Slides: 12

low LOD 70000 triangles Simplification Jarek Rossignac GVU Center Georgia Institute of Technology Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 1

Loss-less or lossy compression? • Loss-less compression – Quantize parameters (coordinates) based on application needs • Finite precision measurements, design, computation • Limited needs for accuracy in some applications – Encode quantized location and exact incidence Quantize vertices Compress Lossy Binary format Decompress Loss-less • Lossy compression – Encode approximations of the surface using a different representation – How to measure the error to ensure that tolerance is not exceeded? Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 2

Triangle count reduction techniques (LOD) • Quantize & cluster vertex data (Rossignac&Borrel’ 92) – remove degenerate triangles (that have coincident vertices) – Adapted by P. Lindstrom for out-of-core simplification • Repeatedly collapse best edge (Ronfard&Rossignac 96) – while minimizing maximum error bound – Adapted by M. Garland for least square error Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 3

Vertex clustering (Rossignac-Borrel) • Subdivide box around object into grid of cells • Coalesce vertices in each cell into one “attractor” • Remove degenerate triangles – More than one vertex in a cell – Not needed for dangling edge or vertex Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 4

Rossignac&Borrel 93 Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 5

Rossignac&Borrel 93 Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 6

Improving on Vertex Clustering • Advantages – – – Trivial to implement Fast Works on any mesh or triangle soup Guaranteed Hausdroff error to diagonal of cell Reduces topology • Removes holes. Never creates one • Merges connected shells components. Never splits them. • Drawbacks – Produces sub-optimal results • Too much error for a given triangle count reduction – Prevents the merging of distant vertices on flat portions of the surface • Fix: limit vertex moves by the resulting error – Not a fixed grid Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 7

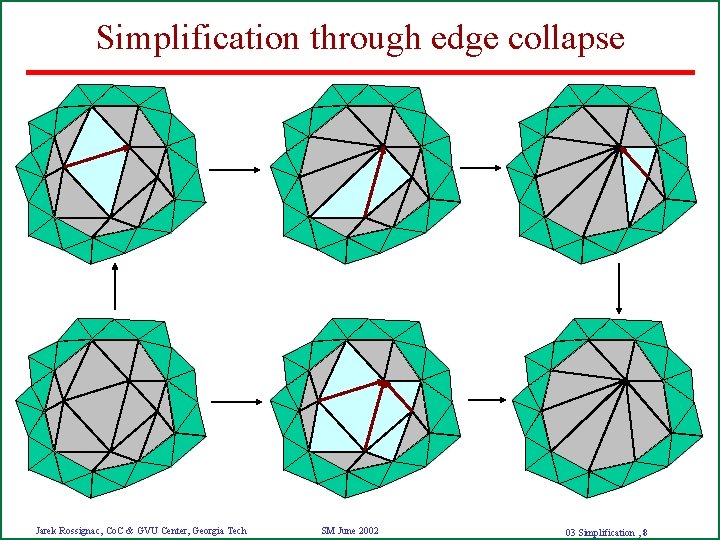
Simplification through edge collapse Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 8

How to decide which edges to collapse? • Minimize the error between original and resulting LOD – How to compute/estimate error – Peformance • Geometric proximity clustering of vertices (pessimistic) – Rossignac&Borrel: quantizing vertices identifies candidate edges – Error is bounded by the quantization error – Fast, easy, robust, but sub-optimal results • Collapse edges – Longer edges in almost planar regions – Estimate error as max distance to supporting planes (Ronfard&Rossignac) • Must keep list of all planes supporting triangles incident on contracted edges – Use sum of squares instead of max (Heckbert&Garland): faster, no bound • L 2 norm, needs only add 4 x 4 matrices when clusters are merged Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 9

Distance and quadratic error • Point-plane distance – – P N Point P=(x, y, z) Q Plane containing point Qm and having unit normal Nm Distance ||PQm Nm|| Can compute max (conservative, Ronfard&Rossignac) or sum (cheap, Heckbert&Garland) of (PQm Nm)2 for the planes of all the triangles Tm incident upon vertices merged at P • Distance squared: (PQm Nm)2 = amx 2+bmy 2+cmz 2+dmxy+emyz+fmzx+gmx+hmy+imz+jm • Sum of distances squared: (PQm Nm)2 + (PQn Nn)2 = (am+an)x 2 +(bm+bn)y 2 +(cm+cn)z 2 +(dm+dn)x +(em+en)y +(fm+fn)z +gm +gn P – As vertices are merged recursively: • With max, you need to remember all the planes Q • With sum, you just add the coefficients Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 10

Ronfard&Rossignac EG’ 96 Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 11

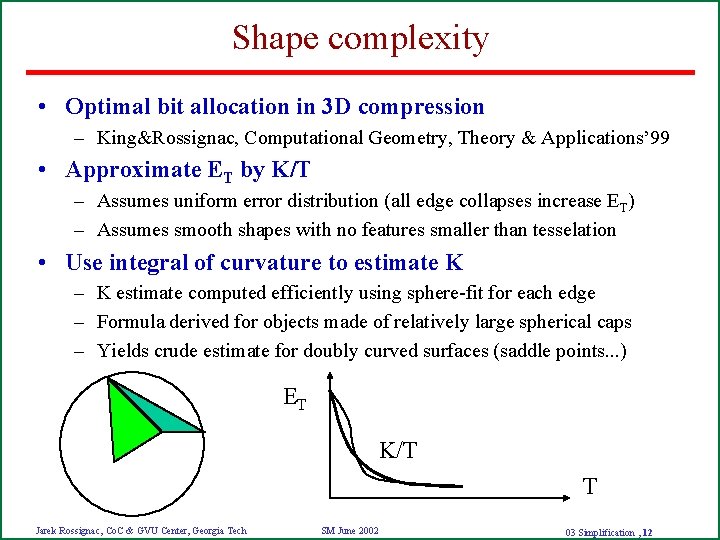
Shape complexity • Optimal bit allocation in 3 D compression – King&Rossignac, Computational Geometry, Theory & Applications’ 99 • Approximate ET by K/T – Assumes uniform error distribution (all edge collapses increase ET) – Assumes smooth shapes with no features smaller than tesselation • Use integral of curvature to estimate K – K estimate computed efficiently using sphere-fit for each edge – Formula derived for objects made of relatively large spherical caps – Yields crude estimate for doubly curved surfaces (saddle points. . . ) ET K/T T Jarek Rossignac, Co. C & GVU Center, Georgia Tech SM June 2002 03 Simplification , 12