SIMPLIFICATION OF FORCE AND COUPLE SYSTEMS FURTHER SIMPLIFICATION

SIMPLIFICATION OF FORCE AND COUPLE SYSTEMS & FURTHER SIMPLIFICATION OF A FORCE AND COUPLE SYSTEM Objectives: a) Determine the effect of moving a force. b) Find an equivalent force-couple system for a system of forces and couples.

APPLICATIONS What are the resultant effects on the person’s hand when the force is applied in these four different ways? Why is understanding these difference important when designing various load-bearing structures?

APPLICATIONS (continued) Several forces and a couple moment are acting on this vertical section of an I-beam. | | ? ? For the process of designing the Ibeam, it would be very helpful if you could replace the various forces and moment just one force and one couple moment at point O with the same external effect? How will you do that?

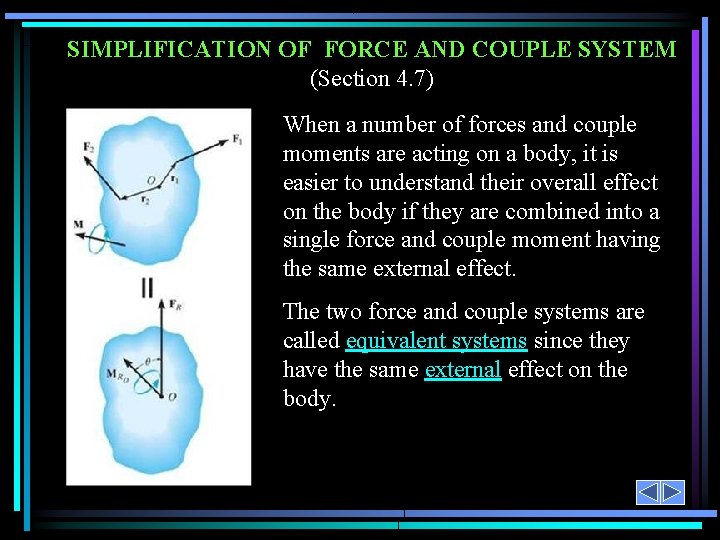
SIMPLIFICATION OF FORCE AND COUPLE SYSTEM (Section 4. 7) When a number of forces and couple moments are acting on a body, it is easier to understand their overall effect on the body if they are combined into a single force and couple moment having the same external effect. The two force and couple systems are called equivalent systems since they have the same external effect on the body.

MOVING A FORCE ON ITS LINE OF ACTION Moving a force from A to B, when both points are on the vector’s line of action, does not change the external effect. Hence, a force vector is called a sliding vector. (But the internal effect of the force on the body does depend on where the force is applied).

MOVING A FORCE OFF OF ITS LINE OF ACTION B When a force is moved, but not along its line of action, there is a change in its external effect! Essentially, moving a force from point A to B (as shown above) requires creating an additional couple moment. So moving a force means you have to “add” a new couple. Since this new couple moment is a “free” vector, it can be applied at any point on the body.

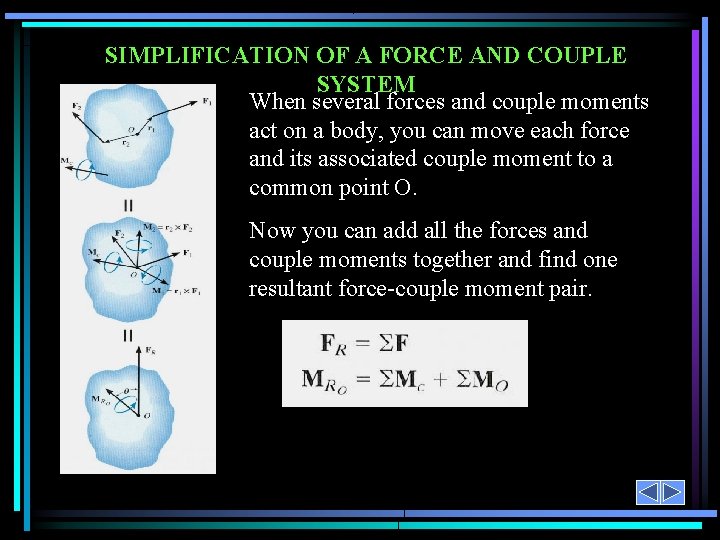
SIMPLIFICATION OF A FORCE AND COUPLE SYSTEM When several forces and couple moments act on a body, you can move each force and its associated couple moment to a common point O. Now you can add all the forces and couple moments together and find one resultant force-couple moment pair.

SIMPLIFICATION OF A FORCE AND COUPLE SYSTEM (continued) WR = W 1 + W 2 (MR)o = W 1 d 1 + W 2 d 2 If the force system lies in the x-y plane (a 2 -D case), then the reduced equivalent system can be obtained using the following three scalar equations.

FURTHER SIMPLIFICATION OF A FORCE AND COUPLE SYSTEM (Section 4. 8) = = If FR and MRO are perpendicular to each other, then the system can be further reduced to a single force, FR , by simply moving FR from O to P. In three special cases, concurrent, coplanar, and parallel systems of forces, the system can always be reduced to a single force.

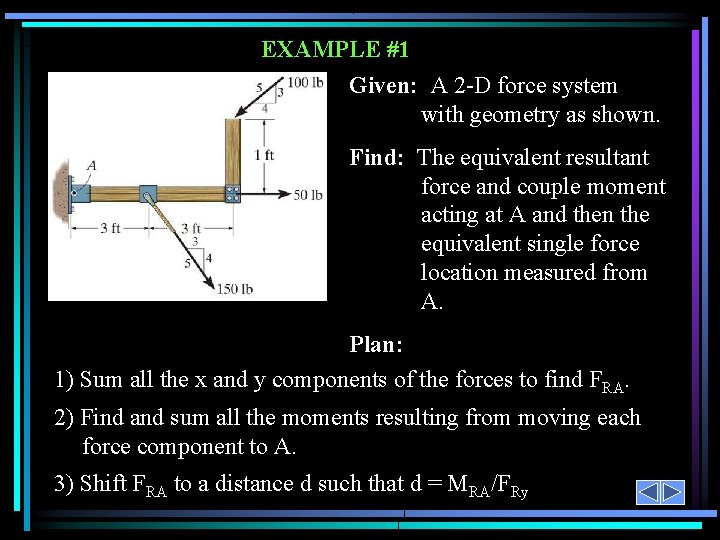
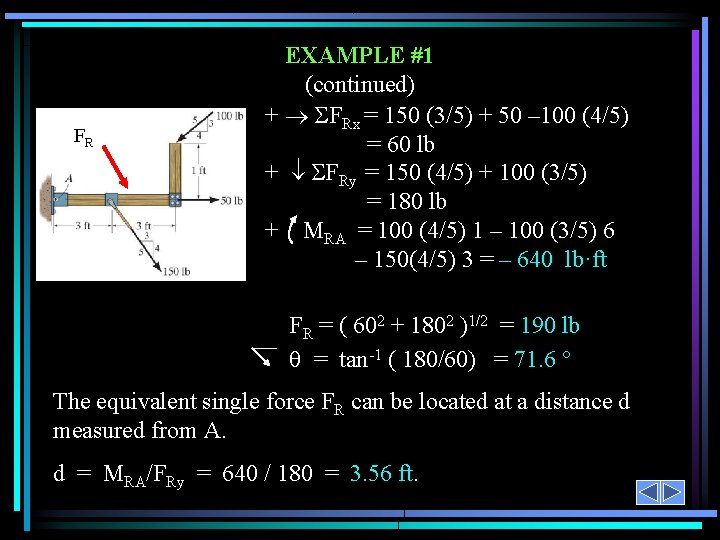
EXAMPLE #1 Given: A 2 -D force system with geometry as shown. Find: The equivalent resultant force and couple moment acting at A and then the equivalent single force location measured from A. Plan: 1) Sum all the x and y components of the forces to find FRA. 2) Find and sum all the moments resulting from moving each force component to A. 3) Shift FRA to a distance d such that d = MRA/FRy

FR EXAMPLE #1 (continued) + FRx = 150 (3/5) + 50 – 100 (4/5) = 60 lb + FRy = 150 (4/5) + 100 (3/5) = 180 lb + MRA = 100 (4/5) 1 – 100 (3/5) 6 – 150(4/5) 3 = – 640 lb·ft FR = ( 602 + 1802 )1/2 = 190 lb = tan-1 ( 180/60) = 71. 6 ° The equivalent single force FR can be located at a distance d measured from A. d = MRA/FRy = 640 / 180 = 3. 56 ft.

EXAMPLE #2 Given: The slab is subjected to three parallel forces. Find: Plan: The equivalent resultant force and couple moment at the origin O. Also find the location (x, y) of the single equivalent resultant force. 1) Find FRO = Fi = FRzo k 2) Find MRO = (ri Fi) = MRx. O i + MRy. O j 3) The location of the single equivalent resultant force is given as x = – MRy. O/FRz. O and y = MRx. O/FRz. O

EXAMPLE #2 (continued) FRO = {100 k – 500 k – 400 k} = – 800 k N MRO = (3 i) (100 k) + (4 i + 4 j) (-500 k) + (4 j) (-400 k) = {– 300 j + 2000 j – 2000 i – 1600 i} = { – 3600 i + 1700 j }N·m The location of the single equivalent resultant force is given as, x = – MRyo / FRzo = (– 1700) / (– 800) = 2. 13 m y = MRxo / FRzo = (– 3600) / (– 800) = 4. 5 m

GROUP PROBLEM SOLVING Given: A 2 -D force and couple system as shown. Find: The equivalent resultant force and couple moment acting at A. Plan: 1) Sum all the x and y components of the two forces to find FRA. 2) Find and sum all the moments resulting from moving each force to A and add them to the 45 k. N m free moment to find the resultant MRA.

GROUP PROBLEM SOLVING (continued) Summing the force components: + Fx = (5/13) 26 – 30 sin 30° = – 5 k. N + Fy = – (12/13) 26 – 30 cos 30° = – 49. 98 k. N Now find the magnitude and direction of the resultant. FRA = ( 5 2 + 49. 98 2 )1/2 = 50. 2 k. N and = tan-1 (49. 98/5) = 84. 3 ° + MRA = {30 sin 30° (0. 3 m) – 30 cos 30° (2 m) – (5/13) 26 (0. 3 m) – (12/13) 26 (6 m) – 45 } = – 239 k. N m

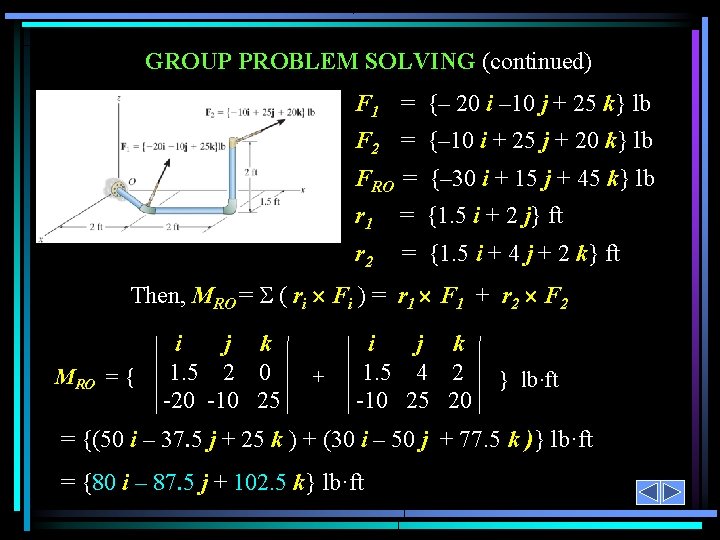
GROUP PROBLEM SOLVING (continued) Given: Forces F 1 and F 2 are applied to the pipe. Find: An equivalent resultant force and couple moment at point O. Plan: a) Find FRO = Fi = F 1 + F 2 b) Find MRO = MC + ( ri Fi ) where, MC are any free couple moments (none in this example). ri are the position vectors from the point O to any point on the line of action of Fi.

GROUP PROBLEM SOLVING (continued) F 1 = {– 20 i – 10 j + 25 k} lb F 2 = {– 10 i + 25 j + 20 k} lb FRO = {– 30 i + 15 j + 45 k} lb r 1 = {1. 5 i + 2 j} ft r 2 = {1. 5 i + 4 j + 2 k} ft Then, MRO = ( ri Fi ) = r 1 F 1 + r 2 F 2 MRO = { i j k 1. 5 2 0 -20 -10 25 + i j k 1. 5 4 2 -10 25 20 } lb·ft = {(50 i – 37. 5 j + 25 k ) + (30 i – 50 j + 77. 5 k )} lb·ft = {80 i – 87. 5 j + 102. 5 k} lb·ft

REDUCTION OF A SIMPLE DISTRIBUTED LOADING Objective: Determine an equivalent force for a distributed load. =

APPLICATIONS There is a bundle (called a bunk) of 2” x 4” boards stored on a storage rack. This lumber places a distributed load (due to the weight of the wood) on the beams holding the bunk. To analyze the load’s effect on the steel beams, it is often helpful to reduce this distributed load to a single force. How would you do this?

APPLICATIONS (continued) The uniform wind pressure is acting on a triangular sign (shown in light brown). To be able to design the joint between the sign and the sign post, we need to determine a single equivalent resultant force and its location.

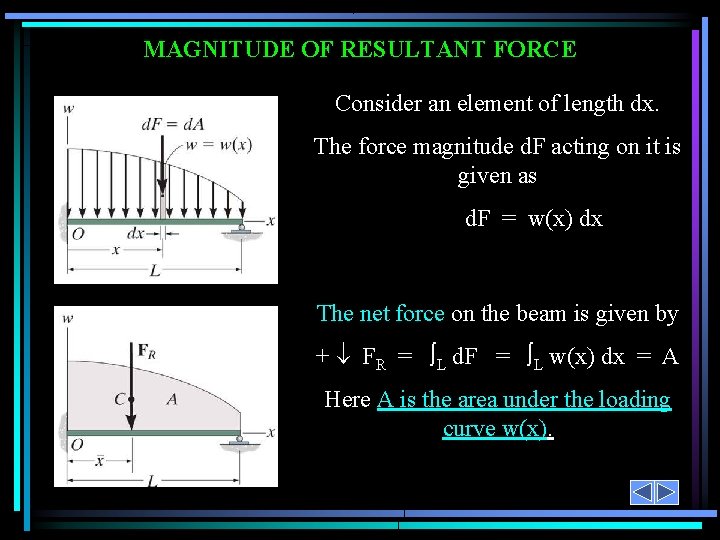
DISTRIBUTED LOADING In many situations, a surface area of a body is subjected to a distributed load. Such forces are caused by winds, fluids, or the weight of items on the body’s surface. We will analyze the most common case of a distributed pressure loading. This is a uniform load along one axis of a flat rectangular body. In such cases, w is a function of x and has units of force per length.

MAGNITUDE OF RESULTANT FORCE Consider an element of length dx. The force magnitude d. F acting on it is given as d. F = w(x) dx The net force on the beam is given by + FR = L d. F = L w(x) dx = A Here A is the area under the loading curve w(x).

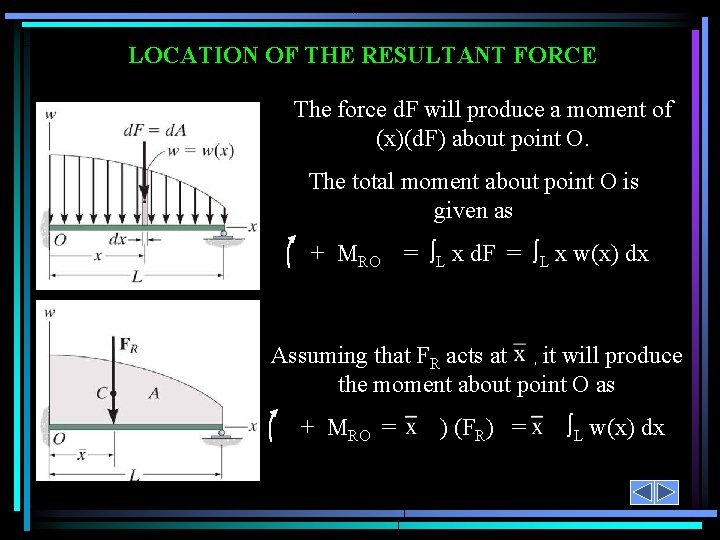
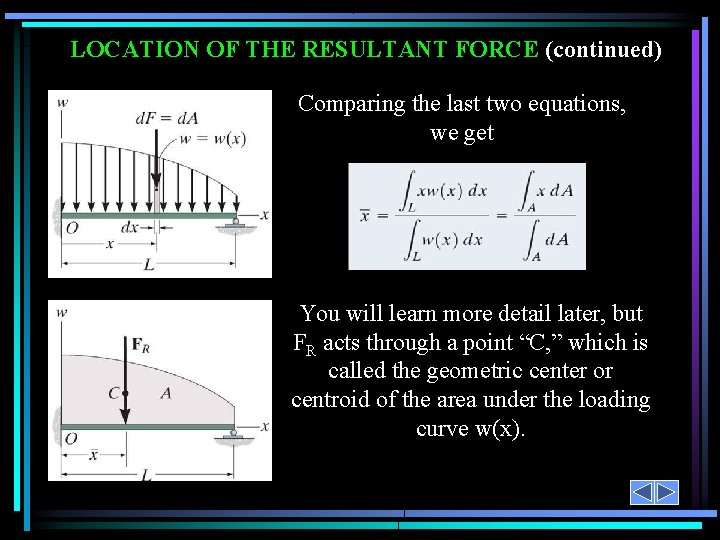
LOCATION OF THE RESULTANT FORCE The force d. F will produce a moment of (x)(d. F) about point O. The total moment about point O is given as + MRO = L x d. F = L x w(x) dx Assuming that FR acts at , it will produce the moment about point O as + MRO = ( ) (FR) = L w(x) dx

LOCATION OF THE RESULTANT FORCE (continued) Comparing the last two equations, we get You will learn more detail later, but FR acts through a point “C, ” which is called the geometric center or centroid of the area under the loading curve w(x).

EXAMPLES Until you learn more about centroids, we will consider only rectangular and triangular loading diagrams whose centroids are well defined and shown on the inside back cover of your textbook. Look at the inside back cover of your textbook. You should find the rectangle and triangle cases. Finding the area of a rectangle and its centroid is easy! Note that triangle presents a bit of a challenge but still is pretty straightforward.

EXAMPLES Now lets complete the calculations to find the concentrated loads (which is a common name for the resultant of the distributed load). The rectangular load: FR = 400 10 = 4, 000 lb andx = 5 ft. The triangular loading: FR = (0. 5) (600) (6) = 1, 800 N and x = 6 – (1/3) 6 = 4 m. Please note that the centroid in a right triangle is at a distance one third the width of the triangle as measured from its base.

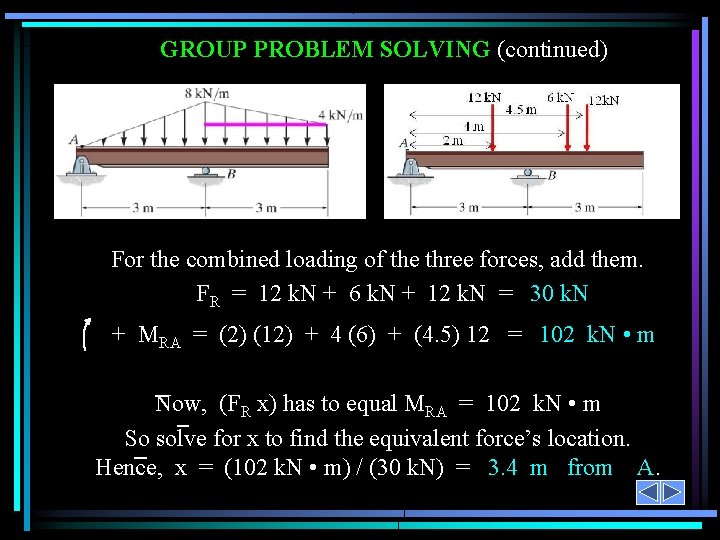
GROUP PROBLEM SOLVING Given: The loading on the beam as shown. Find: The equivalent force and its location from point A. Plan: 1) The distributed loading can be divided into three parts. (one rectangular loading and two triangular loadings). 2) Find FR and its location for each of these three distributed loads. 3) Determine the overall FR of the three point loadings and its location.

GROUP PROBLEM SOLVING (continued) For the left triangular loading of height 8 k. N/m and width 3 m, FR 1 = (0. 5) 8 k. N/m 3 m = 12 k. N x 1 = (2/3)(3 m) = 2 m from A For the top right triangular loading of height 4 k. N/m and width 3 m, FR 2 = (0. 5) (4 k. N/m) (3 m) = 6 k. N x 2 and its line of action is at = (1/3)(3 m) + 3 = 4 m from A For the rectangular loading of height 4 k. N/m and width 3 m, FR 3 = (4 k. N/m) (3 m) = 12 k. N and its line of action is atx 3 = (1/2)(3 m) + 3 = 4. 5 m from A

GROUP PROBLEM SOLVING (continued) For the combined loading of the three forces, add them. FR = 12 k. N + 6 k. N + 12 k. N = 30 k. N + MRA = (2) (12) + 4 (6) + (4. 5) 12 = 102 k. N • m Now, (FR x) has to equal MRA = 102 k. N • m So solve for x to find the equivalent force’s location. Hence, x = (102 k. N • m) / (30 k. N) = 3. 4 m from A.