MECH 401 Mechanical Design Applications Dr M Spring

MECH 401 Mechanical Design Applications Dr. M. Spring K. O’Malley 2008 – Master Notes Dr. D. M. Mc. Stravick Rice University

Failure from static loading n Topics q Failures from static loading n Ductile Failures q q n Brittle Failures q q q n Maximum Shear Stress Maximum Distortion Energy Maximum Normal Stress Coulomb-Mohr Modified Mohr Reading --- Chapter 5

What is Failure? n n Failure – any change in a machine part which makes it unable to perform its intended function. (From Spotts M. F. and Shoup T. E. ) We will normally use a yield failure criteria for ductile materials. The ductile failure theories presented are based on yield.

Failure Theories n Static failure q q q n Ductile Brittle Stress concentration Recall q Ductile n q Significant plastic deformation between yield and fracture Brittle n Yield ~= fracture

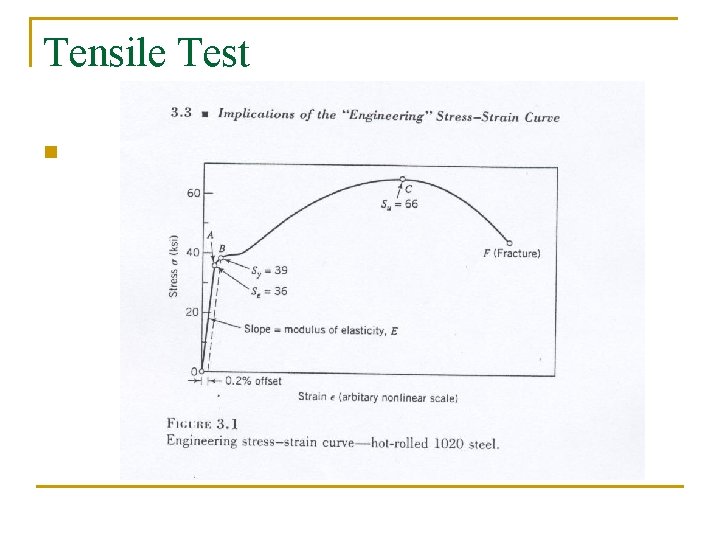
Tensile Test n

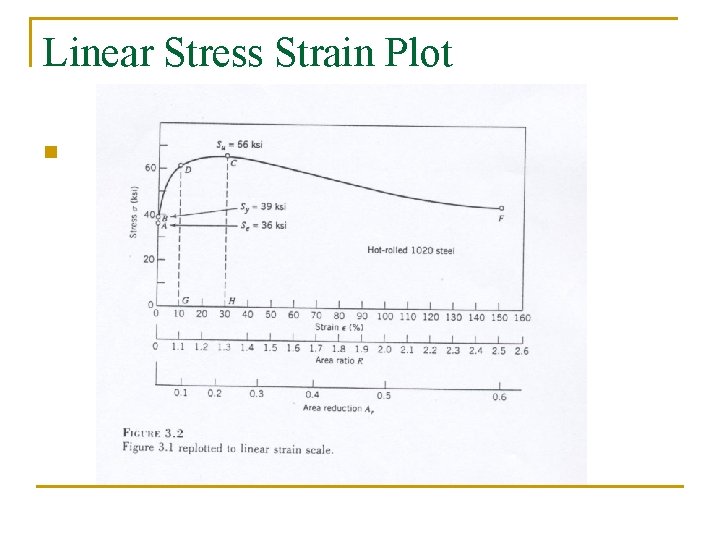
Linear Stress Strain Plot n

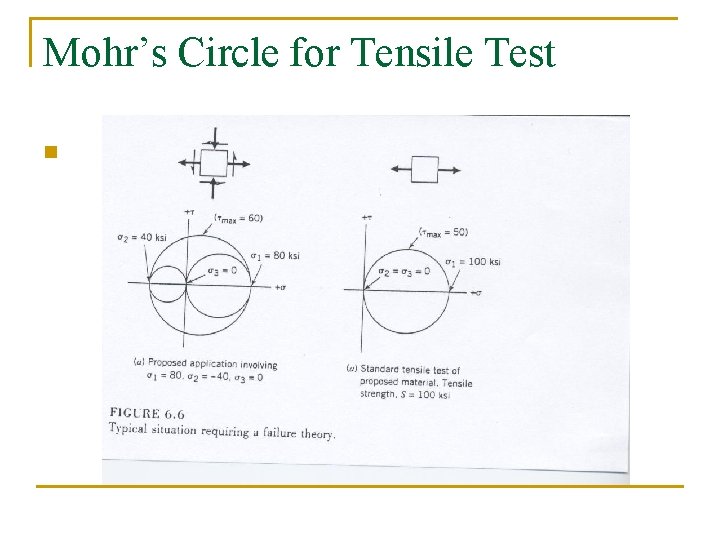
Mohr’s Circle for Tensile Test n

Static Ductile Failure n Two primary theories for static ductile failure q Von Mises criterion n n q Maximum Distortion-energy Theory MDE Maximum Shear Stress criterion n MSS

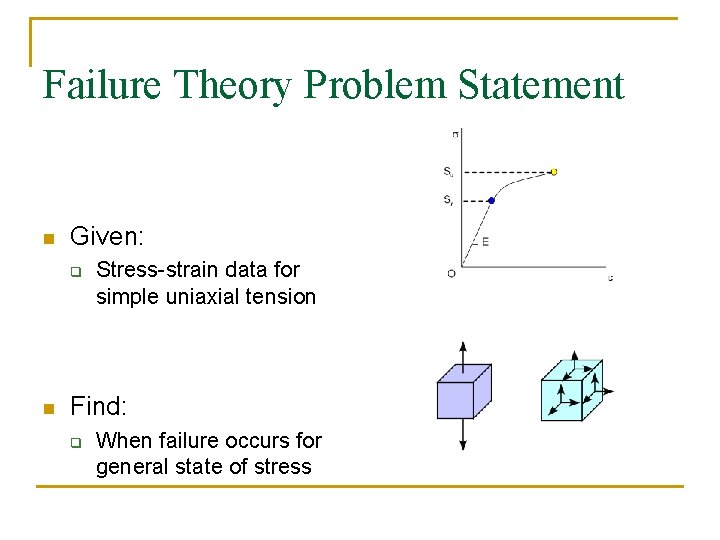
Failure Theory Problem Statement n Given: q n Stress-strain data for simple uniaxial tension Find: q When failure occurs for general state of stress

Static Ductile Failure n Max Shear Stress criterion q Material yields (fails) when: 1) 2) q Factor of Safety: or

Maximum Shear Stress Criteria n

Static Ductile Failure n Von Mises criterion q Let the Mises stress (se, equivalent stress) be: q Then failure (yield) occurs when: q Factor of Safety: n n Typically, Want a margin of error but not completely overdesigned

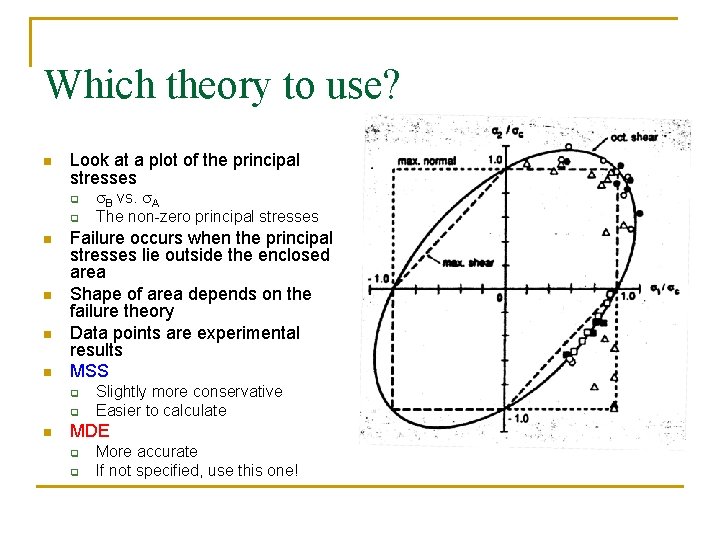
Which theory to use? n Look at a plot of the principal stresses q q n n Failure occurs when the principal stresses lie outside the enclosed area Shape of area depends on the failure theory Data points are experimental results MSS q q n s. B vs. s. A The non-zero principal stresses Slightly more conservative Easier to calculate MDE q q More accurate If not specified, use this one!

Comparison of MDE, MSS, MNS n

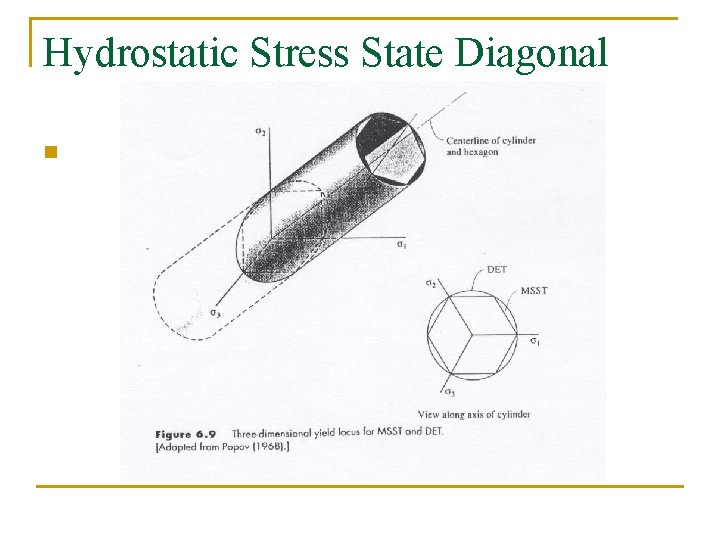
Hydrostatic Stress State Diagonal n

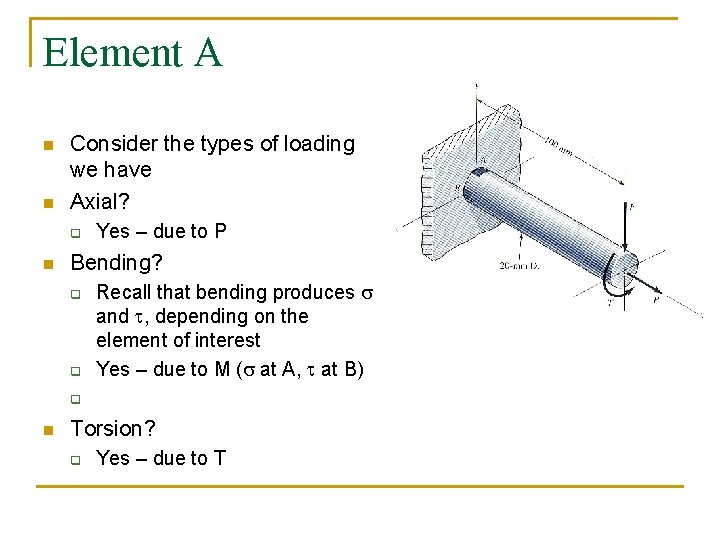
Ductile failure theory example n Given: q Bar is AISI 1020 hot-rolled steel n q q q n F = 0. 55 k. N P = 8. 0 k. N T = 30 Nm Find: q n A DUCTILE material Factor of safety ( ) Two areas of interest: q A n q Top – where max normal stress is seen (bending!) B n Side – where max shear stress is seen

Element A n n Consider the types of loading we have Axial? q n Yes – due to P Bending? q q Recall that bending produces s and t, depending on the element of interest Yes – due to M (s at A, t at B) q n Torsion? q Yes – due to T

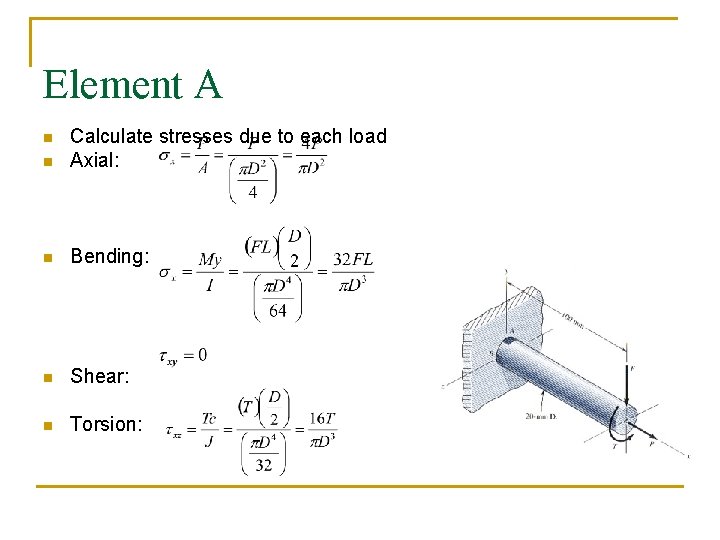
Element A n Calculate stresses due to each load Axial: n Bending: n Shear: n Torsion: n

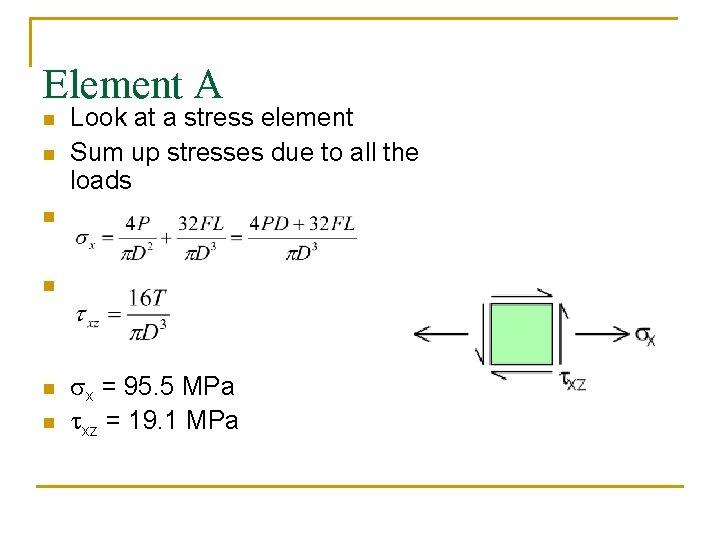
Element A n n Look at a stress element Sum up stresses due to all the loads n n sx = 95. 5 MPa txz = 19. 1 MPa

Element A Draw Mohr’s Circle with the n stresses that we calculated q q q sx = 95. 5 MPa txz = 19. 1 MPa x at (sx, txz) n q y at (sy, tzx) n n q (95. 5, 19. 1) (sy, -txz) (0, -19. 1) Find C n q Find radius n

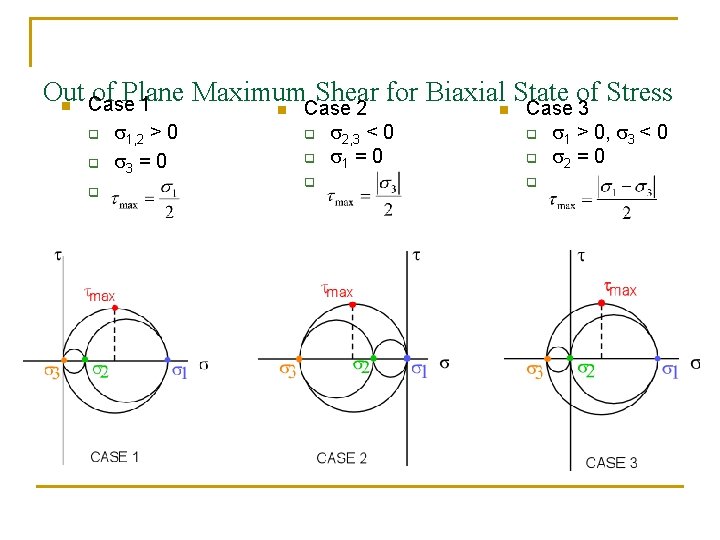
Out of Plane Maximum Shear for Biaxialn State of Stress n Case 1 n Case 2 Case 3 q q q s 1, 2 > 0 s 3 = 0 q q q s 2, 3 < 0 s 1 = 0 q q q s 1 > 0, s 3 < 0 s 2 = 0

Element A n Find principal stresses q s 1 = C + R n q s 2 = C - R n q q n 99. 2 MPa -3. 63 MPa Think about 3 -D Mohr’s Circle! This is Case #3… We want s 1 > s 2 > s 3 Assign s 2 = 0 and s 3 = -3. 63 MPa No failure theory was given, so use MDE

Element A n Find the von Mises stress (se) n Sy for our material = 331 MPa Calculate the factor of safety n q For yield

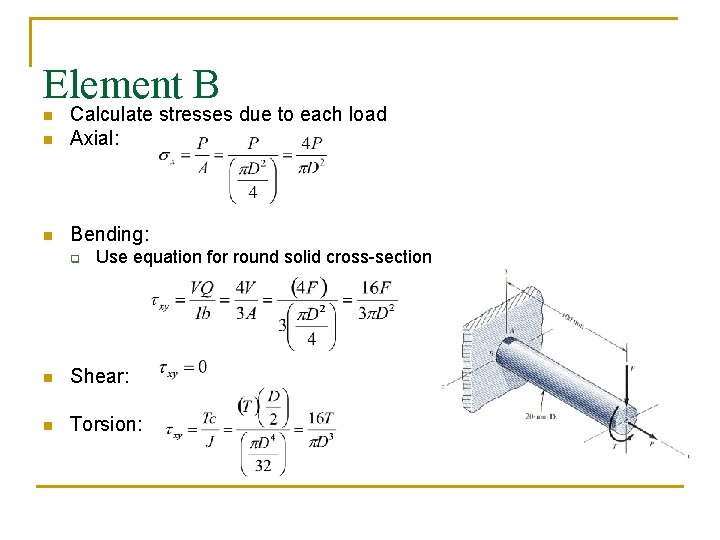
Element B n n Consider the types of loading we have Axial? q n Bending? q q n Yes – due to P Recall that bending produces s and t, depending on the element of interest Yes – due to M (s at A, t at B) Torsion? q Yes – due to T

Element B n Calculate stresses due to each load Axial: n Bending: n q Use equation for round solid cross-section n Shear: n Torsion:

Element B n n Look at a stress element Sum up stresses due to all the loads n n sx = 25. 5 MPa txy = 19. 1 MPa q Note small contribution of shear stress due to bending

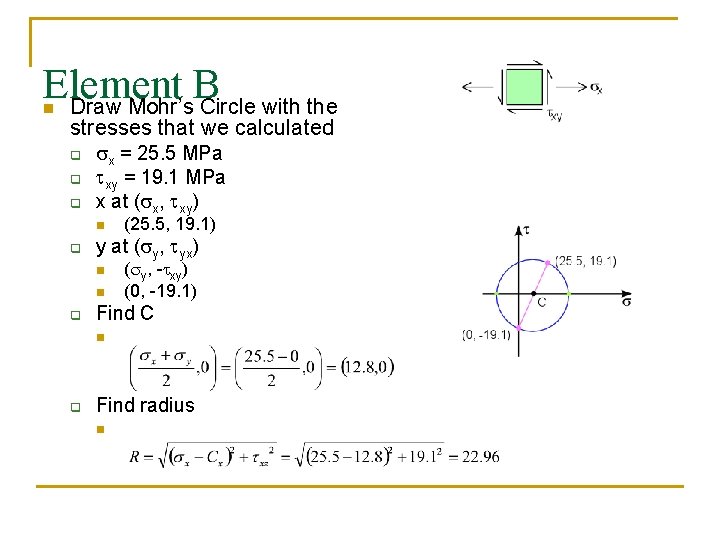
Element B Draw Mohr’s Circle with the n stresses that we calculated q q q sx = 25. 5 MPa txy = 19. 1 MPa x at (sx, txy) n q y at (sy, tyx) n n q (25. 5, 19. 1) (sy, -txy) (0, -19. 1) Find C n q Find radius n

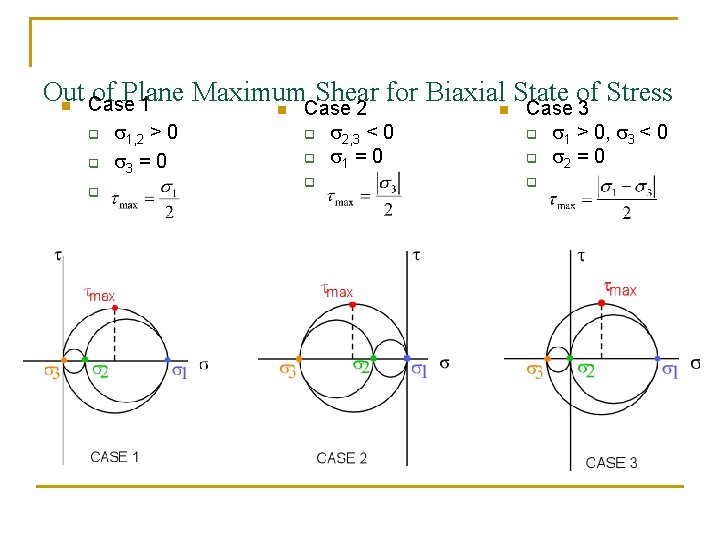
Out of Plane Maximum Shear for Biaxialn State of Stress n Case 1 n Case 2 Case 3 q q q s 1, 2 > 0 s 3 = 0 q q q s 2, 3 < 0 s 1 = 0 q q q s 1 > 0, s 3 < 0 s 2 = 0

Element B n Find principal stresses q s 1 = C + R n q s 2 = C - R n q q n 35. 8 MPa -10. 2 MPa Think about 3 -D Mohr’s Circle! This is Case #3… We want s 1 > s 2 > s 3 Assign s 2 = 0 and s 3 = -10. 2 MPa No failure theory was given, so again use MDE

Element B n Find the von Mises stress (se) n Sy for our material = 331 MPa Calculate the factor of safety n q For yield

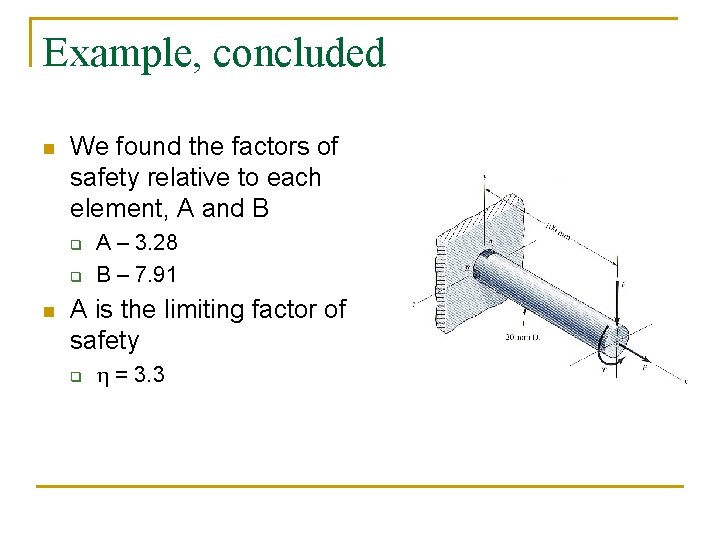
Example, concluded n We found the factors of safety relative to each element, A and B q q n A – 3. 28 B – 7. 91 A is the limiting factor of safety q = 3. 3

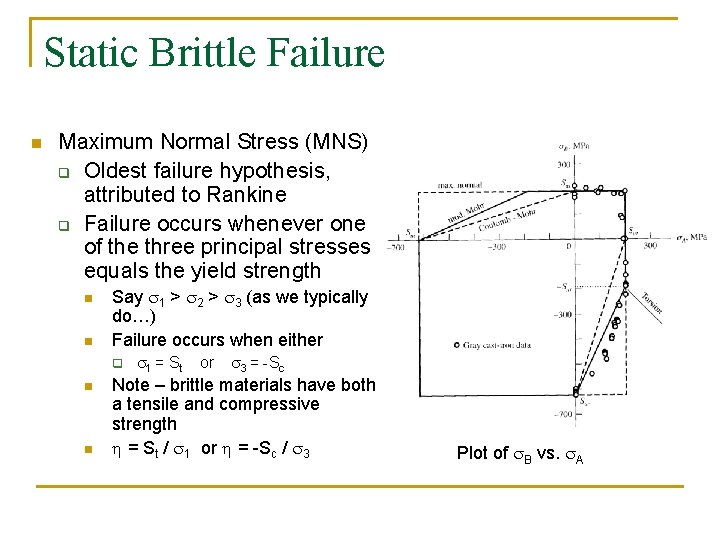
Static Brittle Failure n Three primary theories for static brittle failure q q q Maximum Normal Stress (MNS) Coulomb-Mohr Theory Modified-Mohr Theory

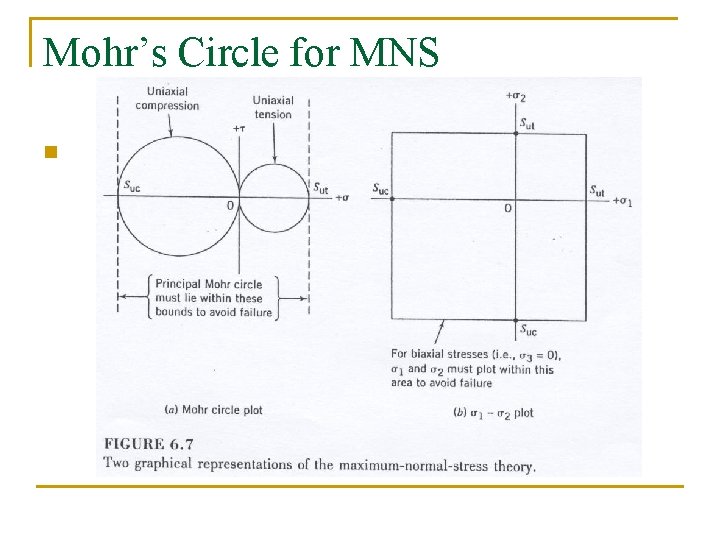
Mohr’s Circle for MNS n

Static Brittle Failure n Maximum Normal Stress (MNS) q Oldest failure hypothesis, attributed to Rankine q Failure occurs whenever one of the three principal stresses equals the yield strength n n Say s 1 > s 2 > s 3 (as we typically do…) Failure occurs when either q n n s 1 = S t or s 3 = -Sc Note – brittle materials have both a tensile and compressive strength = St / s 1 or = -Sc / s 3 Plot of s. B vs. s. A

Static Brittle Failure n Coulomb-Mohr Theory (AKA Internal Friction) Stress Region Mohr’s Circle Failure Factor of Safety Sut Suc s. A, B> 0 s. A> 0, s. B < 0 Suc s. A, B ≤ 0 Use table, or look at load line…

The Load Line – Coulomb-Mohr n s B = rs A n Then, Note: Equation of line from origin to point (s. A, s. B) “Strength” of a part can be considered the stress necessary to cause failure. To find a part’s strength at onset of failure, use h = 1.

Modified Mohr Failure Theory n

Static Brittle Failure Modified Mohr Theory n Stress Region Mohr’s Circle Failure Factor of Safety s. A, B >0 |s. B| = Sut s. A, B≤ 0 s. A > 0 -Sut < s. B < 0 s. A > 0 s. B < -Sut A: Sut See Equation A See Equation B B: Which to use? (C-M or Mod-M) In general, Mod-M is more accurate

The Load Line – Modified Mohr n s B = rs A n Then, Note: Equation of line from origin to point (s. A, s. B) Again, “strength” of a part can be considered the stress necessary to cause failure. To find a part’s strength at onset of failure, use h = 1. For both Coulomb-Mohr and Modified Mohr, you can use either the table equations or the load line equations.

Brittle Failure example n Given: q q Shaft of ASTM G 25 cast iron subject to loading shown From Table A-24 n n n Sut = 26 kpsi Suc = 97 kpsi Find: q For a factor of safety of = 2. 8, what should the diameter of the shaft (d) be?

Brittle Failure example n First, we need to find the forces acting on the shaft q Torque on shaft from pulley at B n q Torque on shaft from pulley at C n q q n TB = (300 -50)(4) = 1000 in·lb TC = (360 -27)(3) = 1000 in·lb Shaft is in static equilibrium Note that shaft is free to move along the x-axis (bearings) Draw a FBD q Reaction forces at points of attachment to show constrained motion

Equilibrium Use statics to solve for reactions forces n q q n n n RAy = 222 lb RAz = 106 lb RDy = 127 lb RDz = 281 lb OK, now we know all the forces. The problem gives us a factor of safety, but unlike our last example, we aren’t told specific places (elements) at which to look for failure! We are going to have to calculate stresses What do we need? q q Axial forces, bending moments, and torques We need to find our moments… HOW? Shear-Moment diagrams will give us the forces and moments along the shaft. Failure will likely occur where the max values are seen

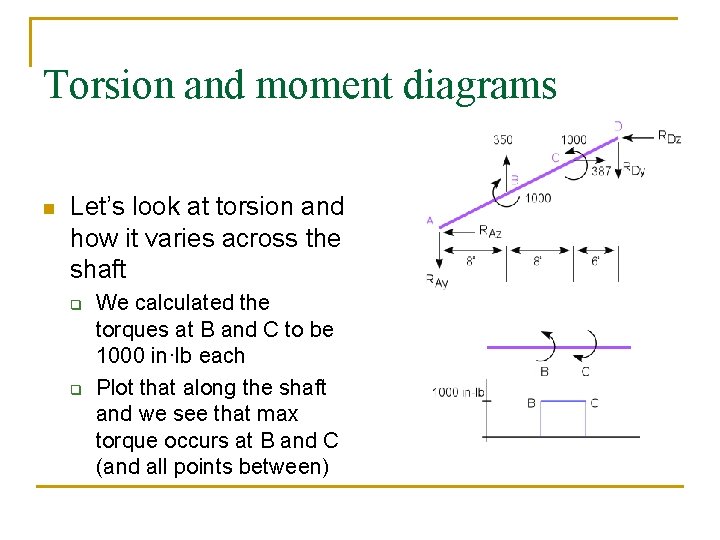
Torsion and moment diagrams n Let’s look at torsion and how it varies across the shaft q q We calculated the torques at B and C to be 1000 in·lb each Plot that along the shaft and we see that max torque occurs at B and C (and all points between)

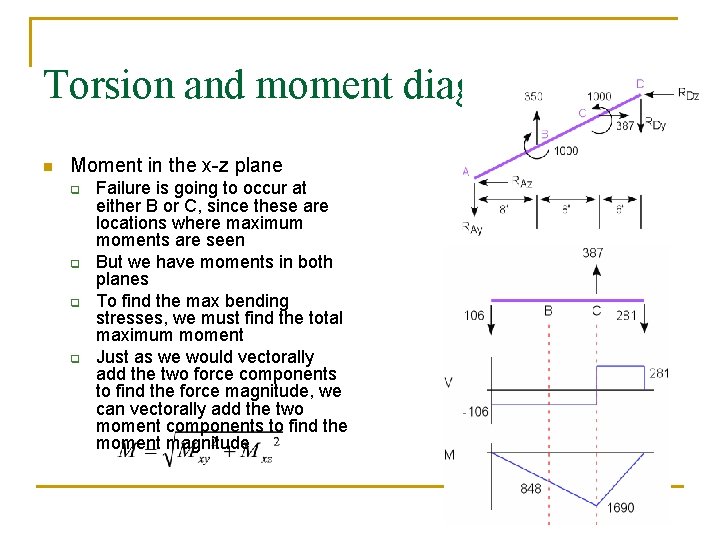
Torsion and moment diagrams n n Now let’s look at the moments We have a 3 -D loading q q n How are we going to do the V-M diagrams? Look at one plane at a time Moment in the x-y plane q From geometry you can calculate the values of the moment at B and C

Torsion and moment diagrams n Moment in the x-z plane q q Failure is going to occur at either B or C, since these are locations where maximum moments are seen But we have moments in both planes To find the max bending stresses, we must find the total maximum moment Just as we would vectorally add the two force components to find the force magnitude, we can vectorally add the two moment components to find the moment magnitude

Calculate the max moment n We found the following: q q n Calculating the magnitudes with q q n n MB x-y = 1780 in·lb MB x-z = 848 in·lb MC x-y = 762 in·lb MC x-z = 1690 in·lb MB = 1971. 7 in·lb MC = 1853. 8 in·lb Since the overall max moment is at B, we will expect failure there, and use MB in our stress calculations If we had been told the location of interest, we would essentially start here.

Calculate the stresses at B n Bending stress (s and t) q We know from experience that s is the predominant stress, so essentially we will look for failure at an element at the top of the shaft n n M = 1971 Plug in known values smax = (20 x 103)/d 3 Torsional stress q q T = 1000 t = (5. 1 x 103)/d 3

Mohr’s Circle n n Let’s look at our stress element Now construct Mohr’s circle q q n C at (10 x 103)/d 3 R = (11. 2 x 103)/d 3 s 1 = (21. 2 x 103)/d 3 s 3 = (-1. 2 x 103)/d 3 Use Coulomb-Mohr theory for brittle failure q q If making a design recommendation, you would recommend the next largest standard dimension (16 th’s) n d = 1. 375 in

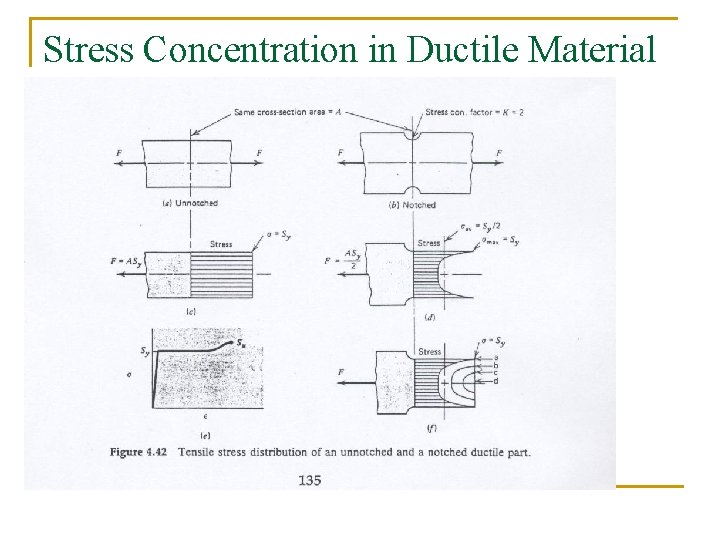
Stress concentration n A stress concentration is any geometric discontinuity in an element that is subjected to stress Aside from reducing the crosssectional area, these stress concentrations do not significantly affect static ductile failure Stress concentrations DO, however, have a significant influence on brittle failure

Analytical approach to stress concentrations n n smax = ktsnom tmax = ktstnom kt, kts are stress concentration (SC) factors snom, tnom are nominal stresses q n n Nominal – those stresses that are calculated before taking the SC’s into account SC factors are given in the text on page 982 -988 Equations for the nominal stresses (taking into account geometry change due to the SC’s) are given in the same charts

Stresses at a Hole in an Infinite Plate n

Hoop Stress at a Hole in an Infinite Plate n

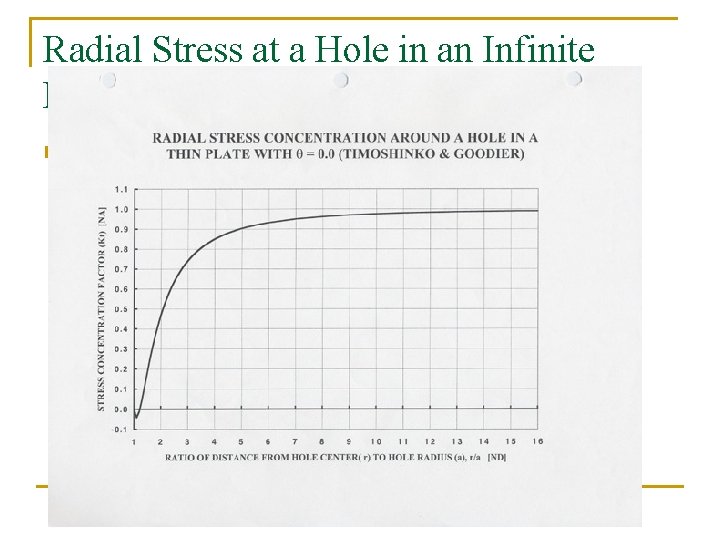
Radial Stress at a Hole in an Infinite Plate n

Stress Concentration in Ductile Material n

Residual Stresses in Ductile Material n

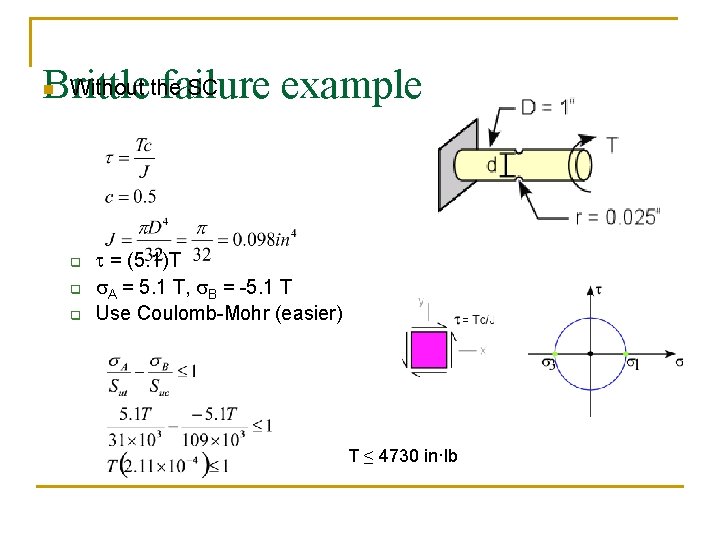
Brittle failure example n Given: q ASTM 30 cast iron n Sut = 31 ksi Suc = 109 ksi Find: q q q How much torque before failure with and without the stress concentration? Note – asked to find failure (not given a safety factor) Use = 1 to find onset of failure

Without the SC Brittle failure example n q q q t = (5. 1)T s. A = 5. 1 T, s. B = -5. 1 T Use Coulomb-Mohr (easier) T ≤ 4730 in·lb

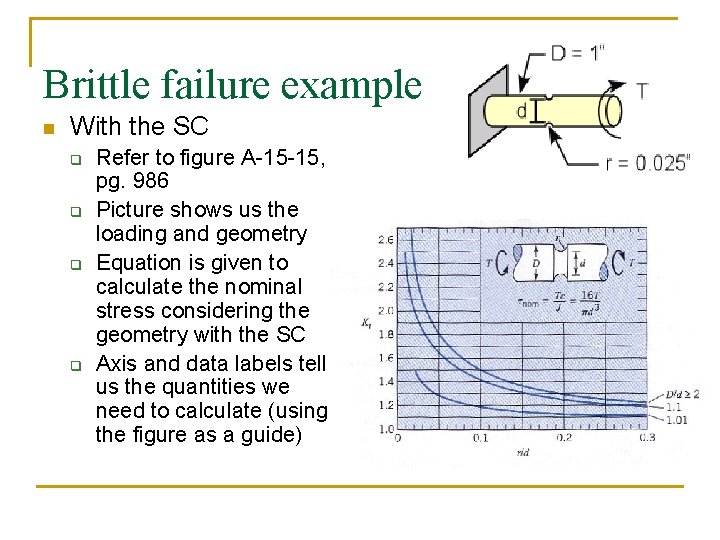
Brittle failure example n With the SC q q Refer to figure A-15 -15, pg. 986 Picture shows us the loading and geometry Equation is given to calculate the nominal stress considering the geometry with the SC Axis and data labels tell us the quantities we need to calculate (using the figure as a guide)

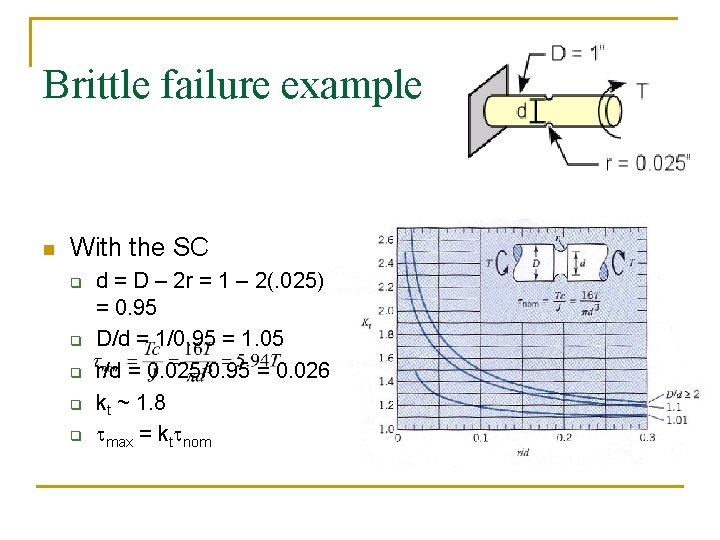
Brittle failure example n With the SC q q q d = D – 2 r = 1 – 2(. 025) = 0. 95 D/d = 1/0. 95 = 1. 05 r/d = 0. 025/0. 95 = 0. 026 kt ~ 1. 8 tmax = kttnom

Brittle failure example n n n tmax = kttnom = (1. 8)(5. 94 T) = 10. 69 T Construct stress element and Mohr’s Circle as before Use Coulomb-Mohr theory T ≤ 2258 in·lb About half the load that could be withstood in the absence of the SC!

What if wefailure consider a solid shaft (no Brittle example SC’s) with a diameter of d (0. 95) ? n n Again, use Coulomb-Mohr n Note, this is a greater amount of torque than a shaft with larger diameter but with a SC

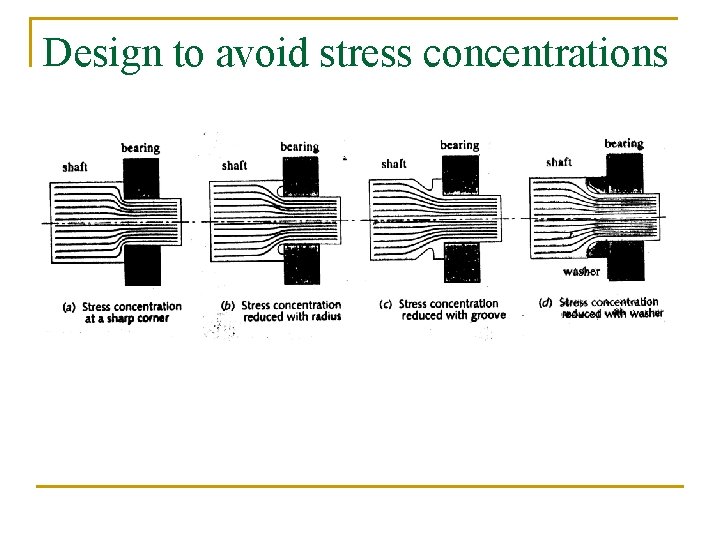
Design to avoid stress concentrations n n n Avoid sudden changes in cross-section Avoid sharp inside corners Force-flow analogy q q Imagine flow of incompressible fluid through part Sudden curvature in streamlines… n High stress concentration!

Design to avoid stress concentrations

Design to avoid stress concentrations