MATRIX 1 DEFINITION Matrix is rectangular array of






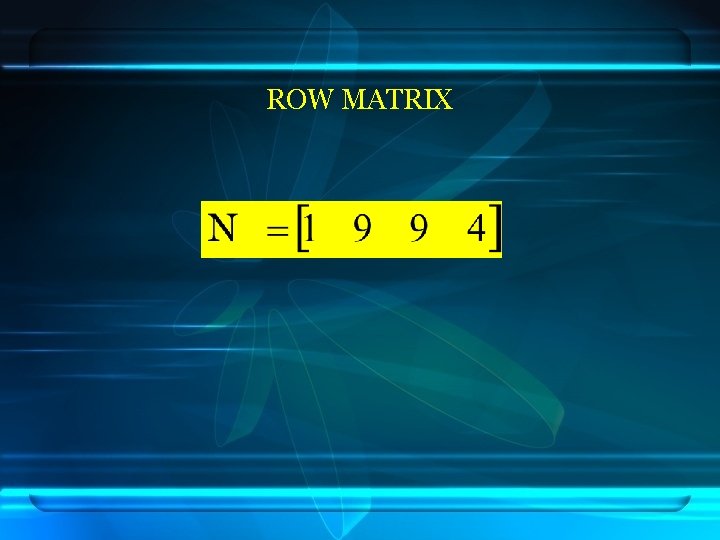






















- Slides: 61

MATRIX 1

DEFINITION Matrix is rectangular array of numbers, consists of rows and columns and is written using brackets or parentheses.

NOTATION OF MATRIX

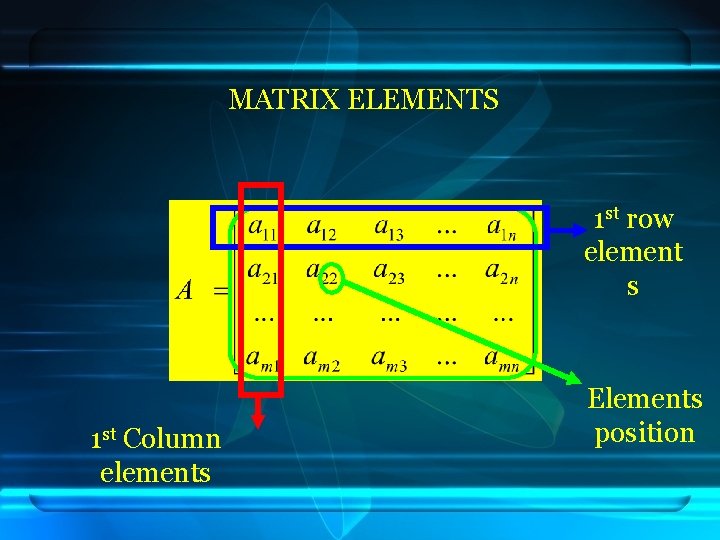
MATRIX ELEMENTS 1 st row element s 1 st Column elements Elements position

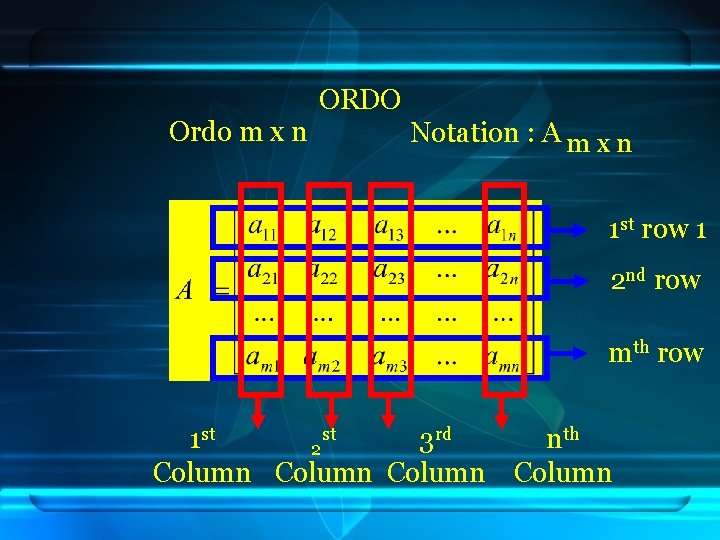
Ordo m x n ORDO Notation : A m x n 1 st row 1 2 nd row mth row st rd 1 st 3 2 Column nth Column

Example: 1. What is the name of matrix above?

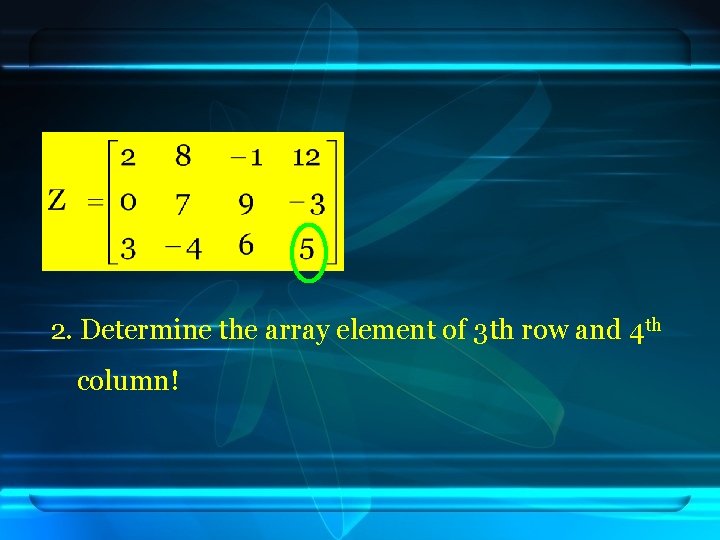
2. Determine the array element of 3 th row and 4 th column!

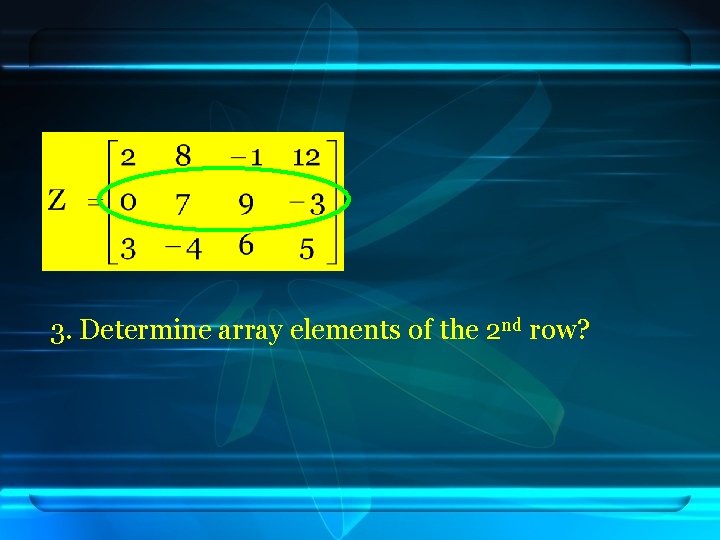
3. Determine array elements of the 2 nd row?

3. Determine dimension of Matrix Z! Ordo 3 x 4 Notation Z 3 x 4

TYPES OF MATRIX 10
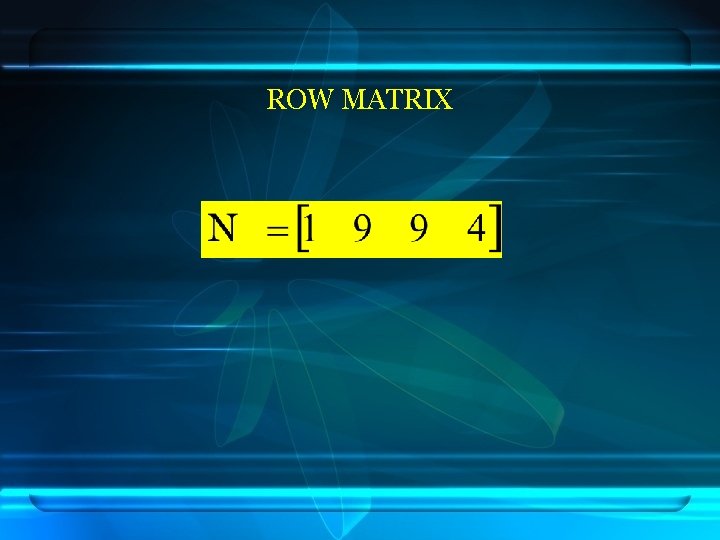
ROW MATRIX

COLUMN MATRIX

DIAGONAL MATRIX

IDENTITY MATRIX Addition Zero Matrix Multiplication

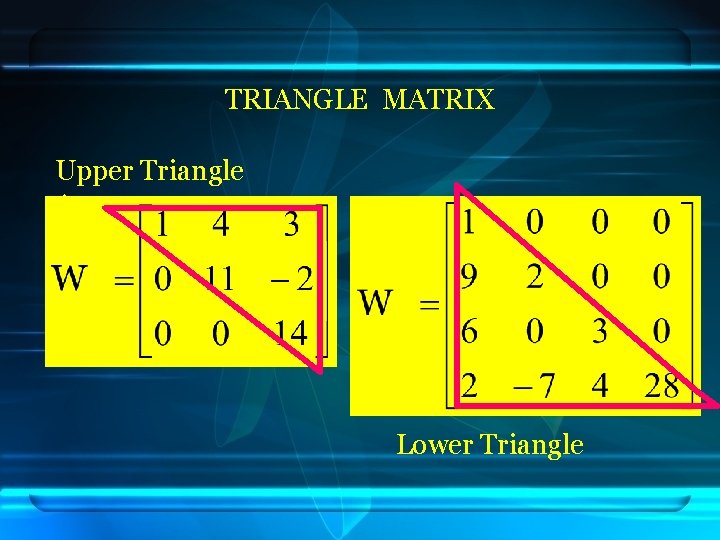
TRIANGLE MATRIX Upper Triangle Atas Lower Triangle

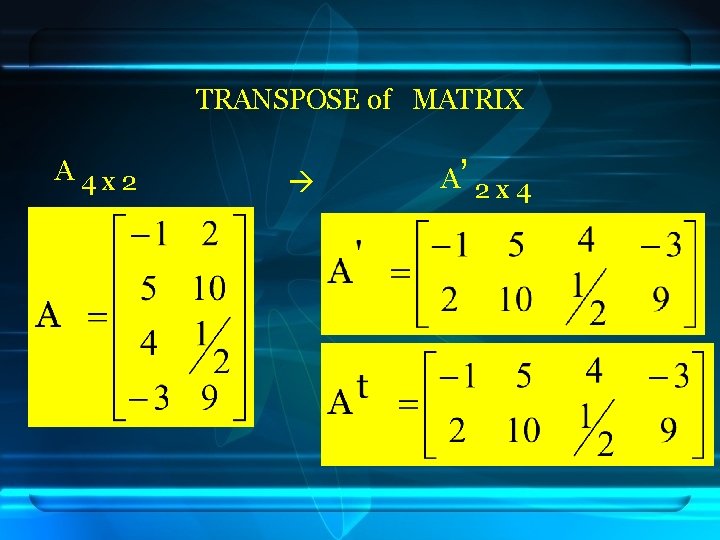
MATRIX TRANSPOSE Transpose matriks A happened if each elements of row matrix A change be come element of column of matrix A’, so A m x n become A’ n x m. 1 st row elements A 1 st column elements A’, 2 nd row elements A 2 nd column elements A’, etc

TRANSPOSE of MATRIX A 4 x 2 A’ 2 x 4

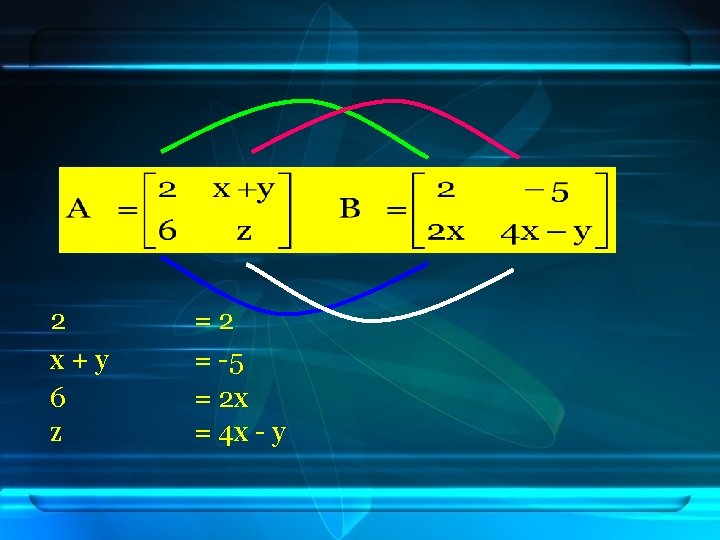
SIMILARITY OF TWO MATRIX Giveb If A = B, determine the value of x, y dan z!

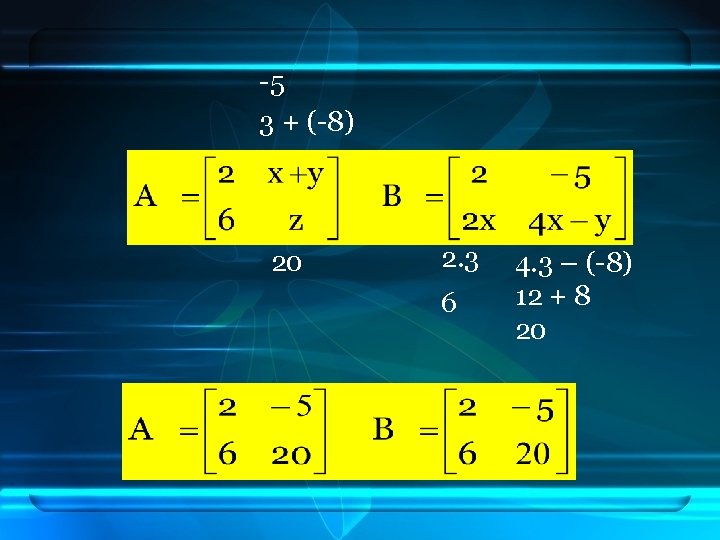
2 x+y 6 z =2 = -5 = 2 x = 4 x - y


-5 3 + (-8) 20 2. 3 6 4. 3 – (-8) 12 + 8 20

1. ADDITION AND SUBSTRACTION OF MATRIX Two or more matriks can be addition or subtraction if : a. Both of them have same Ordo b. Operated only for elements in the similar position

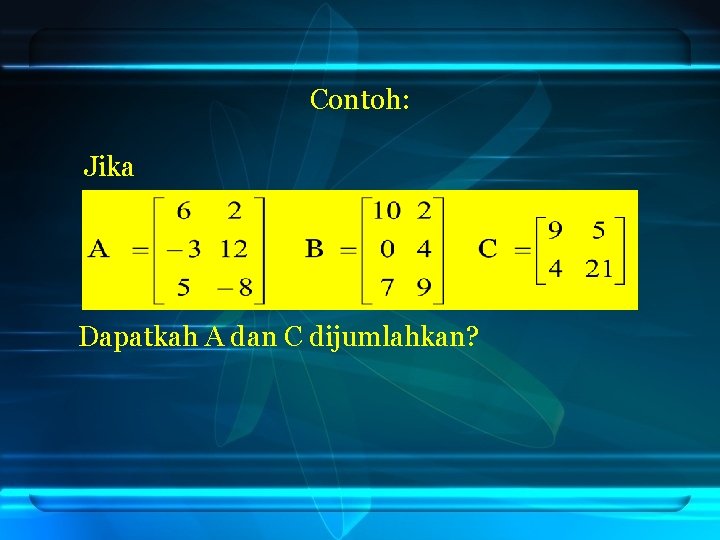
Contoh: Jika Dapatkah A dan C dijumlahkan?

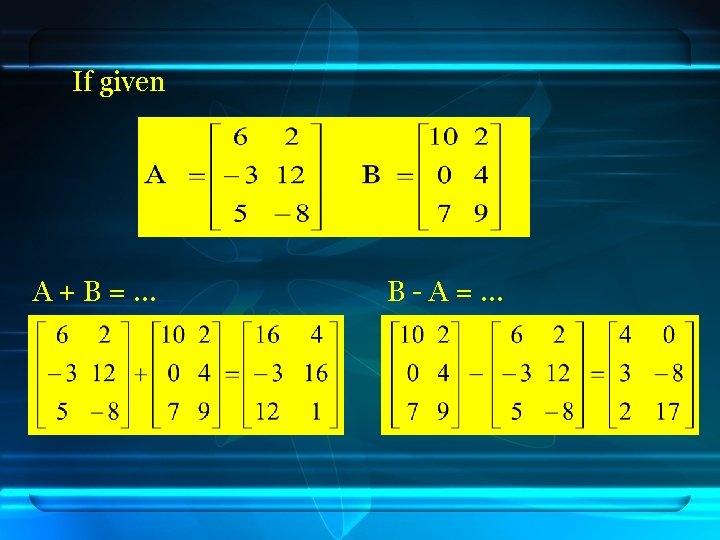
If given A+B=… B-A=…

2. MULTIPLICATION OF MATRIX a. Multiplication two matrices =

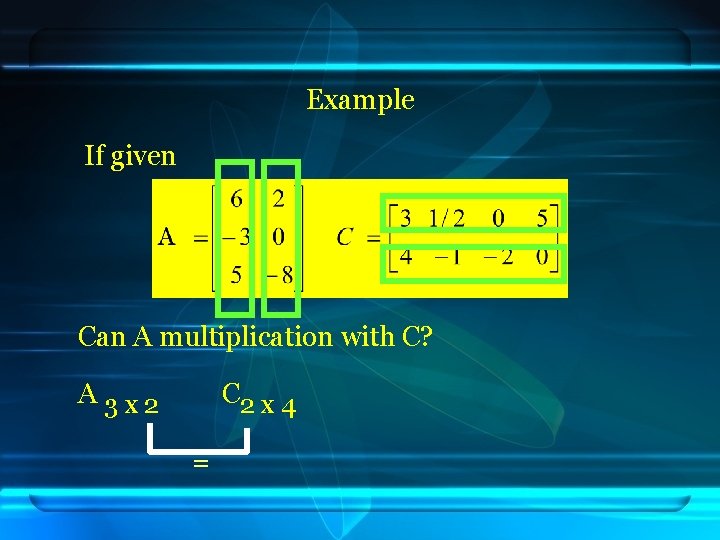
Example If given Can A multiplication with C? A 3 x 2 C 2 x 4 =

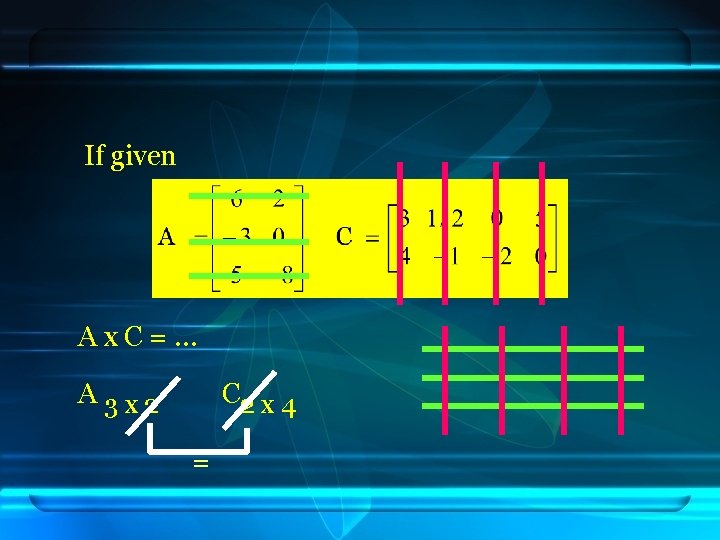
If given Ax. C=… A 3 x 2 C 2 x 4 =

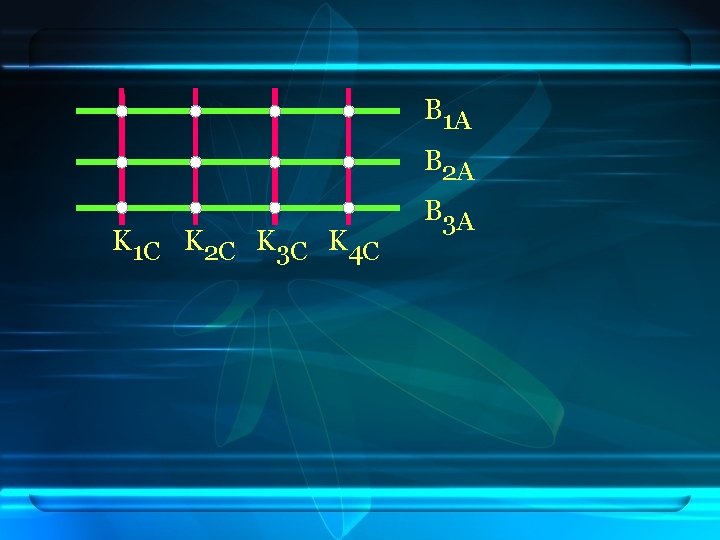
B 1 A B 2 A K 1 C K 2 C K 3 C K 4 C B 3 A

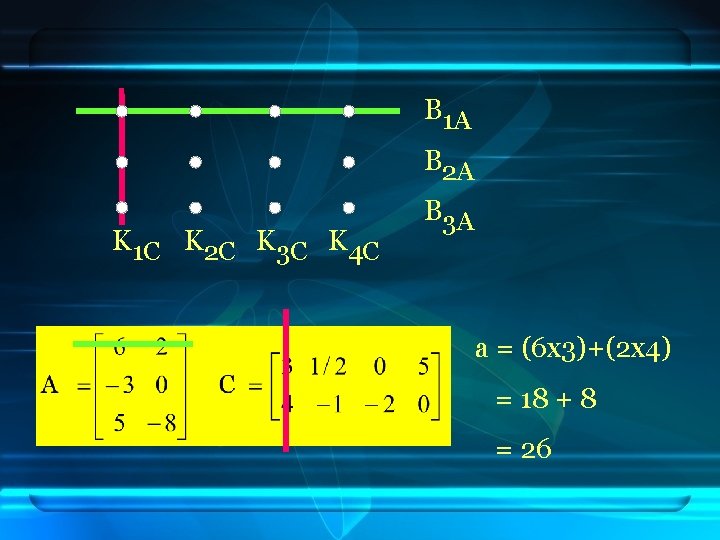
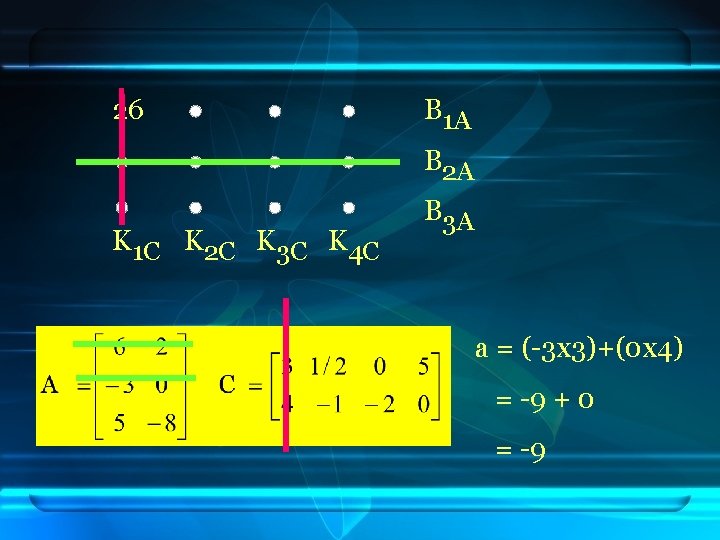
B 1 A B 2 A K 1 C K 2 C K 3 C K 4 C B 3 A a = (6 x 3)+(2 x 4) = 18 + 8 = 26

26 B 1 A B 2 A K 1 C K 2 C K 3 C K 4 C B 3 A a = (-3 x 3)+(0 x 4) = -9 + 0 = -9

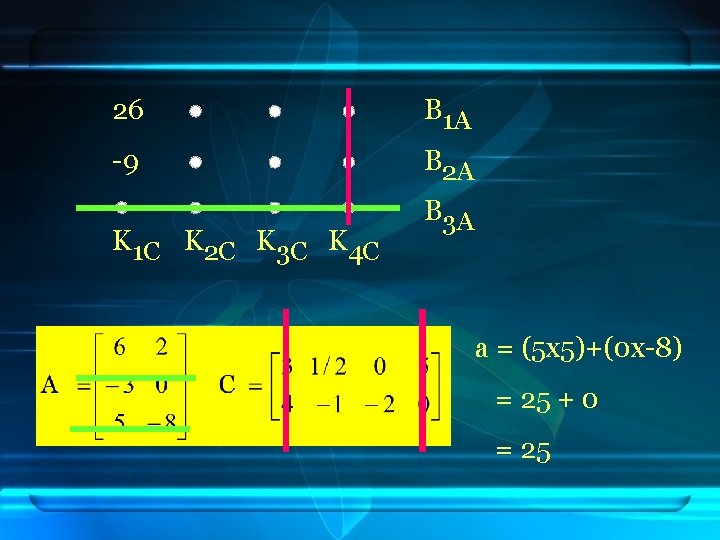
26 B 1 A -9 B 2 A K 1 C K 2 C K 3 C K 4 C B 3 A a = (5 x 5)+(0 x-8) = 25 + 0 = 25

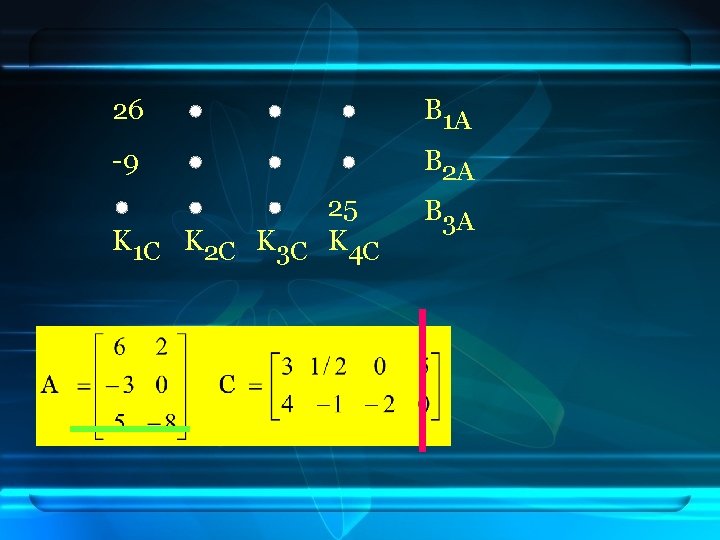
26 B 1 A -9 B 2 A 25 K 1 C K 2 C K 3 C K 4 C B 3 A

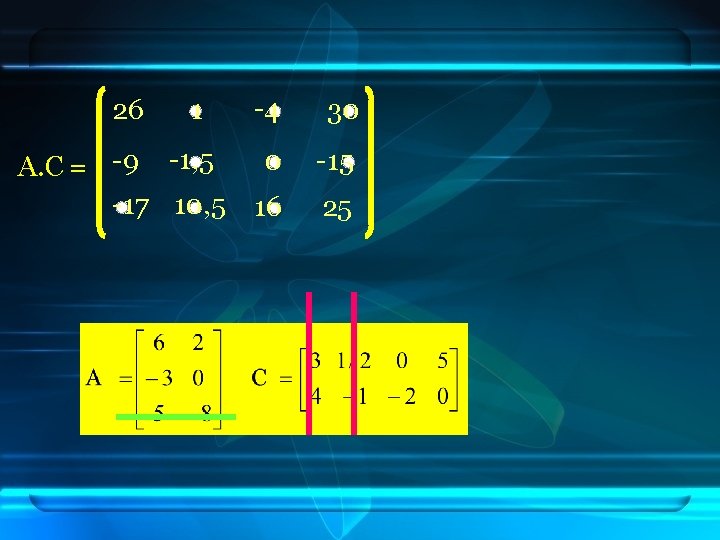
26 1 A. C = -9 -1, 5 -17 10, 5 -4 30 0 -15 16 25

b. Scale multiplication with matrix Multiplication a real number with matrix A is multipilcation each elements of matrix A by that real number k. A = [k. amn]

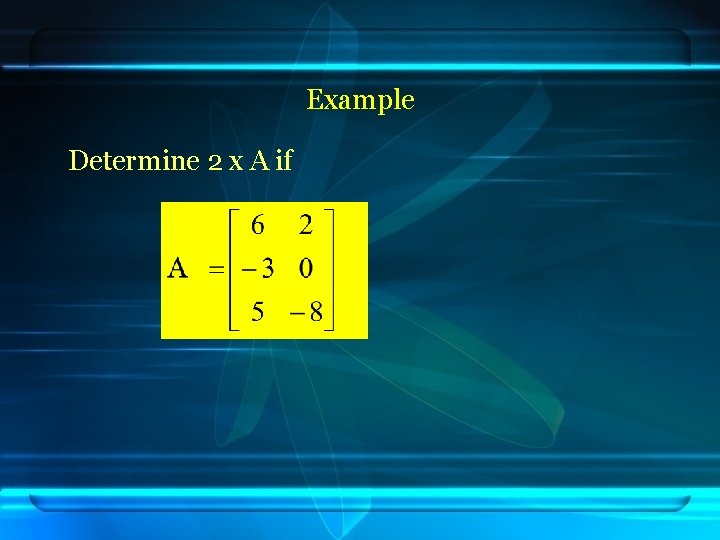
Example Determine 2 x A if

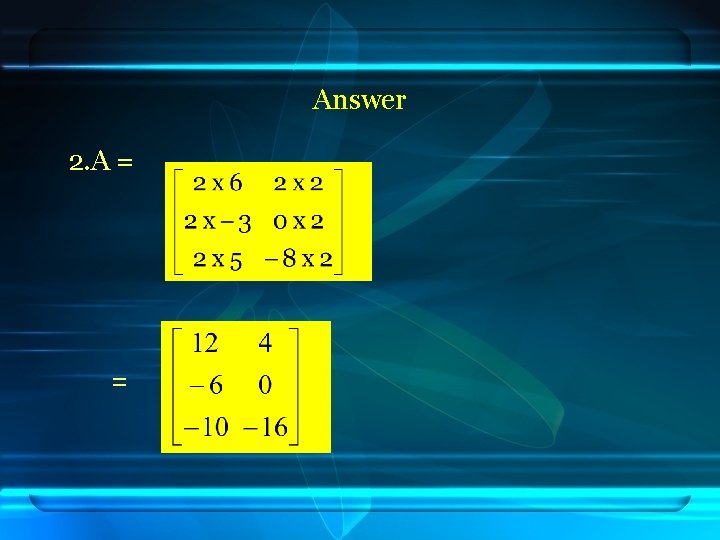
Answer 2. A = =

DETERMINANT Determinant of matrix a. Only used in square b. are substraction with elements 1 st diagonal and 2 nd diagonal, where each elements enclosed

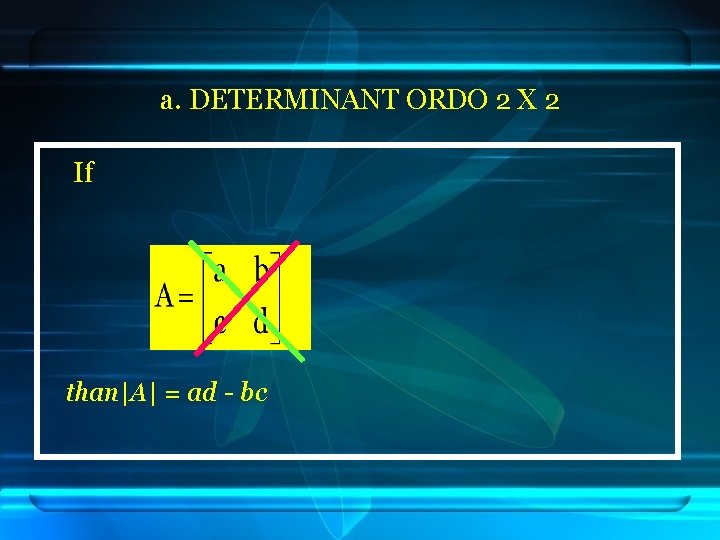
a. DETERMINANT ORDO 2 X 2 If than|A| = ad - bc

Example Determine value of determinant matrix below Answer: |A| = 5. 6 – 10. -1 = 30 + 10 = 40

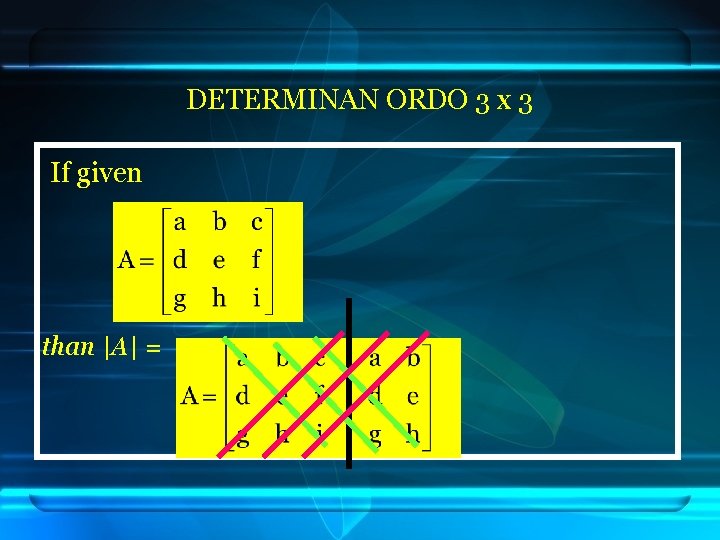
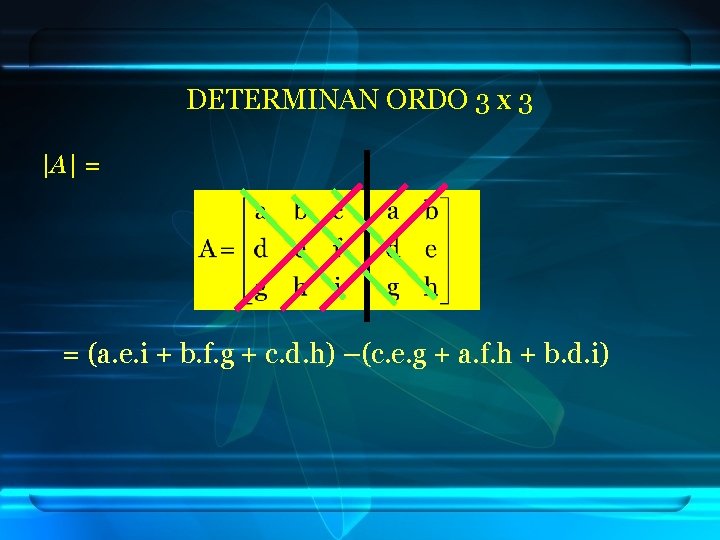
DETERMINAN ORDO 3 x 3 If given than |A| =

DETERMINAN ORDO 3 x 3 |A| = = (a. e. i + b. f. g + c. d. h) –(c. e. g + a. f. h + b. d. i)

Example Determine determinat of Answer: = (0. 1. 5 + 4. -3. -1 + 7. 2. 3) –(-1. 1. 7 +3. -3. 0 + 5. 2. 4) = (0+12+42) – (-7+0+40) = 54 – 33 = 21

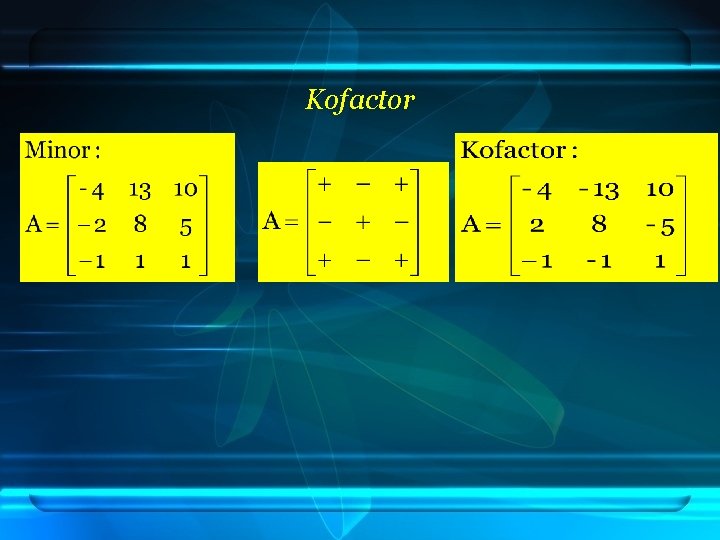
4. ADJOIN Adjoin matrix A is the result transpose from kofaktor matriks A. Matrix A Minor Matrix A Kofaktor Matrix A Adjoin Matrix A

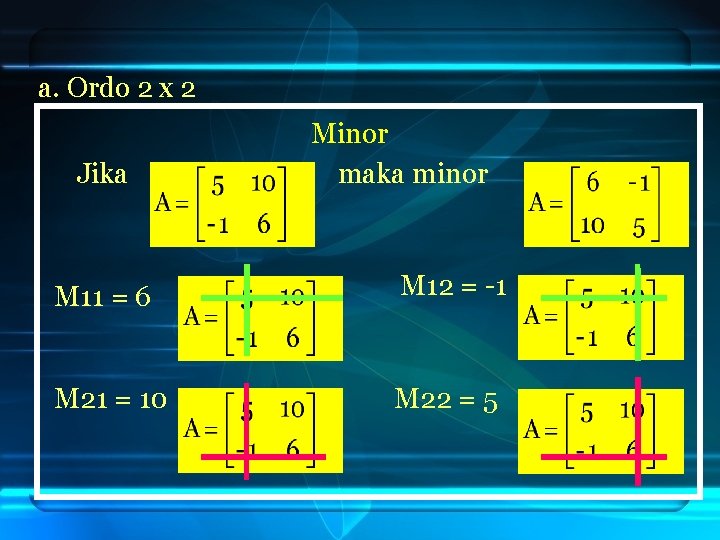
a. Ordo 2 x 2 Jika Minor maka minor M 11 = 6 M 12 = -1 M 21 = 10 M 22 = 5

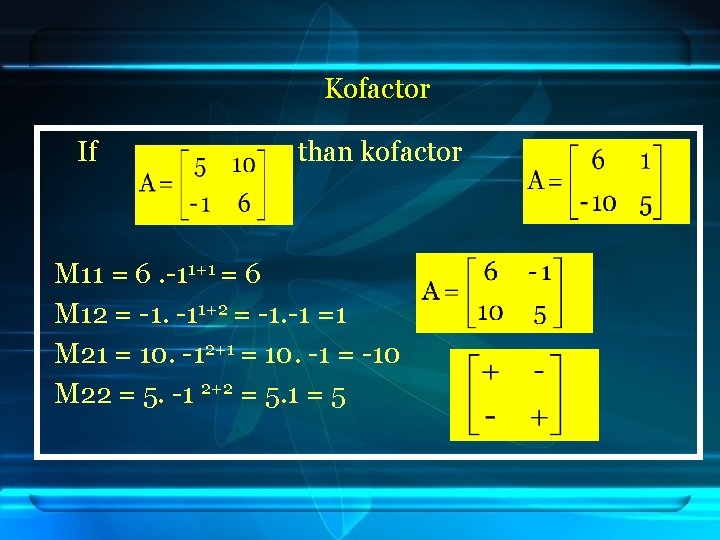
Kofactor If than kofactor M 11 = 6. -11+1 = 6 M 12 = -1. -11+2 = -1. -1 =1 M 21 = 10. -12+1 = 10. -1 = -10 M 22 = 5. -1 2+2 = 5. 1 = 5

Adjoin If than Adjoin matrix A Resulted from the its kofactor

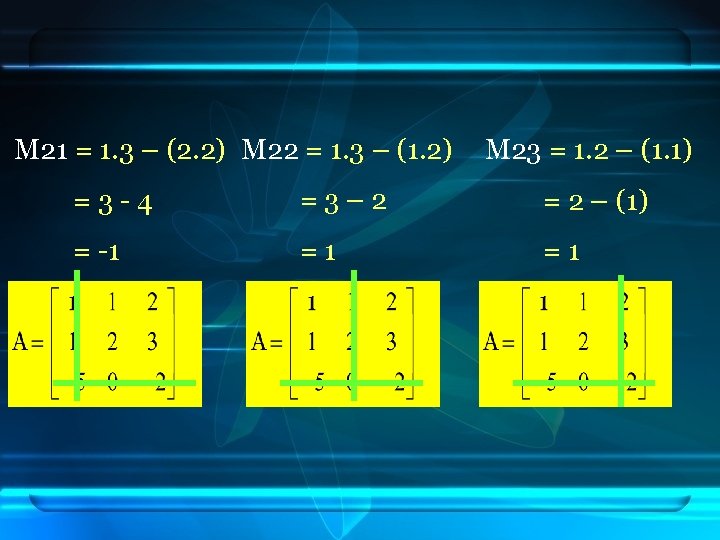
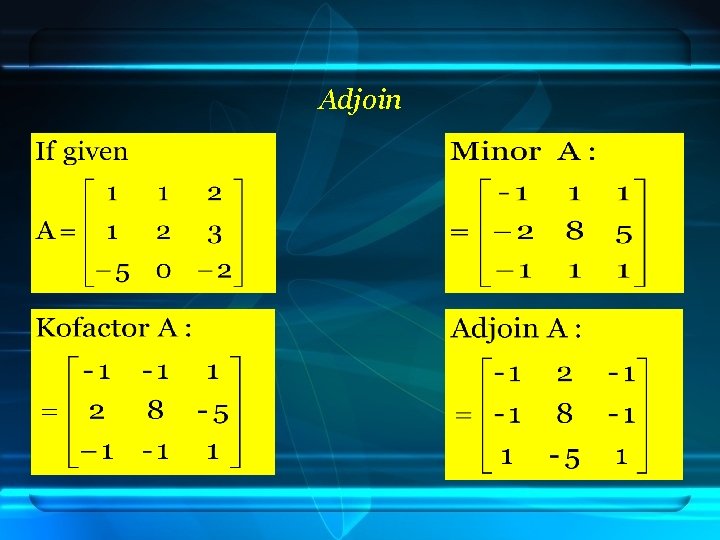
b. Ordo 3 x 3 If , minor matrix A showed next M 11 = 2. -2 – (0. 3) M 12 = 1. -2 – (-5. 3) M 13 = 1. 0 – (-5. 2) = -4 - 0 = -2 – (-15) = 0 – (-10) = -4 = 13 = 10



Kofactor

Adjoin

5. INVERSE Inverse matrix A

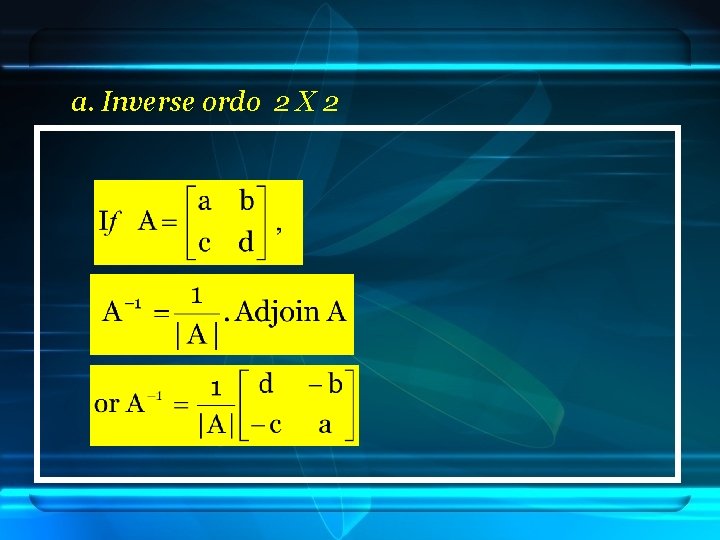
a. Inverse ordo 2 X 2

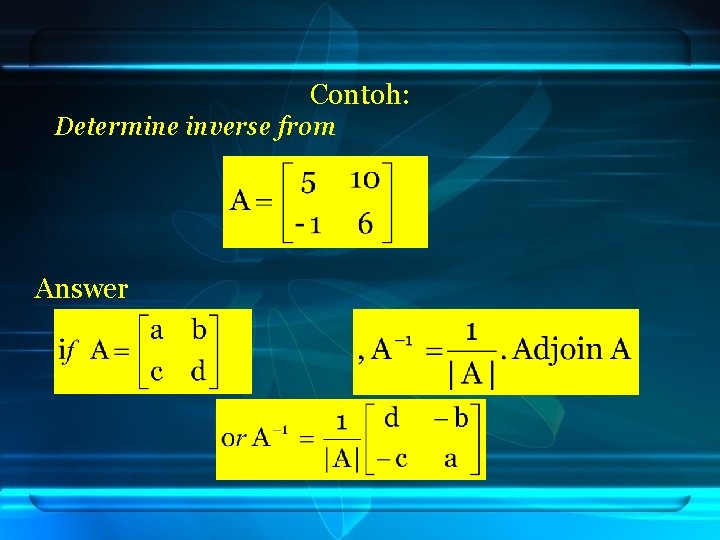
Contoh: Determine inverse from Answer

Answer :


II. MATRIX APPLICATION Using to determine variabel value of linear equation. If the equation have variabel x dan y, than. .

Example Determine value of x dan y from the next equations 2 x + 3 y =7 x - 2 y =7


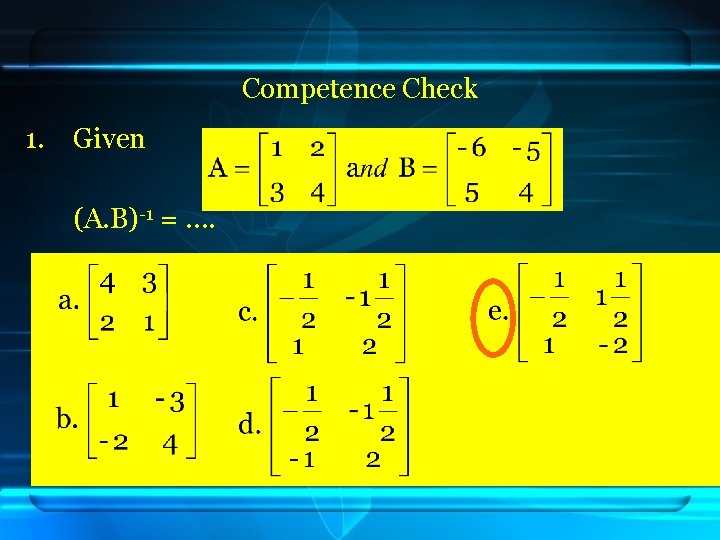
Competence Check 1. Given (A. B)-1 = ….

2. Determine solution set from the next l are ….