MATHMATIQUES DISCRTES Chapitre 6 relations Franois Meunier DMI

MATHÉMATIQUES DISCRÈTES Chapitre 6 (relations) François Meunier DMI

Relations Des objets mathématiques qui spécifient et décrivent des relations entre des éléments d’un ensemble ou plusieurs ensembles. l Une fonction f qui projette un ensemble A sur un ensemble B assigne exactement un élément de B à chaque élément de A. l Les relations n’ont pas de restriction. Un élément dans A peut être assigné à plus qu’un élément dans B. l Les relations sont des généralisations des fonctions; elles peuvent être utilisées pour exprimer une plus grande classe de relations entre ensembles. l

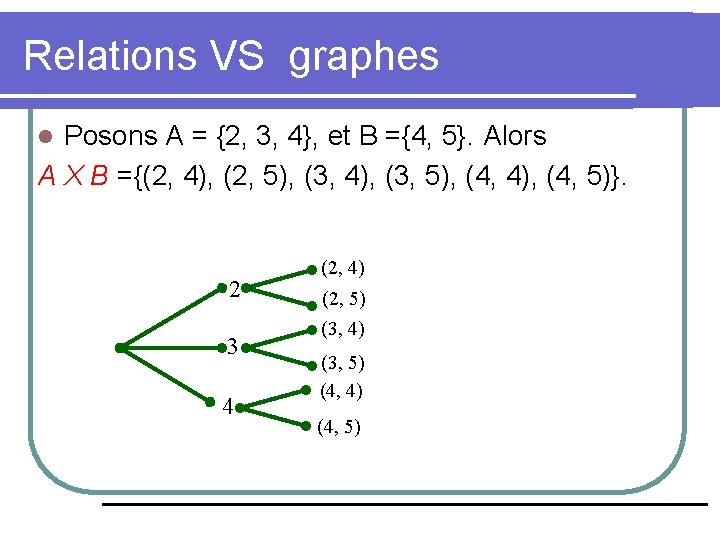
Relations binaires Avec A, B des ensembles. Les relations entre les éléments de ces deux ensembles sont représentés par une Relation binaire. l i. e. une relation binaire de A à B est un ensemble R où a R b dénote (a, b) ∈ R. a est en relation avec b par R. R AXB l Les éléments de A X B et R sont des paires ordonnées puisque le premier élément de l’ensemble vient de l’ensemble A et le second élément de l’ensemble B. l l Posons A = {2, 3, 4}, et B ={4, 5}. Alors A X B ={(2, 4), (2, 5), (3, 4), (3, 5), (4, 4), (4, 5)}.

Relations VS graphes Posons A = {2, 3, 4}, et B ={4, 5}. Alors A X B ={(2, 4), (2, 5), (3, 4), (3, 5), (4, 4), (4, 5)}. l 2 3 4 (2, 4) (2, 5) (3, 4) (3, 5) (4, 4) (4, 5)

Relations binaires Posons A = {2, 3, 4}, et B ={4, 5}. Alors A X B ={(2, 4), (2, 5), (3, 4), (3, 5), (4, 4), (4, 5)}. Autres relations de A à B: l l l l l i) Ø ii) {(2, 4)} iii) {(2, 4), (2, 5)} iv) {(2, 4), (3, 4), (4, 4)} v) {(2, 4), (3, 4), (4, 5)} vi) A X B Pour des ensembles finis A, B avec |A| = m et |B| = n, il existe 2 mn relations de A à B, incluant la relation vide et la relation A X B elle-même.

Propriétés des Relations l La relation de A sur A i. e. A X A est une relation binaire sur A. l Cette relation est Réflexive, si chaque élément a de A est en relation avec luimême. l R sur A est réflexive si ∀a ((a, a) ∈ R) où A est l’univers du discours.

Propriétés des Relations l l Posons A = {1, 2, 3, 4} R 1 et R 2 sont des relations réflexives puisqu’elles contiennent toutes les paires de la forme (a, a). R 1 = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)}. R 2 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}.

Propriétés des Relations La relation R sur A est symétrique si (a, b) ∈ R ⇒ (b, a) ∈ R, pour tout a, b ∈ A l Posons A={1, 2, 3} l R 1 = {(1, 2), (2, 1), (1, 3), (3, 1)}. symétrique l R 2= {(1, 1), (2, 2), (3, 3), (2, 3), (3, 2)}. réflexive et symétrique l R 3= {(1, 1), (2, 3), (3, 3)}. Non réflexive et non symétrique. l

Propriétés des Relations l Une relation R sur A est antisymétrique si (a, b) R et (b, a) R seulement quand a = b l Aussi exprimée par: a≠b, (a, b) R → (b, a) R. l Une relation R sur A est asymétrique si (a, b) R implique (b, a) R pour tout a, b A.

Antisymmétrie l Les termes symétrie et antisymétrie ne sont pas opposés, puisqu’une relation peut avoir les deux propriétés ou ne pas les avoir. l Une relation ne peut avoir ces deux propriétés si elle contient des paires de la forme (a, b) où a ≠ b. l Symétrie et Asymétrie, sont opposées.

Symétrie - Antisymétrie l. A = {1, 2, 3, 4} R 1 = {(1, 1), (1, 2), (2, 1)} Symétrique R 2 = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)} Symétrique R 3 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)} Antisymétrique R 4 = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)} Asymétrique

Transitivité l Une relation R est transitive ssi (pour tout a, b, c) (a, b) R (b, c) R → (a, c) R. l Donc si a est “ en relation avec ” b et b est “en relation avec ” c, alors a est “en relation avec ” c avec b jouant le rôle d’ “intermédiaire”. l Ex: A = {1, 2, 3, 4) R = {(2, 1), (3, 2), (4, 1), (4, 2), (4, 3)}

Combiner des Relations l Les relations sont des ensembles, et par conséquent, nous pouvons appliquer les opérations usuelles sur les ensembles sur ces relations. l Si nous avons deux relations R 1 et R 2, et chacune d’elle provient d’un ensemble A appliquée à un ensemble B, alors nous pouvons les combiner comme: R 1 U R 2, R 1 ∩ R 2, ou R 1 – R 2. l Dans chaque cas, le résultat donne une autre relation de A à B.

Combinaisons de Relations: Exemple l Posons A = {1, 2, 3} et B = {1, 2, 3, 4} R 1 ={(1, 1), (2, 2), (3, 3)} R 2 = {(1, 1), (1, 2), (1, 3), (1, 4)} R 1∪ R 2={(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (3, 3)} R 1∩ R 2={(1, 1)} R 1 – R 2={(2, 2), (3, 3)} R 2 – R 1={(1, 2), (1, 3), (1, 4)}

Combiner des Relations Autre approche pour combiner des relations. l Définition: Posons R une relation entre A et B et S une relation entre B et C. La composition de R et S est une relation consistant de paires ordonnées (a, c), où a A, c C, et pour lequel un élément b B tel que (a, b) R et (b, c) S. LA composition de R et S est exprimée par S R. l Donc, si la relation R contient une paire (a, b) et la relation S contient une paire (b, c), alors S R contient une paire (a, c). l

Combiner des Relations Exemple: Posons D et S des relations sur A = {1, 2, 3, 4}. D = {(a, b) | b = 5 - a} “b égal (5 – a)” S = {(a, b) | a < b} “a est plus petit que b” l D = {(1, 4), (2, 3), (3, 2), (4, 1)} S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)} S D = {(2, 4), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)} l D projette un élément a à l’élément (5 – a), ensuite S projette (5 – a) à tous les éléments que (5 – a), résultant à S D = {(a, b) | b>5 – a} ou S D = {(a, b) | a + b>5}.

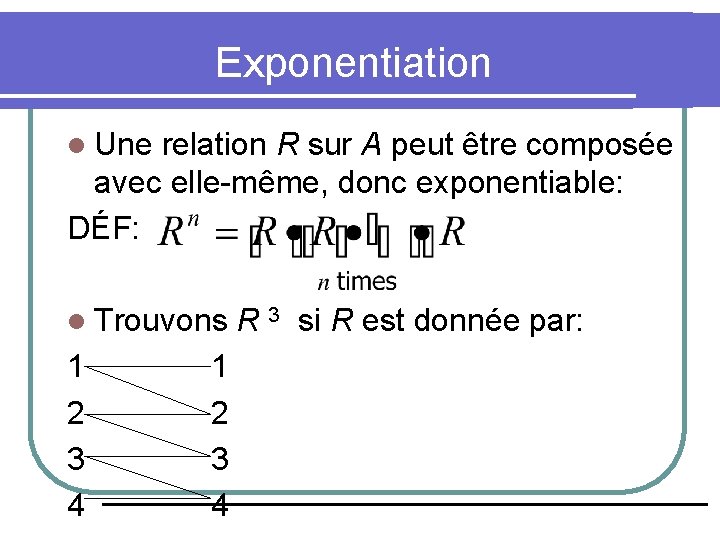
Combiner des Relations Définition: Posons R une relation sur A. l. La puissance Rn, n = 1, 2, 3, …, est définie de façon inductive par: l R 1 = R l Rn+1 = Rn R l l La composition multiples de R: l Rn = R R … R (n fois la relation R)

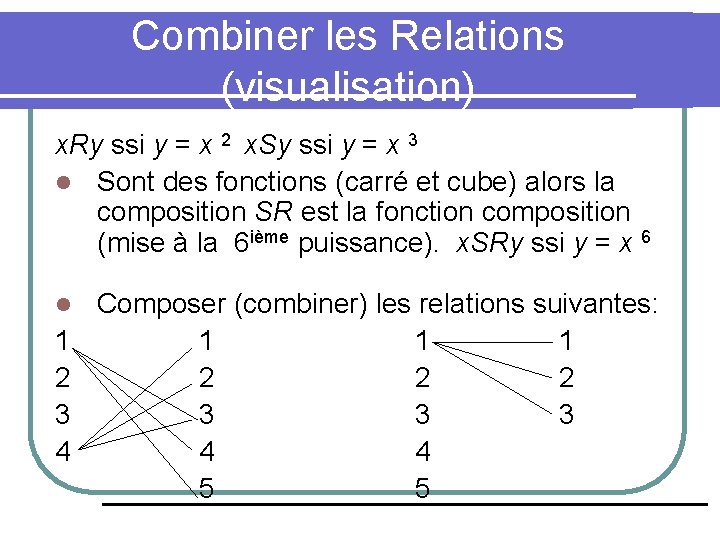
Combiner des Relations Supposons: R définie sur N par: x. Ry ssi y = x 2 et S définie sur N par: x. Sy ssi y = x 3 l Quelle est la relation composée SR ? l

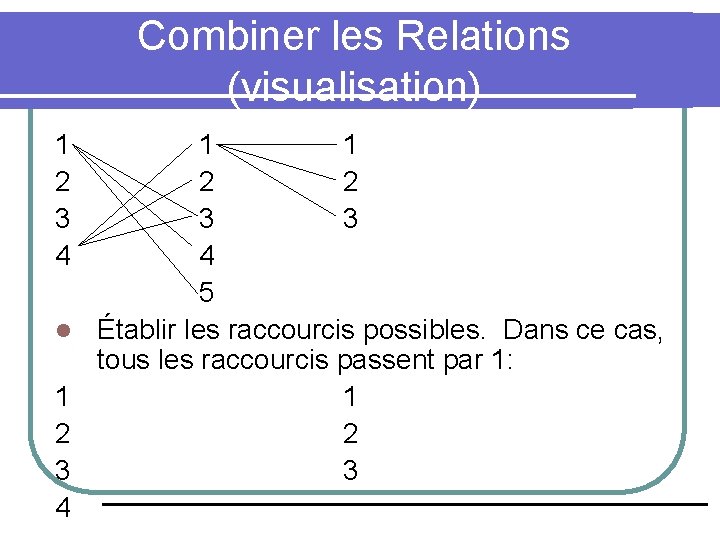
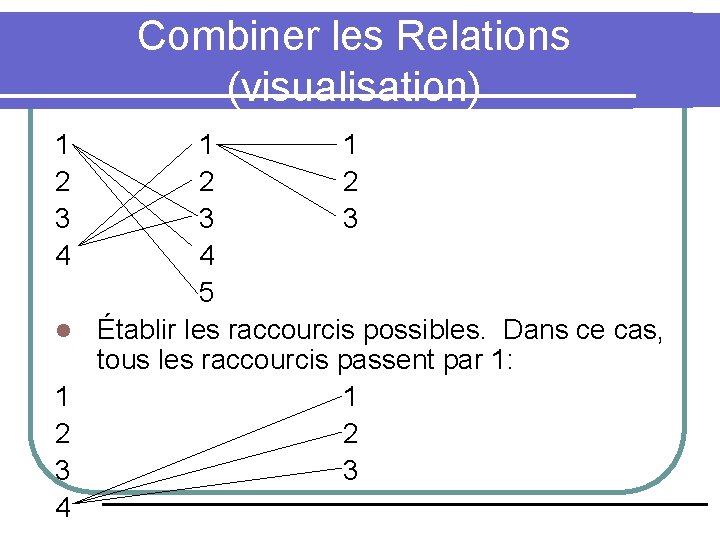
Combiner les Relations (visualisation) x. Ry ssi y = x 2 x. Sy ssi y = x 3 l Sont des fonctions (carré et cube) alors la composition SR est la fonction composition (mise à la 6 ième puissance). x. SRy ssi y = x 6 l 1 2 3 4 Composer (combiner) les relations suivantes: 1 1 1 2 2 2 3 3 3 4 4 5 5

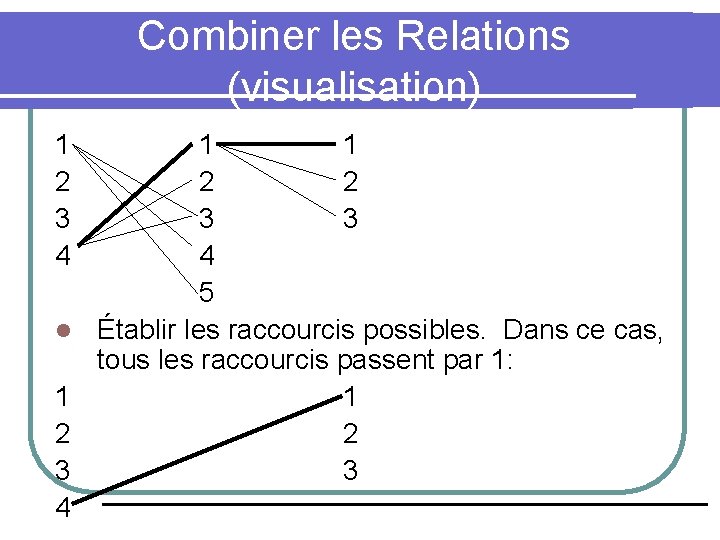
Combiner les Relations (visualisation) 1 2 3 4 l 1 2 3 4 1 1 2 2 3 3 4 5 Établir les raccourcis possibles. Dans ce cas, tous les raccourcis passent par 1: 1 2 3

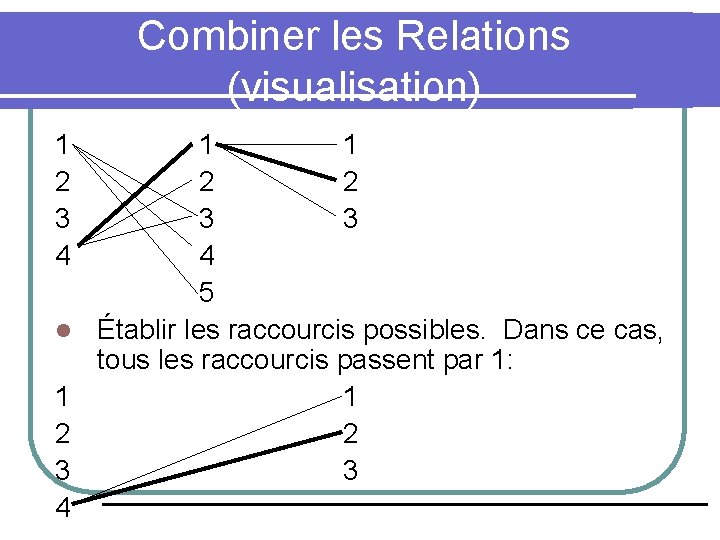
Combiner les Relations (visualisation) 1 2 3 4 l 1 2 3 4 1 1 2 2 3 3 4 5 Établir les raccourcis possibles. Dans ce cas, tous les raccourcis passent par 1: 1 2 3

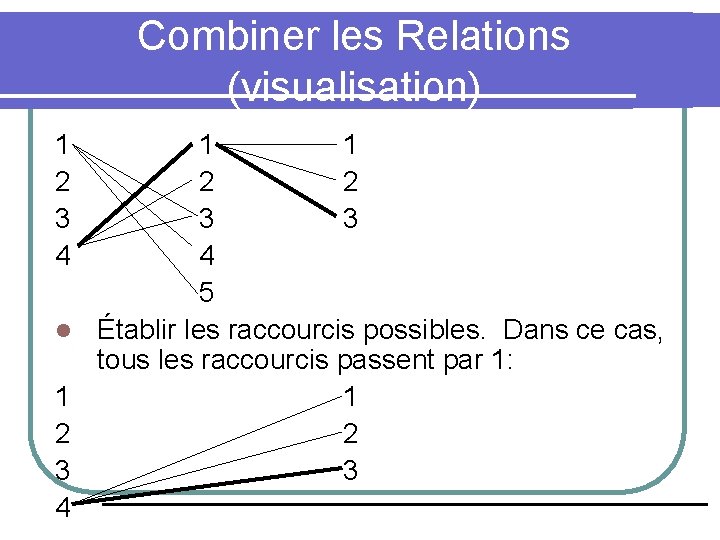
Combiner les Relations (visualisation) 1 2 3 4 l 1 2 3 4 1 1 2 2 3 3 4 5 Établir les raccourcis possibles. Dans ce cas, tous les raccourcis passent par 1: 1 2 3

Combiner les Relations (visualisation) 1 2 3 4 l 1 2 3 4 1 1 2 2 3 3 4 5 Établir les raccourcis possibles. Dans ce cas, tous les raccourcis passent par 1: 1 2 3

Combiner les Relations (visualisation) 1 2 3 4 l 1 2 3 4 1 1 2 2 3 3 4 5 Établir les raccourcis possibles. Dans ce cas, tous les raccourcis passent par 1: 1 2 3

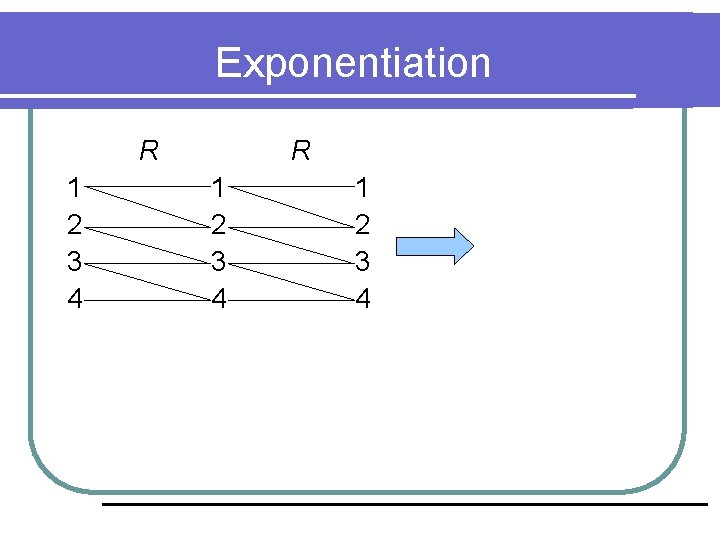
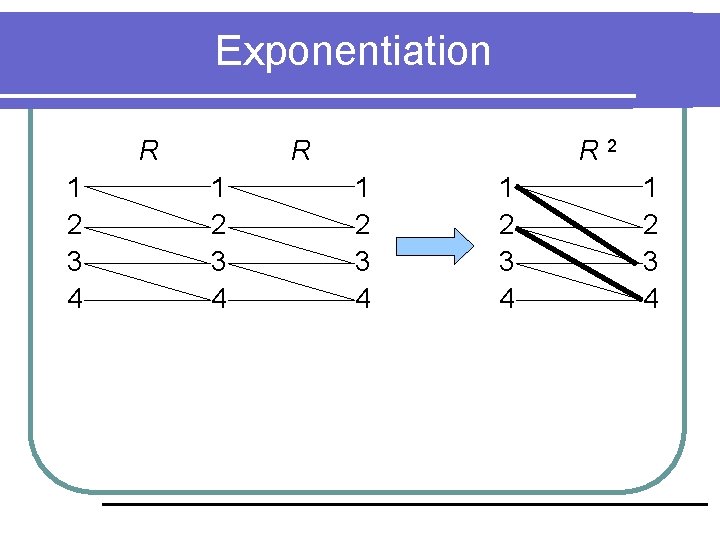
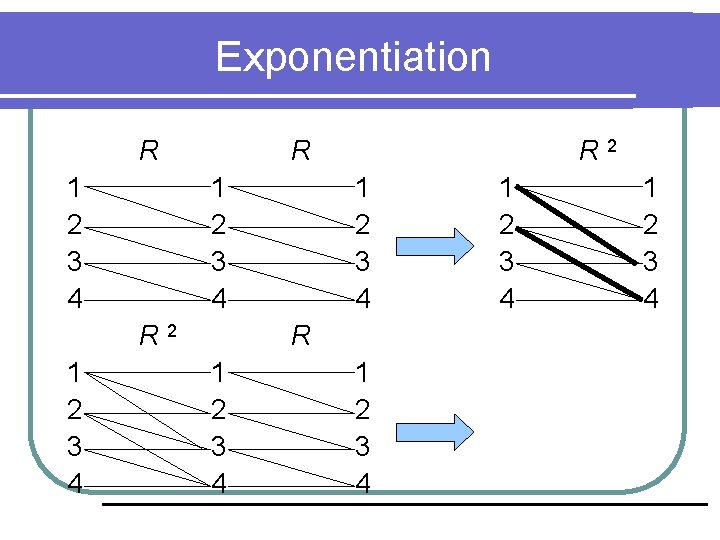
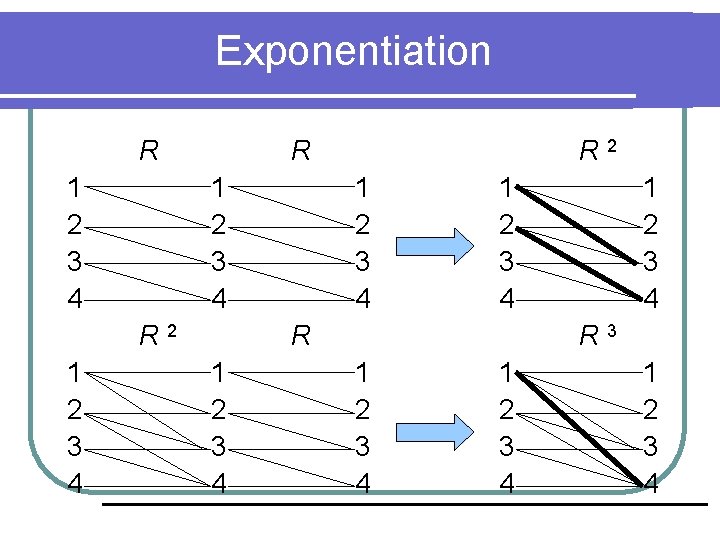
Exponentiation l Une relation R sur A peut être composée avec elle-même, donc exponentiable: DÉF: l Trouvons 1 2 3 4 R 3 si R est donnée par:

Exponentiation R 1 2 3 4

Exponentiation R 1 2 3 4 R 2 1 2 3 4

Exponentiation R 1 2 3 4 R 2 1 2 3 4 R 1 2 3 4

Exponentiation R 1 2 3 4 R 2 1 2 3 4 R 1 2 3 4 R 3 1 2 3 4

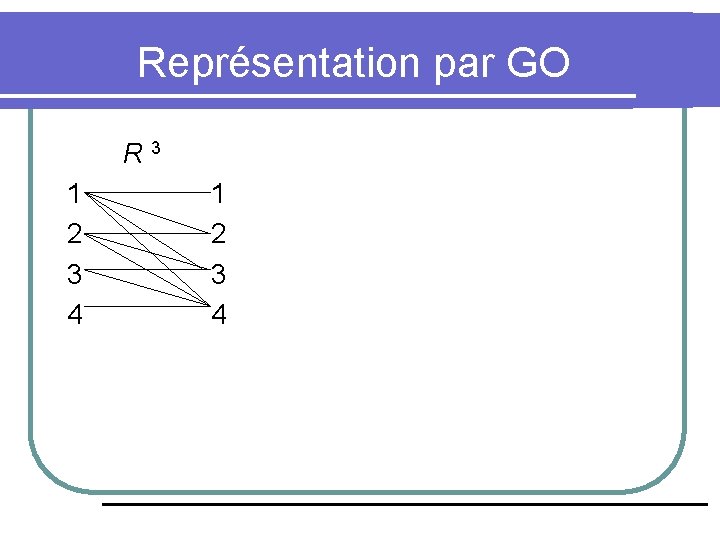
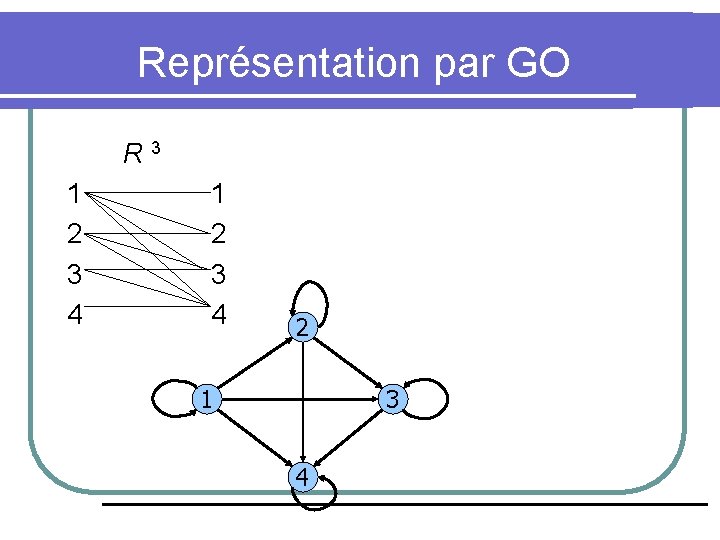
Représentation par Graphe Orienté l Une autre façon de représenter une relation R sur A est avec un graphe orienté (GO) (“directed graph”). L’ensemble A est représenté par des noeuds (ou sommets) et quand une ralation a. Rb est créée, un lien orienté (ou flèche) a b est créé. Des loupes représentent a. Ra. l Représentons la relation R 3 par un GO.

Représentation par GO R 3 1 2 3 4

Représentation par GO R 3 1 2 3 4 2 1 3 4

Application: BD Relationnelle l Les BD Relationnelles permettent d’organiser la structure de larges BDs Design plus simple l Fonctionnalités puissantes l Permet l’utilisation d’algorithmes de recherche efficients l l Les BDs ne sont pas toutes relationnelles Anciens systèmes de BD l XML – structure de données sous forme d’arborescence l

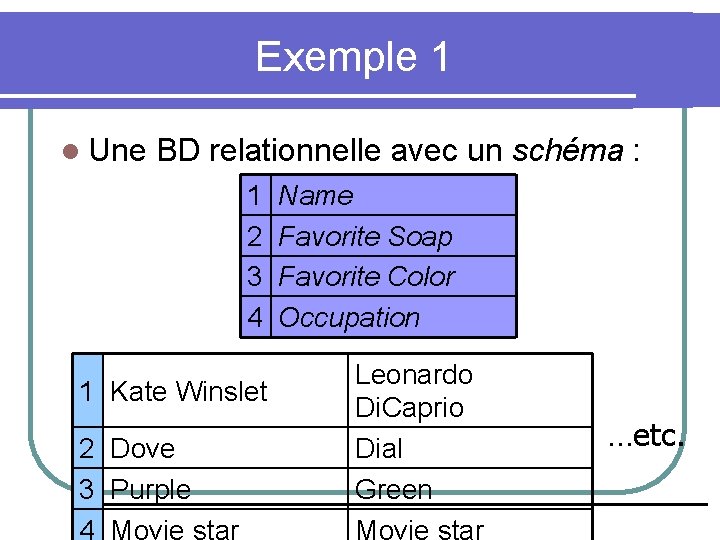
Exemple 1 l Une BD relationnelle avec un schéma : 1 2 3 4 1 Kate Winslet 2 Dove 3 Purple 4 Movie star Name Favorite Soap Favorite Color Occupation Leonardo Di. Caprio Dial Green Movie star …etc.

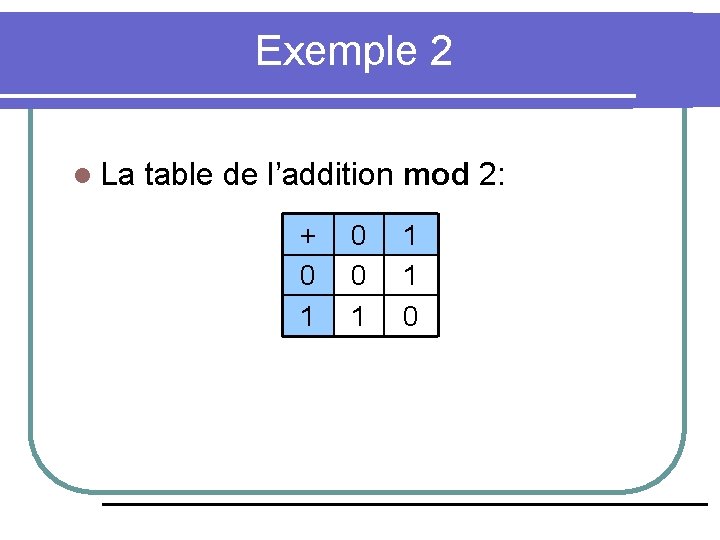
Exemple 2 l La table de l’addition mod 2: + 0 1 0 0 1 1 1 0

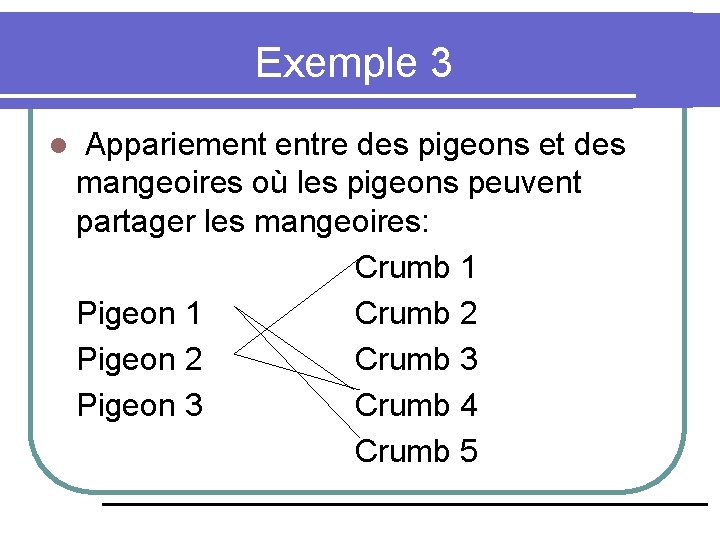
Exemple 3 l Appariement entre des pigeons et des mangeoires où les pigeons peuvent partager les mangeoires: Crumb 1 Pigeon 1 Crumb 2 Pigeon 2 Crumb 3 Pigeon 3 Crumb 4 Crumb 5

Relations: Représentées comme des sousensembles de produits Cartésiens Exemples: 1) BD {Names}×{Soaps}×{Colors}×{Jobs} 2) addition mod 2 {0, 1}×{0, 1} 3) Pigeon-Crumb {pigeons}×{crumbs} 4) Liens de descendances {people}×{people} l

Relations: Représentées comme des sous -ensembles de produits Cartésiens l Quel est le sous-ensemble de l’addition mod 2 ? l Ce sous-ensemble est: { (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0) }

Opérations sur des BD l Plusieurs opérations découlant de la notion de relation sont utiles en BD, comme par exemples: Jointure (join): une généralisation de l’intersection et du produit Cartésien. l Projection: restreindre le nombre de coordonnées. l

Jointure (join) l La jointure de deux relations R, S est la combination de relations en reliant les derniers types (éléments, attributs) de R et les premiers types de S (supposant que ces types sont les mêmes). l Le résultat est une relation avec les types particuliers de S les types communs de S et R et les types particuliers de R.

Jointure (join) Ex: Supposons R est l’addition mod 2 et S est la multiplication mod 2: R = { (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0) } S = { (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 1) } l Dans un cas 2 -join nous joignons les éléments de R et S dont les 2 dernières coordonnées de R et les 2 premières de S sont égales, nous pouvons joindre ces coordonnées et garder les informations de R et S. Par exemple: l (0, 1, 1) (1, 1, 1) 2 -join (0, 1, 1, 1)

Jointure (join) R = { (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0) } S = { (0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 1) } l Avec la notation J 2(R, S) pour la 2 -join. J 2(R, S) = { (0, 0, 0, 0), (0, 1, 1, 1), (1, 0, 1, 0), (1, 1, 0, 0) } l Pour des relations R, S, quelconque? 1) J 0(R, S) => produit Cartésien 2) Jn(R, S) pour n le nombre de coordonnées de R et S => est l’intersection quand n est le nombre de coordonnées

Jointure (join) l Exemple de inner join en langage sql SELECT suppliers. supplier_id, suppliers. supplier_name, orders. order_date FROM suppliers, orders WHERE suppliers. supplier_id = orders. supplier_id; orders suppliers résultats

Jointure (join) l Exemple de outer join en langage sql SELECT suppliers. supplier_id, suppliers. supplier_name, orders. order_date FROM suppliers, orders WHERE suppliers. supplier_id = orders. supplier_id(+); orders suppliers résultats

Projection l La projection est une opération qui permet d’ignorer certaines coordonnées. l Considérons encore R: R = { (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0) } l En projetant les 1 ière et 3 ième coordonnées, nous ignorons la 2 ième coordonnée. nous générons un élément de la projection 1, 3: (0, 1, 1) 1, 3 projection (0, 1)

Projection R = { (0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0) } l Utilisation la notation P 1, 3(R) pour une projection 1, 3. P 1, 3(R) = { (0, 0), (0, 1), (1, 0) }