MATHMATIQUES DISCRTES Chapitre 2 section 4 Franois Meunier

MATHÉMATIQUES DISCRÈTES Chapitre 2 (section 4) François Meunier DMI

Entiers et Algorithmes l Sujets: Algorithme d’Euclide pour trouver le PGCD. l Représentations des entiers en base b. l Binaire, hexadécimal, octal. l Représentation complément-2 des nombres binaires négatifs. l l Algorithmes de l’arithmétique des ordinateurs: l Addition, multiplication et division binaire.

Algorithme d’Euclide pour trouver le PGCD Trouver le pgcd de deux nombres en comparant les facteurs premiers peut être difficile si ces facteurs premiers sont inconnus. l Euclide a démontré que pour toutes paires d’entiers a, b, pgcd(a, b) = pgcd((a mod b), b). l Pour une paire ordonnée a, b telle que a>b, en supposant que b>1 alors (a mod b) < a. l Ceci facilite la recherche du pgcd. l

Exemples l pgcd(372, 164) = pgcd(372 mod 164, 164). l 372 mod 164 = 372 164 372/164 = 372 164· 2 = 372 328 = 44. l pgcd(164, 44) = pgcd(164 mod 44, 44). l 164 mod 44 = 164 44 164/44 = 164 44· 3 = 164 132 = 32. l pgcd(44, 32) = pgcd(44 mod 32, 32) = pgcd(12, 32) = pgcd(32 mod 12, 12) = pgcd(8, 12) = pgcd(12 mod 8, 8) = pgcd(4, 8) = pgcd(8 mod 4, 4) = pgcd(0, 4) = 4.

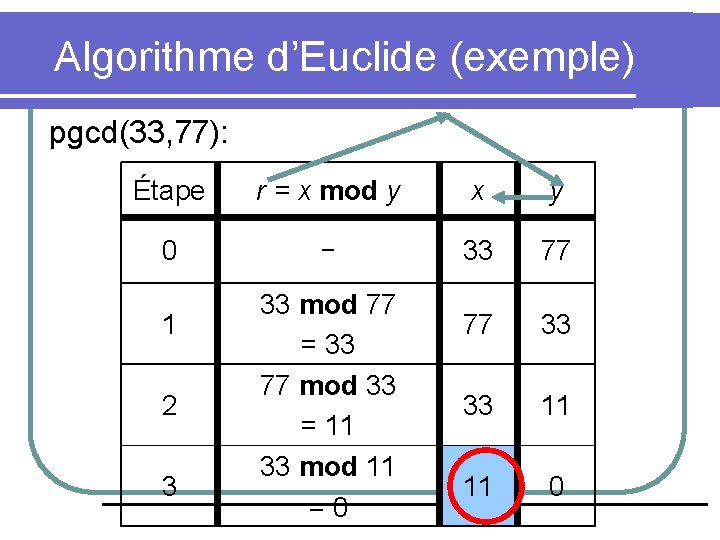
Algorithme d’Euclide (exemple) pgcd(33, 77): Étape r = x mod y x y 0 - 33 77 77 33 33 11 11 0 1 2 3 33 mod 77 = 33 77 mod 33 = 11 33 mod 11 =0

Algorithme d’Euclide (exemple) pgcd(244, 117): Étape r = x mod y x y 0 - 244 117 10 10 7 3 1 1 2 3 4 244 mod 117 = 10 117 mod 10 = 7 10 mod 7 = 3 7 mod 3 = 1 5 3 mod 1=0 1 0 Par définition 244 et 117 sont premiers relatifs.

Algorithme d’Euclide procédure pgcd(a, b: entiers positifs ) tant que b 0 faire r ≔ a mod b; a ≔ b; b ≔ r; Fin retourner a // dernier reste non nul

Systèmes de numération Base-b La représentation de nombres en base-10, utilise les symboles 0 -9. l Mais il n’existe pas seulement la base-10 Toute base b>1 peut être utilisée. l Pour n’importe quels entiers positifs n, b, il existe une séquence de chiffres ak ak-1… a 1 a 0 tels que ai<b et donnant: l Expension en base-b de n

Bases importantes l Base Utiliser seulement parce que nous avons 10 doigts b=10 (décimal): 10 symboles: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Représentation interne des données l Base b=2 (binaire): dans un ordinateur 2 symboles: 0, 1. (“Bits”=“binary digits. ”) Chaque chiffre octal l Base b=8 (octal): correspond à 3 bits 8 symboles: 0, 1, 2, 3, 4, 5, 6, 7. l Base b=16 (hexadécimal): Chiffre HEX correspond à 4 bits 16 symboles: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 10, 11, 12, 13, 14, 15

Convertion dans la Base b Algorithme informel: l Pour convertir un nombre n dans une base b>1: l La valeur du chiffre le moins significatif, calculée par n mod b. l Remplacer n par le quotient n/b. l Répéter les 2 étapes précédentes pour trouver les autres chiffres, TTQ n != 0.

Addition des entiers base-b l Les nombres sont additionnés à partir du chiffre le moins significatif vers le plus significatif en faisant suivre les retenus: base-10 retenu: 1 1 1 7 4 6 3 + 2 9 0 9 1 0 3 7 2 x +y 1 base-16 A 4 F 0 + C B 0 9 1 6 F F 9

Addition des entiers base-b procédure addition(an− 1…a 0, bn− 1…b 0: entiers positifs dans une base a, b) c : = 0 pour j : = 0 à n− 1 {pour chaque chiffre} Sum : = aj+bj+c {somme de 2 -chiffres} sj : = Sum mod base {chiffre bas de la somme } c : = Sum / base {chiffre haut de la somme} fin sn : = c retourner sn…s 0: entier s en base

Addition des entiers binaires procédure addition(an− 1…a 0, bn− 1…b 0: représentations binaires des entiers positifs a, b) c : = 0 pour j : = 0 à n− 1 {pour chaque bit} bit. Sum : = aj+bj+c {somme de 2 -bits} sj : = bit. Sum mod 2 {bit bas de la somme } c : = bit. Sum / 2 {bit haut de la somme} fin sn : = c retourner sn…s 0: entier s en binaire

Multiplication des entiers binaires (+) l La multiplication est simplifiée en binaire puisqu’une X par 2 k correspond à faire un décalage à gauche de kpositions (<<k), et X par 0· 2 k ou 1· 2 k. x y 1·(x<<0) 0·(x<<1) 0·(x<<2) 1·(x<<3) : 1 1 0 0 1 0 1 1 1 0 0 0 0 1 0 1 1

Multiplication des entiers binaires (+) procédure multiplication( xk xk-1…x 1 x 0, yk yk 1…y 1 y 0: entiers binaires positifs) multiplicande x : = xk xk-1…x 1 x 0 multiplicateur p : = 0 // produit partiel pour i : = 0 à k-1 faire si yi == 1 alors p = addition(p , x << i ) retourner p

Complément-2 Élimine le problème de double représentation du 0 l Addition de termes signés est facile l Permet d’utiliser que des opérations d’addition l Représentation de nombres dans l’intervalle -2(k-1) x < 2(k-1) l l Ex: Java: byte [-128 to +127]

Complément-2 l Représentation des négatifs: 1. 2. l l Calculer du complément 1 Additionner 1 Équivalent: -x = ¬x + 1. 00010010 représente 18 11101101 + 1 = 1110 représente -18 Quel est l’intervalle des valeurs entières signées de type int en Java, C ou C++? l Int: 32 -bits: l l Plus grand int=011111…. 1 = 231 -1 = 2, 147, 483, 647 Plus petit int =100000…. 0 = -231 = -2, 147, 483, 648

Addition Complément-2 l. Addition comme celle décrite précédemment 1110 = (-18)10, 11110100 = (-12)10 Additionnés ensemble: (11100010) = (-30)10: retenu: x +y 1 1 1 1 0 1 1 0 1 Le complément-2 de -30 devrait donner 30: (¬ 11100010+1) = (00011101+1) = 00011110. 0 0 0