MATHMATIQUES DISCRTES Chapitre 1 Sections 1 2 Franois















































![Preuve de tautologie [¬p (p q )] q [(¬p p) (¬p q)] q Distributivité Preuve de tautologie [¬p (p q )] q [(¬p p) (¬p q)] q Distributivité](https://slidetodoc.com/presentation_image_h/8bcc587a1b6dd926095349330c3abad7/image-54.jpg)



- Slides: 57

MATHÉMATIQUES DISCRÈTES Chapitre 1 (Sections 1, 2) François Meunier DMI

Organisation du cours l Professeur: François Meunier Bureau: 3081 R Téléphone: 819 376 5011 ext. 3833 Addresse e-mail: Francois. Meunier@uqtr. ca

Livre de référence l Mathématiques Discrètes, K. H. Rosen, Édition Révisée, Traduction de la 3 ième Édition, Chenelière Mc. Graw-Hill. Horaire du cours: Jeudi 8 h 30 -11: 45 3096 R l Site ftp (notes de cours): ftp. uqtr. ca/pub/dmat/meunier/pif 1005 l

Évaluation l 2 travaux pratiques (15% chacun): 30% l 1 examen Intra: 35% l 1 examen Final: 35%

Politique générale des examens l Les examens sont à livres ouverts. l Les examens sont axés sur la compréhension plutôt que sur la mémorisation.

Pourquoi dire math. DISCRÈTES? Que représente des structures discrètes? l “Discrète” – Signifie composées de parties distinctes, séparables. (À l’opposition de continues) discret VS continu digital VS analogique l “Structures” – Objets construits à partir d’objets plus simples selon certains patterns définis. l “Mathématiques Discrètes” – Vouée à l’étude des objets mathématiques et des structures discrètes.

Quelques Structures Discrètes l l l l l Propositions Prédicats Preuves Ensembles Fonctions Ordre Algorithmes Entiers Sommations l l l l l Séquences Chaînes Permutations Combinaisons Relations Graphes Arbres Circuits Logiques Automate

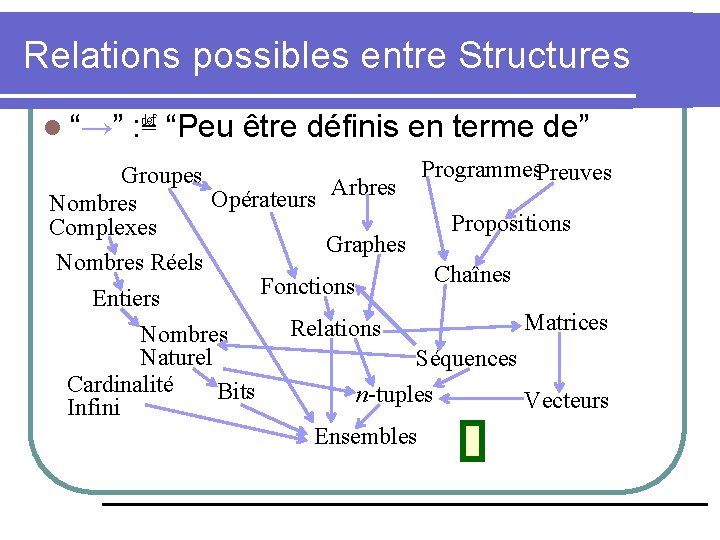
Relations possibles entre Structures l “→” : ≝ “Peu être définis en terme de” Programmes. Preuves Groupes Arbres Opérateurs Nombres Propositions Complexes Graphes Nombres Réels Chaînes Fonctions Entiers Matrices Relations Nombres Naturel Séquences Cardinalité Bits n-tuples Vecteurs Infini Ensembles

Quelques notations utiles

Pourquoi étudier les Math. Discrètes? La base de tout traitement de l’information en format digital: Manipulations discrètes de structures discrètes représentées en mémoire. l Le langage de base et la fondation conceptuelle des sciences informatiques. l Les concepts des Math. Discrètes sont aussi utilisés en mathématique en général, en science, en ingénierie, en économie, biologie, etc. , … l Un outil essentiel pour le raisonnement rationnel. l

Utilisation des Math Discrètes en informatique l l l Algorithmique et structures de données Langage de Programmation Compilateurs et interpréteurs. Réseautique Systèmes d’exploitation Architecture des ordinateurs Systèmes de gestion de base de données l Cryptographie l Correction d’erreurs dans le code l Algorithmes en Graphisme et Animation, engins de jeux, etc. … l

Objectifs du cours l l l Vérifier la validité d’énoncés, de fonctions , d’arguments logiques simples (preuves). Vérifier la rectitude d’un algorithme. Création d’instances simples d’arguments logiques valides et d’algorithmes correctes. Comprendre les définitions et les propriétés de diverses structures discrètes. Lire correctement, représenter et analyser diverses structures discrètes utilisant des notations standards.

Contenu du présent document l Étude des notions fondamentales de la logique. l Notions de propositions logiques. l Notions d’équivalences logiques.

Fondements de la logique La Logique Mathématique permet la manipulation d’énoncés composés élaborés. Incluant: l Un langage formel pour les exprimer. l Une notation concise pour les exprimer. l Une méthodologie pour raisonner de façon objective sur leur véracité ou leur fausseté.

Fondements de la logique: Survol l Logique propositionnelle: Définitions de bases. l Règles d’équivalence et dérivations. l l Logique des prédicats. l Prédicats: Expressions quantifiées de prédicats. l Équivalences et dérivations. l

Logique propositionnelle (section 1. 1) La Logique Propositionnelle est la logique d’énoncés composés construits à partir d’énoncés plus simples en utilisant des opérateurs (connecteurs) Booléens. Quelques applications en science informatique: l Design de circuits electroniques digitaux. l Exprimer des conditions dans des programmes. l Requêtes dans une BD et des engins de recherche.

Définition: Proposition Définition: Une proposition (dénotée p, q, r, …) est: l Un énoncé (i. e. , une phrase déclarative) l avec une sens bien défini, (sans ambiguïté) l Ayant une valeur de vérité soit vraie (T) ou fausse (F) l Jamais les deux, ni entre les deux. l Cependant, il est possible de ne pas connaître la valeur de vérité, l et, la valeur de vérité peut dépendre d’une situation particulière ou du contexte. l Nous verrons plus tard, en étudiant la théorie probabiliste qu’il est possible d’assigner un degré de certitude (entre T ou F) à des propositions. l Pour l’instant pensez! VRAI/FAUX

Exemples de propositions “C’est nuageux. ” (Dans une situation donnée. ) l “Ottawa est la capitale du Canada. ” l “ 1 + 2 = 3” l Exemples qui ne sont pas des propositions: l “Quelle heure est-il? ” (interrogation, question) l “OH ! OH!. ” (sans signification) l “Fait ce devoir !” (impératif, commande) l “Roule 4 -5 minutes, tourne à gauche. . . ” (vague) l “ 1 + 2” (expression sans valeur de vérité)

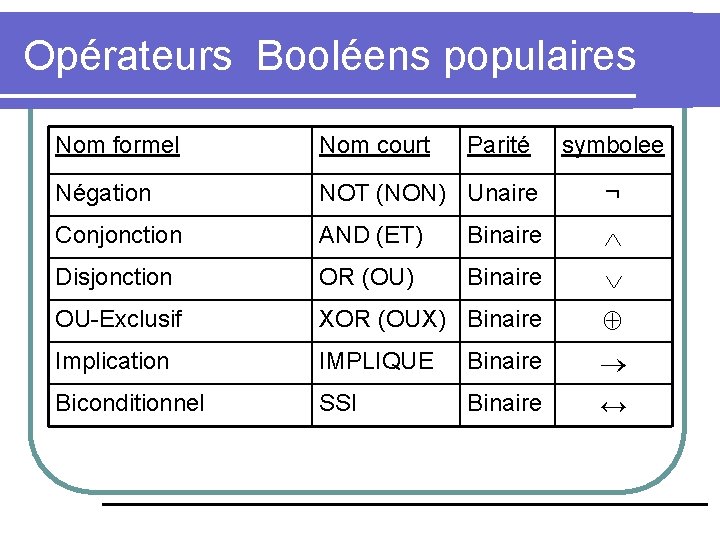
Opérateurs / Connecteurs Un opérateur ou un connecteur combine une ou plusieurs expressions (opérandes) en une expression plus grande, plus élaborée. l Opérateurs Unaires requièrent 1 opérande (ex: − 3); l Opérateurs binaires requièrent 2 opérandes (ex: 3 4). l Opérateurs propositionnels ou Booléens s’appliquent sur des propositions (ou leur valeur de vérité) plutôt que sur des nombres.

Opérateurs Booléens populaires Nom formel Nom court Parité symbolee Négation NOT (NON) Unaire ¬ Conjonction AND (ET) Binaire Disjonction OR (OU) Binaire OU-Exclusif XOR (OUX) Binaire Implication IMPLIQUE Binaire Biconditionnel SSI Binaire ↔

L’opérateur de Négation L’opérateur de négation “¬” (NOT) transforme une prop. dans sa forme logique complémentaire (négation). Ex: SI p = “J’ai les cheveux blanc. ” ALORS ¬p = “Je n’ai pas les cheveux blanc. ” Table de vérité du NOT: T : ≡ True; F : ≡ False “: ≡” “est défini comme” Opérande Résultat

L’opérateur de Conjonction L’opérateur de conjonction “ ” (AND, ET) combine deux propositions pour former ND leur conjonction logique. Ex: p=“J’irai à Québec. ” et q=“J’irai au Châ teau Frontenac. ”, alors p q=“J’ira à Québec et au Château Frontenac. ” Rappel: “ ” pointe vers le haut comme un “A”, et correspond au “ ND”

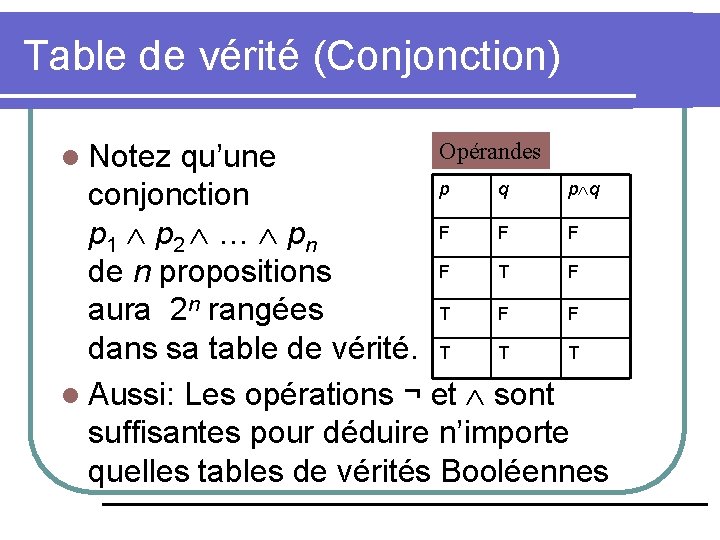
Table de vérité (Conjonction) Opérandes qu’une p q conjonction F F F p 1 p 2 … pn F T F de n propositions T F F aura 2 n rangées dans sa table de vérité. T T T l Aussi: Les opérations ¬ et sont suffisantes pour déduire n’importe quelles tables de vérités Booléennes l Notez

L’opérateur de Disjonction L’opérateur de disjonction “ ” (OU) combine deux propositions pour former une disjonction logique. p=“Mon ordinateur a une bonne carte graphique. ” q=“Mon ordinateur a un CPU performant. ” p q=“Mon ordinateur a soit une bonne carte graphique, or (ou) mon ordinateur a un CPU performant. ”

Table de vérité (Disjonction) l Notez que p q signifie que p est VRAI, ou q est vrai, ou les deux sont vraies! l Cette opération est aussi appelée ou inclusif, et inclus la possibilité que p et q soient VRAIES. Notez la différence avec AND

Un exercise simple Posons p = “Il a plue la nuit dernière”, q = “Le balai mécanique a lavée la rue cette nuit”, r = “La rue est mouillée ce matin. ” Tranduisez chaque proposition: ¬p = “Il n’a pas plue la nuit dernière. ” r ¬p = “La rue est mouillée mais il n’a pas plue” ¬ r p q = “Soit que la rue n’était pas mouillée, ou il a plue la nuit dernière, ou la rue a été lavée cette nuit. ”

L’opérateur OU Exclusif (Exclusive Or) L’opérateur OU-Exclusif “ ” (XOR) combine deux propositions formant leur “OU exclusif” logique. p = “J’obtiendrai un A+ dans ce cours, ” q = “J’abandonnerai ce cours, ” p q = “Je vais soit avoir un A+ dans ce cours, ou j’abandonnerai (mais pas les deux)”

Table de vérité du OU-Exclusif l Notez que p q veut dire que p est vrai, ou q est vrai, mais pas les deux! l Cette opération est appelée OU-exclusif, puisqu’elle exclus la possibilité que p et q soient VRAIES. Notez la différence avec le OR

L’ambiguïté du Language Naturel Notez qu’en français le “ou” peut être ambïgu en regard des cas inclusif et exclusif “Joe est un plombier ou Joe est un politicien. ” - “Joe a eu un A dans son cours de plomberie ou Joe a eu un B dans ce cours. ” Besoin du contexte pour désambiguïser le sens des propositions

L’opération Implication Hypothèse Conclusion L’ implication p q signifie que p implique q. Ex: , posons p = “Vous étudiez beaucoup. ” q = “Vous obtenez une bonne cote. ” p q = “Si vous étudiez beaucoup, vous obtiendrai Alors une bonne cote. ”

La table de vérité de l’Implication q est faux seulement quand p est VRAI mais que q n’est pas VRAI (not true). Le l p q ne veut pas dire seul que p a causé q cas l p q ne requiert pas FAUX que p ou q soit VRAIE l EX: “(1=0) Dumbo l’éléphant vole” est VRAIE lp

Pourquoi l’implication semble bizarre? l Considérons l une phrase comme, “Si je regarde CNN demain, il tombera de la grêle” l En logique, cette phrase est considérée VRAIE tant que je ne regarde pas CNN ou qu’il grêle. l Mais, dans une conversation normale, ce genre d’affirmation est déconcertante et questionnable.

Comment résoudre cette inconsistance l Une phrase en langage courant “SI p ALORS q” peut signifier implicitement: l l l Ce n’est pas le cas en logique. l l “Dans toutes les situations possibles, p implique q. ” SI p est VRAI ALORS q est aussi VRAI. SI p n’est pas VRAI ALORS q est FAUX. Il existe une relation entre, l’hypothèse et la conclusion. p q signifie ¬p V q Ex. : “Si vous avez 100 au final, vous aurez A+” l l l Si vous avez 100, vous attendez à avoir un A+ (1 1=1) Sinon, vous pourriez avoir un A+ quand même (0 1=1) Par contre, si vous avez un 100 et n’avez pas un A+, vous sentirez probablement lésé (1 0 = 0)

Examples d’Implications l “Si ce cours ne se termine jamais, Alors le soleil se lèvera demain. ” True or False? l “Si lundi est un jour de la semaine, Alors Je suis un singe. ” True or False? l “Si 1+1=6, Alors Obama est président. ” True or False? l “Si la Suisse est un fromage, Alors je suis plus riche que Warren Buffet. ” True or False?

Sens de phrases en langage courant p q l l l l “p implique q” “Si p, Alors q” “Si p, q” “quand p, q” “chaque fois que p, q” “q si p” “q quand p” “q chaque fois que p” l l l “p seulement si q” “p est suffisant pour que q” “q est nécessaire pour que p” “q découle de p” “q est supposé par p”

Réciproque, Inverse, Contraposée Formes découlants de l’implication p q: l Sa réciproque est: q p. l Son inverse est: ¬p ¬q. l Sa contraposée: ¬q ¬ p. l Une de ces formes a le même sens (même table de vérité) que p q. Laquelle ?

Comment en être certain? Prouvons l’équivalence de p q et sa contraposée par table de vérité:

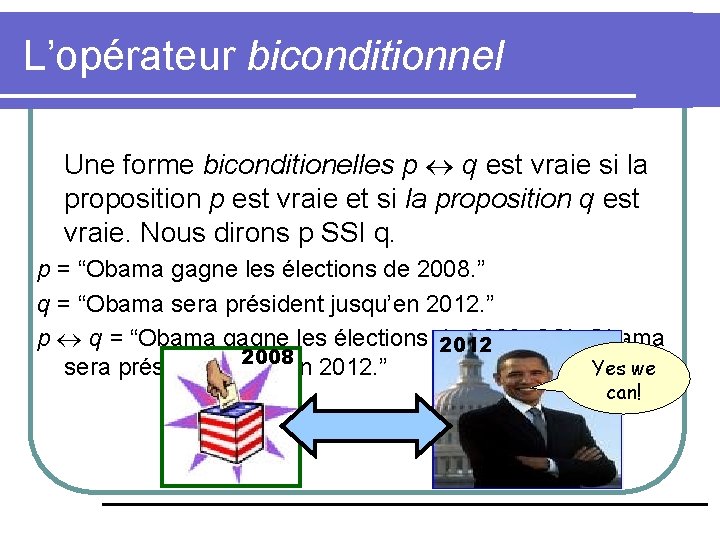
L’opérateur biconditionnel Une forme biconditionelles p q est vraie si la proposition p est vraie et si la proposition q est vraie. Nous dirons p SSI q. p = “Obama gagne les élections de 2008. ” q = “Obama sera président jusqu’en 2012. ” p q = “Obama gagne les élections de 2008, SSI, Obama 2012 2008 sera président jusqu’en 2012. ” Yes we can!

Table de vérité de la biconditionnelle p q signifie que p et q ont la même valeur de vérité. l Notez que cette table de vérité est l’opposée du XOR l Donc, p q est équivalent ¬(p q) l p q ne veut pas dire que p et q sont VRAIES, ou que chacune est la cause de l’autre, ou découlent d’une cause commune.

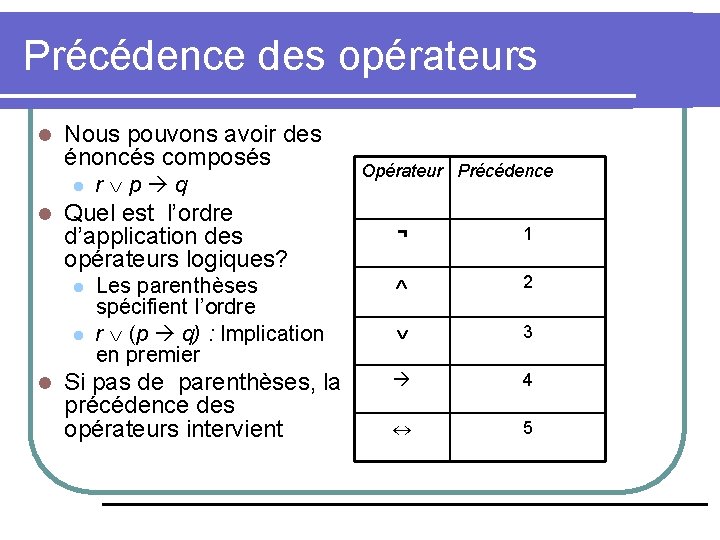
Précédence des opérateurs l Nous pouvons avoir des énoncés composés l l Quel est l’ordre d’application des opérateurs logiques? l l l r p q Les parenthèses spécifient l’ordre r (p q) : Implication en premier Si pas de parenthèses, la précédence des opérateurs intervient Opérateur Précédence ¬ 1 2 3 4 5

Opérations Booléennes (Sommaire) l Table de vérité des opérateurs logiques vus jusqu’à maintenant.

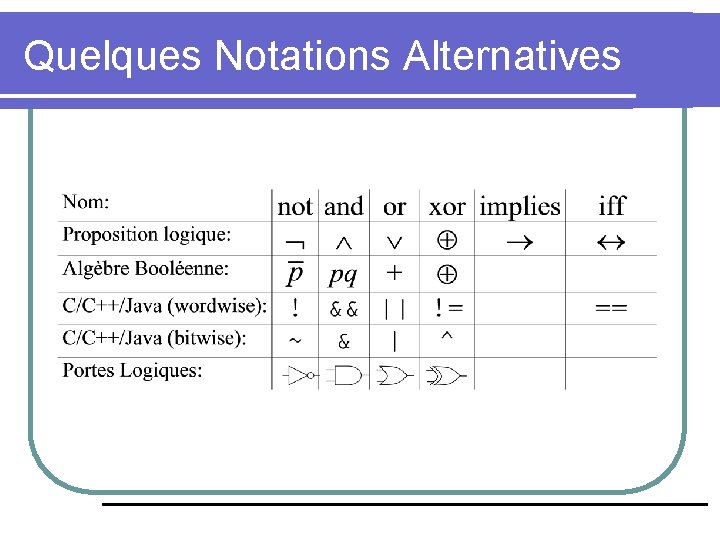
Quelques Notations Alternatives

Opérations Logiques et Binaires Un bit est un binary (base 2) digit: 0 ou 1. l Les bits sont aussi utilisés pour représenter des valeurs de vérité. l Par convention: 0 représente “FAUX”; 1 représente “VRAI”. l L’ Algèbre Booléenne est comme l’algèbre conventionnelle sauf que les variables sont logiques (bits), + est le “or”, et la multiplication est le “and”. l

Chaîne de Bits l Une chaîne de Bits de longueur n est une séquence ordonnée (séries, tuple) de n 0 bits. l Par convention, les chaînes de bits sont écrites généralement de gauche à droite: l BLPS “ 1001101010” est 1. l Alors la chaîne de bits correspond en base 10 à: 11012=8+4+1=13.

Opérations sur les Bits (Bitwise) l Opérations booléennes peuvent être appliquées sur des chaînes de bits autant que des bits individuels. l EX: 0110110110 110001110111111 (Bit-wise OR) 0100010100 (Bit-wise AND) 101011 (Bit-wise XOR)

Récapitulations (sec. 1. 1) Définitions sur les propositions l Opérateurs sur les propositions logiques l l l Notations symboleiques. Équivalents dans le langage courant. Sens logique. Tables de vérité. Proposition simples vs. composées. l Notations alternatives. l Bits et chaînes de bits. l Section: 1. 2 l l l Équivalences propositionnelles. Comment les prouver.

Équivalence Propositionnelle (sec. 1. 2) l Deux propositions composées syntaxiquement différentes peuvent être identiques du point de vue sémantique. Elles sont alors dites équivalentes. Il existe: Diverses règles ou lois d’équivalence. l Des dérivations symboliques pour prouver les équivalences. l

Tautologies et Contradictions Une tautologie est une proposition composée qui est VRAIE et ce pour toutes les combinaisons de valeurs des propositions atomiques la composant. Ex. p p [Quelle est la table de vérité? ] Une contradiction est une proposition composée qui est FAUSSE dans tous les cas. Ex. p p [La table de vérité? ] Les autres propositions composées sont des contingences.

Équivalence logique p q l Les propositions composées p et q sont logiquement équivalentes (exprimée p q) SSI p et q possèdent les mêmes valeurs logiques dans toutes les rangées de leur table de vérité.

Preuve d’équivalence par table de vérité Ex. Prouvez que p q ( p q). F T T T F F T T T

Lois d’Équivalence l Similaires aux identités arithmétiques utilisées en algèbre, mais appliquées aux équivalences propositionnelles. l Peuvent être substituées entièrement ou en partie à des propositions complexes pour en prouver l’équivalence.

Lois d’équivalence- Exemples p T p p F p l Domination: p T T p F F l Idempotence: p p p l Double négation: p p l Commutativité: p q q p l Associativité: (p q) r p (q r) l Identité:

Autres lois d’équivalence l Distributivité: p (q r) (p q) (p r) De Morgan: (p q) p q l Tautologie/contradiction triviale (Équivalences logiques utiles: ELU) p p T p p F (p q) ( p q) l
![Preuve de tautologie p p q q p p p q q Distributivité Preuve de tautologie [¬p (p q )] q [(¬p p) (¬p q)] q Distributivité](https://slidetodoc.com/presentation_image_h/8bcc587a1b6dd926095349330c3abad7/image-54.jpg)
Preuve de tautologie [¬p (p q )] q [(¬p p) (¬p q)] q Distributivité [ F (¬p q)] q [¬p q ] q ELU Identitité ¬ [¬p q ] q ELU [¬(¬p) ¬q ] q De. Morgan [p ¬q ] q Double Négation p [¬q q ] Associativité p [q ¬q ] p T T Commutativité ELU Domination

Autre preuve d’équivalence logique ¬(p (¬p q )) (¬p ¬q) ¬p ¬(¬p q ) De Morgan ¬p [¬(¬p) ¬q )] De Morgan ¬p (p ¬q ) Double Négation (¬p p) (¬p ¬q) Distributivité F (¬p ¬q) ELU (¬p ¬q) F (¬p ¬q) Commutativité Identité

Définir des opérateurs par les Équivalences Avec les équivalences, de nouveaux opérateurs peuvent être déduits en termes d’autres opérateurs: l OU Exclusif: p q (p q) (q p) l Implication: p q p q l Biconditionnelle: p q (p q) (q p) p q (p q)

Revue: Logique Propositionnelle sec. (1. 11. 2) l Propositions atomiques : p, q, r, … l Opérateurs Booléens : l Propositions composées: s : (p q) r l Équivalences: p q (p q) l Preuves d’équivalences par: Tables de vérité. l Dérivations symboliques. p q r … l
 Mathmatiques
Mathmatiques Mathmatiques
Mathmatiques Résumé chapitre par chapitre tirez pas sur le scarabée
Résumé chapitre par chapitre tirez pas sur le scarabée Le petit prince chapitre 1
Le petit prince chapitre 1 Le petit prince résumé chapitre par chapitre
Le petit prince résumé chapitre par chapitre Lecture analytique petit pays chapitre 30
Lecture analytique petit pays chapitre 30 Franois villon
Franois villon Pic franois
Pic franois Franois villon
Franois villon Maria chapdelaine résumé par chapitre
Maria chapdelaine résumé par chapitre Le dernier jour d'un condamné situation des passages
Le dernier jour d'un condamné situation des passages Le petit prince chapitre 14
Le petit prince chapitre 14 Le monde du travail chapitre 2 answers
Le monde du travail chapitre 2 answers Les quartiles en statistique
Les quartiles en statistique Qualiroute chapitre g
Qualiroute chapitre g Jean chapitre 11
Jean chapitre 11 La petite fille au kimono rouge lecture suivie
La petite fille au kimono rouge lecture suivie The pronoun y chapitre 3
The pronoun y chapitre 3 Grammaire 1 chapitre 5
Grammaire 1 chapitre 5 1 pierre chapitre 5
1 pierre chapitre 5 Jean chapitre 5
Jean chapitre 5 Chapitre 2 vocabulaire 1
Chapitre 2 vocabulaire 1 Thème introductif la périodisation
Thème introductif la périodisation Chapitre 2 richesse et pauvreté dans le monde
Chapitre 2 richesse et pauvreté dans le monde Le petit prince et le buveur
Le petit prince et le buveur Chapitre 14 cinquieme rencontre
Chapitre 14 cinquieme rencontre Le petit prince chapitre 6
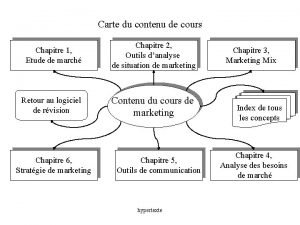
Le petit prince chapitre 6 Etude de marché
Etude de marché Le petit prince chapitre 13
Le petit prince chapitre 13 Jean chapitre 9
Jean chapitre 9 Matthieu chapitre 26
Matthieu chapitre 26 Chapitre 7 vocabulaire 1 french 2
Chapitre 7 vocabulaire 1 french 2 Jean chapitre 6
Jean chapitre 6 Registre tragique dans le dernier jour d'un condamné
Registre tragique dans le dernier jour d'un condamné Daniel 12 1 4
Daniel 12 1 4 Grammaire 1
Grammaire 1 Chapitre fonction seconde
Chapitre fonction seconde Blanche canaby
Blanche canaby Lieux de fabrication des objets techniques
Lieux de fabrication des objets techniques Chapitre 7 observatoire
Chapitre 7 observatoire Nehemie chapitre 1
Nehemie chapitre 1 Chapitre 49 dernier jour d'un condamné
Chapitre 49 dernier jour d'un condamné Marc chapitre 14
Marc chapitre 14 Matthieu chapitre 3
Matthieu chapitre 3 Ainsi parle le saigneur characters
Ainsi parle le saigneur characters Tite chapitre 2
Tite chapitre 2 Allons en ville chapitre 9 vocabulaire 1
Allons en ville chapitre 9 vocabulaire 1 Route de chlifa résumé
Route de chlifa résumé Chapitre 26 le dernier jour d'un condamné analyse
Chapitre 26 le dernier jour d'un condamné analyse Daniel chapitre 11
Daniel chapitre 11 Daniel chapitre 1
Daniel chapitre 1 Le petit prince chapitre 7
Le petit prince chapitre 7 Chapitre 7 vocabulaire 1
Chapitre 7 vocabulaire 1 Chapitre 7 évaluer le risque client
Chapitre 7 évaluer le risque client Jean chapitre 4
Jean chapitre 4 Bilan thermique du corps humain schema
Bilan thermique du corps humain schema Le faucon déniché questionnaire
Le faucon déniché questionnaire Chapitre 3 l'énergie et ses manifestations
Chapitre 3 l'énergie et ses manifestations