MATEMTICA DISCRETA Y LGICA 2 Prof FERNANDO GERFAUO

MATEMÁTICA DISCRETA Y LÓGICA 2 Prof. : FERNANDO GERFAUO. TECNÓLOGO EN INFORMÁTICA. Sede: PAYSANDÚ. AÑO 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. TEMARIO- BIBLIOGRAFÍA Conceptos básicos de la Teoría de Grafos • Definiciones • Subgrafo, complementos, isomorfismo • Grado de un vértice, circuitos y recorridos Eulerianos • Ciclos y caminos Hamiltonianos • Árboles Lógica de predicados • Cuantificadores • Estructuras • Semántica básica • Propiedades básicas de la Lógica de Predicados Bibliografía: • Logic and Structure. Dirk van Dalen. Ed. Springer-Verlag. • Matemáticas Discreta y Combinatoria. Ralph P. Grimaldi. Ed. Addison Wesley Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES ABIERTAS Proposiciones abiertas: Una frase declarativa es una proposición abierta si: 1) contiene una o más variables, 2) no es una proposición, pero 3) se convierte en una proposición cuando las variables que aparecen en ellas se remplazan por ciertas opciones permisibles. Observación: Las opciones permisibles forman lo que se llama el dominio o universo de discurso para la proposición abierta. El universo comprende las opciones que se quieren considerar o permitir para la variable o variables de la proposición abierta. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES ABIERTAS Ejemplos y notaciones: La frase “x+5 es un entero par” no es necesariamente verdadera o falsa, salvo que se conozca el valor que remplazará a la variable x. Si se restringe la elección de la variable al conjunto de los números enteros, entonces la frase “x+5 es un entero par” resulta una proposición abierta con universo de discurso ℤ. La proposición abierta “x+5 es un entero par” se puede denotar con p(x) (o q(x) o r(x), etc. ). Entonces ¬p(x) se puede leer como “x+5 no es un entero par”. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES ABIERTAS Ejemplos y notaciones: Sea q(x, y) la proposición abierta “x+5, y-x y 3 x+y son enteros pares” con universo de discurso ℤ. En este ejemplo, cada una de las variables aparece más de una vez. Se sobreentiende que cuando se remplaza una de las letras x por un entero particular, se debe remplazar la otra letra x por el mismo valor. De la misma forma, cuando se sustituye y por un entero dado, se debe realizar la misma sustitución para todas las apariciones de la variable y. ¿Cuáles son los valores de verdad de p(-1), ¬p(3), q(5, -3) y q(-4, 2)? ¿Cómo se lee ¬q(x, y)? ¿Cuál es el valor de verdad de ¬q(5, -3)? ¿Y de ¬q(-4, 2)? Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES ABIERTAS A partir de los ejemplos anteriores, se ve que para ambas expresiones p(x) y q(x, y), algunas sustituciones generan proposiciones verdaderas y otras generan proposiciones falsas. Por lo tanto, se pueden construir las siguientes proposiciones verdaderas: “Existe algún x, tal que x+5 es un entero par”, o “para algún x, p(x)”. “Para algunos x, y se cumple que x+5, y-x y 3 x+y son enteros pares”, o “para algunos x, y, q(x, y)”. Las frases “para algún x” y “para algunos x, y”, cuantifican las proposiciones abiertas p(x) y q(x, y), respectivamente. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. CUANTIFICADORES El cuantificador existencial. La proposición “para algún x, p(x)” utiliza el cuantificador existencial “para algún x”, que también se puede expresar como “para al menos un x” o “existe un x tal que”. Notación: En forma simbólica, este cuantificador se representa como ∃x. La proposición “para algún x, p(x)” se expresa, en forma simbólica, como: ∃x p(x). La proposición “para algunos x, y, q(x, y)” se escribe como ∃x ∃y q(x, y). En este caso, se puede utilizar la notación ∃x, y para abreviar ∃x ∃y, de modo que la proposición ∃x ∃y q(x, y) queda ∃x, y q(x, y). Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. CUANTIFICADORES El cuantificador universal de denota con ∀x; se lee “para todo x”, “para cada x” o “para cualquier x”. “Para todo x, y”, “para todos x y y” se denota con ∀x ∀y, que se puede abreviar ∀x, y. Si p(x) es la proposición abierta del ejemplo anterior, entonces la proposición ∀x p(x) es falsa. Si se considera la proposición abierta r(x): 2 x es un entero par, con universo de discurso ℤ, entonces la proposición ∀x r(x) es verdadera. ¿Cuál es el valor de verdad de la proposición ∃x r(x)? ¿Cuáles son los valores de verdad de ∀x ¬r(x) y ∃x ¬r(x)? Prof. : Fernando Gerfauo Año 2019. -

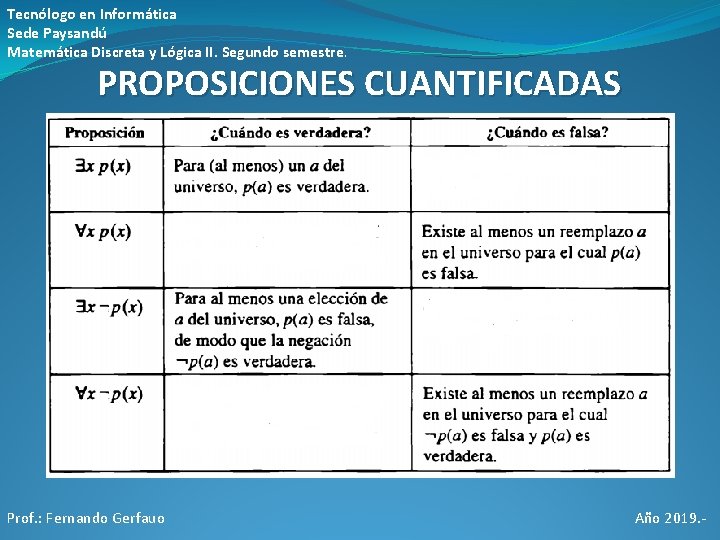
Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES CUANTIFICADAS Prof. : Fernando Gerfauo Año 2019. -

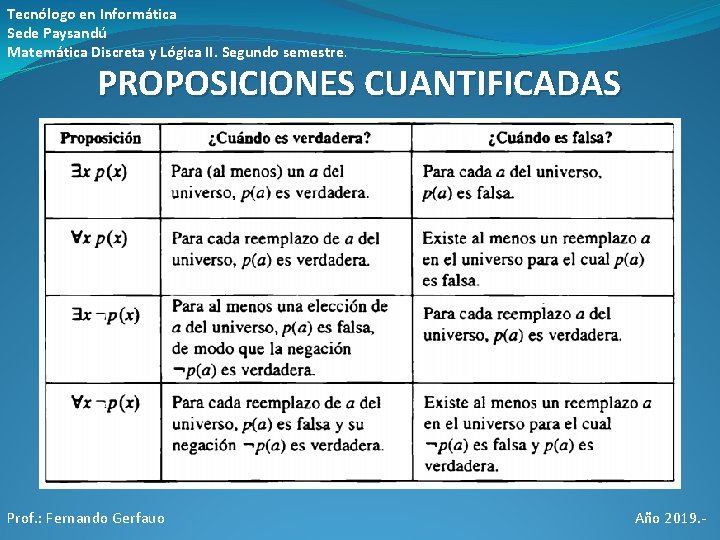
Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. PROPOSICIONES CUANTIFICADAS Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. EQUIVALENCIA LÓGICA-IMPLICACIÓN LÓGICA Proposiciones abiertas lógicamente equivalentes. Sean α(x) y β(x) dos proposiciones abiertas definidas para un universo de discurso dado. Las proposiciones abiertas α(x) y β(x) son (lógicamente) equivalentes cuando la proposición α(a) ↔ β(a) es verdadera para cada reemplazo a del universo dado. Notación: Se escribe ∀x ( α(x) ⇔ β(x) ). Si la implicación α(a) → β(a) es verdadera para cada elemento a del universo, entonces se escribe ∀x ( α(x) ⇒ β(x) ) y se dice que α(x) implica lógicamente β(x). Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. EQUIVALENCIA LÓGICA-IMPLICACIÓN LÓGICA Equivalencias e implicaciones lógicas para proposiciones cuantificadas de una variable. Sean α(x) y β(x) dos proposiciones abiertas definidas para un universo de discurso dado. Se cumple que: ∃x (α(x) ˄ β(x) ) ⇒ ( ∃x α(x) ˄ ∃x β(x) ) ∃x (α(x) ˅ β(x) ) ⇔ ( ∃x α(x) ˅ ∃x β(x) ) ∀x (α(x) ˄ β(x) ) ⇔ (∀x α(x) ˄ ∀x β(x) ) ( ∀x α(x) ˅ ∀x β(x) ) ⇒ ∀x ( α(x) ˅ β(x) ) Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. EQUIVALENCIA LÓGICA-IMPLICACIÓN LÓGICA Reglas para negar proposiciones con un cuantificador. Sea α(x) una proposición abierta definida para un universo dado. Se cumple que: ¬ ( ∃x α(x)) ⇔ ∀x (¬ α(x)) ¬ ( ∀x α(x) ) ⇔ ∃x (¬ α(x)) ¬ ( ∃x (¬ α(x) ) ) ⇔ ∀x (¬( ¬ α(x))) ⇔ ∀x α(x) ¬ ( ∀x ( ¬ α(x) ) ) Prof. : Fernando Gerfauo ⇔ ∃x ( ¬ α(x) )) ⇔ ∃x α(x) Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LÓGICA DE PREDICADOS En Lógica Proposicional (Matemática Discreta y Lógica I), se analizan frases y argumentaciones, descomponiéndolas en frases constituyentes simples, y considerando éstas como piezas de la construcción. No obstante, existen argumentaciones que no son susceptibles de un tratamiento de este tipo. Todos los hombres son mortales Sócrates es un hombre Por lo tanto, Sócrates es mortal. Parece una argumentación válida, pero si se trata de simbolizar su forma, se obtiene: p, q ⊦ r. Pero “ésta no es una forma argumentativa válida”. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LÓGICA DE PREDICADOS La validez en el caso anterior no depende de las relaciones entre las premisas y la conclusión en tanto que enunciados simples, sino de relaciones entre partes de los enunciados que intervienen y entre las formas de éstos. Todos los A son B, C es un A, Por lo tanto C es un B. En castellano, todo enunciado simple tiene un sujeto y un predicado, cada uno de los cuales puede consistir en una sola palabra, una frase breve o toda una cláusula. En forma muy grosera, el sujeto es la cosa acerca de la cual el enunciado está afirmando algo, y el predicado se refiere a una propiedad que posee el sujeto. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LÓGICA DE PREDICADOS Ejemplos: a) Sócrates es un hombre. b) Yo escribo libros. c) El número cuya raíz es -1 no es real. d) El mundo nos debe a todos el sustento. Informalmente, si se simbolizan los predicados con letras mayúsculas (A, B, C, . . . ) y los sujetos mediante letras minúsculas, entonces el enunciado a) del ejemplo anterior, se simboliza del siguiente modo: H(s) simboliza “Sócrates es un hombre”, siendo H una letra de predicado que simboliza “es un hombre” y s simboliza a “Sócrates”. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LÓGICA DE PREDICADOS Ejemplos: a) Sócrates es un hombre y es mortal. b) 5 es un entero mayor que 3 y tiene un factor primo. Los enunciados compuestos también pueden simbolizarse de esta manera, simbolizando todos los enunciados simples que los constituyen. ¿Y cómo se pueden simbolizar estos enunciados? c) d) Todos los hombres son mortales. Todo entero tiene un factor primo. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN La idea es construir un sistema deductivo formal como se hizo en Lógica Proposicional, describiendo en primera instancia un lenguaje formal, dando: 1) el alfabeto de símbolos y 2) las reglas de construcción de las palabras de dicho lenguaje, que se les llamará fórmulas bien formadas. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Alfabeto de símbolos. • a, b, c, … son constantes individuales. • x, y, z, … son variables. • A 1, B 1, C 1, …; A 2, B 2, C 2, …; A 3, B 3, C 3, …; son letras de predicado. • f 1, g 1, h 1, …; f 2, g 2, h 2 , …; f 3, g 3, h 3 , …; son letras de función. • ⊥, ¬, ˄, ˅, →, ↔, son conectivas lógicas. • ∀, ∃ son cuantificadores. • ( , ) y , son signos de puntuación. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Observaciones: Las constantes individuales a, b, c, … se incluyen para que se tengan en el lenguaje fórmulas que puedan interpretarse como enunciados acerca de cosas particulares. Las letras de predicado A 1, B 1, … son letras de predicado monarias que están pensadas para representar predicados monarios (propiedades). Las letras A 2, B 2, … son letras de predicados binarias, necesarias para simbolizar predicados binarios (relaciones). Y así sucesivamente. Si bien una función es una clase especial de relación, las letras de función serán fundamentales en el lenguaje formal. El superíndice que se les asigna indica el número de argumentos. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Ejemplo 1: Si se quiere un lenguaje de primer orden apropiado para enunciados referentes a la aritmética de los números naturales, dicho lenguaje debería contener (junto con las variables, los signos de puntuación, las conectivas y los cuantificadores) los símbolos: a, para representar el 0, A 2, para representar =, f 1, para representar la función “sucesor de” o “siguiente de”, f 2, para representar +, g 2, para representar *. ¿Cómo se interpreta A 2 ( f 2(x, y), g 2 (x, y) )? ¿y (∀x) (¬ A 2 (a, f 1(x)) )? Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Ejemplo 2: Si se quiere un lenguaje de primer orden apropiado para enunciados relativos a grupos, dicho lenguaje puede contener (junto con las variables, los signos de puntuación, las conectivas y los cuantificadores) los símbolos: a, para representar el elemento identidad 1, A 2, para representar =, f 1, para representar la función que transforma cada elemento en su inverso. f 2, para representar la operación binaria del grupo. ¿Cómo se interpreta A 2 ( f 2(x, f 1(x)), a )? Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Antes de definir las fórmulas bien formadas se necesitan algunos conceptos. El conjunto TERM. Sea L un lenguaje de primer orden. Se define inductivamente el lenguaje de los términos de L como sigue: (i) Las variables y las constantes son términos de L. (ii) Si fn es una letra de función de L y t 1, t 2, …, tn son términos de L, entonces fn (t 1, t 2, …, tn) es un término de L. (iii) C. C. Observación: los términos son expresiones del lenguaje formal que se interpretan como objetos. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN Fórmula atómica. Las fórmulas atómicas son las expresiones más sencillas del lenguaje que son interpretables como aseveraciones, como por ejemplo, que un cierto objeto verifica una cierta propiedad. Fórmulas atómicas de L: i) ⊥ es una fórmual atómica de L. ii) Si Ak es una letra de predicado de L y t 1, t 2, …, tk son términos de L, entonces Ak (t 1, t 2, …, tk) es una fórmula atómica de L. Observación: Estas fórmulas se pueden combinar de acuerdo con ciertas reglas lógicas, y ocupan un lugar comparable al de las letras de proposición en PROP. Prof. : Fernando Gerfauo Año 2017. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. LENGUAJES DE PRIMER ORDEN El conjunto FORM. Sea L un lenguaje de primer orden. Se define el conjunto de la fórmulas bien formadas de L en forma inductiva, como sigue: (i) Toda fórmula atómica de L es una fórmula bien formada de L. (ii) Si α y β son fórmulas bien formadas de L, entonces (α˄β), (α˅β), (α→β) y (α↔β) son fórmulas bien formadas de L. (iii) Si α es una fórmula bien formada de L, entonces (¬α) es una fórmula bien formada de L. (iv) Si α es una fórmula bien formada de L y x es una variable cualquiera de L, entonces (∃x)α y (∀x)α son fórmulas bien formadas de L. (v) C. C. Prof. : Fernando Gerfauo Año 2019. -

Tecnólogo en Informática Sede Paysandú Matemática Discreta y Lógica II. Segundo semestre. BIBLIOGRAFÍA CONSULTADA: Año 2019. -