Loglinear Models for Independence and Interaction in Threeway

Loglinear Models for Independence and Interaction in Three-way Tables Veronica Estrada Robert Lagier

Quick Review from Agresti, 4. 3 • Poisson Loglinear Models are based on Poisson distribution of Y counts and employ log link function: log μY = α + βx μY = exp(α + βx)

Value of Loglinear Models? • Used to model cell counts in contingency tables where at least 2 variables are response variables • Specify how expected cell counts depend on levels of categorical variables • Allow for analysis of association and interaction patterns among variables

Models for Two-way Tables • Independence Model – μij = μαi βj – log μij = λ + λi. X + λj. Y – where λi. X is row effect, and λj. Y is column effect – odds for column response independent of row • Saturated (Dependence) Model – terms logμij = λ + λi. X + λj. Y + λij. XY – where λij. XY are association that represent interactions between X and Y – odds for column response depends on row

Loglinear Models for Three-way (I x J x K) Tables • Describe independence and association patterns • Assume a multinomial distribution of cell counts with cell probabilities {πijk} • Also apply to Poisson sampling with means {µijk}

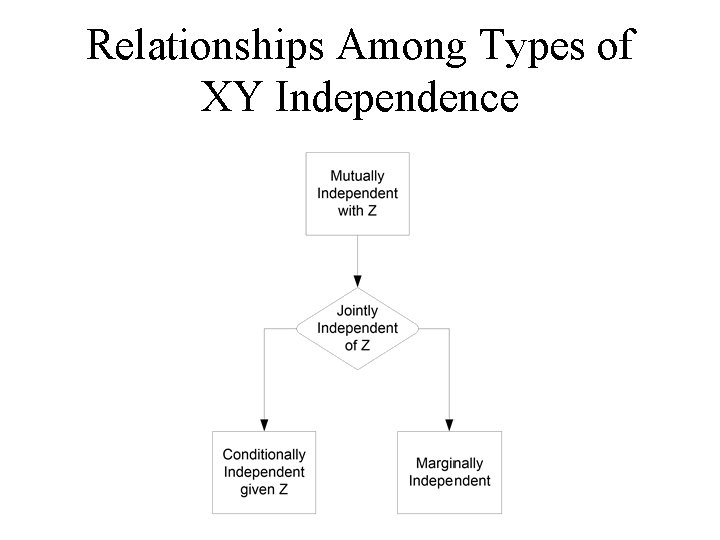
Types of Independence for Cell Probabilities in I x J x K Tables • Mutual Independence • Joint Independence • Conditional Independence • Marginal Independence

Mutual Independence • πijk = (πi++) (π+j+) (π++k) for all i, j, k • Loglinear Model for Expected Frequencies – log μijk = λ + λi. X + λj. Y + λk. Z • Interpretation: – X independent of Y independent of Z independent of X – No association between variables

Joint Independence • X jointly independent of Y and Z: – πijk = (π+jk) (πi++) for all i, j, k • Loglinear Model for Expected Frequencies – log μijk = λ + λi. X + λj. Y + λk. Z + λjk. YZ • Interpretation: – X independent of Y and Z – Partial association between variables Y and Z • 3 Joint Independence Models

Conditional Independence • X and Y conditionally independent of Z: – πijk = (πi+k) (π+jk) / π++k for all i, j, k • Loglinear Model for Expected Frequencies – log μijk = λ + λi. X + λj. Y + λk. Z + λik. XZ + λjk. YZ • Interpretation: – X and Y independent given Z – Partial association between X, Z and Y, Z • 3 Conditional Independence Models

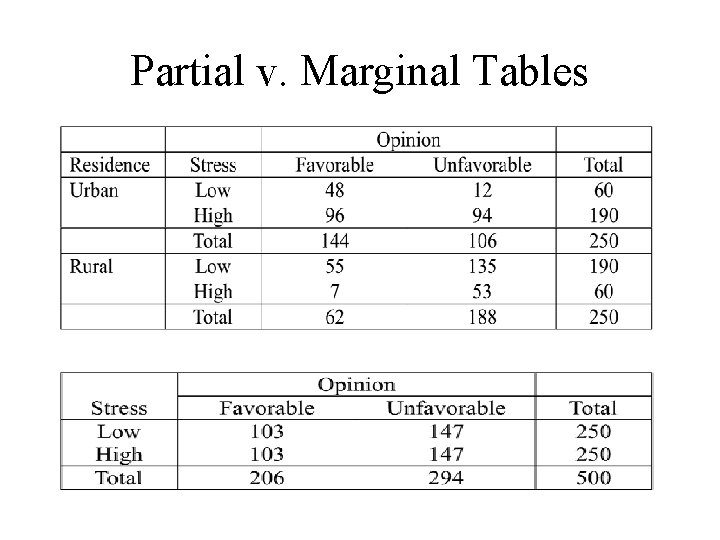
Marginal Independence • X and Y marginally independent of Z: – πij+ = (πj++) (π+j+) for all i, j, k • Interpretation: – X and Y independent in the two-way table that has been collapsed over the levels of Z – Variables may have different strength of marginal association than conditional (partial) association - Simpson’s Paradox

Partial v. Marginal Tables

Relationships Among Types of XY Independence

Homogenous Association Model • Loglinear Model for Expected Frequencies – log μijk = λ + λi. X + λj. Y + λk. Z + λij. XY + λik. XZ + λjk. YZ • Interpretation: – Homogenous association: • identical conditional odds ratios between any two variables over the levels of the third variable • θij(1) = θij(2) = … = θij(K) for all i and j

Saturated Model • Loglinear Model for Expected Frequencies – log μijk = λ + λi. X + λj. Y + λk. Z + λij. XY + λik. XZ + λjk. YZ + λijk. XYZ • Interpretation: – Each pair of variables may be conditionally dependent – Odds ratios for any pair of variables may vary over levels of the third variable – perfect fit to observed data

Inference for Loglinear Models • Interpretation of Loglinear model parameters is at the level of the highestorder terms • χ2 or G 2 Goodness of Fit Tests can be used to select best fitting model • Parameter estimates are log odds ratios for associations

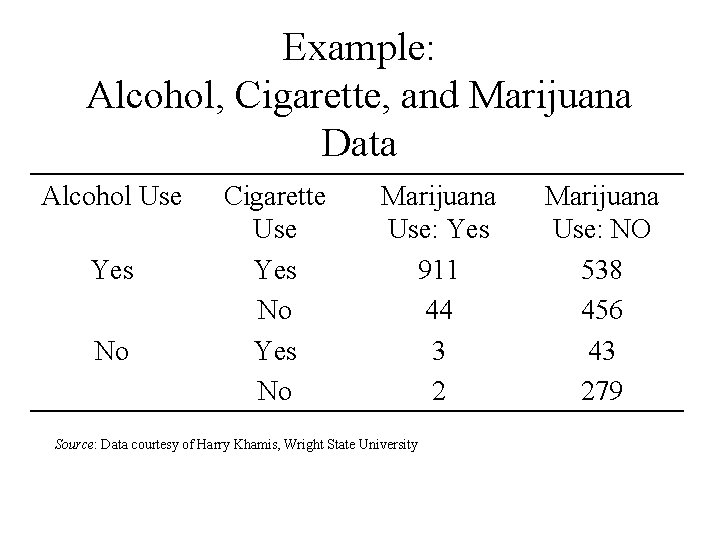
Example: Alcohol, Cigarette, and Marijuana Data Alcohol Use Yes No Cigarette Use Yes No Marijuana Use: Yes 911 44 3 2 Source: Data courtesy of Harry Khamis, Wright State University Marijuana Use: NO 538 456 43 279

SAS Code • • • data drugs; input a c m count; cards; 1 1 1 911 1 1 2 538 1 2 1 44 1 2 2 456 2 1 1 3 2 1 2 43 2 2 1 2 2 279 ; proc genmod; class a c m; model count = a c m / dist=poi link=log obstats; run; • • • • proc genmod; class a c m; model count = a c m c*m / dist=poi link=log obstats; run; proc genmod; class a c m; model count = a c m a*c a*m / dist=poi link=log obstats; run; proc genmod; class a c m; model count = a c m a*c c*m / dist=poi link=log obstats; run; proc genmod; class a c m; model count = a c m a*c a*m c*m a*c*m/ dist=poi link=log obstats; run; •

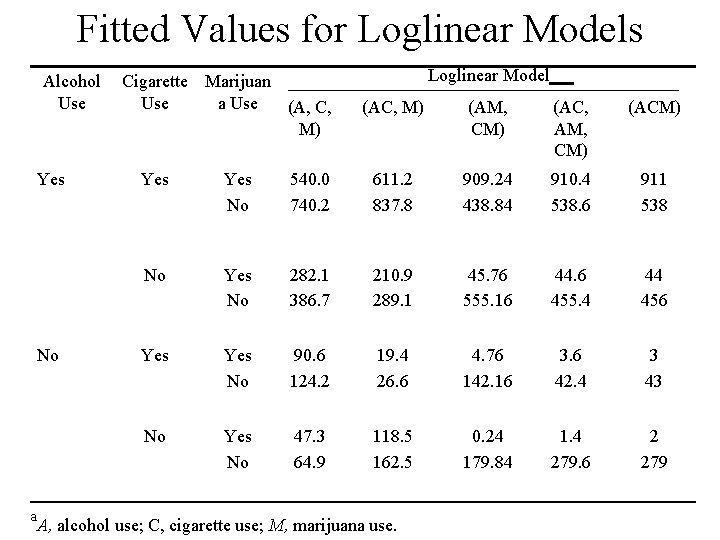
Fitted Values for Loglinear Models Alcohol Use Yes No a Cigarette Marijuan Use a Use (A, C, M) Loglinear Model (AC, M) (AM, CM) (AC, AM, CM) (ACM) Yes No 540. 0 740. 2 611. 2 837. 8 909. 24 438. 84 910. 4 538. 6 911 538 No Yes No 282. 1 386. 7 210. 9 289. 1 45. 76 555. 16 44. 6 455. 4 44 456 Yes No 90. 6 124. 2 19. 4 26. 6 4. 76 142. 16 3. 6 42. 4 3 43 No Yes No 47. 3 64. 9 118. 5 162. 5 0. 24 179. 84 1. 4 279. 6 2 279 A, alcohol use; C, cigarette use; M, marijuana use.

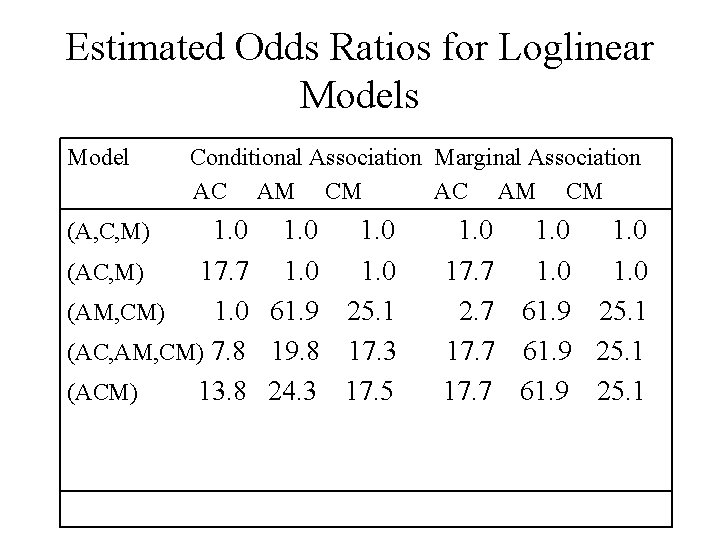
Estimated Odds Ratios for Loglinear Models Model Conditional Association Marginal Association AC AM CM 1. 0 (AC, M) 17. 7 1. 0 (AM, CM) 1. 0 61. 9 25. 1 (AC, AM, CM) 7. 8 19. 8 17. 3 (ACM) 13. 8 24. 3 17. 5 (A, C, M) 1. 0 17. 7 1. 0 2. 7 61. 9 25. 1 17. 7 61. 9 25. 1

Computation of the Odds Ratio

• Model (AC, AM, CM) permits all pairwise associations but maintains homogeneous odds rations between two variables at each level of the third. • The previous table shows that estimated odds ratios are very dependent on the model, and from this we can only say that the model fits well.

Conditional independence has implications regarding marginal (in) dependence; however, marginal (in) dependence does not have implications regarding conditional (in) dependence. Conditional independence->marginal independence Conditional independence->marginal dependence Marginal independence does not ->conditional independence Marginal dependence does not ->conditional dependence.