LOGIKA Logika je grka re koja oznaava uenje

LOGIKA • Logika je grčka reč koja označava učenje o govoru , razumevanju, razlozima i sl • • Logika je veština i metoda pravilnog mišljenja. Utvrđuje opšta pravila na osnovu kojih dolazimo do istine. • Primeri mišljenja: Devojke su lepše od dečaka Dečaci su pametniji od devojaka Ako neko puno radi, biće bogat. Ivan puno radi. Znači, Ivan je bogat. • Sposobnost da se logično misli je važno za svaku profesiju. • Logika kao nauka o zaključivanju koristi se u najrazličitijim oblastima nauke, a pogotovo u matematici. • Učeći matematiku sposobnost logičnog razmišljanja se povećava, a znanje matematike pomaže u rešavanju najrazličitijih ne matematičkih problema.

LOGIKA • • • Nastala je u 4 veku p. n. e. Stari Grci su pokušavali da proniknu u logiku matematičkih dokaza Treba spomenuti sledeća imena: Tales, Pitagora, Parmenid, Zenon, Sokrat, Platon…. • • Osnivač formalne logike je grčki filozof Aristotel (384 -322 p. n. e. ). Rođen u Stagiri, grčkoj koloniji na makedonskom poluostrvu. Od 18. do 37. godine pohađa Akademiju kao Platonov učenik. Na poziv kralja Filipa Makedonskog postaje tutor Aleksandra Velikog, koji je tada imao 13 godina. Prvi je podrobno obradio zakone logike i pravila zaključivanja u delu Organon, što u prevodu znači oruđe. U ovom delu sačinio je prvi skup pravila deduktivnog zaključivanja. • •

• Glavna mu je teza bila da se svako rasuđivenje može svesti na primenu konačno mnogo određenih pravila koja ne zavise od prirode objekta koji se proučava • U 17. i 18. veku Aristotelova formalna logika smatrala se obaveznim delom svakog obrazovanja • Kant (kraj 19. veka): “Sve što je bitno u logici, sve što se može reći o zakonima logike, rekao je Aristotel, pa je zbog toga formalna logika u nekom smislu mrtva nauka • Aristotelov autoritet u logici je bio toliko neprikosnoven, da je to smetalo razvitku logike

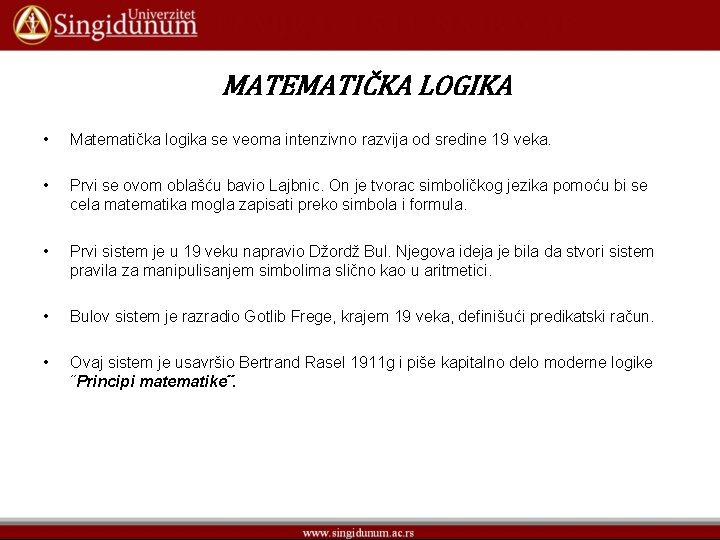
MATEMATIČKA LOGIKA • Matematička logika se veoma intenzivno razvija od sredine 19 veka. • Prvi se ovom oblašću bavio Lajbnic. On je tvorac simboličkog jezika pomoću bi se cela matematika mogla zapisati preko simbola i formula. • Prvi sistem je u 19 veku napravio Džordž Bul. Njegova ideja je bila da stvori sistem pravila za manipulisanjem simbolima slično kao u aritmetici. • Bulov sistem je razradio Gotlib Frege, krajem 19 veka, definišući predikatski račun. • Ovaj sistem je usavršio Bertrand Rasel 1911 g i piše kapitalno delo moderne logike ˝Principi matematike˝.

MATEMATIČKA LOGIKA • • • Matematička logika nije primena logike u matematici. To je matematička disciplina ( formalni sistem, a ne filozofija) koja je uvela strogost u definisanje pojmova. Obezbeđuje teorijske osnove mnogih matematičkih disciplina, a pre svega računarskih nauka. Omogućila je nastanak i razvoj digitalnih elektronskih računara. • • • Matematička logika u sebi sadrži sledeće oblasti: Teoriju skupova Teoriju dokaza Teoriju modela Teoriju rekurzija • Deli se na iskaznu logiku i predikatsku logiku •

ISKAZNA LOGIKA • • Polazni pojam u matematičkoj logici je iskaz. To afirmativna rečenica koja ima smisla i koja je ili tačna ili netačna • Iskaz ili sud je rečenica koja ima istinitosnu vrednost. • Iskazi se obeležavaju malim slovima p, q, r, …. . i nazivaju se iskazna slova • Istinitosna vrednost iskaza je

q Primeri

OSNOVNE LOGIČKE OPERACIJE • U svakodnevnom jeziku, rečenice se kombinuju u složene rečenice, korišenjem veznika i, ili, ne, ako onda i mnogih drugih. • • Istinitosna vrednost složene rečenice uslovljena je istinitošću njenih delova. Ove reči su u vezi sa logičkim operacijama. • Primer: p: Danas pada kiša q: Danas je novembar. Složena rečenica glasi Danas pada kiša i danas je novembar • Sastoji se od 2 dela spojenih veznikom i. Ova rečenica se može napisati kao p i q.

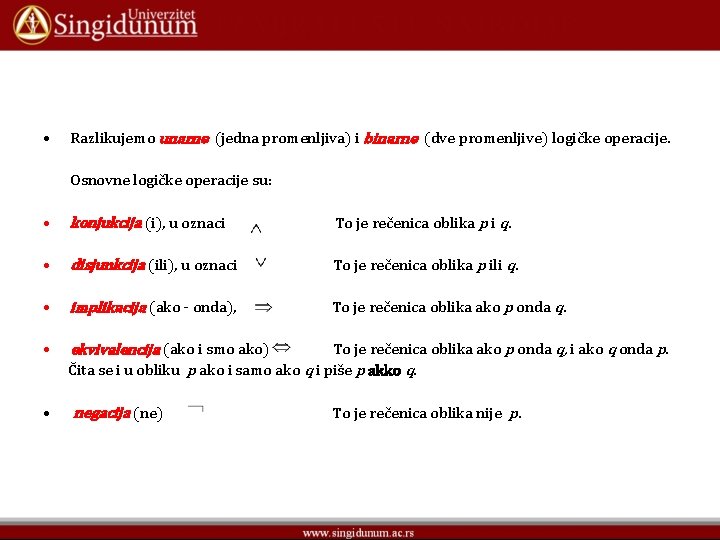
• Razlikujemo unarne (jedna promenljiva) i binarne (dve promenljive) logičke operacije. Osnovne logičke operacije su: • konjukcija (i), u oznaci To je rečenica oblika p i q. • disjunkcija (ili), u oznaci To je rečenica oblika p ili q. • implikacija (ako - onda), To je rečenica oblika ako p onda q. • ekvivalencija (ako i smo ako) To je rečenica oblika ako p onda q, i ako q onda p. Čita se i u obliku p ako i samo ako q i piše p akko q. • negacija (ne) To je rečenica oblika nije p.

. Istinitosna vrednost logičkih operacija data je sledećom tablicom.

• • • Istinitosna vrednost u tablici je u saglasnosti sa svakodnevnom logikom. Jedino kod implikacije naizgled nelogičnost vidimo u slučaju kada je Znači, impikacija je tačna bez obzira na vrednost iskaznog slova q. • Primer 1 : Ako je Srbija najveća na svetu, veća je od Crne Gore. Složena rečenica je tačna, jer ako je Srbija najveća na svetu, veća je od Crne Gore koja je manja od nje. • Primer 2 : Ako je Srbija najveća na svetu, veća je od SAD. Složena rečenica je tačna, jer ako je Srbija najveća na svetu, veća je od svake druge države .

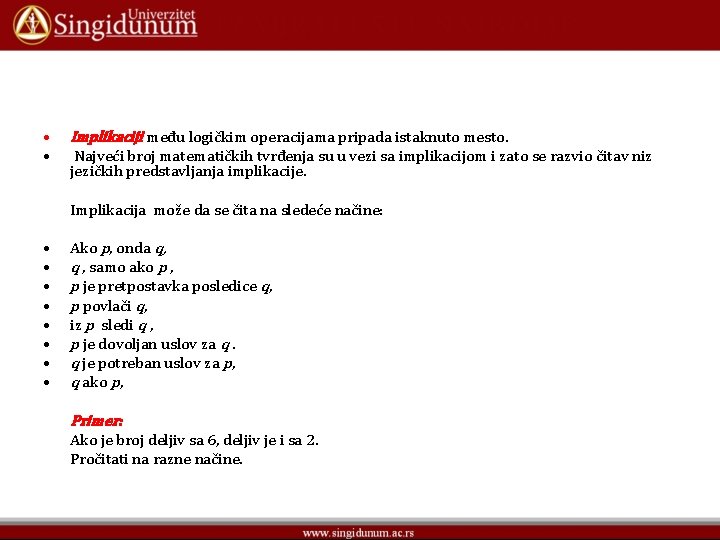
• • Implikaciji među logičkim operacijama pripada istaknuto mesto. Najveći broj matematičkih tvrđenja su u vezi sa implikacijom i zato se razvio čitav niz jezičkih predstavljanja implikacije. Implikacija može da se čita na sledeće načine: • • Ako p, onda q, q , samo ako p , p je pretpostavka posledice q, p povlači q, iz p sledi q , p je dovoljan uslov za q. q je potreban uslov za p, q ako p, Primer: Ako je broj deljiv sa 6, deljiv je i sa 2. Pročitati na razne načine.

Za implikaciju vezane su 3 dodatne vrste iskaza: • konverzija • inverzija • kontrapozicija • Primer: Ako je ona glumica, onda je ona popularna. -implikacija • Ako je ona popularna, onda je ona glumica. - konverzija • Ako je ona nije glumica, onda je ona nije popularna. - inverzija • Ako je ona nije popularna, onda je ona nije glumica. - kontrapozicija

• Ekvivalencija je dvostruka implikacija, odnosno Ekvivalencija se čita na sledeće načine: • • Ako p, onda q i obrnuto, p ako i samo ako q, p je potrebno i dovoljno da je q , p je potreban i dovoljan uslov za q. Reči ako i samo ako pišemo često u sledećem obliku akko. • Primer: Trougao je pravougli, ako i samo ako, je zbir kvadrata nad katetama jednak kvadratu nad hipotenuzom. • Primer: Broj je deljiv sa 6, akko je deljiv sa 2 i sa 3.

ISKAZNE FORMULE • Kombinovanjem iskaznih slova i znakova za logičke operacije dobijamo složene formule. • • • Definicija: • Primer: Iskazna slova čine iskaznu formulu. Iskaznu formulu čine i iskazna slova p, q , r i znaci za osnovne logičke operacije. Formule su: Istinitosnu vrednost iskazne formule moguće je odrediti istinitosnom tablicom.

• Prilikom pisanja iskaznih formula, ako se izostave zagrade, važno je znati prioritet logičkih operacija, koji možemo videti iz sledeće tablice. logički operator prioritet 1 2 3

• Primer: Odrediti istinitosnu tabicu formule T T T T

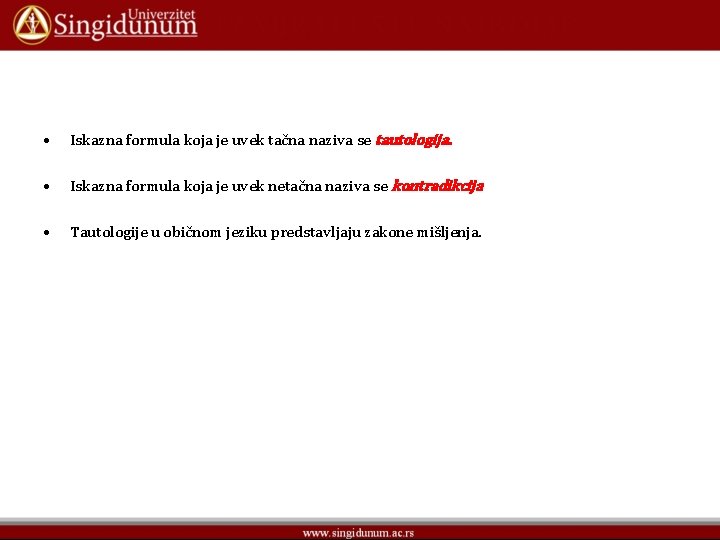
• Iskazna formula koja je uvek tačna naziva se tautologija. • Iskazna formula koja je uvek netačna naziva se kontradikcija • Tautologije u običnom jeziku predstavljaju zakone mišljenja.

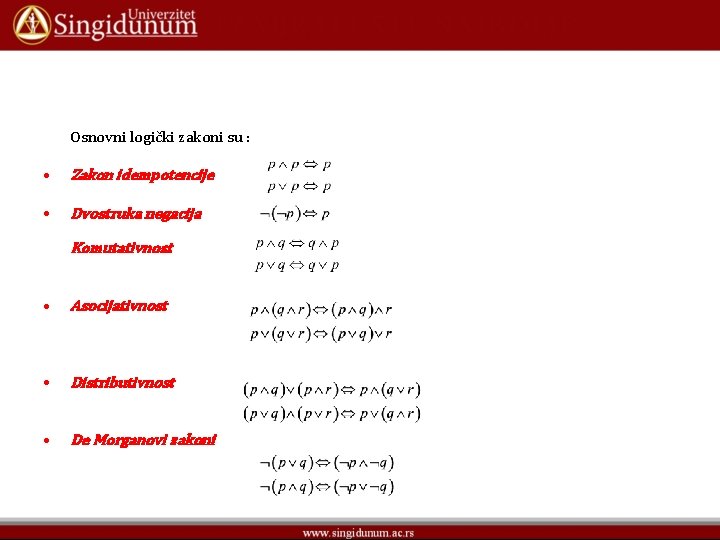
Osnovni logički zakoni su : • Zakon idempotencije • Dvostruka negacija Komutativnost • Asocijativnost • Distributivnost • De Morganovi zakoni

KVANTORI • • • Kvantori ili kvantifikatori u jeziku su reči svaki i neki. Osim ovih reči koriste se i drugi njihovi jezički oblici. Tako reč svaki u matematici znači isto što i bilo koji, ma koji, svi i slično, umesto reči neki koristi se i postoji, bar jedan, najmanje jedan i slično. • Univerzalni kvantor znači svaki i obeležava se sa - za svaki x važi a(x) • Egzistencijalni kvantor znači neki i obeležava se sa - postoji x za koje važi

• Višestruke primene kvantora • Kao što se iz ovih definicija može videti kvantori na neki način predstavljaju uopštenja logičkih operacija konjukcije odnosno disjunkcije. Prilikom zapisivanja različitih sadržaja upotrebom kvantora treba znati: • • Rečenica, svaki A je B, znači isto što i: Za svaki x, ako x ima osobinu A, onda x ima i osobinu B. Rečenica, neki A je B, znači isto što i: Postoji x, koji ima osobinu A i osobinu B.

Primer: Primenom kvantora napisati sledeće rečenice: • a) Svaki prirodni broj je pozitivan. • b) Postoji x takvo da je manje od 7. • c) Postoji tačno jedan broj čiji je kvadrat nula. • • Primer: Uporebom kvantora zapisati sledeće rečenice: a) x je oblika 2 k, gde je k ceo broj • b)Za svaki ceo broj x, postoji ceo broj y, takav da im je zbir 0.

• Negacija kvantora: • Primer: Negirati sledeće rečenice: • a) Svi prirodni brojevi su i celi brojevi. Negacija glasi: Neki prirodni brojevo nisu celi brojevi. • b) Neki prirodni brojevi su deljivi sa 5 Negacija glasi: Svi prirodni brojevi nisu deljivi sa 5.

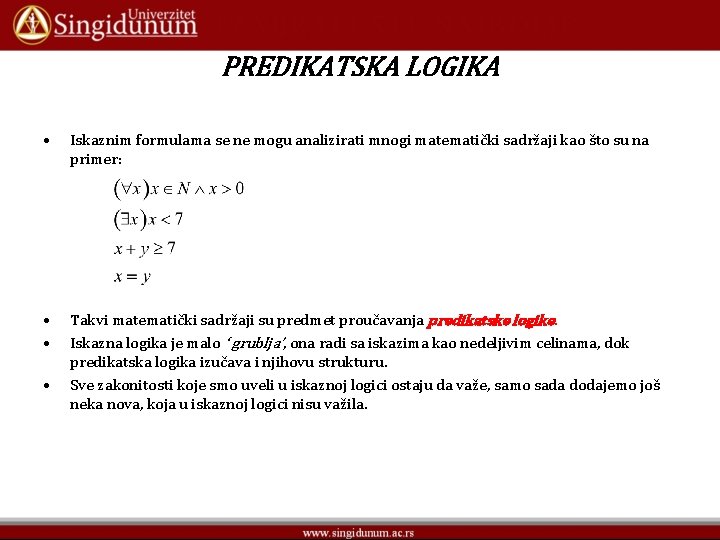
PREDIKATSKA LOGIKA • Iskaznim formulama se ne mogu analizirati mnogi matematički sadržaji kao što su na primer: • • Takvi matematički sadržaji su predmet proučavanja predikatske logike. Iskazna logika je malo ‘ grublja’, ona radi sa iskazima kao nedeljivim celinama, dok predikatska logika izučava i njihovu strukturu. Sve zakonitosti koje smo uveli u iskaznoj logici ostaju da važe, samo sada dodajemo još neka nova, koja u iskaznoj logici nisu važila. •

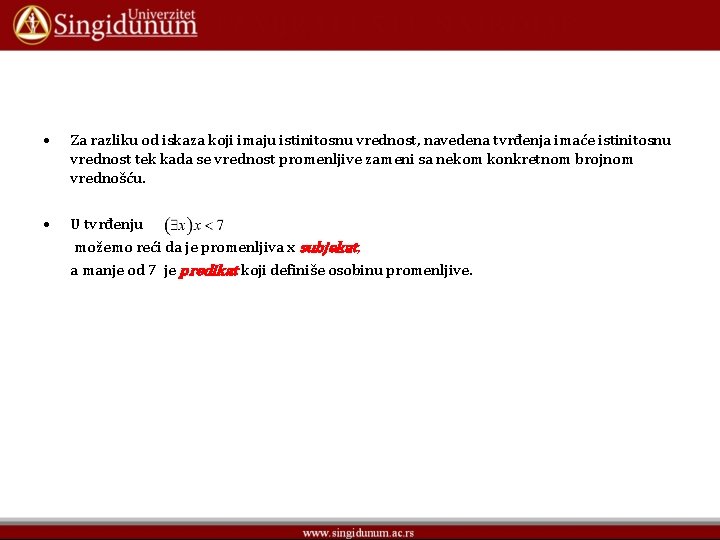
• Za razliku od iskaza koji imaju istinitosnu vrednost, navedena tvrđenja imaće istinitosnu vrednost tek kada se vrednost promenljive zameni sa nekom konkretnom brojnom vrednošću. • U tvrđenju možemo reći da je promenljiva x subjekat, a manje od 7 je predikat koji definiše osobinu promenljive.

• • • Takva tvrđenje možemo da zapišemo u obliku P(x) , gde x označava promenljivu, a P predikat. Predikatske formule grade se pomoću: Skupa konstanti Skupa promenljivih Operacijskih znakova Relacijskih znakova Simbola logičkih operacija Kvantora Pomoćnih simbola Korišćenjem ovih simbola mogu se opisati gotovo svi iskazi koji se u matematici pojavljuju, odnosno problemi koji se rešavaju pomoću računara. Predikatske formule se uvek definišu u odnosu na neki jezik, odnosno algebarsku strukturu. U okviru te strukture se vrši interpretacija formule. Znači, promenljive u formuli mogu da uzimaju različite vrednosti. Tek u konkretnoj interpretaciji možemo govoriti da li je neka predikatska formula tačna ili ne.

• Primer: Data je formula • Ona može da ima više interpretacija. • Jedna njena interpretacija u skupu N i relacija < kao vrednost znaka a bi bila • Za konkretne brojne vrednosti x, y, z nastaju različiti iskazi o prirodnim brojevima, koji su nekada tačni, a nekada ne. • Druga interpretacija je u skupu pravih, a relacija a je paralelno.

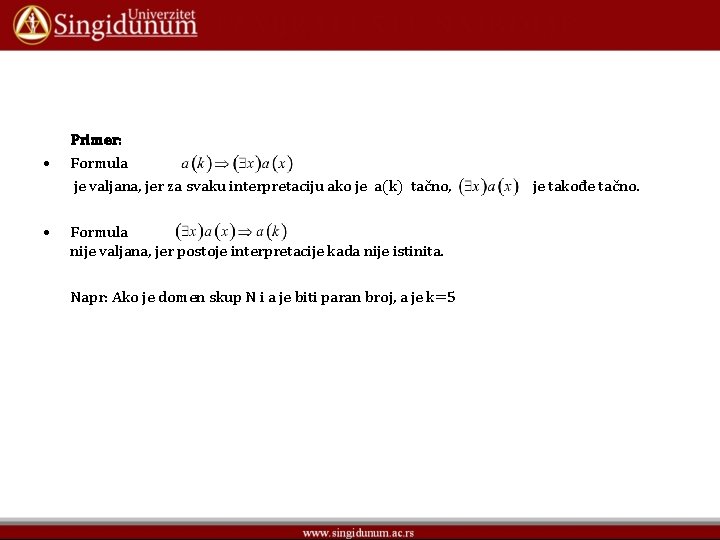
• • Primer: Formula je valjana, jer za svaku interpretaciju ako je a(k) tačno, Formula nije valjana, jer postoje interpretacije kada nije istinita. Napr: Ako je domen skup N i a je biti paran broj, a je k=5 je takođe tačno.

VALJANE FORMULE • Valjana formula u predikatskoj logici su manje više kao tautologija u iskaznoj logici. • Međutim, dok za ispitivanje da li je neka iskazna formula tautologija imamo jasno definisan postupak, za ispitivanje da li je neka predikatska formula valjana, jasnog i definisanog postupka nema. Valjanim formulama, isto kao i tautologijama ispituju se zakoni mišljenja. Predikatska formula je valjana, u oznaci ukoliko je istinita pri svakoj glavnoj interpretaciji. • •