LESSON 5 3 Solving Trigonometric Identities FiveMinute Check

LESSON 5– 3 Solving Trigonometric Identities

Five-Minute Check (over Lesson 5 -2) TEKS Then/Now Example 1: Solve by Isolating Trigonometric Expressions Example 2: Solve by Taking the Square Root of Each Side Example 3: Solve by Factoring Example 4: Real-World Example: Trigonometric Functions of Multiple Angles Example 5: Solve by Rewriting Using a Single Trigonometric Function Example 6: Solve by Squaring

Over Lesson 5 -2 Verify the identity sin x tan x = sec x – cos x. A. B. C. D.

Over Lesson 5 -2 Verify the identity 1 = tan x cos x csc x. A. B. C. D.

Over Lesson 5 -2 Verify the identity sec x – sec x sin 2 x = cos x. A. B. C. D.

Over Lesson 5 -2 Which of the following is equivalent to A. cos θ B. sec θ C. sin θ D. csc θ ?

Targeted TEKS P. 5(N) Generate and solve trigonometric equations in mathematical and real-world problems. Mathematical Processes P. 1(B), P. 1(G)

You verified trigonometric identities. (Lesson 5 -2) • Solve trigonometric equations using algebraic techniques. • Solve trigonometric equations using basic identities.

Solve by Isolating Trigonometric Expressions Solve . Original equation Subtract 3 cos x from each side to isolate the trigonometric expression. Solve for cos x.

Solve by Isolating Trigonometric Expressions The period of cosine is 2π, so you only need to find solutions on the interval [0, 2π). The solutions on this interval are –∞, . The solutions on the interval ( ∞) are then found by adding integer multiples 2π. Therefore, the general form of the solutions is x= Answer: , where n is an integer.

Solve sin x + A. B. C. D. = – sin x.

Solve by Taking the Square Root of Each Side Solve 3 tan 2 x – 4 = – 3 3 tan 2 x = 1 Original equation Add 4 to each side. Divide each side by 3. Take the square root of each side. Rationalize the denominator.

Solve by Taking the Square Root of Each Side The period of tangent is π. On the interval [0, π), tan x = when x = and tan x = when x = The solutions on the interval (–∞, ∞) have the general form Answer: , where n is an integer. .

Solve 5 tan 2 x – 15 = 0. A. B. C. D.

Solve by Factoring A. Find all solutions of interval [0, 2π). on the Original equation Isolate the trigonometric terms. Factor. Zero Product Property

Solve by Factoring Solve for cos x. Solve for x on [0, 2π). On the interval [0, 2π), the equation has solutions Answer: .

Solve by Factoring B. Find all solutions of 2 sin 2 x + sinx – 1 = 0 on the interval [0, 2π). Original equation Factor. Zero Product Property Solve for sin x. Solve for x on [0, 2π).

Solve by Factoring On the interval [0, 2π), the equation 2 sin 2 x + sinx – 1 = 0 has solutions Answer: .

Find all solutions of 2 tan 4 x – tan 2 x – 15 = 0 on the interval [0, π). A. B. C. D.

Trigonometric Functions of Multiple Angles PROJECTILES A projectile is sent off with an initial speed vo of 350 m/s and clears a fence 3000 m away. The height of the fence is the same height as the initial height of the projectile. If the distance the projectile traveled is given by , find the interval of possible launch angles to clear the fence.

Trigonometric Functions of Multiple Angles Original formula d = 3000 and v 0 = 350 Simplify. Multiply each side by 9. 8. Divide each side by 122, 500. Definition of inverse sine.

Trigonometric Functions of Multiple Angles Recall from Lesson 4 -6 that the range of the inverse sine function is restricted to acute angles of θ in the interval [– 90°, 90°]. Since we are finding the inverse sine of 2θ instead of θ, we need to consider angles in the interval [– 2(90°), 2(90°)] or [– 180°, 180°]. Use your calculator to find the acute angle and the reference angle relationship sin (180° − θ) = sin θ to find the obtuse angle. sin– 10. 24 = 2 13. 9° or 166. 1° = 2 7. 0° or 83. 1° = Definition of inverse sin– 1(0. 24) ≈13. 9° and sin(180° – 13. 9°) = 166. 1° Divide by 2.

Trigonometric Functions of Multiple Angles The interval is [7. 0°, 83. 1°]. The ball will clear the fence if the angle is between 7. 0° and 83. 1°. Answer: 7. 0° ≤ ≤ 83. 1° CHECK Substitute the angle measures into the original equation to confirm the solution. Original formula = 7. 0° or = 83. 1° Use a calculator.

GOLF A golf ball is sent off with an initial speed vo of 36 m/s and clears a small barricade 70 m away. The height of the barricade is the same height as the initial height of the ball. If the distance the ball traveled is given by , find the interval of possible launch angles to clear the barricade. A. 1. 6° ≤ ≤ 88. 5° C. 16. 0° ≤ ≤ 74. 0° B. 3. 1° ≤ ≤ 176. 9° D. 32° ≤ ≤ 148. 0°

Solve by Rewriting Using a Single Trigonometric Function Find all solutions of sin 2 x – sin x + 1 = cos 2 x on the interval [0, 2π). sin 2 x – sin x + 1 = cos 2 x Original equation –cos 2 x + sin 2 x – sin x + 1 = 0 –(1 – sin 2 x) + sin 2 x – sin x + 1 = 0 2 sin 2 x – sin x = 0 sin x (2 sin x – 1) = 0 Subtract cos 2 x from each side. Pythagorean Identity Simplify. Factor.

Solve by Rewriting Using a Single Trigonometric Function sin x = 0, π 2 sin x – 1 = 0 Zero Product Property 2 sin x = 1 Solve for sin x. Solve for x on [0, 2π).

Solve by Rewriting Using a Single Trigonometric Function Answer: CHECK The graphs of Y 1 = sin 2 x – sin x + 1 and Y 2 = cos 2 x intersect at [0, 2π) as shown. on the interval

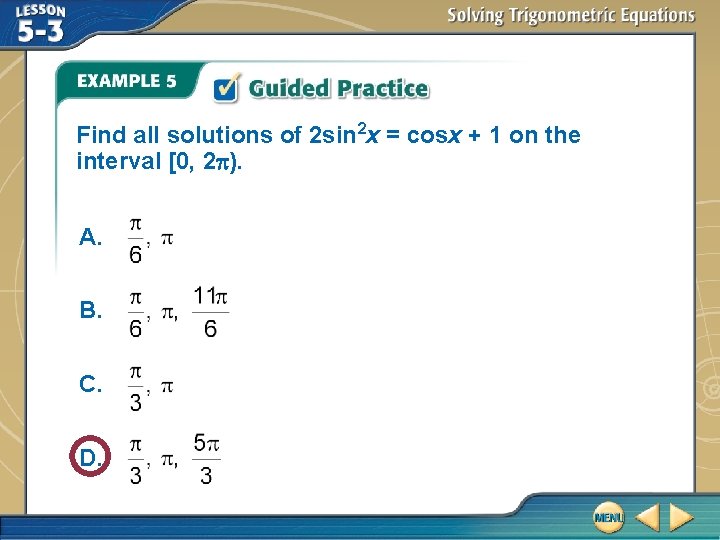
Find all solutions of 2 sin 2 x = cosx + 1 on the interval [0, 2 ). A. B. C. D.

Solve by Squaring Find all solutions of sin x – cos x = 1 on the interval [0, 2π). sin x – cos x = 1 sin x = cos x + 1 Original equation Add cos x to each side. sin 2 x = cos 2 x + 2 cos x + 1 Square each side. 1 – cos 2 x = cos 2 x + 2 cos x + 1 Pythagorean Identity 0 = 2 cos 2 x + 2 cos x Subtract 1 – cos 2 x from each side. 0 = cos 2 x + cos x Divide each side by 2. 0 = cos x(cos x + 1) Factor.

Solve by Squaring cos x = 0 cos x + 1 = 0 cos x = – 1 , x=π Zero Product Property Solve for cos x. Solve for x on [0, 2). Original formula Substitute Simplify. sin π – cos π = 1

Solve by Squaring Therefore, the only valid solutions are interval. Answer: on the

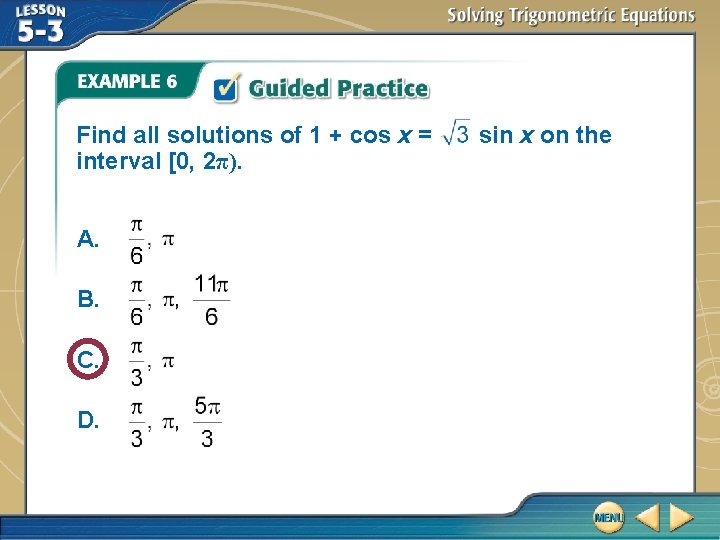
Find all solutions of 1 + cos x = interval [0, 2π). A. B. C. D. sin x on the

LESSON 5– 3 Solving Trigonometric Identities